Navigation

Field \QQ of Rational Numbers.

The class RationalField represents the field \QQ of (arbitrary precision) rational numbers. Each rational number is an instance of the class Rational.

Interactively, an instance of RationalField is available as QQ.

sage: QQ
Rational Field

Values of various types can be converted to rational numbers by using the __call__ method of RationalField (that is, by treating QQ as a function).

sage: RealField(9).pi()
3.1
sage: QQ(RealField(9).pi())
22/7
sage: QQ(RealField().pi())
245850922/78256779
sage: QQ(35)
35
sage: QQ('12/347')
12/347
sage: QQ(exp(pi*I))
-1
sage: x = polygen(ZZ)
sage: QQ((3*x)/(4*x))
3/4

TEST:

sage: Q = RationalField()
sage: Q == loads(dumps(Q))
True
sage: RationalField() is RationalField()
True
class sage.rings.rational_field.RationalField

Bases: sage.rings.rational_field._uniq, sage.rings.number_field.number_field_base.NumberField

The class RationalField represents the field \QQ of rational numbers.

EXAMPLES:

sage: a = long(901824309821093821093812093810928309183091832091)
sage: b = QQ(a); b
901824309821093821093812093810928309183091832091
sage: QQ(b)
901824309821093821093812093810928309183091832091
sage: QQ(int(93820984323))
93820984323
sage: QQ(ZZ(901824309821093821093812093810928309183091832091))
901824309821093821093812093810928309183091832091
sage: QQ('-930482/9320842317')
-930482/9320842317
sage: QQ((-930482, 9320842317))
-930482/9320842317
sage: QQ([9320842317])
9320842317
sage: QQ(pari(39029384023840928309482842098430284398243982394))
39029384023840928309482842098430284398243982394
sage: QQ('sage')
...
TypeError: unable to convert sage to a rational

Coercion from the reals to the rational is done by default using continued fractions.

sage: QQ(RR(3929329/32))
3929329/32
sage: QQ(-RR(3929329/32))
-3929329/32
sage: QQ(RR(1/7)) - 1/7
0

If you specify an optional second base argument, then the string representation of the float is used.

sage: QQ(23.2, 2)
6530219459687219/281474976710656
sage: 6530219459687219.0/281474976710656
23.20000000000000
sage: a = 23.2; a
23.2000000000000
sage: QQ(a, 10)
116/5

Here’s a nice example involving elliptic curves:

sage: E = EllipticCurve('11a')
sage: L = E.lseries().at1(300)[0]; L
0.253841860855911
sage: O = E.period_lattice().omega(); O
1.26920930427955
sage: t = L/O; t
0.200000000000000
sage: QQ(RealField(45)(t))
1/5
absolute_degree()

EXAMPLES:

sage: QQ.absolute_degree()
1
algebraic_closure()

Return the algebraic closure of self (which is QQbar).

EXAMPLES:

sage: QQ.algebraic_closure()
Algebraic Field
characteristic()

Return 0, since the rational field has characteristic 0.

EXAMPLES:

sage: c = QQ.characteristic(); c
0
sage: parent(c)
Integer Ring
class_number()

Return the class number of the field of rational numbers, which is 1.

EXAMPLES:

sage: QQ.class_number()
1
completion(p, prec, extras={})
complex_embedding(prec=53)

Return embedding of the rational numbers into the complex numbers.

EXAMPLES:

sage: QQ.complex_embedding()
Ring morphism:
  From: Rational Field
  To:   Complex Field with 53 bits of precision
  Defn: 1 |--> 1.00000000000000
sage: QQ.complex_embedding(20)
Ring morphism:
  From: Rational Field
  To:   Complex Field with 20 bits of precision
  Defn: 1 |--> 1.0000
construction()
degree()

EXAMPLES:

sage: QQ.degree()
1
discriminant()

Return the discriminant of the field of rational numbers, which is 1.

EXAMPLES:

sage: QQ.discriminant()
1
embeddings(K)

Return list of the one embedding of \QQ into K, if it exists.

EXAMPLES:

sage: QQ.embeddings(QQ)
[Ring Coercion endomorphism of Rational Field]
sage: QQ.embeddings(CyclotomicField(5))
[Ring Coercion morphism:
  From: Rational Field
  To:   Cyclotomic Field of order 5 and degree 4]

K must have characteristic 0:

sage: QQ.embeddings(GF(3))
...
ValueError: no embeddings of the rational field into K.
extension(poly, names, check=True, embedding=None)

EXAMPLES:

We make a single absolute extension:

sage: K.<a> = QQ.extension(x^3 + 5); K
Number Field in a with defining polynomial x^3 + 5

We make an extension generated by roots of two polynomials:

sage: K.<a,b> = QQ.extension([x^3 + 5, x^2 + 3]); K
Number Field in a with defining polynomial x^3 + 5 over its base field
sage: b^2
-3
sage: a^3
-5
gen(n=0)

EXAMPLES:

sage: QQ.gen()
1
gens()

EXAMPLES:

sage: QQ.gens()
(1,)
is_absolute()

\QQ is an absolute extension of \QQ.

EXAMPLES:

sage: QQ.is_absolute()
True
is_atomic_repr()
is_field(proof=True)

Return True, since the rational field is a field.

EXAMPLES:

sage: QQ.is_field()
True
is_finite()

Return False, since the rational field is not finite.

EXAMPLES:

sage: QQ.is_finite()
False
is_prime_field()

Return True, since \QQ is a prime field.

EXAMPLES:

sage: QQ.is_prime_field()
True
is_subring(K)

Return True if \QQ is a subring of K.

We are only able to determine this in some cases, e.g., when K is a field or of positive characteristic.

EXAMPLES:

sage: QQ.is_subring(QQ)
True
sage: QQ.is_subring(QQ['x'])
True
sage: QQ.is_subring(GF(7))
False
sage: QQ.is_subring(CyclotomicField(7))
True
sage: QQ.is_subring(ZZ)
False
sage: QQ.is_subring(Frac(ZZ))
True
maximal_order()

Return the maximal order of the rational numbers, i.e., the ring \ZZ of integers.

EXAMPLES:

sage: QQ.maximal_order()
Integer Ring
sage: QQ.ring_of_integers ()
Integer Ring
ngens()

EXAMPLES:

sage: QQ.ngens()
1
number_field()

Return the number field associated to \QQ. Since \QQ is a number field, this just returns \QQ again.

EXAMPLES:

sage: QQ.number_field() is QQ
True
order()

EXAMPLES:

sage: QQ.order()
+Infinity
power_basis()

Return a power basis for this number field over its base field.

The power basis is always [1] for the rational field. This method is defined to make the rational field behave more like a number field.

EXAMPLES:

sage: QQ.power_basis()
[1]
random_element(num_bound=None, den_bound=None, distribution=None)

EXAMPLES:

sage: QQ.random_element(10,10) # random output
-5/3
range_by_height(start, end=None)

Range function for rational numbers, ordered by height.

Returns a Python generator for the list of rational numbers with heights in range(start, end). Follows the same convention as Python range, see range? for details.

See also QQ.__iter__?

EXAMPLES:

All rational numbers with height strictly less than 4:

sage: list(QQ.range_by_height(4))
[0, 1, -1, 1/2, -1/2, 2, -2, 1/3, -1/3, 3, -3, 2/3, -2/3, 3/2, -3/2]
sage: [a.height() for a in QQ.range_by_height(4)]
[1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3]

All rational numbers with height 2:

sage: list(QQ.range_by_height(2, 3))
[1/2, -1/2, 2, -2]

Nonsensical integer arguments will return an empty generator:

sage: list(QQ.range_by_height(3, 3))
[]
sage: list(QQ.range_by_height(10, 1))
[]

There are no rational numbers with height 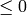\leq 0:

sage: list(QQ.range_by_height(-10, 1))
[]
signature()

Return the signature of the rational field, which is (1,0), since there are 1 real and no complex embeddings.

EXAMPLES:

sage: QQ.signature()
(1, 0)
zeta(n=2)

Return a root of unity in self.

INPUT:

  • n - integer (default: 2) order of the root of unity

EXAMPLES:

sage: QQ.zeta() 
-1
sage: QQ.zeta(2) 
-1
sage: QQ.zeta(1) 
1
sage: QQ.zeta(3) 
...
ValueError: no n-th root of unity in rational field
sage.rings.rational_field.frac(n, d)
sage.rings.rational_field.is_RationalField(x)

Previous topic

Elements of \ZZ/n\ZZ

Next topic

Rational Numbers

This Page

Navigation

© Copyright 2005--2010, The Sage Development Team. Created using Sphinx 0.6.3.