Sage supports arithmetic in finite prime and extension fields.
Several implementation for prime fields are implemented natively in
Sage for several sizes of primes  . These implementations
are
. These implementations
are
Small extension fields of cardinality 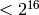 are
implemented using tables of Zech logs via the Givaro C++ library
(sage.rings.finite_rings.finite_field_givaro.FiniteField_givaro).
While this representation is very fast it is limited to finite
fields of small cardinality. Larger finite extension fields of
order
are
implemented using tables of Zech logs via the Givaro C++ library
(sage.rings.finite_rings.finite_field_givaro.FiniteField_givaro).
While this representation is very fast it is limited to finite
fields of small cardinality. Larger finite extension fields of
order 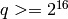 are internally represented as
polynomials over smaller finite prime fields. If the
characteristic of such a field is 2 then NTL is used internally to
represent the field
(sage.rings.finite_rings.element_ntl_gf2e.FiniteField_ntl_gf2e).
In all other case the PARI C library is used
(sage.rings.finite_rings.finite_field_ext_pari.FiniteField_ext_pari).
are internally represented as
polynomials over smaller finite prime fields. If the
characteristic of such a field is 2 then NTL is used internally to
represent the field
(sage.rings.finite_rings.element_ntl_gf2e.FiniteField_ntl_gf2e).
In all other case the PARI C library is used
(sage.rings.finite_rings.finite_field_ext_pari.FiniteField_ext_pari).
However, this distinction is internal only and the user usually does not have to worry about it because consistency across all implementations is aimed for. In all extension field implementations the user may either specify a minimal polynomial or leave the choice to Sage.
For small finite fields the default choice are Conway polynomials.
The Conway polynomial 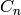 is the lexicographically first
monic irreducible, primitive polynomial of degree
is the lexicographically first
monic irreducible, primitive polynomial of degree  over
over
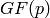 with the property that for a root
with the property that for a root 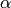 of
of 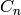 we have that
we have that
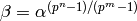 is a root of
is a root of
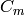 for all
for all 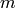 dividing
dividing  . Sage
contains a database of Conway polynomials which also can be queried
independently of finite field construction.
. Sage
contains a database of Conway polynomials which also can be queried
independently of finite field construction.
While Sage supports basic arithmetic in finite fields some more advanced features for computing with finite fields are still not implemented. For instance, Sage does not calculate embeddings of finite fields yet.
EXAMPLES:
sage: k = GF(5); type(k)
<class 'sage.rings.finite_rings.finite_field_prime_modn.FiniteField_prime_modn'>
sage: k = GF(5^2,'c'); type(k)
<class 'sage.rings.finite_rings.finite_field_givaro.FiniteField_givaro'>
sage: k = GF(2^16,'c'); type(k)
<type 'sage.rings.finite_rings.element_ntl_gf2e.FiniteField_ntl_gf2e'>
sage: k = GF(3^16,'c'); type(k)
<class 'sage.rings.finite_rings.finite_field_ext_pari.FiniteField_ext_pari'>
Finite Fields support iteration, starting with 0.
sage: k = GF(9, 'a')
sage: for i,x in enumerate(k): print i,x
0 0
1 2*a
2 a + 1
3 a + 2
4 2
5 a
6 2*a + 2
7 2*a + 1
8 1
sage: for a in GF(5):
... print a
0
1
2
3
4
We output the base rings of several finite fields.
sage: k = GF(3); type(k)
<class 'sage.rings.finite_rings.finite_field_prime_modn.FiniteField_prime_modn'>
sage: k.base_ring()
Finite Field of size 3
sage: k = GF(9,'alpha'); type(k)
<class 'sage.rings.finite_rings.finite_field_givaro.FiniteField_givaro'>
sage: k.base_ring()
Finite Field of size 3
sage: k = GF(3^40,'b'); type(k)
<class 'sage.rings.finite_rings.finite_field_ext_pari.FiniteField_ext_pari'>
sage: k.base_ring()
Finite Field of size 3
Further examples:
sage: GF(2).is_field()
True
sage: GF(next_prime(10^20)).is_field()
True
sage: GF(19^20,'a').is_field()
True
sage: GF(8,'a').is_field()
True
AUTHORS:
Bases: sage.structure.factory.UniqueFactory
Return the globally unique finite field of given order with generator labeled by the given name and possibly with given modulus.
INPUT:
order - int
name - string; must be specified if not a prime field
modulus - (optional) either a defining polynomial for the field, i.e., generator of the field will be a root of this polynomial; or a string:
- ‘conway’: force the use of a Conway polynomial, will raise a RuntimeError if none is found in the database;
- ‘random’: use a random irreducible polynomial;
- ‘default’: a Conway polynomial is used if found. Otherwise a sparse polynomial is used for binary fields and a random polynomial is used for other characteristics.
Other options might be available depending on the implementation.
elem_cache - cache all elements to avoid creation time (default: order < 500)
check_irreducible - verify that the polynomial modulus is irreducible
args - additional parameters passed to finite field implementations
kwds - additional keyword parameters passed to finite field implementations
ALIAS: You can also use GF instead of FiniteField - they are identical.
EXAMPLES:
sage: k.<a> = FiniteField(9); k
Finite Field in a of size 3^2
sage: parent(a)
Finite Field in a of size 3^2
sage: charpoly(a, 'y')
y^2 + 2*y + 2
sage: F.<x> = GF(5)[]
sage: K.<a> = GF(5**5, name='a', modulus=x^5 - x +1 )
sage: f = K.modulus(); f
x^5 + 4*x + 1
sage: type(f)
<type 'sage.rings.polynomial.polynomial_zmod_flint.Polynomial_zmod_flint'>
The modulus must be irreducible:
sage: K.<a> = GF(5**5, name='a', modulus=x^5 - x )
...
ValueError: finite field modulus must be irreducible but it is not
You can’t accidentally fool the constructor into thinking the modulus is irreducible when it isn’t mod p, since it actually tests irreducibility modulo p.
sage: F.<x> = QQ[]
sage: factor(x^5+2)
x^5 + 2
sage: K.<a> = GF(5**5, name='a', modulus=x^5 + 2 )
...
ValueError: finite field modulus must be irreducible but it is not
If you wish to live dangerously, you can tell the constructor not to test irreducibility using check_irreducible=False, but this can easily lead to crashes and hangs - so do not do it unless you know that the modulus really is irreducible!
sage: F.<x> = GF(5)[]
sage: K.<a> = GF(5**2, name='a', modulus=x^2 + 2, check_irreducible=False)
For example, you may print finite field elements as integers. This
currently only works if the order of field is 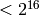 ,
though.
,
though.
sage: k.<a> = GF(2^8,repr='int')
sage: a
2
The order of a finite field must be a prime power:
sage: GF(100)
...
ValueError: the order of a finite field must be a prime power
Finite fields with random modulus are not cached:
sage: k.<a> = GF(2^17,modulus='random')
sage: n.<a> = GF(2^17,modulus='random')
sage: n is k
False
We check that various ways of creating the same finite field yield the same object.
sage: K = GF(7, 'a')
sage: L = GF(7, 'b')
sage: K is L
True
sage: K = GF(4,'a'); K.modulus()
x^2 + x + 1
sage: L = GF(4,'a', K.modulus())
sage: K is L
True
sage: M = GF(4,'a', K.modulus().change_variable_name('y'))
sage: K is M
True
EXAMPLES:
sage: GF.create_key_and_extra_args(9, 'a')
((9, ('a',), 'conway', None, '{}'), {})
sage: GF.create_key_and_extra_args(9, 'a', foo='value')
((9, ('a',), 'conway', None, "{'foo': 'value'}"), {'foo': 'value'})
EXAMPLES:
sage: K = GF(19)
sage: loads(dumps(K)) is K
True
EXAMPLES:
sage: key, extra = GF.create_key_and_extra_args(9, 'a'); key
(9, ('a',), 'conway', None, '{}')
sage: K = GF.create_object(0, key); K
Finite Field in a of size 3^2
sage: GF.other_keys(key, K)
[(9, ('a',), x^2 + 2*x + 2, None, '{}'),
(9, ('a',), x^2 + 2*x + 2, 'givaro', '{}')]
Return the Conway polynomial of degree n over GF(p), which is loaded from a table.
If the requested polynomial is not known, this function raises a RuntimeError exception.
INPUT:
OUTPUT:
Note
The first time this function is called a table is read from disk, which takes a fraction of a second. Subsequent calls do not require reloading the table.
See also the ConwayPolynomials() object, which is a
table of Conway polynomials. For example, if
c=ConwayPolynomials(), then
c.primes() is a list of all primes for which the
polynomials are known, and for a given prime  ,
c.degree(p) is a list of all degrees for which the
Conway polynomials are known.
,
c.degree(p) is a list of all degrees for which the
Conway polynomials are known.
EXAMPLES:
sage: conway_polynomial(2,5)
x^5 + x^2 + 1
sage: conway_polynomial(101,5)
x^5 + 2*x + 99
sage: conway_polynomial(97,101)
...
RuntimeError: requested conway polynomial not in database.
Return True if the Conway polynomial over 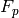 of degree
of degree
 is in the database and False otherwise.
is in the database and False otherwise.
If the Conway polynomial is in the database, to obtain it use the command conway_polynomial(p,n).
EXAMPLES:
sage: exists_conway_polynomial(2,3)
True
sage: exists_conway_polynomial(2,-1)
False
sage: exists_conway_polynomial(97,200)
False
sage: exists_conway_polynomial(6,6)
False
Returns True if x is a prime finite field.
EXAMPLES:
sage: from sage.rings.finite_rings.constructor import is_PrimeFiniteField
sage: is_PrimeFiniteField(QQ)
False
sage: is_PrimeFiniteField(GF(7))
True
sage: is_PrimeFiniteField(GF(7^2,'a'))
False
sage: is_PrimeFiniteField(GF(next_prime(10^90,proof=False)))
True