Univariate Polynomials over GF(2) via NTL’s GF2X.

AUTHOR: - Martin Albrecht (2008-10) initial implementation

class sage.rings.polynomial.polynomial_gf2x.Polynomial_GF2X

Bases: sage.rings.polynomial.polynomial_gf2x.Polynomial_template

Univariate Polynomials over GF(2) via NTL’s GF2X.

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x^3 + x^2 + 1
x^3 + x^2 + 1

is_irreducible()

Return True precisely if this polynomial is irreducible over GF(2).

EXAMPLES:

sage: R.<x> = GF(2)[]
sage: (x^2 + 1).is_irreducible()
False
sage: (x^3 + x + 1).is_irreducible()
True

modular_composition(g, h, algorithm=None)

Compute .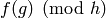

Both implementations use Brent-Kung’s Algorithm 2.1 (Fast Algorithms for Manipulation of Formal Power Series, JACM 1978).

INPUT:

• g – a polynomial
• h – a polynomial
• algorithm – either ‘native’ or ‘ntl’ (default: ‘native’)

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: r = 279
sage: f = x^r + x +1
sage: g = x^r
sage: g.modular_composition(g, f) == g(g) % f
True

sage: P.<x> = GF(2)[]
sage: f = x^29 + x^24 + x^22 + x^21 + x^20 + x^16 + x^15 + x^14 + x^10 + x^9 + x^8 + x^7 + x^6 + x^5 + x^2
sage: g = x^31 + x^30 + x^28 + x^26 + x^24 + x^21 + x^19 + x^18 + x^11 + x^10 + x^9 + x^8 + x^5 + x^2 + 1
sage: h = x^30 + x^28 + x^26 + x^25 + x^24 + x^22 + x^21 + x^18 + x^17 + x^15 + x^13 + x^12 + x^11 + x^10 + x^9 + x^4
sage: f.modular_composition(g,h) == f(g) % h
True

AUTHORS:

• Paul Zimmermann (2008-10) initial implementation
• Martin Albrecht (2008-10) performance improvements

class sage.rings.polynomial.polynomial_gf2x.Polynomial_template

Bases: sage.rings.polynomial.polynomial_element.Polynomial

Template for interfacing to external C / C++ libraries for implementations of polynomials.

AUTHORS:

• Robert Bradshaw (2008-10): original idea for templating
• Martin Albrecht (2008-10): initial implementation

This file implements a simple templating engine for linking univariate polynomials to their C/C++ library implementations. It requires a ‘linkage’ file which implements the celement_ functions (see sage.libs.ntl.ntl_GF2X_linkage for an example). Both parts are then plugged together by inclusion of the linkage file when inheriting from this class. See sage.rings.polynomial.polynomial_gf2x for an example.

We illustrate the generic glueing using univariate polynomials over .

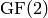Note

Implementations using this template MUST implement coercion from base ring elements and __getitem__. See Polynomial_GF2X for an example.

degree()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.degree()
1
sage: P(1).degree()
0
sage: P(0).degree()
-1

gcd(other)

Return the greatest common divisor of self and other.

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: f = x*(x+1)
sage: f.gcd(x+1)
x + 1
sage: f.gcd(x^2)
x

is_gen()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.is_gen()
True
sage: (x+1).is_gen()
False

is_one()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: P(1).is_one()
True

is_zero()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.is_zero()
False

list()

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: x.list()
[0, 1]
sage: list(x)
[0, 1]

quo_rem(right)

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: f = x^2 + x + 1
sage: f.quo_rem(x + 1)
(x, 1)

shift(n)

EXAMPLE:

sage: P.<x> = GF(2)[]
sage: f = x^3 + x^2 + 1
sage: f.shift(1)
x^4 + x^3 + x
sage: f.shift(-1)
x^2 + x

truncate(n)

Returns this polynomial mod .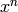

EXAMPLES:

sage: R.<x> =GF(2)[]
sage: f = sum(x^n for n in range(10)); f
x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1
sage: f.truncate(6)
x^5 + x^4 + x^3 + x^2 + x + 1

xgcd(other)

Computes extended gcd of self and other.

EXAMPLE:

sage: P.<x> = GF(7)[]
sage: f = x*(x+1)
sage: f.xgcd(x+1)
(x + 1, 0, 1)
sage: f.xgcd(x^2)
(x, 1, 6)

sage.rings.polynomial.polynomial_gf2x.make_element(parent, args)