Dense univariate polynomials over $\ZZ$ , implemented using FLINT.¶

AUTHORS:

David Harvey: rewrote to talk to NTL directly, instead of via ntl.pyx (2007-09); a lot of this was based on Joel Mohler’s recent rewrite of the NTL wrapper
David Harvey: split off from polynomial_element_generic.py (2007-09)
Burcin Erocal: rewrote to use FLINT (2008-06-16)

class sage.rings.polynomial.polynomial_integer_dense_flint.Polynomial_integer_dense_flint¶

Bases: sage.rings.polynomial.polynomial_element.Polynomial

A dense polynomial over the integers, implemented via FLINT.

content()¶

Return the greatest common divisor of the coefficients of this polynomial.

EXAMPLES:

sage: R.<x> = PolynomialRing(ZZ)
sage: (2*x^2 - 4*x^4 + 14*x^7).content()
2
sage: x.content()
1
sage: R(1).content()
1
sage: R(0).content()
0

TESTS:

sage: t = x^2+x+1
sage: t.content()
1
sage: (123456789123456789123456789123456789123456789*t).content()
123456789123456789123456789123456789123456789

degree(gen=None)¶

Return the degree of this polynomial. The zero polynomial has degree -1.

EXAMPLES:

sage: R.<x> = PolynomialRing(ZZ)
sage: x.degree()
1
sage: (x^2).degree()
2
sage: R(1).degree()
0
sage: R(0).degree()
-1

discriminant(proof=True)¶

Return the discriminant of self, which is by definition

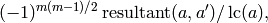
$(-1)^{m(m-1)/2} \mathop{\mathrm{resultant}}(a, a')/\mathop{\mathrm{lc}}(a),$

where 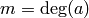$m = \mathop{\mathrm{deg}}(a)$ , and $\mathop{\mathrm{lc}}(a)$ is the leading coefficient of a. If proof is False (the default is True), then this function may use a randomized strategy that errors with probability no more than $2^{-80}$ .

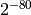EXAMPLES:

sage: R.<x> = ZZ[]
sage: f = 3*x^3 + 2*x + 1
sage: f.discriminant()
-339
sage: f.discriminant(proof=False)
-339

factor()¶

This function overrides the generic polynomial factorization to make a somewhat intelligent decision to use Pari or NTL based on some benchmarking.

Note: This function factors the content of the polynomial, which can take very long if it’s a really big integer. If you do not need the content factored, divide it out of your polynomial before calling this function.

EXAMPLES:

sage: R.<x>=ZZ[]
sage: f=x^4-1
sage: f.factor()
(x - 1) * (x + 1) * (x^2 + 1)
sage: f=1-x
sage: f.factor()
(-1) * (x - 1)
sage: f.factor().unit()
-1
sage: f = -30*x; f.factor()
(-1) * 2 * 3 * 5 * x

factor_mod(p)¶

Return the factorization of self modulo the prime $p$ .

INPUT:

p – prime

OUTPUT:

factorization of self reduced modulo p.

EXAMPLES:

sage: R.<x> = ZZ['x']
sage: f = -3*x*(x-2)*(x-9) + x
sage: f.factor_mod(3)
x
sage: f = -3*x*(x-2)*(x-9)
sage: f.factor_mod(3)
...
ValueError: factorization of 0 not defined

sage: f = 2*x*(x-2)*(x-9)
sage: f.factor_mod(7)
(2) * x * (x + 5)^2

factor_padic(p, prec=10)¶

Return $p$ -adic factorization of self to given precision.

INPUT:

p – prime
prec – integer; the precision

OUTPUT:

factorization of self reduced modulo p.

EXAMPLES:

sage: R.<x> = PolynomialRing(ZZ)
sage: f = x^2 + 1
sage: f.factor_padic(5, 4)
((1 + O(5^4))*x + (2 + 5 + 2*5^2 + 5^3 + O(5^4))) * ((1 + O(5^4))*x + (3 + 3*5 + 2*5^2 + 3*5^3 + O(5^4)))

gcd(right)¶

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

is_zero()¶

Returns True if self is equal to zero.

EXAMPLES:

sage: R.<x> = ZZ[]
sage: R(0).is_zero()
True
sage: R(1).is_zero()
False
sage: x.is_zero()
False

lcm(right)¶

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

list()¶

Return a new copy of the list of the underlying elements of self.

EXAMPLES:

sage: x = PolynomialRing(ZZ,'x').0
sage: f = x^3 + 3*x - 17
sage: f.list()
[-17, 3, 0, 1]
sage: f = PolynomialRing(ZZ,'x')(0)
sage: f.list()
[]

pseudo_divrem(B)¶

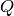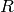Write A = self. This function computes polynomials $Q$ and $R$ and an integer 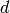$d$ such that

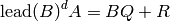
$\mathop{\mathrm{lead}}(B)^d A = B Q + R$

where R has degree less than that of B.

INPUT:

B – a polynomial over $\ZZ$

OUTPUT:

Q, R – polynomials
d – nonnegative integer

EXAMPLES:

sage: R.<x> = ZZ['x']
sage: A = R(range(10)); B = 3*R([-1, 0, 1])
sage: Q, R, d = A.pseudo_divrem(B)
sage: Q, R, d
(9*x^7 + 8*x^6 + 16*x^5 + 14*x^4 + 21*x^3 + 18*x^2 + 24*x + 20, 75*x + 60, 1)
sage: B.leading_coefficient()^d * A == B*Q + R
True

quo_rem(right)¶

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

real_root_intervals()¶

Returns isolating intervals for the real roots of this polynomial.

EXAMPLE: We compute the roots of the characteristic polynomial of some Salem numbers:

sage: R.<x> = PolynomialRing(ZZ)
sage: f = 1 - x^2 - x^3 - x^4 + x^6
sage: f.real_root_intervals()
[((1/2, 3/4), 1), ((1, 3/2), 1)]

resultant(other, proof=True)¶

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

reverse(degree=None)¶

Return a polynomial with the coefficients of this polynomial reversed.

If an optional degree argument is given the coefficient list will be truncated or zero padded as necessary and the reverse polynomial will have the specified degree.

EXAMPLES:

sage: R.<x> = ZZ[]
sage: p = R([1,2,3,4]); p
4*x^3 + 3*x^2 + 2*x + 1
sage: p.reverse()
x^3 + 2*x^2 + 3*x + 4
sage: p.reverse(degree=6)
x^6 + 2*x^5 + 3*x^4 + 4*x^3
sage: p.reverse(degree=2)
x^2 + 2*x + 3

TESTS:

sage: p.reverse(degree=1.5r)
...
ValueError: degree argument must be a non-negative integer, got 1.5

squarefree_decomposition()¶

Return the square-free decomposition of self. This is a partial factorization of self into square-free, relatively prime polynomials.

This is a wrapper for the NTL function SquareFreeDecomp.

EXAMPLES:

sage: R.<x> = PolynomialRing(ZZ)
sage: p = (x-1)^2 * (x-2)^2 * (x-3)^3 * (x-4)
sage: p.squarefree_decomposition()
(x - 4) * (x^2 - 3*x + 2)^2 * (x - 3)^3
sage: p = 37 * (x-1)^2 * (x-2)^2 * (x-3)^3 * (x-4)
sage: p.squarefree_decomposition()
(37) * (x - 4) * (x^2 - 3*x + 2)^2 * (x - 3)^3

xgcd(right)¶

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

sage.rings.polynomial.polynomial_integer_dense_flint.clear_mpz_globals()¶

sage.rings.polynomial.polynomial_integer_dense_flint.gmp_randrange(n1, n2)¶

sage.rings.polynomial.polynomial_integer_dense_flint.init_mpz_globals()¶

Dense univariate polynomials over $\ZZ$ , implemented using FLINT.¶

Previous topic

Next topic

This Page

Navigation

Dense univariate polynomials over , implemented using FLINT.¶

Previous topic

Next topic

This Page

Quick search

Navigation

Dense univariate polynomials over $\ZZ$ , implemented using FLINT.¶