AUTHORS:
TESTS:
We test coercion in a particularly complicated situation:
sage: W.<w>=QQ['w']
sage: WZ.<z>=W['z']
sage: m = matrix(WZ,2,2,[1,z,z,z^2])
sage: a = m.charpoly()
sage: R.<x> = WZ[]
sage: R(a)
x^2 + (-z^2 - 1)*x
Bases: sage.rings.polynomial.polynomial_element.Polynomial, sage.structure.element.IntegralDomainElement
Return True if this polynomial is a unit.
EXERCISE (Atiyah-McDonald, Ch 1): Let ![A[x]](../../../_images/math/4d57b2e7466f9447d4489dc8ef949681ab435b45.png) be a polynomial
ring in one variable. Then
be a polynomial
ring in one variable. Then ![f=\sum a_i x^i \in A[x]](../../../_images/math/226bd1330dd49ad17a9094a0ff3325bd0f11826a.png) is a
unit if and only if
is a
unit if and only if 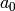 is a unit and
is a unit and 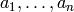 are
nilpotent.
are
nilpotent.
EXAMPLES:
sage: R.<z> = PolynomialRing(ZZ, sparse=True)
sage: (2 + z^3).is_unit()
False
sage: f = -1 + 3*z^3; f
3*z^3 - 1
sage: f.is_unit()
False
sage: R(-3).is_unit()
False
sage: R(-1).is_unit()
True
sage: R(0).is_unit()
False
Bases: sage.rings.polynomial.polynomial_singular_interface.Polynomial_singular_repr, sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_domain, sage.structure.element.EuclideanDomainElement
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Bases: sage.rings.polynomial.polynomial_element.Polynomial
A generic sparse polynomial.
EXAMPLES:
sage: R.<x> = PolynomialRing(PolynomialRing(QQ, 'y'), sparse=True)
sage: f = x^3 - x + 17
sage: type(f)
<class 'sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_sparse'>
sage: loads(f.dumps()) == f
True
A more extensive example:
sage: A.<T> = PolynomialRing(Integers(5),sparse=True) ; f = T^2+1 ; B = A.quo(f)
sage: C.<s> = PolynomialRing(B)
sage: C
Univariate Polynomial Ring in s over Univariate Quotient Polynomial Ring in Tbar over Ring of integers modulo 5 with modulus T^2 + 1
sage: s + T
s + Tbar
sage: (s + T)**2
s^2 + 2*Tbar*s + 4
Return the coefficients of the monomials appearing in self.
EXAMPLES:
sage: R.<w> = PolynomialRing(Integers(8), sparse=True)
sage: f = 5 + w^1997 - w^10000; f
7*w^10000 + w^1997 + 5
sage: f.coefficients()
[5, 1, 7]
Return the degree of this sparse polynomial.
EXAMPLES:
sage: R.<z> = PolynomialRing(ZZ, sparse=True)
sage: f = 13*z^50000 + 15*z^2 + 17*z
sage: f.degree()
50000
Return a new copy of the dict of the underlying elements of self.
EXAMPLES:
sage: R.<w> = PolynomialRing(Integers(8), sparse=True)
sage: f = 5 + w^1997 - w^10000; f
7*w^10000 + w^1997 + 5
sage: d = f.dict(); d
{0: 5, 10000: 7, 1997: 1}
sage: d[0] = 10
sage: f.dict()
{0: 5, 10000: 7, 1997: 1}
Return the exponents of the monomials appearing in self.
EXAMPLES:
sage: R.<w> = PolynomialRing(Integers(8), sparse=True)
sage: f = 5 + w^1997 - w^10000; f
7*w^10000 + w^1997 + 5
sage: f.exponents()
[0, 1997, 10000]
Return a new copy of the list of the underlying elements of self.
EXAMPLES:
sage: R.<z> = PolynomialRing(Integers(100), sparse=True)
sage: f = 13*z^5 + 15*z^2 + 17*z
sage: f.list()
[0, 17, 15, 0, 0, 13]
Returns this polynomial multiplied by the power 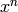 . If
. If  is negative,
terms below
is negative,
terms below 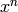 will be discarded. Does not change this polynomial.
will be discarded. Does not change this polynomial.
EXAMPLES:
sage: R.<x> = PolynomialRing(ZZ, sparse=True)
sage: p = x^100000 + 2*x + 4
sage: type(p)
<class 'sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_sparse'>
sage: p.shift(0)
x^100000 + 2*x + 4
sage: p.shift(-1)
x^99999 + 2
sage: p.shift(-100002)
0
sage: p.shift(2)
x^100002 + 2*x^3 + 4*x^2
AUTHOR: - David Harvey (2006-08-06)
EXAMPLES:
sage: R.<w> = PolynomialRing(GF(9,'a'), sparse=True)
sage: f = w^1997 - w^10000
sage: f.valuation()
1997
sage: R(19).valuation()
0
sage: R(0).valuation()
+Infinity
Bases: sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_sparse, sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_field
EXAMPLES:
sage: R.<x> = PolynomialRing(Frac(RR['t']), sparse=True)
sage: f = x^3 - x + 17
sage: type(f)
<class 'sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_sparse_field'>
sage: loads(f.dumps()) == f
True
Bases: sage.rings.polynomial.polynomial_element_generic.Polynomial_padic_generic_dense, sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_dense_field
Bases: sage.rings.polynomial.polynomial_element.Polynomial_generic_dense, sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_domain
This function replaces coefficients of the polynomial that evaluate as equal to 0 with the zero element of the base ring that has the maximum possible precision.
WARNING: this function mutates the underlying polynomial.
Bases: sage.rings.polynomial.polynomial_element_generic.Polynomial_padic_generic_dense
Bases: sage.rings.polynomial.polynomial_element_generic.Polynomial_generic_field
A dense polynomial over the rational numbers.
Return the degree of this polynomial. The zero polynomial has degree -1.
EXAMPLES:
sage: R.<x> = QQ[]
sage: (x^5 + 17*x^3 + x+ 3).degree()
5
sage: R(0).degree()
-1
sage: type(x.degree())
<type 'sage.rings.integer.Integer'>
Returns the denominator of self as an element of  .
.
EXAMPLES:
sage: R.<x> = QQ[]
sage: (x/2).denominator()
2
sage: (x/2 + 1/3).denominator()
6
sage: R.<x> = QQ[]
sage: f = R.random_element(50)
sage: f * f.denominator() in ZZ['x']
True
Same as discriminant().
EXAMPLES:
sage: _.<x> = PolynomialRing(QQ)
sage: f = x^3 + 3*x - 17
sage: f.disc()
-7911
EXAMPLES:
sage: _.<x> = PolynomialRing(QQ)
sage: f = x^3 + 3*x - 17
sage: f.discriminant()
-7911
Return the factorization of self modulo the prime p.
INPUT:
OUTPUT:
factorization of self reduced modulo p.
EXAMPLES:
sage: R.<x> = QQ[]
sage: (x^5 + 17*x^3 + x+ 3).factor_mod(3)
x * (x^2 + 1)^2
sage: (x^5 + 2).factor_mod(5)
(x + 2)^5
Return p-adic factorization of self to given precision.
INPUT:
OUTPUT:
factorization of self viewed as a polynomial over the p-adics
EXAMPLES:
sage: R.<x> = QQ[]
sage: f = x^3 - 2
sage: f.factor_padic(2)
(1 + O(2^10))*x^3 + (O(2^10))*x^2 + (O(2^10))*x + (2 + 2^2 + 2^3 + 2^4 + 2^5 + 2^6 + 2^7 + 2^8 + 2^9 + O(2^10))
sage: f.factor_padic(3)
(1 + O(3^10))*x^3 + (O(3^10))*x^2 + (O(3^10))*x + (1 + 2*3 + 2*3^2 + 2*3^3 + 2*3^4 + 2*3^5 + 2*3^6 + 2*3^7 + 2*3^8 + 2*3^9 + O(3^10))
sage: f.factor_padic(5)
((1 + O(5^10))*x + (2 + 4*5 + 2*5^2 + 2*5^3 + 5^4 + 3*5^5 + 4*5^7 + 2*5^8 + 5^9 + O(5^10))) * ((1 + O(5^10))*x^2 + (3 + 2*5^2 + 2*5^3 + 3*5^4 + 5^5 + 4*5^6 + 2*5^8 + 3*5^9 + O(5^10))*x + (4 + 5 + 2*5^2 + 4*5^3 + 4*5^4 + 3*5^5 + 3*5^6 + 4*5^7 + 4*5^9 + O(5^10)))
Return the Galois group of f as a permutation group.
INPUT:
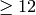 when 'kash' is tried). NOTE:
'magma' also does not return a proven correct result. Please see
the Magma docs for how to get a proven result.
when 'kash' is tried). NOTE:
'magma' also does not return a proven correct result. Please see
the Magma docs for how to get a proven result.ALGORITHM: The Galois group is computed using PARI in C library mode, or possibly kash or magma.
Note
The PARI documentation contains the following warning: The method used is that of resolvent polynomials and is sensitive to the current precision. The precision is updated internally but, in very rare cases, a wrong result may be returned if the initial precision was not sufficient.
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: f = x^4 - 17*x^3 - 2*x + 1
sage: G = f.galois_group(); G # optional - database_gap
Transitive group number 5 of degree 4
sage: G.gens() # optional - database_gap
[(1,2,3,4), (1,2)]
sage: G.order() # optional - database_gap
24
It is potentially useful to instead obtain the corresponding PARI group, which is little more than a 4-tuple. See the PARI manual for the exact details. (Note that the third entry in the tuple is in the new standard ordering.)
sage: f = x^4 - 17*x^3 - 2*x + 1
sage: G = f.galois_group(pari_group=True); G
PARI group [24, -1, 5, "S4"] of degree 4
sage: PermutationGroup(G) # optional - database_gap
Transitive group number 5 of degree 4
You can use KASH to compute Galois groups as well. The advantage is that KASH can compute Galois groups of fields up to degree 23, whereas PARI only goes to degree 11. (In my not-so-thorough experiments PARI is faster than KASH.)
sage: f = x^4 - 17*x^3 - 2*x + 1
sage: f.galois_group(algorithm='kash') # optional - kash
Transitive group number 5 of degree 4
sage: f = x^4 - 17*x^3 - 2*x + 1
sage: f.galois_group(algorithm='magma') # optional - magma, database_gap
Transitive group number 5 of degree 4
 into distinct factors,
computes the Hensel lifts of these factors modulo
into distinct factors,
computes the Hensel lifts of these factors modulo 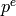 . We
assume that
. We
assume that  has integer coefficients.
has integer coefficients.EXAMPLES:
sage: R.<x> = QQ[]
sage: (x^2 + 2).is_irreducible()
True
sage: (x^2 - 1).is_irreducible()
False
See trac #5140:
sage: (2*x).is_irreducible()
True
Return a new copy of the list of the underlying elements of self.
EXAMPLES:
sage: _.<x> = PolynomialRing(QQ)
sage: f = x^3 + 3*x - 17/13; f
x^3 + 3*x - 17/13
sage: v = f.list(); v
[-17/13, 3, 0, 1]
sage: v[0] = 0
sage: f
x^3 + 3*x - 17/13
sage: f.list()
[-17/13, 3, 0, 1]
Returns the numerator of self as a polynomial in ![\ZZ[x]](../../../_images/math/997bd738c8f73a5487d82a0af9f18a75a09c06ec.png) .
.
EXAMPLES:
sage: R.<x> = QQ[]
sage: (x/2).numerator()
x
sage: (x + 1/2).numerator()
2*x + 1
sage: (x^2/12 - 1/15).numerator()
5*x^2 - 4
sage: f = R.random_element(60)
sage: f.numerator() in ZZ['x']
True
sage: f.numerator() / f.denominator() == f
True
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Returns isolating intervals for the real roots of this polynomial.
EXAMPLE:
sage: R.<x> = PolynomialRing(QQ)
sage: f = (x - 1/2) * (x - 3/4) * (x - 3/2)
sage: f.real_root_intervals()
[((243/512, 1215/2048), 1), ((729/1024, 1701/2048), 1), ((243/256, 1011/512), 1)]
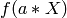 .
.