Boolean Polynomials

Elements of the quotient ring

are called boolean polynomials. Boolean polynomials arise naturally in cryptography, coding theory, formal logic, chip design and other areas. This implementation is a thin wrapper around the PolyBoRi library by Michael Brickenstein and Alexander Dreyer.

“Boolean polynomials can be modelled in a rather simple way, with both coefficients and degree per variable lying in {0, 1}. The ring of Boolean polynomials is, however, not a polynomial ring, but rather the quotient ring of the polynomial ring over the field with two elements modulo the field equations 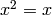for each variable . Therefore, the usual polynomial data structures seem not to be appropriate for fast Groebner basis computations. We introduce a specialised data structure for Boolean polynomials based on zero-suppressed binary decision diagrams (ZDDs), which is capable of handling these polynomials more efficiently with respect to memory consumption and also computational speed. Furthermore, we concentrate on high-level algorithmic aspects, taking into account the new data structures as well as structural properties of Boolean polynomials.” - [BD07]

For details on the internal representation of polynomials see

http://polybori.sourceforge.net/zdd.html

AUTHORS:

• Michael Brickenstein: PolyBoRi author
• Alexander Dreyer: PolyBoRi author
• Burcin Erocal <burcin@erocal.org>: main Sage wrapper author
• Martin Albrecht <malb@informatik.uni-bremen.de>: some contributions to the Sage wrapper

EXAMPLES:

Consider the ideal

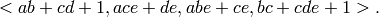
First, we compute the lexicographical Groebner basis in the polynomial ring

sage: P.<a,b,c,d,e> = PolynomialRing(GF(2), 5, order='lex')
sage: I1 = ideal([a*b + c*d + 1, a*c*e + d*e, a*b*e + c*e, b*c + c*d*e + 1])
sage: for f in I1.groebner_basis():
...     f
a + c^2*d + c + d^2*e
b*c + d^3*e^2 + d^3*e + d^2*e^2 + d*e + e + 1
b*e + d*e^2 + d*e + e
c*e + d^3*e^2 + d^3*e + d^2*e^2 + d*e
d^4*e^2 + d^4*e + d^3*e + d^2*e^2 + d^2*e + d*e + e

If one wants to solve this system over the algebraic closure of 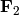then this Groebner basis was the one to consider. If one wants solutions over 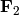only then one adds the field polynomials to the ideal to force the solutions in .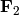

sage: J = I1 + sage.rings.ideal.FieldIdeal(P)
sage: for f in J.groebner_basis():
...     f
a + d + 1
b + 1
c + 1
d^2 + d
e

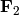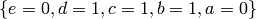So the solutions over are and .

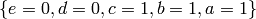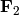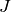We can express the restriction to by considering the quotient ring. If is an ideal in then the ideals in the quotient ring are in one-to-one correspondence with the ideals of containing (that is, the ideals satisfying ).

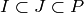sage: Q = P.quotient( sage.rings.ideal.FieldIdeal(P) )
sage: I2 = ideal([Q(f) for f in I1.gens()])
sage: for f in I2.groebner_basis():
...     f
abar + dbar + 1
bbar + 1
cbar + 1
ebar

This quotient ring is exactly what PolyBoRi handles well:

sage: B.<a,b,c,d,e> = BooleanPolynomialRing(5, order='lex')
sage: I2 = ideal([B(f) for f in I1.gens()])
sage: for f in I2.groebner_basis(): 
...     f
a + d + 1
b + 1
c + 1
e

Note that d^2 + d is not representable in B == Q. Also note, that PolyBoRi cannot play out its strength in such small examples, i.e. working in the polynomial ring might be faster for small examples like this.

Implementation specific notes

PolyBoRi comes with a Python wrapper. However this wrapper does not match Sage’s style and is written using Boost. Thus Sage’s wrapper is a reimplementation of Python bindings to PolyBoRi’s C++ library. This interface is written in Cython like all of Sage’s C/C++ library interfaces. An interface in PolyBoRi style is also provided which is effectively a reimplementation of the official Boost wrapper in Cython. This means that some functionality of the official wrapper might be missing from this wrapper and this wrapper might have bugs not present in the official Python interface.

Access to the original PolyBoRi interface

The re-implementation PolyBoRi’s native wrapper is available to the user too:

sage: from polybori import *
sage: declare_ring([Block('x',2),Block('y',3)],globals())
Boolean PolynomialRing in x(0), x(1), y(0), y(1), y(2)
sage: r
Boolean PolynomialRing in x(0), x(1), y(0), y(1), y(2)

sage: [Variable(i) for i in xrange(r.ngens())]
[x(0), x(1), y(0), y(1), y(2)]

For details on this interface see:

http://polybori.sourceforge.net/doc/tutorial/tutorial.html.

Also, the interface provides functions for compatibility with Sage accepting convenient Sage data types which are slower than their native PolyBoRi counterparts. For instance, sets of points can be represented as tuples of tuples (Sage) or as BooleSet (PolyBoRi) and naturally the second option is faster.

REFERENCES:

[BD07]

Michael Brickenstein, Alexander Dreyer; PolyBoRi: A Groebner basis framework for Boolean polynomials; pre-print available at http://www.itwm.fraunhofer.de/zentral/download/berichte/bericht122.pdf

class sage.rings.polynomial.pbori.BooleSet

Bases: object

Return a new set of boolean monomials. This data type is also implemented on the top of ZDDs and allows to see polynomials from a different angle. Also, it makes high-level set operations possible, which are in most cases faster than operations handling individual terms, because the complexity of the algorithms depends only on the structure of the diagrams.

Objects of type BooleanPolynomial can easily be converted to the type BooleSet by using the member function BooleanPolynomial.set().

INPUT:

• param - either a CCuddNavigator, a BooleSet or None.
• ring - a boolean polynomial ring.

EXAMPLE:

sage: from polybori import BooleSet
sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: BS = BooleSet(a.set())
sage: BS
{{a}}

sage: BS = BooleSet((a*b + c + 1).set())
sage: BS
{{a,b}, {c}, {}}

sage: from polybori import *
sage: BooleSet([Monomial()])
{{}}

Note

BooleSet prints as {} but are not Python dictionaries.

cartesian_product(rhs)

Return the Cartesian product of this set and the set rhs.

The Cartesian product of two sets X and Y is the set of all possible ordered pairs whose first component is a member of X and whose second component is a member of Y.

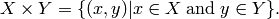
EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3
sage: s = f.set(); s
{{x1,x2}, {x2,x3}}
sage: g = x4 + 1
sage: t = g.set(); t
{{x4}, {}}
sage: s.cartesian_product(t)
{{x1,x2,x4}, {x1,x2}, {x2,x3,x4}, {x2,x3}}

change(ind)

Swaps the presence of x_i in each entry of the set.

EXAMPLE:

sage: P.<a,b,c> = BooleanPolynomialRing()
sage: f = a+b
sage: s = f.set(); s
{{a}, {b}}
sage: s.change(0)
{{a,b}, {}}
sage: s.change(1)
{{a,b}, {}}
sage: s.change(2)
{{a,c}, {b,c}}

diff(rhs)

Return the set theoretic difference of this set and the set rhs.

The difference of two sets and 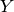is defined as:

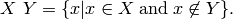
EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3
sage: s = f.set(); s
{{x1,x2}, {x2,x3}}
sage: g = x2*x3 + 1
sage: t = g.set(); t
{{x2,x3}, {}}
sage: s.diff(t)
{{x1,x2}}

divide(rhs)

Divide each element of this set by the monomial rhs and return a new set containing the result.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing(order='lex')
sage: f = b*e + b*c*d + b
sage: s = f.set(); s
{{b,c,d}, {b,e}, {b}}
sage: s.divide(b.lm())
{{c,d}, {e}, {}}

sage: f = b*e + b*c*d + b + c
sage: s = f.set()
sage: s.divide(b.lm())
{{c,d}, {e}, {}}

empty()

Return True if this set is empty.

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: BS = (a*b + c).set()
sage: BS.empty()
False

sage: BS = B(0).set()
sage: BS.empty()
True

include_divisors()

Extend this set to include all divisors of the elements already in this set and return the result as a new set.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: f = a*d*e + a*f + b*d*e + c*d*e + 1
sage: s = f.set(); s
{{a,d,e}, {a,f}, {b,d,e}, {c,d,e}, {}}

sage: s.include_divisors()
{{a,d,e}, {a,d}, {a,e}, {a,f}, {a}, {b,d,e}, {b,d}, {b,e}, 
 {b}, {c,d,e}, {c,d}, {c,e}, {c}, {d,e}, {d}, {e}, {f}, {}}

intersect(other)

Return the set theoretic intersection of this set and the set rhs.

The union of two sets and 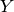is defined as:

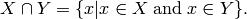
EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3
sage: s = f.set(); s
{{x1,x2}, {x2,x3}}
sage: g = x2*x3 + 1
sage: t = g.set(); t
{{x2,x3}, {}}
sage: s.intersect(t)
{{x2,x3}}

minimal_elements()

Return a new set containing a divisor of all elements of this set.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: f = a*d*e + a*f + a*b*d*e + a*c*d*e + a
sage: s = f.set(); s
{{a,b,d,e}, {a,c,d,e}, {a,d,e}, {a,f}, {a}}
sage: s.minimal_elements()
{{a}}

multiples_of(m)

Return those members which are multiples of m.

INPUT:

• m - a boolean monomial

EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3
sage: s = f.set()
sage: s.multiples_of(x1.lm())
{{x1,x2}}

n_nodes()

Return the number of nodes in the ZDD.

EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3
sage: s = f.set(); s
{{x1,x2}, {x2,x3}}
sage: s.n_nodes()
4

navigation()

Navigators provide an interface to diagram nodes, accessing their index as well as the corresponding then- and else-branches.

You should be very careful and always keep a reference to the original object, when dealing with navigators, as navigators contain only a raw pointer as data. For the same reason, it is necessary to supply the ring as argument, when constructing a set out of a navigator.

EXAMPLE:

sage: from polybori import BooleSet
sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3*x4+x2*x4+x3+x4+1
sage: s = f.set(); s
{{x1,x2}, {x2,x3,x4}, {x2,x4}, {x3}, {x4}, {}}

sage: nav = s.navigation()
sage: BooleSet(nav,s.ring())
{{x1,x2}, {x2,x3,x4}, {x2,x4}, {x3}, {x4}, {}}

sage: nav.value()
1

sage: nav_else = nav.else_branch()

sage: BooleSet(nav_else,s.ring())
{{x2,x3,x4}, {x2,x4}, {x3}, {x4}, {}}

sage: nav_else.value()
2

ring()

Return the parent ring.

EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3*x4+x2*x4+x3+x4+1
sage: f.set().ring() is B
True

set()

Return self.

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: BS = (a*b + c).set()
sage: BS.set() is BS
True

size_double()

Return the size of this set as a floating point number.

EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3
sage: s = f.set()
sage: s.size_double()
2.0

stable_hash()

A hash value which is stable across processes.

EXAMPLE:

sage: B.<x,y> = BooleanPolynomialRing()
sage: s = x.set()
sage: s.stable_hash()
-845955105                 # 32-bit
173100285919               # 64-bit

Note

This function is part of the upstream PolyBoRi interface. In Sage all hashes are stable.

subset0(i)

Return a set of those elements in this set which do not contain the variable indexed by i.

INPUT:

• i - an index

EXAMPLE:

sage: BooleanPolynomialRing(5,'x')
Boolean PolynomialRing in x0, x1, x2, x3, x4
sage: B = BooleanPolynomialRing(5,'x')
sage: B.inject_variables()
Defining x0, x1, x2, x3, x4
sage: f = x1*x2+x2*x3
sage: s = f.set(); s
{{x1,x2}, {x2,x3}}
sage: s.subset0(1)
{{x2,x3}}

subset1(i)

Return a set of those elements in this set which do contain the variable indexed by i and evaluate the variable indexed by i to 1.

INPUT:

• i - an index

EXAMPLE:

sage: BooleanPolynomialRing(5,'x')
Boolean PolynomialRing in x0, x1, x2, x3, x4
sage: B = BooleanPolynomialRing(5,'x')
sage: B.inject_variables()
Defining x0, x1, x2, x3, x4
sage: f = x1*x2+x2*x3
sage: s = f.set(); s
{{x1,x2}, {x2,x3}}
sage: s.subset1(1)
{{x2}}

union(rhs)

Return the set theoretic union of this set and the set rhs.

The union of two sets and 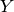is defined as:

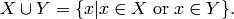
EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3
sage: s = f.set(); s
{{x1,x2}, {x2,x3}}
sage: g = x2*x3 + 1
sage: t = g.set(); t
{{x2,x3}, {}}
sage: s.union(t)
{{x1,x2}, {x2,x3}, {}}

vars()

Return the variables in this set as a monomial.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing(order='lex')
sage: f = a + b*e + d*f + e + 1
sage: s = f.set()
sage: s
{{a}, {b,e}, {d,f}, {e}, {}}
sage: s.vars()
a*b*d*e*f

class sage.rings.polynomial.pbori.BooleSetIterator

Bases: object

Helper class to iterate over boolean sets.

next()

x.next() -> the next value, or raise StopIteration

class sage.rings.polynomial.pbori.BooleanMonomial

Bases: sage.structure.element.MonoidElement

Construct a boolean monomial.

INPUT:

• parent - parent monoid this element lives in

EXAMPLE:

sage: from polybori import BooleanMonomialMonoid, BooleanMonomial
sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: M = BooleanMonomialMonoid(P)
sage: BooleanMonomial(M)
1

Note

Use the BooleanMonomialMonoid__call__() method and not this constructor to construct these objects.

deg()

Return degree of this monomial.

EXAMPLES:

sage: from polybori import BooleanMonomialMonoid
sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: M = BooleanMonomialMonoid(P)
sage: M(x*y).deg()
2

sage: M(x*x*y*z).deg()
3

Note

This function is part of the upstream PolyBoRi interface.

degree()

Return degree of this monomial.

EXAMPLES:

sage: from polybori import BooleanMonomialMonoid
sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: M = BooleanMonomialMonoid(P)
sage: M(x*y).degree()
2

divisors()

Return a set of boolean monomials with all divisors of this monomial.

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3)
sage: f = x*y
sage: m = f.lm()
sage: m.divisors()
{{x,y}, {x}, {y}, {}}

gcd(rhs)

A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.

In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.

index()

Return the variable index of the first variable in this monomial.

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3)
sage: f = x*y
sage: m = f.lm()
sage: m.index()
0

Note

This function is part of the upstream PolyBoRi interface.

iterindex()

Return an iterator over the indicies of the variables in self.

EXAMPLES:

sage: from polybori import BooleanMonomialMonoid
sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: M = BooleanMonomialMonoid(P)
sage: list(M(x*z).iterindex())
[0, 2]

multiples(rhs)

Return a set of boolean monomials with all multiples of this monomial up to the bound rhs.

INPUT:

• rhs - a boolean monomial

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3)
sage: f = x
sage: m = f.lm()
sage: g = x*y*z
sage: n = g.lm()
sage: m.multiples(n)
{{x,y,z}, {x,y}, {x,z}, {x}}
sage: n.multiples(m)
{{x,y,z}}

Note

The returned set always contains self even if the bound rhs is smaller than self.

navigation()

Navigators provide an interface to diagram nodes, accessing their index as well as the corresponding then- and else-branches.

You should be very careful and always keep a reference to the original object, when dealing with navigators, as navigators contain only a raw pointer as data. For the same reason, it is necessary to supply the ring as argument, when constructing a set out of a navigator.

EXAMPLE:

sage: from polybori import BooleSet
sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3*x4+x2*x4+x3+x4+1
sage: m = f.lm(); m
x1*x2

sage: nav = m.navigation()
sage: BooleSet(nav, B)
{{x1,x2}}

sage: nav.value()
1

reducible_by(rhs)

Return True if self is reducible by rhs.

INPUT:

• rhs - a boolean monomial

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3)
sage: f = x*y
sage: m = f.lm()
sage: m.reducible_by((x*y).lm())
True
sage: m.reducible_by((x*z).lm())
False

set()

Return a boolean set of variables in this monomials.

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3)
sage: f = x*y
sage: m = f.lm()
sage: m.set()
{{x,y}}

stable_hash()

A hash value which is stable across processes.

EXAMPLE:

sage: B.<x,y> = BooleanPolynomialRing()
sage: m = x.lm()
sage: m.stable_hash()
-845955105                 # 32-bit
173100285919               # 64-bit

Note

This function is part of the upstream PolyBoRi interface. In Sage all hashes are stable.

variables()

Return a tuple of the variables in this monomial.

EXAMPLE:

sage: from polybori import BooleanMonomialMonoid
sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: M = BooleanMonomialMonoid(P)
sage: M(x*z).variables() # indirect doctest
(x, z)

class sage.rings.polynomial.pbori.BooleanMonomialIterator

Bases: object

An iterator over the variable indices of a monomial.

next()

x.next() -> the next value, or raise StopIteration

class sage.rings.polynomial.pbori.BooleanMonomialMonoid

Bases: sage.monoids.monoid.Monoid_class

Construct a boolean monomial monoid given a boolean polynomial ring.

This object provides a parent for boolean monomials.

INPUT:

• polring - the polynomial ring our monomials lie in

EXAMPLES:

sage: from polybori import BooleanMonomialMonoid
sage: P.<x,y> = BooleanPolynomialRing(2)
sage: M = BooleanMonomialMonoid(P)
sage: M
MonomialMonoid of Boolean PolynomialRing in x, y

sage: M.gens()
(x, y)
sage: type(M.gen(0))
<type 'sage.rings.polynomial.pbori.BooleanMonomial'>

gen(i=0)

Return the i-th generator of self.

INPUT:

• i - an integer

EXAMPLES:

sage: from polybori import BooleanMonomialMonoid
sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: M = BooleanMonomialMonoid(P)
sage: M.gen(0)
x
sage: M.gen(2)
z

sage: P = BooleanPolynomialRing(1000, 'x')
sage: M = BooleanMonomialMonoid(P)
sage: M.gen(50)
x50

gens()

Return the tuple of generators of this monoid.

EXAMPLES:

sage: from polybori import BooleanMonomialMonoid
sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: M = BooleanMonomialMonoid(P)
sage: M.gens()
(x, y, z)

ngens()

Returns the number of variables in this monoid.

EXAMPLES:

sage: from polybori import BooleanMonomialMonoid
sage: P = BooleanPolynomialRing(100, 'x')
sage: M = BooleanMonomialMonoid(P)
sage: M.ngens()
100

class sage.rings.polynomial.pbori.BooleanMonomialVariableIterator

Bases: object

next()

x.next() -> the next value, or raise StopIteration

class sage.rings.polynomial.pbori.BooleanMulAction

Bases: sage.categories.action.Action

class sage.rings.polynomial.pbori.BooleanPolynomial

Bases: sage.rings.polynomial.multi_polynomial.MPolynomial

Construct a boolean polynomial object in the given boolean polynomial ring.

INPUT:

• parent - a boolean polynomial ring

TEST:

sage: from polybori import BooleanPolynomial
sage: B.<a,b,z> = BooleanPolynomialRing(3)
sage: BooleanPolynomial(B)
0

Note

Do not use this method to construct boolean polynomials, but use the appropriate __call__ method in the parent.

constant()

Return True if this element is constant.

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3)
sage: x.constant()
False

sage: B(1).constant()
True

Note

This function is part of the upstream PolyBoRi interface.

constant_coefficient()

Returns the constant coefficient of this boolean polynomial.

EXAMPLE:

sage: B.<a,b> = BooleanPolynomialRing()
sage: a.constant_coefficient()
0
sage: (a+1).constant_coefficient()
1

deg()

Return the degree of self. This is usually equivalent to the total degree except for weighted term orderings which are not implemented yet.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: (x+y).degree()
1

sage: P(1).degree()
0

sage: (x*y + x + y + 1).degree()
2

Note

This function is part of the upstream PolyBoRi interface.

degree()

Return the total degree of self.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: (x+y).degree()
1

sage: P(1).degree()
0

sage: (x*y + x + y + 1).degree()
2

elength()

Return elimination length as used in the SlimGB algorithm.

EXAMPLE:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: x.elength()
1
sage: f = x*y + 1
sage: f.elength()
2

REFERENCES:

• Michael Brickenstein; SlimGB: Groebner Bases with Slim Polynomials http://www.mathematik.uni-kl.de/~zca/Reports_on_ca/35/paper_35_full.ps.gz

Note

This function is part of the upstream PolyBoRi interface.

first_term()

Return the first term with respect to the lexicographical term ordering.

EXAMPLE:

sage: B.<a,b,z> = BooleanPolynomialRing(3,order='lex')
sage: f = b*z + a + 1
sage: f.first_term()
a

Note

This function is part of the upstream PolyBoRi interface.

graded_part(deg)

Return graded part of this boolean polynomial of degree deg.

INPUT:

• deg - a degree

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: f = a*b*c + c*d + a*b + 1
sage: f.graded_part(2)
a*b + c*d

sage: f.graded_part(0)
1

TESTS:

sage: f.graded_part(-1)
0

has_constant_part()

Return True if this boolean polynomial has a constant part, i.e. if 1 is a term.

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: f = a*b*c + c*d + a*b + 1
sage: f.has_constant_part()
True

sage: f = a*b*c + c*d + a*b
sage: f.has_constant_part()
False

is_constant()

Check if self is constant.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: P(1).is_constant()
True

sage: P(0).is_constant()
True

sage: x.is_constant()
False

sage: (x*y).is_constant()
False

is_equal(right)

EXAMPLE:

sage: B.<a,b,z> = BooleanPolynomialRing(3)
sage: f = a*z + b + 1
sage: g = b + z
sage: f.is_equal(g)
False

sage: f.is_equal( (f + 1) - 1 )
True

Note

This function is part of the upstream PolyBoRi interface.

is_homogeneous()

Return True if this element is a homogeneous polynomial.

EXAMPLES:

sage: P.<x, y> = BooleanPolynomialRing()
sage: (x+y).is_homogeneous()
True 
sage: P(0).is_homogeneous() 
True 
sage: (x+1).is_homogeneous()
False

is_one()

Check if self is 1.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: P(1).is_one()
True

sage: P.one_element().is_one()
True

sage: x.is_one()
False

sage: P(0).is_one()
False

is_unit()

Check if self is invertible in the parent ring.

Note that this condition is equivalent to being 1 for boolean polynomials.

EXAMPLE:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: P.one_element().is_unit()
True

sage: x.is_unit()
False

is_zero()

Check if self is zero.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: P(0).is_zero()
True

sage: x.is_zero()
False

sage: P(1).is_zero()
False

lead()

Return the leading monomial of boolean polynomial, with respect to to the order of parent ring.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: (x+y+y*z).lead()
x

sage: P.<x,y,z> = BooleanPolynomialRing(3, order='deglex')
sage: (x+y+y*z).lead()
y*z

Note

This function is part of the upstream PolyBoRi interface.

lead_deg()

Returns the total degree of the leading monomial of self.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: p = x + y*z
sage: p.lead_deg()
1

sage: P.<x,y,z> = BooleanPolynomialRing(3,order='deglex')
sage: p = x + y*z
sage: p.lead_deg()
2

sage: P(0).lead_deg()
0

Note

This function is part of the upstream PolyBoRi interface.

lead_divisors()

Return a BooleSet of all divisors of the leading monomial.

EXAMPLE:

sage: B.<a,b,z> = BooleanPolynomialRing(3)
sage: f = a*b + z + 1
sage: f.lead_divisors()
{{a,b}, {a}, {b}, {}}

Note

This function is part of the upstream PolyBoRi interface.

lex_lead()

Return the leading monomial of boolean polynomial, with respect to the lexicographical term ordering.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: (x+y+y*z).lex_lead()
x

sage: P.<x,y,z> = BooleanPolynomialRing(3, order='deglex')
sage: (x+y+y*z).lex_lead()
x

Note

This function is part of the upstream PolyBoRi interface.

lex_lead_deg()

Return degree of leading monomial with respect to the lexicographical ordering.

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3,order='lex')
sage: f = x + y*z
sage: f
x + y*z
sage: f.lex_lead_deg()
1

sage: B.<x,y,z> = BooleanPolynomialRing(3,order='deglex')
sage: f = x + y*z
sage: f
y*z + x
sage: f.lex_lead_deg()
1

Note

This function is part of the upstream PolyBoRi interface.

lm()

Return the leading monomial of this boolean polynomial, with respect to the order of parent ring.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: (x+y+y*z).lm()
x

sage: P.<x,y,z> = BooleanPolynomialRing(3, order='deglex')
sage: (x+y+y*z).lm()
y*z

sage: P(0).lm()
0

lt()

Return the leading term of this boolean polynomial, with respect to the order of the parent ring.

Note that for boolean polynomials this is equivalent to returning leading monomials.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: (x+y+y*z).lt()
x

sage: P.<x,y,z> = BooleanPolynomialRing(3, order='deglex')
sage: (x+y+y*z).lt()
y*z

map_every_x_to_x_plus_one()

Map every variable x_i in this polynomial to x_i + 1.

EXAMPLE:

sage: B.<a,b,z> = BooleanPolynomialRing(3)
sage: f = a*b + z + 1; f
a*b + z + 1
sage: f.map_every_x_to_x_plus_one()
a*b + a + b + z + 1
sage: f(a+1,b+1,z+1)
a*b + a + b + z + 1

monomial_coefficient(mon)

Return the coefficient of the monomial mon in self, where mon must have the same parent as self.

INPUT:

• mon - a monomial

EXAMPLE:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: x.monomial_coefficient(x)
1
sage: x.monomial_coefficient(y)
0
sage: R.<x,y,z,a,b,c>=BooleanPolynomialRing(6)
sage: f=(1-x)*(1+y); f
x*y + x + y + 1

sage: f.monomial_coefficient(1)
1

sage: f.monomial_coefficient(0)
0

monomials()

Return a list of monomials appearing in self ordered largest to smallest.

EXAMPLE:

sage: P.<a,b,c> = BooleanPolynomialRing(3,order='lex') 
sage: f = a + c*b 
sage: f.monomials() 
[a, b*c] 

sage: P.<a,b,c> = BooleanPolynomialRing(3,order='degrevlex') 
sage: f = a + c*b 
sage: f.monomials() 
[c*b, a]

n_nodes()

Return the number of nodes in the ZDD implementing this polynomial.

EXAMPLE:

sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2 + x2*x3 + 1
sage: f.n_nodes()
4

Note

This function is part of the upstream PolyBoRi interface.

n_vars()

Return the number of variables used to form this boolean polynomial.

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: f = a*b*c + 1
sage: f.n_vars()
3

Note

This function is part of the upstream PolyBoRi interface.

navigation()

Navigators provide an interface to diagram nodes, accessing their index as well as the corresponding then- and else-branches.

You should be very careful and always keep a reference to the original object, when dealing with navigators, as navigators contain only a raw pointer as data. For the same reason, it is necessary to supply the ring as argument, when constructing a set out of a navigator.

EXAMPLE:

sage: from polybori import BooleSet
sage: B = BooleanPolynomialRing(5,'x')
sage: x0,x1,x2,x3,x4 = B.gens()
sage: f = x1*x2+x2*x3*x4+x2*x4+x3+x4+1

sage: nav = f.navigation()
sage: BooleSet(nav, B)
{{x1,x2}, {x2,x3,x4}, {x2,x4}, {x3}, {x4}, {}}

sage: nav.value()
1

sage: nav_else = nav.else_branch()

sage: BooleSet(nav_else, B)
{{x2,x3,x4}, {x2,x4}, {x3}, {x4}, {}}

sage: nav_else.value()
2

Note

This function is part of the upstream PolyBoRi interface.

nvariables()

Return the number of variables used to form this boolean polynomial.

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: f = a*b*c + 1
sage: f.nvariables()
3

reduce(I)

Return the normal form of self w.r.t. I, i.e. return the remainder of self with respect to the polynomials in I. If the polynomial set/list I is not a Groebner basis the result is not canonical.

INPUT:

• I - a list/set of polynomials in self.parent(). If I is an ideal, the generators are used.

EXAMPLE:

sage: B.<x0,x1,x2,x3> = BooleanPolynomialRing(4)
sage: I = B.ideal((x0 + x1 + x2 + x3, \
                   x0*x1 + x1*x2 + x0*x3 + x2*x3, \
                   x0*x1*x2 + x0*x1*x3 + x0*x2*x3 + x1*x2*x3, \
                   x0*x1*x2*x3 + 1))
sage: gb = I.groebner_basis()
sage: f,g,h,i = I.gens()
sage: f.reduce(gb)
0
sage: p = f*g + x0*h + x2*i
sage: p.reduce(gb)
0
sage: p.reduce(I)
x1*x2*x3 + x2

Note

If this function is called repeatedly with the same I then it is advised to use PolyBoRi’s GroebnerStrategy object directly, since that will be faster. See the source code of this function for details.

TESTS:

sage: R=BooleanPolynomialRing(20,'x','lex')
sage: a=R.random_element()
sage: a.reduce([None,None])
...
TypeError: argument must be a BooleanPolynomial.

reducible_by(rhs)

Return True if this boolean polynomial is reducible by the polynomial rhs.

INPUT:

• rhs - a boolean polynomial

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4,order='degrevlex')
sage: f = (a*b + 1)*(c + 1)
sage: f.reducible_by(d)
False
sage: f.reducible_by(c)
True
sage: f.reducible_by(c + 1)
True

Note

This function is part of the upstream PolyBoRi interface.

ring()

Return the parent of this boolean polynomial.

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: a.ring() is B
True

set()

Return a BooleSet with all monomials appearing in this polynomial.

EXAMPLE:

sage: B.<a,b,z> = BooleanPolynomialRing(3)
sage: (a*b+z+1).set()
{{a,b}, {z}, {}}

spoly(rhs)

Return the S-Polynomial of this boolean polynomial and the other boolean polynomial rhs.

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: f = a*b*c + c*d + a*b + 1
sage: g = c*d + b
sage: f.spoly(g)
a*b + a*c*d + c*d + 1

Note

This function is part of the upstream PolyBoRi interface.

stable_hash()

A hash value which is stable across processes.

EXAMPLE:

sage: B.<x,y> = BooleanPolynomialRing()
sage: x.stable_hash()
-845955105                 # 32-bit
173100285919               # 64-bit

Note

This function is part of the upstream PolyBoRi interface. In Sage all hashes are stable.

subs(in_dict, **kwds=None)

Fixes some given variables in a given boolean polynomial and returns the changed boolean polynomials. The polynomial itself is not affected. The variable,value pairs for fixing are to be provided as dictionary of the form {variable:value} or named parameters (see examples below).

INPUT:

• in_dict - (optional) dict with variable:value pairs
• **kwds - names parameters

EXAMPLE:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: f = x*y + z + y*z + 1
sage: f.subs(x=1)
y*z + y + z + 1
sage: f.subs(x=0)
y*z + z + 1

sage: f.subs(x=y)
y*z + y + z + 1

sage: f.subs({x:1},y=1)
0
sage: f.subs(y=1)
x + 1
sage: f.subs(y=1,z=1)
x + 1
sage: f.subs(z=1)
x*y + y
sage: f.subs({'x':1},y=1)
0

This method can work fully symbolic:

sage: f.subs(x=var('a'),y=var('b'),z=var('c'))
a*b + b*c + c + 1
sage: f.subs({'x':var('a'),'y':var('b'),'z':var('c')})
a*b + b*c + c + 1

terms()

Return a list of monomials appearing in self ordered largest to smallest.

EXAMPLE:

sage: P.<a,b,c> = BooleanPolynomialRing(3,order='lex') 
sage: f = a + c*b 
sage: f.terms() 
[a, b*c] 

sage: P.<a,b,c> = BooleanPolynomialRing(3,order='degrevlex') 
sage: f = a + c*b 
sage: f.terms() 
[c*b, a]

total_degree()

Return the total degree of self.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: (x+y).total_degree()
1

sage: P(1).total_degree()
0

sage: (x*y + x + y + 1).total_degree()
2

variables()

Return a tuple of all variables appearing in self.

EXAMPLE:

sage: P.<x,y,z> = BooleanPolynomialRing(3)  
sage: (x + y).variables()  
(x, y)

sage: (x*y + z).variables()  
(x, y, z)  

sage: P.zero_element().variables()  
()

sage: P.one_element().variables()  
(1,)

vars_as_monomial()

Return a boolean monomial with all the variables appearing in self.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: (x + y).vars_as_monomial()
x*y

sage: (x*y + z).vars_as_monomial()
x*y*z

sage: P.zero_element().vars_as_monomial()
1

sage: P.one_element().vars_as_monomial()
1

TESTS:

sage: R = BooleanPolynomialRing(1, 'y')
sage: y.vars_as_monomial()
y
sage: R
Boolean PolynomialRing in y

Note

This function is part of the upstream PolyBoRi interface.

zeros_in(s)

Return a set containing all elements of s where this boolean polynomial evaluates to zero.

If s is given as a BooleSet, then the return type is also a BooleSet. If s is a set/list/tuple of tuple this function returns a tuple of tuples.

INPUT:

• s - candidate points for evaluation to zero

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: f = a*b + c + d + 1

Now we create a set of points:

sage: s = a*b + a*b*c + c*d + 1
sage: s = s.set(); s
{{a,b,c}, {a,b}, {c,d}, {}}

This encodes the points (1,1,1,0), (1,1,0,0), (0,0,1,1) and (0,0,0,0). But of these only (1,1,0,0) evaluates to zero.

sage: f.zeros_in(s)
{{a,b}}

sage: f.zeros_in([(1,1,1,0), (1,1,0,0), (0,0,1,1), (0,0,0,0)])
((1, 1, 0, 0),)

class sage.rings.polynomial.pbori.BooleanPolynomialEntry

Bases: object

p

class sage.rings.polynomial.pbori.BooleanPolynomialIdeal

Bases: sage.rings.polynomial.multi_polynomial_ideal.MPolynomialIdeal

groebner_basis(**kwds)

Return a Groebner basis of this ideal.

INPUT:

• red_tail - tail reductions in intermediate polynomials, this options affects mainly heuristics. The reducedness of the output polynomials can only be guaranteed by the option redsb (default: True)

• minsb - return a minimal Groebner basis (default: True)

• redsb - return a minimal Groebner basis and all tails are reduced (default: True)

• deg_bound - only compute Groebner basis up to a given degree bound (default: False)

• faugere - turn off or on the linear algebra (default: False)

• linear_algebra_in_last_block - this affects the last block of block orderings and degree orderings. If it is set to True linear algebra takes affect in this block. (default: True)

• “gauss_on_linear” - perform Gaussian elimination on linear

  polynomials (default: True)

• selection_size - maximum number of polynomials for parallel reductions (default: 1000)

• heuristic - Turn off heuristic by setting heuristic=False (default: True)

• lazy - (default: True)

• invert - setting invert=True input and output get a transformation x+1 for each variable x, which shouldn’t effect the calculated GB, but the algorithm.

• other_ordering_first - possible values are False or an ordering code. In practice, many Boolean examples have very few solutions and a very easy Groebner basis. So, a complex walk algorithm (which cannot be implemented using the data structures) seems unnecessary, as such Groebner bases can be converted quite fast by the normal Buchberger algorithm from one ordering into another ordering. (default: False)

• prot - show protocol (default: False)

• full_prot - show full protocol (default: False)

EXAMPLES:

sage: P.<x0, x1, x2, x3> = BooleanPolynomialRing(4)
sage: I = P.ideal(x0*x1*x2*x3 + x0*x1*x3 + x0*x1 + x0*x2 + x0)
sage: I.groebner_basis()
[x0*x1 + x0*x2 + x0, x0*x2*x3 + x0*x3]

Another somewhat bigger example:

sage: sr = mq.SR(2,1,1,4,gf2=True, polybori=True)
sage: F,s = sr.polynomial_system()
sage: I = F.ideal()
sage: I.groebner_basis()
[k200 + k003, k201 + 1, k202, k203 + k003 + 1, 
 x200 + k003, x201 + k003 + 1, x202 + 1, x203, 
 w200 + k003, w201 + 1, w202 + k003 + 1, w203 + k003 + 1, 
 s100 + k003, s101 + k003 + 1, s102 + 1, s103 + 1, 
 k100, k101 + 1, k102 + k003 + 1, k103 + k003, 
 x100 + k003, x101 + 1, x102 + k003, x103 + k003, 
 w100 + 1, w101 + k003 + 1, w102, w103 + k003 + 1, 
 s000 + k003, s001 + 1, s002 + 1, s003 + k003 + 1, 
 k000, k001 + k003 + 1, k002 + 1]

TESTS:

This examples shows, that a bug in our variable indices was indeed fixed:

sage: R.<a111,a112,a121,a122,b111,b112,b211,b212,c111,c112> = BooleanPolynomialRing(order='lex')
sage: I = (a111 * b111 * c111 + a112 * b112 * c112 - 1, a111 * b211 * c111 + a112 * b212 * c112 - 0, 
...        a121 * b111 * c111 + a122 * b112 * c112, a121 * b211 * c111 + a122 * b212 * c112 - 1)*R
sage: I.groebner_basis()
[a111 + b212, a112 + b211, a121 + b112, a122 + b111, b111*b112 + b111 + b112 + 1, 
 b111*b211 + b111 + b211 + 1, b111*b212 + b112*b211 + 1, b112*b212 + b112 + b212 + 1, 
 b211*b212 + b211 + b212 + 1, c111 + 1, c112 + 1]

interreduced_basis()

If this ideal is spanned by (f_1, ..., f_n) this method returns (g_1, ..., g_s) such that:

• (f_1,...,f_n) = (g_1,...,g_s)
• LT(g_i) != LT(g_j) for all i != j`
• LT(g_i) does not divide m for all monomials m of {g_1,...,g_{i-1},g_{i+1},...,g_s}

EXAMPLE:

sage: sr = mq.SR(1, 1, 1, 4, gf2=True, polybori=True)
sage: F,s = sr.polynomial_system()
sage: I = F.ideal()
sage: I.interreduced_basis()
[k100 + k003 + 1, 
 k101 + k003, 
 k102, 
 k103 + k003, 
 x100 + 1, 
 x101 + 1, 
 x102 + 1, 
 x103 + k003, 
 w100 + k003, 
 w101, 
 w102 + k003 + 1, 
 w103 + k003 + 1, 
 s000 + 1, 
 s001 + 1, 
 s002 + 1, 
 s003 + k003 + 1, 
 k000 + k003 + 1, 
 k001, 
 k002 + k003]

reduce(f)

Reduce an element modulo the reduced Groebner basis for this ideal. This returns 0 if and only if the element is in this ideal. In any case, this reduction is unique up to monomial orders.

EXAMPLE:

sage: P = PolynomialRing(GF(2),10, 'x')
sage: B = BooleanPolynomialRing(10,'x')
sage: I = sage.rings.ideal.Cyclic(P)
sage: I = B.ideal([B(f) for f in I.gens()])
sage: gb = I.groebner_basis()
sage: I.reduce(gb[0])
0
sage: I.reduce(gb[0] + 1)
1
sage: I.reduce(gb[0]*gb[1])
0
sage: I.reduce(gb[0]*B.gen(1))
0

class sage.rings.polynomial.pbori.BooleanPolynomialIterator

Bases: object

Iterator over the monomials of a boolean polynomial.

next()

x.next() -> the next value, or raise StopIteration

class sage.rings.polynomial.pbori.BooleanPolynomialRing

Bases: sage.rings.polynomial.multi_polynomial_ring_generic.MPolynomialRing_generic

Construct a boolean polynomial ring with the following parameters:

INPUT:

• n - number of variables (an integer > 1)
• names - names of ring variables, may be a string or list/tuple
• order - term order (default: lex)

EXAMPLES:

sage: R.<x, y, z> = BooleanPolynomialRing()
sage: R
Boolean PolynomialRing in x, y, z

sage: p = x*y + x*z + y*z
sage: x*p
x*y*z + x*y + x*z

sage: R.term_order()
Lexicographic term order

sage: R = BooleanPolynomialRing(5,'x',order='deglex(3),deglex(2)')
sage: R.term_order()
deglex(3),deglex(2) term order

sage: R = BooleanPolynomialRing(3,'x',order='degrevlex')
sage: R.term_order()
Degree reverse lexicographic term order

TESTS:

sage: P.<x,y> = BooleanPolynomialRing(2,order='degrevlex')
sage: x > y
True

sage: P.<x0, x1, x2, x3> = BooleanPolynomialRing(4,order='degrevlex(2),degrevlex(2)')
sage: x0 > x1
True
sage: x2 > x3
True

clone()

Deep copy this boolean polynomial ring.

EXAMPLE:

sage: B.<a,b,c> = BooleanPolynomialRing()
sage: B.clone()
Boolean PolynomialRing in a, b, c

Note

This is part of PolyBoRi’s native interace.

cover_ring()

Return if x_1,x_2,...,x_n is the ordered list of variable names of this ring. R also has the same term ordering as this ring.

EXAMPLE:

sage: B.<x,y> = BooleanPolynomialRing(2)
sage: R = B.cover_ring(); R
Multivariate Polynomial Ring in x, y over Finite Field of size 2

sage: B.term_order() == R.term_order()
True

The cover ring is cached:

sage: B.cover_ring() is B.cover_ring()
True

defining_ideal()

Return 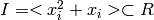where R = self.cover_ring(), and 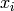any element in the set of variables of this ring.

EXAMPLE:

sage: B.<x,y> = BooleanPolynomialRing(2)
sage: I = B.defining_ideal(); I
Ideal (x^2 + x, y^2 + y) of Multivariate Polynomial Ring
in x, y over Finite Field of size 2

gen(i=0)

Returns the i-th generator of this boolean polynomial ring.

INPUT:

• i - an integer or a boolean monomial in one variable

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: P.gen()
x
sage: P.gen(2)
z
sage: m = x.monomials()[0]
sage: P.gen(m)
x

TESTS:

sage: P.<x,y,z> = BooleanPolynomialRing(3, order='dp')
sage: P.gen(0)
x

gens()

Return the tuple of variables in this ring.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: P.gens()
(x, y, z)

sage: P = BooleanPolynomialRing(10,'x')
sage: P.gens()
(x0, x1, x2, x3, x4, x5, x6, x7, x8, x9)

TESTS:

sage: P.<x,y,z> = BooleanPolynomialRing(3,order='degrevlex')
sage: P.gens()
(x, y, z)

ideal(*gens, **kwds)

Create an ideal in this ring.

INPUT:

• gens - list or tuple of generators
• coerce - bool (default: True) automatically coerce the given polynomials to this ring to form the ideal

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: P.ideal(x+y)
Ideal (x + y) of Boolean PolynomialRing in x, y, z

sage: P.ideal(x*y, y*z)
Ideal (x*y, y*z) of Boolean PolynomialRing in x, y, z

sage: P.ideal([x+y, z])
Ideal (x + y, z) of Boolean PolynomialRing in x, y, z

interpolation_polynomial(zeros, ones)

Return the lexicographically minimal boolean polynomial for the given sets of points.

Given two sets of points zeros - evaluating to zero - and ones - evaluating to one -, compute the lexicographically minimal boolean polynomial satisfying these points.

INPUT:

• zeros - the set of interpolation points mapped to zero
• ones - the set of interpolation points mapped to one

EXAMPLE:

First we create a random-ish boolean polynomial.

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing(6)
sage: f = a*b*c*e + a*d*e + a*f + b + c + e + f + 1

Now we find interpolation points mapping to zero and to one.

sage: zeros = set([(1, 0, 1, 0, 0, 0), (1, 0, 0, 0, 1, 0), \
                    (0, 0, 1, 1, 1, 1), (1, 0, 1, 1, 1, 1), \
                    (0, 0, 0, 0, 1, 0), (0, 1, 1, 1, 1, 0), \
                    (1, 1, 0, 0, 0, 1), (1, 1, 0, 1, 0, 1)])
sage: ones = set([(0, 0, 0, 0, 0, 0), (1, 0, 1, 0, 1, 0), \
                  (0, 0, 0, 1, 1, 1), (1, 0, 0, 1, 0, 1), \
                  (0, 0, 0, 0, 1, 1), (0, 1, 1, 0, 1, 1), \
                  (0, 1, 1, 1, 1, 1), (1, 1, 1, 0, 1, 0)])
sage: [f(*p) for p in zeros]
[0, 0, 0, 0, 0, 0, 0, 0]
sage: [f(*p) for p in ones]
[1, 1, 1, 1, 1, 1, 1, 1]

Finally, we find the lexicographically smallest interpolation polynomial using PolyBoRi .

sage: g = B.interpolation_polynomial(zeros, ones); g
b*f + c + d*f + d + e*f + e + 1

sage: [g(*p) for p in zeros]
[0, 0, 0, 0, 0, 0, 0, 0]
sage: [g(*p) for p in ones]
[1, 1, 1, 1, 1, 1, 1, 1]

Alternatively, we can work with PolyBoRi’s native BooleSet‘s. This example is from the PolyBoRi tutorial:

sage: B = BooleanPolynomialRing(4,"x0,x1,x2,x3")
sage: x = B.gen
sage: V=(x(0)+x(1)+x(2)+x(3)+1).set(); V
{{x0}, {x1}, {x2}, {x3}, {}}
sage: f=x(0)*x(1)+x(1)+x(2)+1
sage: z = f.zeros_in(V); z
{{x1}, {x2}}
sage: o = V.diff(z); o
{{x0}, {x3}, {}}
sage: B.interpolation_polynomial(z,o)
x1 + x2 + 1

ALGORITHM: Calls interpolate_smallest_lex as described in the PolyBoRi tutorial.

n_variables()

Returns the number of variables in this boolean polynomial ring.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: P.n_variables()
2

sage: P = BooleanPolynomialRing(1000, 'x')
sage: P.n_variables()
1000

Note

This is part of PolyBoRi’s native interace.

ngens()

Returns the number of variables in this boolean polynomial ring.

EXAMPLES:

sage: P.<x,y> = BooleanPolynomialRing(2)
sage: P.ngens()
2

sage: P = BooleanPolynomialRing(1000, 'x')
sage: P.ngens()
1000

one()

EXAMPLES:

sage: P.<x0,x1> = BooleanPolynomialRing(2)
sage: P.one()
1

random_element(degree=2, terms=5, choose_degree=True, vars_set=None)

Return a random boolean polynomial. Generated polynomial has the given number of terms, and at most given degree.

INPUT:

• degree - maximum degree (default: 2)
• terms - number of terms (default: 5)
• choose_degree - choose degree of monomials randomly first, rather than monomials uniformly random
• vars_set - list of integer indicies of generators of self to use in the generated polynomial

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: P.random_element(degree=3, terms=4)
x*y*z + x*z + y*z + z

sage: P.random_element(degree=1, terms=2)
z + 1

TESTS:

sage: P.random_element(degree=4)
...
ValueError: Given degree should be less than or equal to number of variables (3)

sage: t = P.random_element(degree=1, terms=5)
...
ValueError: Cannot generate random polynomial with 5 terms and maximum degree 1 using 3 variables

sage: t = P.random_element(degree=2,terms=5,vars_set=(0,1))
...
ValueError: Cannot generate random polynomial with 5 terms using 2 variables

set()

Sets this ring to be the active ring.

Note

This is part of PolyBoRi’s native interace.

var(i=0)

Returns the i-th generator of this boolean polynomial ring.

INPUT:

• i - an integer or a boolean monomial in one variable

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: P.var()
x
sage: P.var(2)
z
sage: m = x.monomials()[0]
sage: P.var(m)
x

TESTS:

sage: P.<x,y,z> = BooleanPolynomialRing(3, order='dp')
sage: P.var(0)
x

zero()

EXAMPLES:

sage: P.<x0,x1> = BooleanPolynomialRing(2)
sage: P.zero()
0

class sage.rings.polynomial.pbori.BooleanPolynomialVector

Bases: object

A vector of boolean polynomials.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import BooleanPolynomialVector
sage: l = [B.random_element() for _ in range(3)]
sage: v = BooleanPolynomialVector(l)
sage: len(v)
3
sage: v[0]
a*b + a*d + a + d + e
sage: list(v)
[a*b + a*d + a + d + e, a*e + a + c*f + d*f + 1, b*c + c*f + d*f + e + 1]

append(el)

Append the element el to this vector.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import BooleanPolynomialVector
sage: v = BooleanPolynomialVector()
sage: for i in range(5):
...     v.append(B.random_element())

sage: list(v)
[a*b + a*d + a + d + e, 
 a*e + a + c*f + d*f + 1, 
 b*c + c*f + d*f + e + 1, 
 a*e + a + c*f + d*f + 1, 
 b*e + d + e*f + f + 1]

class sage.rings.polynomial.pbori.BooleanPolynomialVectorIterator

Bases: object

next()

x.next() -> the next value, or raise StopIteration

class sage.rings.polynomial.pbori.CCuddNavigator

Bases: object

constant()

else_branch()

terminal_one()

then_branch()

value()

class sage.rings.polynomial.pbori.FGLMStrategy

Bases: object

Strategy object for the FGLM algorithm to translate from one Groebner basis with respect to a term ordering A to another Groebner basis with respect to a term ordering B.

main()

Execute the FGLM algorithm.

EXAMPLE:

sage: from polybori import *                                  
sage: B.<x,y,z> = BooleanPolynomialRing()
sage: x > y > z                                               
True                                                          
sage: old_ring  = B
sage: change_ordering(dp_asc)                                 
sage: x > y > z                           
False                                           
sage: z > y > x
True
sage: new_ring = global_ring()
sage: ideal = BooleanPolynomialVector([x+z, y+z])
sage: list(FGLMStrategy(old_ring, new_ring, ideal).main())
[y + x, z + x]

class sage.rings.polynomial.pbori.GroebnerStrategy

Bases: object

A Groebner strategy is the main object to control the strategy for computing Groebner bases.

Note

This class is mainly used internally.

add_as_you_wish(p)

Add a new generator but let the strategy object decide whether to perform immediate interreduction.

INPUT:

• p - a polynomial

EXAMPLE:

sage: from polybori import *
sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: gbs = GroebnerStrategy()
sage: gbs.add_as_you_wish(a + b)
sage: list(gbs)
[a + b]
sage: gbs.add_as_you_wish(a + c)

Note that nothing happened immediatly but that the generator was indeed added:

sage: list(gbs)
[a + b]

sage: gbs.symmGB_F2()
sage: list(gbs)
[a + c, b + c]

add_generator(p)

Add a new generator.

INPUT:

• p - a polynomial

EXAMPLE:

sage: from polybori import *
sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: gbs = GroebnerStrategy()
sage: gbs.add_generator(a + b)
sage: list(gbs)
[a + b]
sage: gbs.add_generator(a + c)
...
ValueError: strategy already contains a polynomial with same lead

add_generator_delayed(p)

Add a new generator but do not perform interreduction immediatly.

INPUT:

• p - a polynomial

EXAMPLE:

sage: from polybori import *
sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: gbs = GroebnerStrategy()
sage: gbs.add_generator(a + b)
sage: list(gbs)
[a + b]
sage: gbs.add_generator_delayed(a + c)
sage: list(gbs)
[a + b]

sage: list(gbs.all_generators())
[a + b, a + c]

all_generators()

EXAMPLE:

sage: from polybori import *
sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: gbs = GroebnerStrategy()
sage: gbs.add_as_you_wish(a + b)
sage: list(gbs)
[a + b]
sage: gbs.add_as_you_wish(a + c)

sage: list(gbs)
[a + b]

sage: list(gbs.all_generators())
[a + b, a + c]

all_spolys_in_next_degree()

clean_top_by_chain_criterion()

contains_one()

Return True if 1 is in the generating system.

EXAMPLE:

We construct an example which contains 1 in the ideal spanned by the generators but not in the set of generators:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import GroebnerStrategy
sage: gb = GroebnerStrategy()
sage: gb.add_generator(a*c + a*f + d*f + d + f)
sage: gb.add_generator(b*c + b*e + c + d + 1)
sage: gb.add_generator(a*f + a + c + d + 1)
sage: gb.add_generator(a*d + a*e + b*e + c + f)
sage: gb.add_generator(b*d + c + d*f + e + f)
sage: gb.add_generator(a*b + b + c*e + e + 1)
sage: gb.add_generator(a + b + c*d + c*e + 1)
sage: gb.contains_one()
False

Still, we have that:

sage: from polybori import groebner_basis
sage: groebner_basis(gb)
[1]

faugere_step_dense(v)

Reduces a vector of polynomials using linear algebra.

INPUT:

• v - a boolean polynomial vector

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import GroebnerStrategy
sage: gb = GroebnerStrategy()
sage: gb.add_generator(a*c + a*f + d*f + d + f)
sage: gb.add_generator(b*c + b*e + c + d + 1)
sage: gb.add_generator(a*f + a + c + d + 1)
sage: gb.add_generator(a*d + a*e + b*e + c + f)
sage: gb.add_generator(b*d + c + d*f + e + f)
sage: gb.add_generator(a*b + b + c*e + e + 1)
sage: gb.add_generator(a + b + c*d + c*e + 1)

sage: from polybori import BooleanPolynomialVector
sage: V= BooleanPolynomialVector([b*d, a*b])
sage: list(gb.faugere_step_dense(V))
[b + c*e + e + 1, c + d*f + e + f]

implications(i)

Compute “useful” implied polynomials of i-th generator, and add them to the strategy, if it finds any.

INPUT:

• i - an index

ll_reduce_all()

Use the built-in ll-encoded BooleSet of polynomials with linear lexicographical leading term, which coincides with leading term in current ordering, to reduce the tails of all polynomials in the strategy.

minimalize()

Return a vector of all polynomials with minimal leading terms.

Note

Use this function if strat contains a GB.

minimalize_and_tail_reduce()

Return a vector of all polynomials with minimal leading terms and do tail reductions.

Note

Use that if strat contains a GB and you want a reduced GB.

next_spoly()

nf(p)

Compute the normal form of p with respect to the generating set.

INPUT:

• p - a boolean polynomial

EXAMPLE:

sage: P = PolynomialRing(GF(2),10, 'x')
sage: B = BooleanPolynomialRing(10,'x')
sage: I = sage.rings.ideal.Cyclic(P)
sage: I = B.ideal([B(f) for f in I.gens()])
sage: gb = I.groebner_basis()

sage: from polybori import GroebnerStrategy

sage: G = GroebnerStrategy()
sage: _ = [G.add_generator(f) for f in gb]
sage: G.nf(gb[0])
0
sage: G.nf(gb[0] + 1)
1
sage: G.nf(gb[0]*gb[1])
0
sage: G.nf(gb[0]*B.gen(1))
0

Note

The result is only canonical if the generating set is a Groebner basis.

npairs()

reduction_strategy

select(m)

Return the index of the generator which can reduce the monomial m.

INPUT:

• m - a BooleanMonomial

EXAMPLE:

sage: B.<a,b,c,d,e> = BooleanPolynomialRing()
sage: f = B.random_element()                       
sage: g = B.random_element()
sage: from polybori import GroebnerStrategy
sage: strat = GroebnerStrategy()
sage: strat.add_generator(f)          
sage: strat.add_generator(g)
sage: strat.select(f.lm())
0
sage: strat.select(g.lm())
1
sage: strat.select(e.lm())
-1

small_spolys_in_next_degree(f, n)

some_spolys_in_next_degree(n)

suggest_plugin_variable()

symmGB_F2()

Compute a Groebner basis for the generating system.

Note

This implementation is out of date, but it will revived at some point in time. Use the groebner_basis() function instead.

top_sugar()

variable_has_value(v)

Computes, whether there exists some polynomial of the form 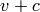in the Strategy – where c is a constant – in the list of generators.

INPUT:

• v - the index of a variable

EXAMPLE::

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing() sage: from polybori import GroebnerStrategy sage: gb = GroebnerStrategy() sage: gb.add_generator(a*c + a*f + d*f + d + f) sage: gb.add_generator(b*c + b*e + c + d + 1) sage: gb.add_generator(a*f + a + c + d + 1) sage: gb.add_generator(a*d + a*e + b*e + c + f) sage: gb.add_generator(b*d + c + d*f + e + f) sage: gb.add_generator(a*b + b + c*e + e + 1) sage: gb.variable_has_value(0) False

sage: from polybori import groebner_basis sage: g = groebner_basis(gb) sage: list(g) [a, b + 1, c + 1, d, e + 1, f]

sage: gb = GroebnerStrategy() sage: _ = [gb.add_generator(f) for f in g] sage: gb.variable_has_value(0) True

class sage.rings.polynomial.pbori.MonomialFactory

Bases: object

Implements PolyBoRi’s Monomial() constructor.

class sage.rings.polynomial.pbori.PolynomialFactory

Bases: object

Implements PolyBoRi’s Polynomial() constructor.

lead(x)

Return the leading monomial of boolean polynomial x, with respect to to the order of parent ring.

EXAMPLE:

sage: from polybori import *
sage: B.<a,b,c> = BooleanPolynomialRing()
sage: PolynomialFactory().lead(a)
a

class sage.rings.polynomial.pbori.ReductionStrategy

Bases: object

Functions and options for boolean polynomial reduction.

add_generator(p)

Add the new generator p to this strategy.

INPUT:

• p - a boolean polynomial.

EXAMPLE:

sage: from polybori import *
sage: B.<x,y,z> = BooleanPolynomialRing()
sage: red = ReductionStrategy()
sage: red.add_generator(x)
sage: list([f.p for f in red])
[x]

TESTS:

Check if #8966 is fixed:

sage: red = ReductionStrategy()
sage: red.add_generator(None)
...
TypeError: argument must be a BooleanPolynomial.

can_rewrite(p)

Return True if p can be reduced by the generators of this strategy.

EXAMPLE:

sage: from polybori import *
sage: B.<a,b,c,d> = BooleanPolynomialRing()
sage: red = ReductionStrategy()
sage: red.add_generator(a*b + c + 1)
sage: red.add_generator(b*c + d + 1)
sage: red.can_rewrite(a*b + a)
True
sage: red.can_rewrite(b + c)
False
sage: red.can_rewrite(a*d + b*c + d + 1)
True

head_normal_form(p)

Compute the normal form of p with respect to the generators of this strategy but do not perform tail any reductions.

INPUT:

• p - a polynomial

EXAMPLE:

sage: from polybori import *
sage: B.<x,y,z> = BooleanPolynomialRing()
sage: red = ReductionStrategy()
sage: red.opt_red_tail = True
sage: red.add_generator(x + y + 1)
sage: red.add_generator(y*z + z)

sage: red.head_normal_form(x + y*z)
y + z + 1

sage; red.nf(x + y*z)
y + z + 1

nf(p)

Compute the normal form of p w.r.t. to the generators of this reduction strategy object.

EXAMPLE:

sage: from polybori import *
sage: B.<x,y,z> = BooleanPolynomialRing()
sage: red = ReductionStrategy()
sage: red.add_generator(x + y + 1)
sage: red.add_generator(y*z + z)
sage: red.nf(x)
y + 1

sage: red.nf(y*z + x)
y + z + 1

reduced_normal_form(p)

Compute the normal form of p with respect to the generators of this strategy and perform tail reductions.

INPUT:

• p - a polynomial

EXAMPLE:

sage: from polybori import *
sage: B.<x,y,z> = BooleanPolynomialRing()
sage: red = ReductionStrategy()
sage: red.add_generator(x + y + 1)
sage: red.add_generator(y*z + z)
sage: red.reduced_normal_form(x)
y + 1

sage: red.reduced_normal_form(y*z + x)
y + z + 1

sage.rings.polynomial.pbori.VariableBlock(size, start_index, offset, reverse)

class sage.rings.polynomial.pbori.VariableBlockFalse

Bases: sage.rings.polynomial.pbori.VariableBlock_base

class sage.rings.polynomial.pbori.VariableBlockTrue

Bases: sage.rings.polynomial.pbori.VariableBlock_base

class sage.rings.polynomial.pbori.VariableBlock_base

Bases: object

class sage.rings.polynomial.pbori.VariableFactory

Bases: object

Implements PolyBoRi’s Variable() constructor.

sage.rings.polynomial.pbori.add_cring(R)

Add the ring R to the list of rings for which we keep track if there exists a PolyBoRi C++ ring.

EXAMPLE:

sage: from polybori import add_cring
sage: B = BooleanPolynomialRing(1000,'x')
sage: add_cring(B)

sage.rings.polynomial.pbori.add_up_polynomials(v)

Add up all entries in the vector v.

INPUT:

• v - a vector of boolean polynomials

EXAMPLE:

sage: from polybori import *
sage: B.<a,b,c,d> = BooleanPolynomialRing()
sage: v = BooleanPolynomialVector()
sage: l = [B.random_element() for _ in range(5)]
sage: _ = [v.append(e) for e in l]
sage: add_up_polynomials(v)
a*c + a*d + b*c + b*d + c*d + c + 1
sage: sum(l)
a*c + a*d + b*c + b*d + c*d + c + 1

sage.rings.polynomial.pbori.append_ring_block(i)

sage.rings.polynomial.pbori.change_ordering(order)

Return True if the current global ring has a degree order.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import have_degree_order, change_ordering
sage: have_degree_order()
False
sage: change_ordering(1)
sage: have_degree_order()
True

Note

Sage assumes that rings are immutable. This function which is part of the PolyBoRi upstream API does not follow this rule.

sage.rings.polynomial.pbori.contained_vars(m)

sage.rings.polynomial.pbori.easy_linear_factors(p)

sage.rings.polynomial.pbori.gauss_on_polys(inp)

Perform Gaussian elimination on the input list of polynomials.

INPUT:

• inp - an iterable

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import *
sage: l = [B.random_element() for _ in range(B.ngens())]
sage: A,v = mq.MPolynomialSystem(B,l).coefficient_matrix()
sage: A
[1 0 1 0 1 0 0 0 0 1 0 1 0 0]                                                                   
[0 0 0 1 1 0 0 1 1 0 0 0 0 1]                                                                   
[0 0 0 0 0 1 0 1 1 0 0 1 0 1]                                                                   
[0 0 0 1 1 0 0 1 1 0 0 0 0 1]                                                                   
[0 0 0 0 0 0 1 0 0 1 1 0 1 1]                                                                   
[0 1 1 0 0 0 0 0 0 0 0 1 1 1]   

sage: e = gauss_on_polys(l)
sage: E,v = mq.MPolynomialSystem(B,e).coefficient_matrix()
sage: E
[1 0 1 0 1 0 0 0 0 1 0 1 0 0]                                                                   
[0 1 1 0 0 0 0 0 0 0 0 1 1 1]                                                                   
[0 0 0 1 1 0 0 1 1 0 0 0 0 1]                                                                   
[0 0 0 0 0 1 0 1 1 0 0 1 0 1]                                                                   
[0 0 0 0 0 0 1 0 0 1 1 0 1 1] 

sage: A.echelon_form()
[1 0 1 0 1 0 0 0 0 1 0 1 0 0]
[0 1 1 0 0 0 0 0 0 0 0 1 1 1]
[0 0 0 1 1 0 0 1 1 0 0 0 0 1]
[0 0 0 0 0 1 0 1 1 0 0 1 0 1]
[0 0 0 0 0 0 1 0 0 1 1 0 1 1]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0]

sage.rings.polynomial.pbori.get_cring()

Return the currently active global ring, this is only relevant for the native PolyBoRi interface.

EXAMPLE:

sage: from polybori import declare_ring, get_cring, Block
sage: R = declare_ring([Block('x',2),Block('y',3)],globals())
sage: Q = get_cring(); Q
Boolean PolynomialRing in x(0), x(1), y(0), y(1), y(2)
sage: R is Q
True


sage: from polybori import *
sage: B = BooleanPolynomialRing(10,'x',order='lex')
sage: change_ordering(block_dp_asc)
sage: append_ring_block(5)
sage: get_cring().term_order()
deglex_asc(5),deglex_asc(5) term order

sage.rings.polynomial.pbori.get_order_code()

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import get_order_code
sage: get_order_code()
0

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing(order='deglex')
sage: get_order_code()
1

Note

This function which is part of the PolyBoRi upstream API works with a current global ring. This notion is avoided in Sage.

sage.rings.polynomial.pbori.get_var_mapping(ring, other)

Return a variable mapping between variables of other and ring. When other is a parent object, the mapping defines images for all variables of other. If it is an element, only variables occurring in other are mapped.

Raises NameError if no such mapping is possible.

EXAMPLES:

sage: P.<x,y,z> = BooleanPolynomialRing(3)
sage: R.<z,y> = QQ[]
sage: sage.rings.polynomial.pbori.get_var_mapping(P,R)
[z, y]
sage: sage.rings.polynomial.pbori.get_var_mapping(P, z^2)
[z, None]

sage: R.<z,x> = BooleanPolynomialRing(2)
sage: sage.rings.polynomial.pbori.get_var_mapping(P,R)
[z, x]
sage: sage.rings.polynomial.pbori.get_var_mapping(P, x^2)
[None, x]

sage.rings.polynomial.pbori.have_degree_order()

Return True if the current global ring has a degree order.

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import have_degree_order
sage: have_degree_order()
False
sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing(order='deglex')
sage: have_degree_order()
True

Note

This function is only relevant for the upstream PolyBoRi API. In Sage the notion of a current global ring is avoided.

sage.rings.polynomial.pbori.if_then_else(root, a, b)

The opposite of navigating down a ZDD using navigators is to construct new ZDDs in the same way, namely giving their else- and then-branch as well as the index value of the new node.

INPUT:

• root - a variable
• a - the if branch, a BooleSet or a BoolePolynomial
• b - the else branch, a BooleSet or a BoolePolynomial

EXAMPLE:

sage: from polybori import if_then_else
sage: B = BooleanPolynomialRing(6,'x')
sage: x0,x1,x2,x3,x4,x5 = B.gens()
sage: f0 = x2*x3+x3
sage: f1 = x4
sage: if_then_else(x1, f0, f1)
{{x1,x2,x3}, {x1,x3}, {x4}}

sage: if_then_else(x1.lm().index(),f0,f1)
{{x1,x2,x3}, {x1,x3}, {x4}}

sage: if_then_else(x5, f0, f1)
...
IndexError: index of root must be less than the values of roots of the branches.

sage.rings.polynomial.pbori.interpolate(zero, one)

Interpolate a polynomial evaluating to zero on zero and to one on ones.

INPUT:

• zero - the set of zero
• one - the set of ones

EXAMPLE:

sage: B = BooleanPolynomialRing(4,"x0,x1,x2,x3")
sage: x = B.gen
sage: from polybori.interpolate import *
sage: V=(x(0)+x(1)+x(2)+x(3)+1).set() 

sage: V 
{{x0}, {x1}, {x2}, {x3}, {}} 

sage: f=x(0)*x(1)+x(1)+x(2)+1 
sage: nf_lex_points(f,V) 
x1 + x2 + 1 

sage: z=f.zeros_in(V) 
sage: z 
{{x1}, {x2}} 

sage: o=V.diff(z) 
sage: o 
{{x0}, {x3}, {}} 

sage: interpolate(z,o) 
x0*x1*x2 + x0*x1 + x0*x2 + x1*x2 + x1 + x2 + 1

sage.rings.polynomial.pbori.interpolate_smallest_lex(zero, one)

Interpolate the lexicographical smallest polynomial evaluating to zero on zero and to one on ones.

INPUT:

• zero - the set of zeros
• one - the set of ones

EXAMPLE:

Let V be a set of points in 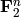and f a Boolean polynomial. V can be encoded as a BooleSet. Then we are interested in the normal form of f against the vanishing ideal of V : I(V).

It turns out, that the computation of the normal form can be done by the computation of a minimal interpolation polynomial, which takes the same values as f on V:

sage: B = BooleanPolynomialRing(4,"x0,x1,x2,x3")
sage: x = B.gen
sage: from polybori.interpolate import *
sage: V=(x(0)+x(1)+x(2)+x(3)+1).set() 

We take V = {e0,e1,e2,e3,0}, where ei describes the i-th unit vector. For our considerations it does not play any role, if we suppose V to be embedded in 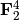or a vector space of higher dimension:

sage: V 
{{x0}, {x1}, {x2}, {x3}, {}} 

sage: f=x(0)*x(1)+x(1)+x(2)+1 
sage: nf_lex_points(f,V) 
x1 + x2 + 1 

In this case, the normal form of f w.r.t. the vanishing ideal of V consists of all terms of f with degree smaller or equal to 1.

It can be easily seen, that this polynomial forms the same function on V as f. In fact, our computation is equivalent to the direct call of the interpolation function interpolate_smallest_lex, which has two arguments: the set of interpolation points mapped to zero and the set of interpolation points mapped to one:

sage: z=f.zeros_in(V) 
sage: z 
{{x1}, {x2}} 

sage: o=V.diff(z) 
sage: o 
{{x0}, {x3}, {}} 

sage: interpolate_smallest_lex(z,o) 
x1 + x2 + 1

sage.rings.polynomial.pbori.ll_red_nf_noredsb(p, reductors)

Redude the polynomial p by the set of reductors with linear leading terms.

INPUT:

• p - a boolean polynomial
• reductors - a boolean set encoding a Groebner basis with linear leading terms.

EXAMPLE:

sage: from polybori import ll_red_nf_noredsb
sage: B.<a,b,c,d> = BooleanPolynomialRing()
sage: p = a*b + c + d + 1
sage: f,g  = a + c + 1, b + d + 1;
sage: reductors = f.set().union( g.set() )
sage: ll_red_nf_noredsb(p, reductors)
b*c + b*d + c + d + 1

sage.rings.polynomial.pbori.ll_red_nf_noredsb_single_recursive_call(p, reductors)

Redude the polynomial p by the set of reductors with linear leading terms.

ll_red_nf_noredsb_single_recursive() call has the same specification as ll_red_nf_noredsb(), but a different implementation: It is very sensitive to the ordering of variables, however it has the property, that it needs just one recursive call.

INPUT:

• p - a boolean polynomial
• reductors - a boolean set encoding a Groebner basis with linear leading terms.

EXAMPLE:

sage: from polybori import ll_red_nf_noredsb_single_recursive_call
sage: B.<a,b,c,d> = BooleanPolynomialRing()
sage: p = a*b + c + d + 1
sage: f,g  = a + c + 1, b + d + 1;
sage: reductors = f.set().union( g.set() )
sage: ll_red_nf_noredsb_single_recursive_call(p, reductors)
b*c + b*d + c + d + 1

sage.rings.polynomial.pbori.ll_red_nf_redsb(p, reductors)

Redude the polynomial p by the set of reductors with linear leading terms. It is assumed that the set reductors is a reduced Groebner basis.

INPUT:

• p - a boolean polynomial
• reductors - a boolean set encoding a reduced Groebner basis with linear leading terms.

EXAMPLE:

sage: from polybori import ll_red_nf_redsb
sage: B.<a,b,c,d> = BooleanPolynomialRing()
sage: p = a*b + c + d + 1
sage: f,g  = a + c + 1, b + d + 1;
sage: reductors = f.set().union( g.set() )
sage: ll_red_nf_redsb(p, reductors)
b*c + b*d + c + d + 1

sage.rings.polynomial.pbori.map_every_x_to_x_plus_one(p)

Map every variable x_i in this polynomial to x_i + 1.

EXAMPLE:

sage: B.<a,b,z> = BooleanPolynomialRing(3)
sage: f = a*b + z + 1; f
a*b + z + 1
sage: from polybori import map_every_x_to_x_plus_one
sage: map_every_x_to_x_plus_one(f)
a*b + a + b + z + 1
sage: f(a+1,b+1,z+1)
a*b + a + b + z + 1

sage.rings.polynomial.pbori.mod_mon_set(as, vs)

sage.rings.polynomial.pbori.mod_var_set(a, v)

sage.rings.polynomial.pbori.mult_fact_sim_C(v)

sage.rings.polynomial.pbori.nf3(s, p, m)

sage.rings.polynomial.pbori.parallel_reduce(inp, strat, average_steps, delay_f)

sage.rings.polynomial.pbori.random_set(variables, length)

Return a random set of monomials with length elements with each element in the variables variables.

EXAMPLE:

sage: from polybori import random_set, set_random_seed
sage: B.<a,b,c,d,e> = BooleanPolynomialRing()
sage: (a*b*c*d).lm()
a*b*c*d
sage: set_random_seed(1337)
sage: random_set((a*b*c*d).lm(),10)
{{a,b,c,d}, {a,b,d}, {a,c}, {a,d}, {a}, {b,c}, {b}, {c,d}, {c}, {}}

sage.rings.polynomial.pbori.recursively_insert(n, ind, m)

sage.rings.polynomial.pbori.red_tail(s, p)

Perform tail reduction on p using the generators of s.

INPUT:

• s - a reduction strategy
• p - a polynomial

EXAMPLE:

sage: from polybori import *
sage: B.<x,y,z> = BooleanPolynomialRing()
sage: red = ReductionStrategy()
sage: red.add_generator(x + y + 1)
sage: red.add_generator(y*z + z)
sage: red_tail(red,x)
x
sage: red_tail(red,x*y + x)
x*y + y + 1

sage.rings.polynomial.pbori.set_cring(R)

Set the currently active global ring, this is only relevant for the native PolyBoRi interface.

sage: from polybori import *
sage: declare_ring([Block('x',2),Block('y',3)],globals())
Boolean PolynomialRing in x(0), x(1), y(0), y(1), y(2)
sage: R = get_cring(); R
Boolean PolynomialRing in x(0), x(1), y(0), y(1), y(2)

sage: declare_ring([Block('x',2),Block('y',2)],globals())
Boolean PolynomialRing in x(0), x(1), y(0), y(1)

sage: get_cring()
Boolean PolynomialRing in x(0), x(1), y(0), y(1)

sage: set_cring(R)
sage: get_cring()
Boolean PolynomialRing in x(0), x(1), y(0), y(1), y(2)

sage.rings.polynomial.pbori.set_random_seed(seed)

The the PolyBoRi random seed to seed

EXAMPLE:

sage: from polybori import random_set, set_random_seed
sage: B.<a,b,c,d,e> = BooleanPolynomialRing()
sage: (a*b*c*d).lm()
a*b*c*d
sage: set_random_seed(1337)
sage: random_set((a*b*c*d).lm(),2)
{{b,c}, {b}}
sage: random_set((a*b*c*d).lm(),2)
{{a,c}, {}}

sage: set_random_seed(1337)
sage: random_set((a*b*c*d).lm(),2)
{{b,c}, {b}}
sage: random_set((a*b*c*d).lm(),2)
{{a,c}, {}}

sage.rings.polynomial.pbori.set_variable_name(i, s)

Set the variable name for the i-th variable in the current global ring to s.

INPUT:

• i - an index
• s - a name

EXAMPLE:

sage: B.<a,b,c,d,e,f> = BooleanPolynomialRing()
sage: from polybori import set_variable_name
sage: set_variable_name(0, 'dontdothis')
sage: a
dontdothis

sage: set_variable_name(100, 'doesntwork')
...
IndexError

Note

Sage assumes that rings are immutable. This function which is part of the PolyBoRi upstream API does not follow this rule.

sage.rings.polynomial.pbori.substitute_variables(vec, poly)

var(i) is replaced by vec[i] in poly.

EXAMPLE::

sage: B.<a,b,c> = BooleanPolynomialRing() sage: f = a*b + c + 1 sage: from polybori import substitute_variables sage: substitute_variables([a,b,c],f) a*b + c + 1 sage: substitute_variables([a+1,b,c],f) a*b + b + c + 1 sage: substitute_variables([a+1,b+1,c],f) a*b + a + b + c sage: substitute_variables([a+1,b+1,B(0)],f) a*b + a + b

sage.rings.polynomial.pbori.top_index(s)

Return the highest index in the parameter s.

INPUT:

• s - BooleSet, BooleMonomial, BoolePolynomial

EXAMPLE:

sage: B.<x,y,z> = BooleanPolynomialRing(3)
sage: from polybori import top_index
sage: top_index(x.lm())
0
sage: top_index(y*z)
1
sage: top_index(x + 1)
0

sage.rings.polynomial.pbori.unpickle_BooleanPolynomial(ring, string)

Unpickle boolean polynomials

EXAMPLE:

sage: T = TermOrder('deglex',2)+TermOrder('deglex',2) 
sage: P.<a,b,c,d> = BooleanPolynomialRing(4,order=T) 
sage: loads(dumps(a+b)) == a+b # indirect doctest
True

sage.rings.polynomial.pbori.unpickle_BooleanPolynomial0(ring, l)

Unpickle boolean polynomials

EXAMPLE:

sage: T = TermOrder('deglex',2)+TermOrder('deglex',2) 
sage: P.<a,b,c,d> = BooleanPolynomialRing(4,order=T) 
sage: loads(dumps(a+b)) == a+b # indirect doctest
True

sage.rings.polynomial.pbori.unpickle_BooleanPolynomialRing(n, names, order)

Unpickle boolean polynomial rings.

EXAMPLE:

sage: T = TermOrder('deglex',2)+TermOrder('deglex',2) 
sage: P.<a,b,c,d> = BooleanPolynomialRing(4,order=T) 
sage: loads(dumps(P)) == P  # indirect doctest
True

sage.rings.polynomial.pbori.zeros(pol, s)

Return a BooleSet encoding on which points from s the polynomial pol evaluates to zero.

INPUT:

• pol - a boolean polynomial
• s - a set of points encoded as a BooleSet

EXAMPLE:

sage: B.<a,b,c,d> = BooleanPolynomialRing(4)
sage: f = a*b + a*c + d + b

Now we create a set of points:

sage: s = a*b + a*b*c + c*d + b*c
sage: s = s.set(); s
{{a,b,c}, {a,b}, {b,c}, {c,d}}

This encodes the points (1,1,1,0), (1,1,0,0), (0,0,1,1) and (0,1,1,0). But of these only (1,1,0,0) evaluates to zero.:

sage: from polybori import zeros
sage: zeros(f,s)
{{a,b}}

For comparison we work with tuples:

sage: f.zeros_in([(1,1,1,0), (1,1,0,0), (0,0,1,1), (0,1,1,0)])
((1, 1, 0, 0),)