Base class for multivariate polynomial rings

class sage.rings.polynomial.multi_polynomial_ring_generic.MPolynomialRing_generic

Bases: sage.rings.ring.CommutativeRing

change_ring(base_ring=None, names=None, order=None)

Return a new multivariate polynomial ring which isomorphic to self, but has a different ordering given by the parameter ‘order’ or names given by the parameter ‘names’.

INPUT:

• base_ring – a base ring
• names – variable names
• order – a term order

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(GF(127),3,order='lex')
sage: x > y^2
True
sage: Q.<x,y,z> = P.change_ring(order='degrevlex')
sage: x > y^2
False

characteristic()

Return the characteristic of this polynomial ring.

EXAMPLES:

sage: R = PolynomialRing(QQ, 'x', 3)
sage: R.characteristic()
0
sage: R = PolynomialRing(GF(7),'x', 20)
sage: R.characteristic()
7

completion(p, prec=20, extras=None)

construction()

Returns a functor F and base ring R such that F(R) == self.

EXAMPLES:

sage: S = ZZ['x,y']
sage: F, R = S.construction(); R
Integer Ring
sage: F
MPoly[x,y]
sage: F(R) == S
True
sage: F(R) == ZZ['x']['y']
False

gen(n=0)

irrelevant_ideal()

Return the irrelevant ideal of this multivariate polynomial ring, which is the ideal generated by all of the indeterminate generators of this ring.

EXAMPLES:

sage: R.<x,y,z> = QQ[]
sage: R.irrelevant_ideal()
Ideal (x, y, z) of Multivariate Polynomial Ring in x, y, z over Rational Field

is_field(proof=True)

Return True if this multivariate polynomial ring is a field, i.e., it is a ring in 0 generators over a field.

is_finite()

is_integral_domain(proof=True)

EXAMPLES:

sage: ZZ['x,y'].is_integral_domain()
True
sage: Integers(8)['x,y'].is_integral_domain()
False

is_noetherian()

EXAMPLES:

sage: ZZ['x,y'].is_noetherian()
True
sage: Integers(8)['x,y'].is_noetherian()
True

krull_dimension()

ngens()

random_element(degree, terms, choose_degree=2, *args=None, **kwargs=False)

Return a random polynomial of at most degree and at most terms.

First monomials are chosen uniformly random from the set of all possible monomials of degree up to (inclusive). This means that it is more likely that a monomial of degree appears than a monomial of degree 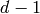because the former class is bigger.

Exactly distinct monomials are chosen this way and each one gets a random coefficient (possibly zero) from the base ring assigned.

The returned polynomial is the sum of this list of terms.

INPUT:

• degree – maximal degree (likely to be reached) (default: 2)
• terms – number of terms requested (default: 5)
• choose_degree – choose degrees of monomials randomly first rather than monomials uniformly random.
• **kwargs – passed to the random element generator of the base ring

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ)
sage: P.random_element(2, 5)
-6/5*x^2 + 2/3*z^2 - 1

sage: P.random_element(2, 5, choose_degree=True)
-1/4*x*y - 1/5*x*z - 1/14*y*z - z^2

Stacked rings:

sage: R = QQ['x,y']
sage: S = R['t,u']
sage: S.random_element(degree=2, terms=1)
-3*x*y + 5/2*y^2 - 1/2*x - 1/4*y + 4
sage: S.random_element(degree=2, terms=1)
(-1/2*x^2 - x*y - 2/7*y^2 + 3/2*x - y)*t*u

Default values apply if no degree and/or number of terms is provided:

sage: random_matrix(QQ['x,y,z'], 2, 2)
[        2*y^2 - 2/27*y*z - z^2 + 2*z        1/2*x*y - 1/2*y^2 + 2*x - 2*y]
[-1/27*x^2 + 2/5*y^2 - 1/10*z^2 - 2*z              -13*y^2 + 2/3*z^2 + 2*y]

sage: random_matrix(QQ['x,y,z'], 2, 2, terms=1, degree=2)
[-1/4*x    1/2]
[ 1/3*x    x*y]

sage: P.random_element(0, 1)
-1

sage: P.random_element(2, 0)
0

sage: R.<x> = PolynomialRing(Integers(3), 1)
sage: R.random_element()
x + 1

remove_var(var)

repr_long()

Return structured string representation of self.

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ,order=TermOrder('degrevlex',1)+TermOrder('lex',2))
sage: print P.repr_long()
Polynomial Ring
 Base Ring : Rational Field
      Size : 3 Variables
  Block  0 : Ordering : degrevlex
             Names    : x
  Block  1 : Ordering : lex
             Names    : y, z

term_order()

variable_names_recursive(depth='sage.rings.infinity.infinity')

Returns the list of variable names of this and its base rings, as if it were a single multi-variate polynomial.

EXAMPLES:

sage: R = QQ['x,y']['z,w']
sage: R.variable_names_recursive()
('x', 'y', 'z', 'w')
sage: R.variable_names_recursive(3)
('y', 'z', 'w')

sage.rings.polynomial.multi_polynomial_ring_generic.is_MPolynomialRing(x)

sage.rings.polynomial.multi_polynomial_ring_generic.unpickle_MPolynomialRing_generic(base_ring, n, names, order)

sage.rings.polynomial.multi_polynomial_ring_generic.unpickle_MPolynomialRing_generic_v1(base_ring, n, names, order)