Sage has a powerful system to compute with multivariate polynomial rings. Most algorithms dealing with these ideals are centered the computation of Groebner bases. Sage mainly uses Singular to implement this functionality. Singular is widely regarded as the best open-source system for Groebner basis calculation in multivariate polynomial rings over fields.
AUTHORS:
EXAMPLES:
We compute a Groebner basis for some given ideal. The type returned by the groebner_basis method is Sequence, i.e. it is not a MPolynomialIdeal:
sage: x,y,z = QQ['x,y,z'].gens()
sage: I = ideal(x^5 + y^4 + z^3 - 1, x^3 + y^3 + z^2 - 1)
sage: B = I.groebner_basis()
sage: type(B)
<class 'sage.structure.sequence.Sequence'>
Groebner bases can be used to solve the ideal membership problem:
sage: f,g,h = B
sage: (2*x*f + g).reduce(B)
0
sage: (2*x*f + g) in I
True
sage: (2*x*f + 2*z*h + y^3).reduce(B)
y^3
sage: (2*x*f + 2*z*h + y^3) in I
False
We compute a Groebner basis for Cyclic 6, which is a standard benchmark and test ideal.
sage: R.<x,y,z,t,u,v> = QQ['x,y,z,t,u,v']
sage: I = sage.rings.ideal.Cyclic(R,6)
sage: B = I.groebner_basis()
sage: len(B)
45
We compute in a quotient of a polynomial ring over 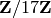 :
:
sage: R.<x,y> = ZZ[]
sage: S.<a,b> = R.quotient((x^2 + y^2, 17))
sage: S
Quotient of Multivariate Polynomial Ring in x, y over Integer Ring
by the ideal (x^2 + y^2, 17)
sage: a^2 + b^2 == 0
True
sage: a^3 - b^2
-a*b^2 - b^2
Note that the result of a computation is not necessarily reduced:
sage: (a+b)^17
256*a*b^16 + 256*b^17
sage: S(17) == 0
True
Or we can work with 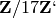 directly:
directly:
sage: R.<x,y> = Zmod(17)[]
sage: S.<a,b> = R.quotient((x^2 + y^2,))
sage: S
Quotient of Multivariate Polynomial Ring in x, y over Ring of
integers modulo 17 by the ideal (x^2 + y^2)
sage: a^2 + b^2 == 0
True
sage: a^3 - b^2
-a*b^2 - b^2
sage: (a+b)^17
a*b^16 + b^17
sage: S(17) == 0
True
Working with a polynomial ring over  :
:
sage: R.<x,y,z,w> = ZZ[]
sage: I = ideal(x^2 + y^2 - z^2 - w^2, x-y)
sage: J = I^2
sage: J.groebner_basis()
[4*y^4 - 4*y^2*z^2 + z^4 - 4*y^2*w^2 + 2*z^2*w^2 + w^4,
2*x*y^2 - 2*y^3 - x*z^2 + y*z^2 - x*w^2 + y*w^2,
x^2 - 2*x*y + y^2]
sage: y^2 - 2*x*y + x^2 in J
True
sage: 0 in J
True
We do a Groebner basis computation over a number field:
sage: K.<zeta> = CyclotomicField(3)
sage: R.<x,y,z> = K[]; R
Multivariate Polynomial Ring in x, y, z over Cyclotomic Field of order 3 and degree 2
sage: i = ideal(x - zeta*y + 1, x^3 - zeta*y^3); i
Ideal (x + (-zeta)*y + 1, x^3 + (-zeta)*y^3) of Multivariate
Polynomial Ring in x, y, z over Cyclotomic Field of order 3 and degree 2
sage: i.groebner_basis()
[y^3 + (2*zeta + 1)*y^2 + (zeta - 1)*y + (-1/3*zeta - 2/3), x + (-zeta)*y + 1]
sage: S = R.quotient(i); S
Quotient of Multivariate Polynomial Ring in x, y, z over
Cyclotomic Field of order 3 and degree 2 by the ideal (x +
(-zeta)*y + 1, x^3 + (-zeta)*y^3)
sage: S.0 - zeta*S.1
-1
sage: S.0^3 - zeta*S.1^3
0
Two examples from the Mathematica documentation (done in Sage):
We compute a Groebner basis:
sage: R.<x,y> = PolynomialRing(QQ, order='lex') sage: ideal(x^2 - 2*y^2, x*y - 3).groebner_basis() [x - 2/3*y^3, y^4 - 9/2]We show that three polynomials have no common root:
sage: R.<x,y> = QQ[] sage: ideal(x+y, x^2 - 1, y^2 - 2*x).groebner_basis() [1]
The next example shows how we can use Groebner bases over  to
find the primes modulo which a system of equations has a solution,
when the system has no solutions over the rationals.
to
find the primes modulo which a system of equations has a solution,
when the system has no solutions over the rationals.
We first form a certain ideal
in
, and note that the Groebner basis of
over
contains 1, so there are no solutions over
or an algebraic closure of it (this is not surprising as there are 4 equations in 3 unknowns).
sage: P.<x,y,z> = PolynomialRing(ZZ,order='lex') sage: I = ideal(-y^2 - 3*y + z^2 + 3, -2*y*z + z^2 + 2*z + 1, \ x*z + y*z + z^2, -3*x*y + 2*y*z + 6*z^2) sage: I.change_ring(P.change_ring(QQ)).groebner_basis() [1]However, when we compute the Groebner basis of I (defined over
), we note that there is a certain integer in the ideal which is not 1.
sage: I.groebner_basis() [-x - y - z, -y^2 - 3*y + z^2 + 3, -y*z + 14329*y + 6653454247350, 2*y - 1199*z^3 + 74229*z^2 + 31017*z + 106019, -23*z^3 + 953554642851*z + 2034, 19*z^2 + 5357048579, 2*z - 1339262138, 164878]Now for each prime
dividing this integer 164878, the Groebner basis of I modulo
will be non-trivial and will thus give a solution of the original system modulo
.
sage: factor(164878) 2 * 7 * 11777 sage: I.change_ring(P.change_ring( GF(2) )).groebner_basis() [x + y + z, y^2 + y, y*z + y, z^2 + 1] sage: I.change_ring(P.change_ring( GF(7) )).groebner_basis() [x - 1, y + 3, z - 2] sage: I.change_ring(P.change_ring( GF(11777 ))).groebner_basis() [x + 5633, y - 3007, z - 2626]The Groebner basis modulo any product of the prime factors is also non-trivial.
sage: I.change_ring(P.change_ring( IntegerModRing(2*7) )).groebner_basis() [x*y + 10, x*z + 13*y + 9, 7*x + 7*y + 7*z, y^2 + 3*y, y*z + y + 2, 2*y + 6, z^2 + 3, 2*z + 10]Modulo any other prime the Groebner basis is trivial so there are no other solutions. For example:
sage: I.change_ring( P.change_ring( GF(3) ) ).groebner_basis() [1]
TESTS:
sage: x,y,z = QQ['x,y,z'].gens()
sage: I = ideal(x^5 + y^4 + z^3 - 1, x^3 + y^3 + z^2 - 1)
sage: I == loads(dumps(I))
True
Bases: sage.rings.polynomial.multi_polynomial_ideal.MPolynomialIdeal_singular_repr, sage.rings.polynomial.multi_polynomial_ideal.MPolynomialIdeal_macaulay2_repr, sage.rings.polynomial.multi_polynomial_ideal.MPolynomialIdeal_magma_repr, sage.rings.ideal.Ideal_generic
Return the ideal I in P spanned by
the generators 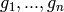 of self as returned by
self.gens().
of self as returned by
self.gens().
INPUT:
EXAMPLE:
sage: P.<x,y,z> = PolynomialRing(QQ,3,order='lex')
sage: I = sage.rings.ideal.Cyclic(P)
sage: I
Ideal (x + y + z, x*y + x*z + y*z, x*y*z - 1) of
Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.groebner_basis()
[x + y + z, y^2 + y*z + z^2, z^3 - 1]
sage: Q.<x,y,z> = P.change_ring(order='degrevlex'); Q
Multivariate Polynomial Ring in x, y, z over Rational Field
sage: Q.term_order()
Degree reverse lexicographic term order
sage: J = I.change_ring(Q); J
Ideal (x + y + z, x*y + x*z + y*z, x*y*z - 1) of
Multivariate Polynomial Ring in x, y, z over Rational Field
sage: J.groebner_basis()
[z^3 - 1, y^2 + y*z + z^2, x + y + z]
Return the reduced Groebner basis of this ideal. A Groebner
basis 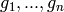 for an ideal
for an ideal  is a basis such that
is a basis such that
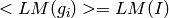 , i.e., the leading monomial ideal of
, i.e., the leading monomial ideal of
 is spanned by the leading terms of
is spanned by the leading terms of
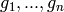 . Groebner bases are the key concept in
computational ideal theory in multivariate polynomial rings
which allows a variety of problems to be solved.
Additionally, a reduced Groebner basis
. Groebner bases are the key concept in
computational ideal theory in multivariate polynomial rings
which allows a variety of problems to be solved.
Additionally, a reduced Groebner basis  is a unique
representation for the ideal
is a unique
representation for the ideal 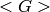 with respect to the chosen
monomial ordering.
with respect to the chosen
monomial ordering.
INPUT:
ALGORITHMS:
If only a system is given - e.g. ‘magma’ - the default algorithm is chosen for that system.
Note
The Singular and libSingular versions of the respective algorithms are identical, but the former calls an external Singular process while the later calls a C function, i.e. the calling overhead is smaller.
EXAMPLES:
Consider Katsura-3 over QQ with lexicographical term ordering. We compute the reduced Groebner basis using every available implementation and check their equality.
sage: P.<a,b,c> = PolynomialRing(QQ,3, order='lex')
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis()
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('libsingular:groebner')
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('libsingular:std')
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('libsingular:stdhilb')
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('libsingular:stdfglm')
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('libsingular:slimgb')
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
Note that toy:buchberger does not return the reduced Groebner basis,
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('toy:buchberger')
[a^2 - a + 2*b^2 + 2*c^2,
a*b + b*c - 1/2*b, a + 2*b + 2*c - 1,
b^2 + 3*b*c - 1/2*b + 3*c^2 - c,
b*c - 1/10*b + 6/5*c^2 - 2/5*c,
b + 30*c^3 - 79/7*c^2 + 3/7*c,
c^6 - 79/210*c^5 - 229/2100*c^4 + 121/2520*c^3 + 1/3150*c^2 - 11/12600*c,
c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
but that toy:buchberger2 does.
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('toy:buchberger2')
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('macaulay2:gb') # optional - macaulay2
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
sage: I = sage.rings.ideal.Katsura(P,3) # regenerate to prevent caching
sage: I.groebner_basis('magma:GroebnerBasis') # optional - magma
[a - 60*c^3 + 158/7*c^2 + 8/7*c - 1, b + 30*c^3 - 79/7*c^2 + 3/7*c, c^4 - 10/21*c^3 + 1/84*c^2 + 1/84*c]
Groebner bases over  can be computed.
can be computed.
sage: P.<a,b,c> = PolynomialRing(ZZ,3)
sage: I = P * (a + 2*b + 2*c - 1, a^2 - a + 2*b^2 + 2*c^2, 2*a*b + 2*b*c - b)
sage: I.groebner_basis()
[-b^3 + 23*b*c^2 - 3*b^2 - 5*b*c,
2*b*c^2 - 6*c^3 - b^2 - b*c + 2*c^2,
42*c^3 + 5*b^2 + 4*b*c - 14*c^2,
2*b^2 + 6*b*c + 6*c^2 - b - 2*c,
-10*b*c - 12*c^2 + b + 4*c,
a + 2*b + 2*c - 1]
sage: I.groebner_basis('macaulay2') # optional - macaulay2
[b^3 + b*c^2 + 12*c^3 + b^2 + b*c - 4*c^2,
2*b*c^2 - 6*c^3 + b^2 + 5*b*c + 8*c^2 - b - 2*c,
42*c^3 + b^2 + 2*b*c - 14*c^2 + b,
2*b^2 - 4*b*c - 6*c^2 + 2*c, 10*b*c + 12*c^2 - b - 4*c,
a + 2*b + 2*c - 1]
Groebner bases over 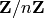 are also supported:
are also supported:
sage: P.<a,b,c> = PolynomialRing(Zmod(1000),3)
sage: I = P * (a + 2*b + 2*c - 1, a^2 - a + 2*b^2 + 2*c^2, 2*a*b + 2*b*c - b)
sage: I.groebner_basis()
[b*c^2 + 992*b*c + 712*c^2 + 332*b + 96*c,
2*c^3 + 589*b*c + 862*c^2 + 762*b + 268*c,
b^2 + 438*b*c + 281*b,
5*b*c + 156*c^2 + 112*b + 948*c,
50*c^2 + 600*b + 650*c, a + 2*b + 2*c + 999, 125*b]
Sage also supports local orderings:
sage: P.<x,y,z> = PolynomialRing(QQ,3,order='negdegrevlex')
sage: I = P * ( x*y*z + z^5, 2*x^2 + y^3 + z^7, 3*z^5 +y ^5 )
sage: I.groebner_basis()
[x^2 + 1/2*y^3, x*y*z + z^5, y^5 + 3*z^5, y^4*z - 2*x*z^5, z^6]
We can represent every element in the ideal as a combination of the generators using the lift() method:
sage: P.<x,y,z> = PolynomialRing(QQ,3)
sage: I = P * ( x*y*z + z^5, 2*x^2 + y^3 + z^7, 3*z^5 +y ^5 )
sage: J = Ideal(I.groebner_basis())
sage: f = sum(P.random_element(terms=2)*f for f in I.gens())
sage: f
1/2*y^2*z^7 - 1/4*y*z^8 + 2*x*z^5 + 95*z^6 + 1/2*y^5 - 1/4*y^4*z + x^2*y^2 + 3/2*x^2*y*z + 95*x*y*z^2
sage: f.lift(I.gens())
[2*x + 95*z, 1/2*y^2 - 1/4*y*z, 0]
sage: l = f.lift(J.gens()); l
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1/2*y^2 + 1/4*y*z, 1/2*y^2*z^2 - 1/4*y*z^3 + 2*x + 95*z]
sage: sum(map(mul, zip(l,J.gens()))) == f
True
Groebner bases over fraction fields of polynomial rings are also supported:
sage: P.<t> = QQ[]
sage: F = Frac(P)
sage: R.<X,Y,Z> = F[]
sage: I = Ideal([f + P.random_element() for f in sage.rings.ideal.Katsura(R).gens()])
sage: I.groebner_basis()
[Z^3 + (79/105*t^2 - 79/105*t + 79/630)*Z^2 + (-11/105*t^4 + 22/105*t^3 - 17/45*t^2 + 197/630*t + 557/1890)*Y + ...,
Y^2 + (-3/5)*Z^2 + (2/5*t^2 - 2/5*t + 1/15)*Y + (-2/5*t^2 + 2/5*t - 1/15)*Z - 1/10*t^4 + 1/5*t^3 - 7/30*t^2 + 2/5*t + 11/90,
Y*Z + 6/5*Z^2 + (1/5*t^2 - 1/5*t + 1/30)*Y + (4/5*t^2 - 4/5*t + 2/15)*Z + 1/5*t^4 - 2/5*t^3 + 7/15*t^2 - 3/10*t - 11/45, X + 2*Y + 2*Z + t^2 - t - 1/3]
ALGORITHM: Uses Singular, Magma (if available), Macaulay2 (if available), or a toy implementation.
Return the Groebner fan of this ideal.
The base ring must be  or a finite field
or a finite field
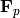 of with
of with 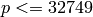 .
.
EXAMPLES:
sage: P.<x,y> = PolynomialRing(QQ)
sage: i = ideal(x^2 - y^2 + 1)
sage: g = i.groebner_fan()
sage: g.reduced_groebner_bases()
[[x^2 - y^2 + 1], [-x^2 + y^2 - 1]]
INPUT:
Return homogeneous ideal spanned by the homogeneous polynomials generated by homogenizing the generators of this ideal.
INPUT:
EXAMPLE:
sage: P.<x,y,z> = PolynomialRing(GF(2))
sage: I = Ideal([x^2*y + z + 1, x + y^2 + 1]); I
Ideal (x^2*y + z + 1, y^2 + x + 1) of Multivariate
Polynomial Ring in x, y, z over Finite Field of size 2
sage: I.homogenize()
Ideal (x^2*y + z*h^2 + h^3, y^2 + x*h + h^2) of
Multivariate Polynomial Ring in x, y, z, h over Finite
Field of size 2
sage: I.homogenize(y)
Ideal (x^2*y + y^3 + y^2*z, x*y) of Multivariate
Polynomial Ring in x, y, z over Finite Field of size 2
sage: I = Ideal([x^2*y + z^3 + y^2*x, x + y^2 + 1])
sage: I.homogenize()
Ideal (x^2*y + x*y^2 + z^3, y^2 + x*h + h^2) of
Multivariate Polynomial Ring in x, y, z, h over Finite
Field of size 2
Return True if this ideal is spanned by homogeneous polynomials, i.e. if it is a homogeneous ideal.
EXAMPLE:
sage: P.<x,y,z> = PolynomialRing(QQ,3)
sage: I = sage.rings.ideal.Katsura(P)
sage: I
Ideal (x + 2*y + 2*z - 1, x^2 + 2*y^2 + 2*z^2 - x, 2*x*y +
2*y*z - y) of Multivariate Polynomial Ring in x, y, z over
Rational Field
sage: I.is_homogeneous()
False
sage: J = I.homogenize()
sage: J
Ideal (x + 2*y + 2*z - h, x^2 + 2*y^2 + 2*z^2 - x*h, 2*x*y
+ 2*y*z - y*h) of Multivariate Polynomial Ring in x, y, z,
h over Rational Field
sage: J.is_homogeneous()
True
Returns a vector space basis (consisting of monomials) of the quotient ring by the ideal, resp. of a free module by the module, in case it is finite dimensional and if the input is a standard basis with respect to the ring ordering.
INPUT: algorithm - defaults to use libsingular, if it is anything else we will use the kbase() command
EXAMPLES:
sage: R.<x,y,z> = PolynomialRing(QQ)
sage: I = R.ideal(x^2+y^2+z^2-4, x^2+2*y^2-5, x*z-1)
sage: I.normal_basis()
[y*z^2, z^2, y*z, z, x*y, y, x, 1]
sage: I.normal_basis(algorithm='singular')
[y*z^2, z^2, y*z, z, x*y, y, x, 1]
Plot the real zero locus of this principal ideal.
INPUT:
self - a principal ideal in 2 variables
plot the ideal (default: None)
for plotting dimensions
implicit_plot
EXAMPLES:
Implicit plotting in 2-d:
sage: R.<x,y> = PolynomialRing(QQ,2)
sage: I = R.ideal([y^3 - x^2])
sage: I.plot() # cusp
sage: I = R.ideal([y^2 - x^2 - 1])
sage: I.plot((x,-3, 3), (y, -2, 2)) # hyperbola
sage: I = R.ideal([y^2 + x^2*(1/4) - 1])
sage: I.plot() # ellipse
sage: I = R.ideal([y^2-(x^2-1)*(x-2)])
sage: I.plot() # elliptic curve
sage: f = ((x+3)^3 + 2*(x+3)^2 - y^2)*(x^3 - y^2)*((x-3)^3-2*(x-3)^2-y^2)
sage: I = R.ideal(f)
sage: I.plot() # the Singular logo
This used to be trac #5267:
sage: I = R.ideal([-x^2*y+1])
sage: I.plot()
AUTHORS:
Reduce an element modulo the reduced Groebner basis for this ideal. This returns 0 if and only if the element is in this ideal. In any case, this reduction is unique up to monomial orders.
EXAMPLES:
sage: R.<x,y> = PolynomialRing(QQ, 2)
sage: I = (x^3 + y, y)*R
sage: I.reduce(y)
0
sage: I.reduce(x^3)
0
sage: I.reduce(x - y)
x
sage: I = (y^2 - (x^3 + x))*R
sage: I.reduce(x^3)
y^2 - x
sage: I.reduce(x^6)
y^4 - 2*x*y^2 + x^2
sage: (y^2 - x)^2
y^4 - 2*x*y^2 + x^2
Note
Requires computation of a Groebner basis, which can be a very expensive operation.
Compute the Weil restriction of this ideal over some extension field.
A Weil restriction of scalars - denoted 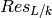 - is a
functor which, for any finite extension of fields
- is a
functor which, for any finite extension of fields 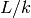 and
any algebraic variety
and
any algebraic variety  over
over  , produces another
corresponding variety
, produces another
corresponding variety 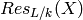 , defined over
, defined over  . It is
useful for reducing questions about varieties over large
fields to questions about more complicated varieties over
smaller fields.
. It is
useful for reducing questions about varieties over large
fields to questions about more complicated varieties over
smaller fields.
This function does not compute this Weil restriction directly but computes on generating sets of polynomial ideals:
Let  be the degree of the field extension
be the degree of the field extension 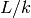 , let
, let  a
generator of
a
generator of 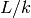 and
and  the minimal polynomial of
the minimal polynomial of
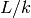 . Denote this ideal by
. Denote this ideal by  .
.
Specifically, this function first maps each variable  to
its representation over
to
its representation over  :
: 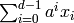 . Then
each generator of
. Then
each generator of  is evaluated over these representations
and reduced modulo the minimal polynomial
is evaluated over these representations
and reduced modulo the minimal polynomial  . The result is
interpreted as a univariate polynomial in
. The result is
interpreted as a univariate polynomial in  and its
coefficients are the new generators of the returned ideal.
and its
coefficients are the new generators of the returned ideal.
If the input and the output ideals are radical, this is equivalent to the statement about algebraic varieties above.
EXAMPLE:
sage: k.<a> = GF(2^2)
sage: P.<x,y> = PolynomialRing(k,2)
sage: I = Ideal([x*y + 1, a*x + 1])
sage: I.variety()
[{y: a, x: a + 1}]
sage: J = I.weil_restriction()
sage: J
Ideal (x1*y0 + x0*y1 + x1*y1, x0*y0 + x1*y1 + 1, x0 + x1, x1 + 1) of
Multivariate Polynomial Ring in x0, x1, y0, y1 over Finite Field of size 2
sage: J += sage.rings.ideal.FieldIdeal(J.ring()) # ensure radical ideal
sage: J.variety()
[{y1: 1, x1: 1, x0: 1, y0: 0}]
sage: J.weil_restriction() # returns J
Ideal (x1*y0 + x0*y1 + x1*y1, x0*y0 + x1*y1 + 1, x0 + x1, x1 + 1, x0^2 + x0,
x1^2 + x1, y0^2 + y0, y1^2 + y1)
of Multivariate Polynomial Ring in x0, x1, y0, y1 over Finite Field of size 2
sage: k.<a> = GF(3^5)
sage: P.<x,y,z> = PolynomialRing(k)
sage: I = sage.rings.ideal.Katsura(P)
sage: I.dimension()
0
sage: I.variety()
[{y: 0, z: 0, x: 1}]
sage: J = I.weil_restriction(); J
Ideal (x4 - y4 - z4, x3 - y3 - z3, x2 - y2 - z2, x1 - y1 - z1, x0 - y0 - z0 - 1,
x2^2 - x1*x3 - x0*x4 + x4^2 - y2^2 + y1*y3 + y0*y4 - y4^2 - z2^2 + z1*z3 + z0*z4 - z4^2 - x4,
-x1*x2 - x0*x3 - x3*x4 - x4^2 + y1*y2 + y0*y3 + y3*y4 + y4^2 + z1*z2 + z0*z3 + z3*z4 + z4^2 - x3,
x1^2 - x0*x2 + x3^2 - x2*x4 + x3*x4 - y1^2 + y0*y2 - y3^2 + y2*y4 - y3*y4 - z1^2 + z0*z2 - z3^2 + z2*z4 - z3*z4 - x2,
-x0*x1 - x2*x3 - x3^2 - x1*x4 + x2*x4 + y0*y1 + y2*y3 + y3^2 + y1*y4 - y2*y4 + z0*z1 + z2*z3 + z3^2 + z1*z4 - z2*z4 - x1,
x0^2 + x2*x3 + x1*x4 - y0^2 - y2*y3 - y1*y4 - z0^2 - z2*z3 - z1*z4 - x0,
-x4*y0 - x3*y1 - x2*y2 - x1*y3 - x0*y4 - x4*y4 - y4*z0 - y3*z1 - y2*z2 - y1*z3 - y0*z4 - y4*z4 - y4,
-x3*y0 - x2*y1 - x1*y2 - x0*y3 - x4*y3 - x3*y4 + x4*y4 - y3*z0 - y2*z1 - y1*z2 - y0*z3 - y4*z3 - y3*z4 + y4*z4 - y3,
-x2*y0 - x1*y1 - x0*y2 - x4*y2 - x3*y3 + x4*y3 - x2*y4 + x3*y4 - y2*z0 - y1*z1 - y0*z2 - y4*z2 - y3*z3 + y4*z3 - y2*z4 + y3*z4 - y2,
-x1*y0 - x0*y1 - x4*y1 - x3*y2 + x4*y2 - x2*y3 + x3*y3 - x1*y4 + x2*y4 - y1*z0 - y0*z1 - y4*z1 - y3*z2 + y4*z2 - y2*z3 + y3*z3 - y1*z4 + y2*z4 - y1,
-x0*y0 + x4*y1 + x3*y2 + x2*y3 + x1*y4 - y0*z0 + y4*z1 + y3*z2 + y2*z3 + y1*z4 - y0) of Multivariate Polynomial Ring in
x0, x1, x2, x3, x4, y0, y1, y2, y3, y4, z0, z1, z2, z3, z4 over Finite Field of size 3
sage: J += sage.rings.ideal.FieldIdeal(J.ring()) # ensure radical ideal
sage: J.variety()
[{y1: 0, y4: 0, x4: 0, y2: 0, y3: 0, y0: 0, x2: 0, z4: 0, z3: 0, z2: 0, x1: 0, z1: 0, z0: 0, x0: 1, x3: 0}]
Weil restrictions are often used to study elliptic curves over extension fields so we give a simple example involving those:
sage: K.<a> = QuadraticField(1/3)
sage: E = EllipticCurve(K,[1,2,3,4,5])
We pick a point on E:
sage: p = E.lift_x(1); p
(1 : 2 : 1)
sage: I = E.defining_ideal(); I
Ideal (-x^3 - 2*x^2*z + x*y*z + y^2*z - 4*x*z^2 + 3*y*z^2 - 5*z^3)
of Multivariate Polynomial Ring in x, y, z over Number Field in a with defining polynomial x^2 - 1/3
Of course, the point p is a root of all generators of I:
sage: [f.subs(x=1,y=2,z=1) for f in I.gens()]
[0]
I is also radical:
sage: I.radical() == I
True
So we compute its Weil restriction:
sage: J = I.weil_restriction()
sage: J
Ideal (-3*x0^2*x1 - 1/3*x1^3 - 4*x0*x1*z0 + x1*y0*z0 + x0*y1*z0 + 2*y0*y1*z0 - 4*x1*z0^2 + 3*y1*z0^2 - 2*x0^2*z1
- 2/3*x1^2*z1 + x0*y0*z1 + y0^2*z1 + 1/3*x1*y1*z1 + 1/3*y1^2*z1 - 8*x0*z0*z1 + 6*y0*z0*z1 - 15*z0^2*z1 - 4/3*x1*z1^2 + y1*z1^2 - 5/3*z1^3,
-x0^3 - x0*x1^2 - 2*x0^2*z0 - 2/3*x1^2*z0 + x0*y0*z0 + y0^2*z0 + 1/3*x1*y1*z0 + 1/3*y1^2*z0 - 4*x0*z0^2 + 3*y0*z0^2 - 5*z0^3 - 4/3*x0*x1*z1
+ 1/3*x1*y0*z1 + 1/3*x0*y1*z1 + 2/3*y0*y1*z1 - 8/3*x1*z0*z1 + 2*y1*z0*z1 - 4/3*x0*z1^2 + y0*z1^2 - 5*z0*z1^2)
of Multivariate Polynomial Ring in x0, x1, y0, y1, z0, z1 over Rational Field
We can check that the point p is still a root of all generators of J:
sage: [f.subs(x0=1,y0=2,z0=1,x1=0,y1=0,z1=0) for f in J.gens()]
[0, 0]
Note
Based on a Singular implementation by Michael Brickenstein
An ideal in a multivariate polynomial ring, which has an underlying Macaulay2 ring associated to it.
EXAMPLES:
sage: R.<x,y,z,w> = PolynomialRing(ZZ, 4)
sage: I = ideal(x*y-z^2, y^2-w^2)
sage: I
Ideal (x*y - z^2, y^2 - w^2) of Multivariate Polynomial Ring in x, y, z, w over Integer Ring
An ideal in a multivariate polynomial ring, which has an underlying Singular ring associated to it.
Return a list of the associated primes of primary ideals of
which the intersection is  = self.
= self.
An ideal 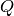 is called primary if it is a proper ideal of
the ring
is called primary if it is a proper ideal of
the ring  and if whenever
and if whenever 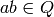 and
and
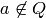 then
then 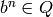 for some
for some
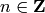 .
.
If 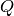 is a primary ideal of the ring
is a primary ideal of the ring  , then the
radical ideal
, then the
radical ideal  of
of 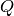 , i.e.
, i.e.
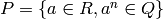 for some
for some
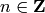 , is called the
associated prime of
, is called the
associated prime of 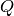 .
.
If  is a proper ideal of the ring
is a proper ideal of the ring  then there
exists a decomposition in primary ideals
then there
exists a decomposition in primary ideals 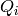 such that
such that

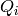 contains the intersection of the
rest, and
contains the intersection of the
rest, and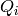 are pairwise
different.
are pairwise
different.This method returns the associated primes of the 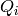 .
.
INPUT:
OUTPUT:
EXAMPLES:
sage: R.<x,y,z> = PolynomialRing(QQ, 3, order='lex')
sage: p = z^2 + 1; q = z^3 + 2
sage: I = (p*q^2, y-z^2)*R
sage: pd = I.associated_primes(); pd
[Ideal (z^3 + 2, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field,
Ideal (z^2 + 1, y + 1) of Multivariate Polynomial Ring in x, y, z over Rational Field]
ALGORITHM: Uses Singular.
REFERENCES:
Returns True if the generators of this ideal (self.gens()) form a Groebner basis.
Let  be the set of generators of this ideal. The check is
performed by trying to lift
be the set of generators of this ideal. The check is
performed by trying to lift 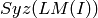 to
to 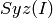 as
as  forms a Groebner basis if and only if for every element
forms a Groebner basis if and only if for every element  in
in
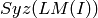 :
:
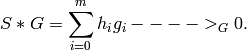
ALGORITHM: Uses Singular
EXAMPLE:
sage: R.<a,b,c,d,e,f,g,h,i,j> = PolynomialRing(GF(127),10)
sage: I = sage.rings.ideal.Cyclic(R,4)
sage: I.basis_is_groebner()
False
sage: I2 = Ideal(I.groebner_basis())
sage: I2.basis_is_groebner()
True
A more complicated example:
sage: R.<U6,U5,U4,U3,U2, u6,u5,u4,u3,u2, h> = PolynomialRing(GF(7583))
sage: l = [u6 + u5 + u4 + u3 + u2 - 3791*h, \
U6 + U5 + U4 + U3 + U2 - 3791*h, \
U2*u2 - h^2, U3*u3 - h^2, U4*u4 - h^2, \
U5*u4 + U5*u3 + U4*u3 + U5*u2 + U4*u2 + U3*u2 - 3791*U5*h - 3791*U4*h - 3791*U3*h - 3791*U2*h - 2842*h^2, \
U4*u5 + U3*u5 + U2*u5 + U3*u4 + U2*u4 + U2*u3 - 3791*u5*h - 3791*u4*h - 3791*u3*h - 3791*u2*h - 2842*h^2, \
U5*u5 - h^2, U4*U2*u3 + U5*U3*u2 + U4*U3*u2 + U3^2*u2 - 3791*U5*U3*h - 3791*U4*U3*h - 3791*U3^2*h - 3791*U5*U2*h \
- 3791*U4*U2*h + U3*U2*h - 3791*U2^2*h - 3791*U4*u3*h - 3791*U4*u2*h - 3791*U3*u2*h - 2843*U5*h^2 + 1897*U4*h^2 - 946*U3*h^2 - 947*U2*h^2 + 2370*h^3, \
U3*u5*u4 + U2*u5*u4 + U3*u4^2 + U2*u4^2 + U2*u4*u3 - 3791*u5*u4*h - 3791*u4^2*h - 3791*u4*u3*h - 3791*u4*u2*h + u5*h^2 - 2842*u4*h^2, \
U2*u5*u4*u3 + U2*u4^2*u3 + U2*u4*u3^2 - 3791*u5*u4*u3*h - 3791*u4^2*u3*h - 3791*u4*u3^2*h - 3791*u4*u3*u2*h + u5*u4*h^2 + u4^2*h^2 + u5*u3*h^2 - 2842*u4*u3*h^2, \
U5^2*U4*u3 + U5*U4^2*u3 + U5^2*U4*u2 + U5*U4^2*u2 + U5^2*U3*u2 + 2*U5*U4*U3*u2 + U5*U3^2*u2 - 3791*U5^2*U4*h - 3791*U5*U4^2*h - 3791*U5^2*U3*h \
+ U5*U4*U3*h - 3791*U5*U3^2*h - 3791*U5^2*U2*h + U5*U4*U2*h + U5*U3*U2*h - 3791*U5*U2^2*h - 3791*U5*U3*u2*h - 2842*U5^2*h^2 + 1897*U5*U4*h^2 \
- U4^2*h^2 - 947*U5*U3*h^2 - U4*U3*h^2 - 948*U5*U2*h^2 - U4*U2*h^2 - 1422*U5*h^3 + 3791*U4*h^3, \
u5*u4*u3*u2*h + u4^2*u3*u2*h + u4*u3^2*u2*h + u4*u3*u2^2*h + 2*u5*u4*u3*h^2 + 2*u4^2*u3*h^2 + 2*u4*u3^2*h^2 + 2*u5*u4*u2*h^2 + 2*u4^2*u2*h^2 \
+ 2*u5*u3*u2*h^2 + 1899*u4*u3*u2*h^2, \
U5^2*U4*U3*u2 + U5*U4^2*U3*u2 + U5*U4*U3^2*u2 - 3791*U5^2*U4*U3*h - 3791*U5*U4^2*U3*h - 3791*U5*U4*U3^2*h - 3791*U5*U4*U3*U2*h \
+ 3791*U5*U4*U3*u2*h + U5^2*U4*h^2 + U5*U4^2*h^2 + U5^2*U3*h^2 - U4^2*U3*h^2 - U5*U3^2*h^2 - U4*U3^2*h^2 - U5*U4*U2*h^2 \
- U5*U3*U2*h^2 - U4*U3*U2*h^2 + 3791*U5*U4*h^3 + 3791*U5*U3*h^3 + 3791*U4*U3*h^3, \
u4^2*u3*u2*h^2 + 1515*u5*u3^2*u2*h^2 + u4*u3^2*u2*h^2 + 1515*u5*u4*u2^2*h^2 + 1515*u5*u3*u2^2*h^2 + u4*u3*u2^2*h^2 \
+ 1521*u5*u4*u3*h^3 - 3028*u4^2*u3*h^3 - 3028*u4*u3^2*h^3 + 1521*u5*u4*u2*h^3 - 3028*u4^2*u2*h^3 + 1521*u5*u3*u2*h^3 + 3420*u4*u3*u2*h^3, \
U5^2*U4*U3*U2*h + U5*U4^2*U3*U2*h + U5*U4*U3^2*U2*h + U5*U4*U3*U2^2*h + 2*U5^2*U4*U3*h^2 + 2*U5*U4^2*U3*h^2 + 2*U5*U4*U3^2*h^2 \
+ 2*U5^2*U4*U2*h^2 + 2*U5*U4^2*U2*h^2 + 2*U5^2*U3*U2*h^2 - 2*U4^2*U3*U2*h^2 - 2*U5*U3^2*U2*h^2 - 2*U4*U3^2*U2*h^2 \
- 2*U5*U4*U2^2*h^2 - 2*U5*U3*U2^2*h^2 - 2*U4*U3*U2^2*h^2 - U5*U4*U3*h^3 - U5*U4*U2*h^3 - U5*U3*U2*h^3 - U4*U3*U2*h^3]
sage: Ideal(l).basis_is_groebner()
False
sage: gb = Ideal(l).groebner_basis()
sage: Ideal(gb).basis_is_groebner()
True
Note
From the Singular Manual for the reduce function we use in this method: ‘The result may have no meaning if the second argument (self) is not a standard basis’. I (malb) believe this refers to the mathematical fact that the results may have no meaning if self is no standard basis, i.e., Singular doesn’t ‘add’ any additional ‘nonsense’ to the result. So we may actually use reduce to determine if self is a Groebner basis.
Return a list of primary ideals and their associated primes such
that the intersection of the primary ideal 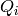 is
is
 = self.
= self.
An ideal 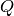 is called primary if it is a proper ideal of
the ring
is called primary if it is a proper ideal of
the ring  and if whenever
and if whenever 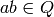 and
and
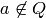 then
then 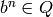 for some
for some
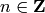 .
.
If 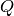 is a primary ideal of the ring
is a primary ideal of the ring  , then the
radical ideal
, then the
radical ideal  of
of 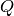 , i.e.
, i.e.
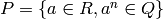 for some
for some
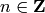 , is called the
associated prime of
, is called the
associated prime of 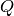 .
.
If  is a proper ideal of the ring
is a proper ideal of the ring  then there
exists a decomposition in primary ideals
then there
exists a decomposition in primary ideals 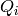 such that
such that

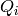 contains the intersection of the
rest, and
contains the intersection of the
rest, and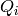 are pairwise
different.
are pairwise
different.This method returns these 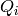 and their associated
primes.
and their associated
primes.
INPUT:
OUTPUT:
EXAMPLES:
sage: R.<x,y,z> = PolynomialRing(QQ, 3, order='lex')
sage: p = z^2 + 1; q = z^3 + 2
sage: I = (p*q^2, y-z^2)*R
sage: pd = I.complete_primary_decomposition(); pd
[(Ideal (z^6 + 4*z^3 + 4, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field,
Ideal (z^3 + 2, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field),
(Ideal (z^2 + 1, y + 1) of Multivariate Polynomial Ring in x, y, z over Rational Field,
Ideal (z^2 + 1, y + 1) of Multivariate Polynomial Ring in x, y, z over Rational Field)]
sage: I.complete_primary_decomposition(algorithm = 'gtz')
[(Ideal (z^6 + 4*z^3 + 4, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field,
Ideal (z^3 + 2, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field),
(Ideal (z^2 + 1, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field,
Ideal (z^2 + 1, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field)]
sage: reduce(lambda Qi,Qj: Qi.intersection(Qj), [Qi for (Qi,radQi) in pd]) == I
True
sage: [Qi.radical() == radQi for (Qi,radQi) in pd]
[True, True]
sage: P.<x,y,z> = PolynomialRing(ZZ)
sage: I = ideal( x^2 - 3*y, y^3 - x*y, z^3 - x, x^4 - y*z + 1 )
sage: I.complete_primary_decomposition()
...
ValueError: Coefficient ring must be a field for function 'complete_primary_decomposition'.
ALGORITHM: Uses Singular.
Note
See [BW93] for an introduction to primary decomposition.
The dimension of the ring modulo this ideal.
EXAMPLE:
sage: P.<x,y,z> = PolynomialRing(GF(32003),order='degrevlex')
sage: I = ideal(x^2-y,x^3)
sage: I.dimension()
1
For polynomials over a finite field of order too large for Singular, this falls back on a toy implementation of Buchberger to compute the Groebner basis, then uses the algorithm described in Chapter 9, Section 1 of Cox, Little, and O’Shea’s “Ideals, Varieties, and Algorithms”.
EXAMPLE:
sage: R.<x,y> = PolynomialRing(GF(2147483659),order='lex')
sage: I = R.ideal([x*y,x*y+1])
sage: I.dimension()
verbose 0 (...: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation.
0
sage: I=ideal([x*(x*y+1),y*(x*y+1)])
sage: I.dimension()
verbose 0 (...: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation.
1
sage: I = R.ideal([x^3*y,x*y^2])
sage: I.dimension()
verbose 0 (...: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation.
1
sage: R.<x,y> = PolynomialRing(GF(2147483659),order='lex')
sage: I = R.ideal(0)
sage: I.dimension()
verbose 0 (...: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation.
2
ALGORITHM: Uses Singular, unless the characteristic is too large.
Note
Requires computation of a Groebner basis, which can be a very expensive operation.
Returns the elimination ideal this ideal with respect to the variables given in variables.
INPUT:
EXAMPLE:
sage: R.<x,y,t,s,z> = PolynomialRing(QQ,5)
sage: I = R * [x-t,y-t^2,z-t^3,s-x+y^3]
sage: I.elimination_ideal([t,s])
Ideal (y^2 - x*z, x*y - z, x^2 - y) of Multivariate
Polynomial Ring in x, y, t, s, z over Rational Field
ALGORITHM: Uses SINGULAR
Note
Requires computation of a Groebner basis, which can be a very expensive operation.
Return the genus of the projective curve defined by this ideal, which must be 1 dimensional.
EXAMPLE:
Consider the hyperelliptic curve 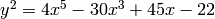 over
over  , it has genus 2:
, it has genus 2:
sage: P, x = PolynomialRing(QQ,"x").objgen()
sage: f = 4*x^5 - 30*x^3 + 45*x - 22
sage: C = HyperellipticCurve(f); C
Hyperelliptic Curve over Rational Field defined by y^2 = 4*x^5 - 30*x^3 + 45*x - 22
sage: C.genus()
2
sage: P.<x,y> = PolynomialRing(QQ)
sage: f = y^2 - 4*x^5 - 30*x^3 + 45*x - 22
sage: I = Ideal([f])
sage: I.genus()
2
Return the Hilbert polynomial of this ideal.
Let  = self be a homogeneous ideal and
= self be a homogeneous ideal and
 = self.ring() be a graded commutative
algebra (
= self.ring() be a graded commutative
algebra (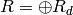 ) over a field
) over a field  . The
Hilbert polynomial is the unique polynomial
. The
Hilbert polynomial is the unique polynomial 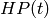 with
rational coefficients such that
with
rational coefficients such that 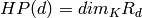 for
all but finitely many positive integers
for
all but finitely many positive integers  .
.
EXAMPLE:
sage: P.<x,y,z> = PolynomialRing(QQ)
sage: I = Ideal([x^3*y^2 + 3*x^2*y^2*z + y^3*z^2 + z^5])
sage: I.hilbert_polynomial()
5*t - 5
Return the Hilbert series of this ideal.
Let  = self be a homogeneous ideal and
= self be a homogeneous ideal and
 = self.ring() be a graded commutative
algebra (
= self.ring() be a graded commutative
algebra (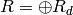 ) over a field
) over a field
 . Then the Hilbert function is defined as
. Then the Hilbert function is defined as
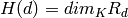 and the Hilbert series of
and the Hilbert series of  is defined as the formal power series
is defined as the formal power series
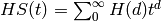 .
.
This power series can be expressed as
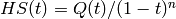 where
where 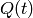 is a polynomial
over
is a polynomial
over 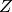 and
and  the number of variables in
the number of variables in
 . This method returns
. This method returns 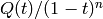 .
.
EXAMPLE:
sage: P.<x,y,z> = PolynomialRing(QQ)
sage: I = Ideal([x^3*y^2 + 3*x^2*y^2*z + y^3*z^2 + z^5])
sage: I.hilbert_series()
(-t^4 - t^3 - t^2 - t - 1)/(-t^2 + 2*t - 1)
Let  = self.
= self.
Returns the integral closure of 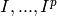 , where
, where 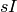 is
an ideal in the polynomial ring
is
an ideal in the polynomial ring ![R=k[x(1),...x(n)]](../../../_images/math/e40906712a2fcdd278efa78dbb8791c8b9ce34b3.png) . If
. If  is
not given, or
is
not given, or 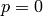 , compute the closure of all powers up to
the maximum degree in t occurring in the closure of
, compute the closure of all powers up to
the maximum degree in t occurring in the closure of ![R[It]](../../../_images/math/f97eb67195583e6c1a9b77cec60e48b3b7fcf18f.png) (so this is the last power whose closure is not just the
sum/product of the smaller). If
(so this is the last power whose closure is not just the
sum/product of the smaller). If  is given and r is
True, I.integral_closure() starts with a check whether I
is already a radical ideal.
is given and r is
True, I.integral_closure() starts with a check whether I
is already a radical ideal.
INPUT:
EXAMPLE:
sage: R.<x,y> = QQ[]
sage: I = ideal([x^2,x*y^4,y^5])
sage: I.integral_closure()
[x^2, y^5, -x*y^3]
ALGORITHM: Use Singular
If this ideal is spanned by 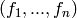 this method
returns
this method
returns 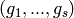 such that:
such that:
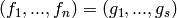
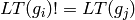 for all
for all 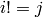
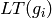 does not divide
does not divide  for all monomials
for all monomials  of
of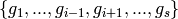
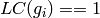 for all
for all  if the coefficient ring is a field.
if the coefficient ring is a field.
EXAMPLE:
sage: R.<x,y,z> = PolynomialRing(QQ)
sage: I = Ideal([z*x+y^3,z+y^3,z+x*y])
sage: I.interreduced_basis()
[y^3 + z, x*y + z, x*z - z]
Note that tail reduction for local orderings is not well-defined:
sage: R.<x,y,z> = PolynomialRing(QQ,order='negdegrevlex')
sage: I = Ideal([z*x+y^3,z+y^3,z+x*y])
sage: I.interreduced_basis()
[z + x*y, x*y - y^3, x^2*y - y^3]
A fixed error with nonstandard base fields:
sage: R.<t>=QQ['t']
sage: K.<x,y>=R.fraction_field()['x,y']
sage: I=t*x*K
sage: I.interreduced_basis()
[x]
ALGORITHM: Uses Singular’s interred command or sage.rings.polynomial.toy_buchberger.inter_reduction`() if conversion to Singular fails.
Return the intersection of the two ideals.
EXAMPLES:
sage: R.<x,y> = PolynomialRing(QQ, 2, order='lex')
sage: I = x*R
sage: J = y*R
sage: I.intersection(J)
Ideal (x*y) of Multivariate Polynomial Ring in x, y over Rational Field
The following simple example illustrates that the product need not equal the intersection.
sage: I = (x^2, y)*R
sage: J = (y^2, x)*R
sage: K = I.intersection(J); K
Ideal (y^2, x*y, x^2) of Multivariate Polynomial Ring in x, y over Rational Field
sage: IJ = I*J; IJ
Ideal (x^2*y^2, x^3, y^3, x*y) of Multivariate Polynomial Ring in x, y over Rational Field
sage: IJ == K
False
OUTPUT:
EXAMPLES:
sage: R.<x,y,z> = PolynomialRing(QQ, 3, 'xyz')
sage: p = z^2 + 1; q = z^3 + 2
sage: I = (p*q^2, y-z^2)*R
sage: I.minimal_associated_primes ()
[Ideal (z^2 + 1, -z^2 + y) of Multivariate Polynomial Ring
in x, y, z over Rational Field, Ideal (z^3 + 2, -z^2 + y)
of Multivariate Polynomial Ring in x, y, z over Rational
Field]
ALGORITHM: Uses Singular.
If you somehow manage to install surf, perhaps you can use this function to implicitly plot the real zero locus of this ideal (if principal).
INPUT:
EXAMPLES:
Implicit plotting in 2-d:
sage: R.<x,y> = PolynomialRing(QQ,2)
sage: I = R.ideal([y^3 - x^2])
sage: I.plot() # cusp
sage: I = R.ideal([y^2 - x^2 - 1])
sage: I.plot() # hyperbola
sage: I = R.ideal([y^2 + x^2*(1/4) - 1])
sage: I.plot() # ellipse
sage: I = R.ideal([y^2-(x^2-1)*(x-2)])
sage: I.plot() # elliptic curve
Implicit plotting in 3-d:
sage: R.<x,y,z> = PolynomialRing(QQ,3)
sage: I = R.ideal([y^2 + x^2*(1/4) - z])
sage: I.plot() # a cone optional - surf
sage: I = R.ideal([y^2 + z^2*(1/4) - x])
sage: I.plot() # same code, from a different angle optional - surf
sage: I = R.ideal([x^2*y^2+x^2*z^2+y^2*z^2-16*x*y*z])
sage: I.plot() # Steiner surface optional - surf
AUTHORS:
Return a list of primary ideals such that their intersection is
 = self.
= self.
An ideal 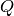 is called primary if it is a proper ideal of
the ring
is called primary if it is a proper ideal of
the ring  and if whenever
and if whenever 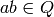 and
and
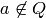 then
then 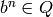 for some
for some
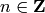 .
.
If  is a proper ideal of the ring
is a proper ideal of the ring  then there
exists a decomposition in primary ideals
then there
exists a decomposition in primary ideals 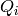 such that
such that

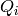 contains the intersection of the
rest, and
contains the intersection of the
rest, and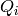 are pairwise
different.
are pairwise
different.This method returns these 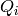 .
.
INPUT:
- 'gtz' - use the gianni-trager-zacharias algorithm
EXAMPLES:
sage: R.<x,y,z> = PolynomialRing(QQ, 3, order='lex')
sage: p = z^2 + 1; q = z^3 + 2
sage: I = (p*q^2, y-z^2)*R
sage: pd = I.primary_decomposition(); pd
[Ideal (z^6 + 4*z^3 + 4, y - z^2) of Multivariate Polynomial Ring in x, y, z over Rational Field,
Ideal (z^2 + 1, y + 1) of Multivariate Polynomial Ring in x, y, z over Rational Field]
sage: reduce(lambda Qi,Qj: Qi.intersection(Qj), pd) == I
True
ALGORITHM: Uses Singular.
REFERENCES:
Given ideals  = self and
= self and 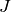 in the same polynomial
ring
in the same polynomial
ring  , return the ideal quotient of
, return the ideal quotient of  by
by 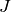 consisting
of the polynomials
consisting
of the polynomials  of
of  such that
such that 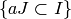 .
.
This is also referred to as the colon ideal
( :
: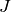 ).
).
INPUT:
EXAMPLE:
sage: R.<x,y,z> = PolynomialRing(GF(181),3)
sage: I = Ideal([x^2+x*y*z,y^2-z^3*y,z^3+y^5*x*z])
sage: J = Ideal([x])
sage: Q = I.quotient(J)
sage: y*z + x in I
False
sage: x in J
True
sage: x * (y*z + x) in I
True
The radical of this ideal.
EXAMPLES:
This is an obviously not radical ideal:
sage: R.<x,y,z> = PolynomialRing(QQ, 3)
sage: I = (x^2, y^3, (x*z)^4 + y^3 + 10*x^2)*R
sage: I.radical()
Ideal (y, x) of Multivariate Polynomial Ring in x, y, z over Rational Field
That the radical is correct is clear from the Groebner basis.
sage: I.groebner_basis()
[y^3, x^2]
This is the example from the Singular manual:
sage: p = z^2 + 1; q = z^3 + 2
sage: I = (p*q^2, y-z^2)*R
sage: I.radical()
Ideal (z^2 - y, y^2*z + y*z + 2*y + 2) of Multivariate Polynomial Ring in x, y, z over Rational Field
Note
From the Singular manual: A combination of the algorithms of Krick/Logar and Kemper is used. Works also in positive characteristic (Kempers algorithm).
sage: R.<x,y,z> = PolynomialRing(GF(37), 3)
sage: p = z^2 + 1; q = z^3 + 2
sage: I = (p*q^2, y - z^2)*R
sage: I.radical()
Ideal (z^2 - y, y^2*z + y*z + 2*y + 2) of Multivariate Polynomial Ring in x, y, z over Finite Field of size 37
Warning
This function is deprecated. It will be removed in a future release of Sage. Please use the interreduced_basis() function instead.
If this ideal is spanned by 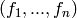 this method
returns
this method
returns 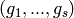 such that:
such that:
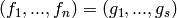
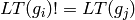 for all
for all 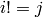
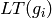 does not divide
does not divide  for all monomials
for all monomials  of
of 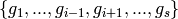
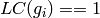 for all
for all  .
.EXAMPLES:
sage: R.<x,y,z> = PolynomialRing(QQ)
sage: I = Ideal([z*x+y^3,z+y^3,z+x*y])
sage: I.reduced_basis()
doctest:...: DeprecationWarning: This function is deprecated. It will be removed in a future release of Sage. Please use the interreduced_basis() function instead.
[y^3 + z, x*y + z, x*z - z]
sage: R.<x,y,z> = PolynomialRing(QQ,order='negdegrevlex')
sage: I = Ideal([z*x+y^3,z+y^3,z+x*y])
sage: I.reduced_basis()
[z + x*y, x*y - y^3, x^2*y - y^3]
ALGORITHM:
Uses Singular’s interred command or toy_buchberger.inter_reduction if conversion to Singular fails.
Computes the first syzygy (i.e., the module of relations of the given generators) of the ideal.
EXAMPLE:
sage: R.<x,y> = PolynomialRing(QQ)
sage: f = 2*x^2 + y
sage: g = y
sage: h = 2*f + g
sage: I = Ideal([f,g,h])
sage: M = I.syzygy_module(); M
[ -2 -1 1]
[ -y 2*x^2 + y 0]
sage: G = vector(I.gens())
sage: M*G
(0, 0)
ALGORITHM: Uses Singular’s syz command
Returns a lex or other_ring Groebner Basis for this ideal.
INPUT:
algorithm - see below for options.
provided conversion will be performed to this ring. Otherwise a lex Groebner basis will be returned.
ALGORITHMS:
EXAMPLES:
sage: R.<x,y,z> = PolynomialRing(QQ,3)
sage: I = Ideal([y^3+x^2,x^2*y+x^2, x^3-x^2, z^4-x^2-y])
sage: I = Ideal(I.groebner_basis())
sage: S.<z,x,y> = PolynomialRing(QQ,3,order='lex')
sage: J = Ideal(I.transformed_basis('fglm',S))
sage: J
Ideal (z^4 + y^3 - y, x^2 + y^3, x*y^3 - y^3, y^4 + y^3)
of Multivariate Polynomial Ring in z, x, y over Rational Field
sage: R.<z,y,x>=PolynomialRing(GF(32003),3,order='lex')
sage: I=Ideal([y^3+x*y*z+y^2*z+x*z^3,3+x*y+x^2*y+y^2*z])
sage: I.transformed_basis('gwalk')
[z*y^2 + y*x^2 + y*x + 3,
z*x + 8297*y^8*x^2 + 8297*y^8*x + 3556*y^7 - 8297*y^6*x^4 + 15409*y^6*x^3 - 8297*y^6*x^2
- 8297*y^5*x^5 + 15409*y^5*x^4 - 8297*y^5*x^3 + 3556*y^5*x^2 + 3556*y^5*x + 3556*y^4*x^3
+ 3556*y^4*x^2 - 10668*y^4 - 10668*y^3*x - 8297*y^2*x^9 - 1185*y^2*x^8 + 14224*y^2*x^7
- 1185*y^2*x^6 - 8297*y^2*x^5 - 14223*y*x^7 - 10666*y*x^6 - 10666*y*x^5 - 14223*y*x^4
+ x^5 + 2*x^4 + x^3,
y^9 - y^7*x^2 - y^7*x - y^6*x^3 - y^6*x^2 - 3*y^6 - 3*y^5*x - y^3*x^7 - 3*y^3*x^6
- 3*y^3*x^5 - y^3*x^4 - 9*y^2*x^5 - 18*y^2*x^4 - 9*y^2*x^3 - 27*y*x^3 - 27*y*x^2 - 27*x]
ALGORITHM: Uses Singular
Decompose zero-dimensional ideal self into triangular sets.
This requires that the given basis is reduced w.r.t. to the lexicographical monomial ordering. If the basis of self does not have this property, the required Groebner basis is computed implicitly.
INPUT:
ALGORITHMS:
OUTPUT: a list 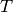 of lists
of lists  such that the variety of
self is the union of the varieties of
such that the variety of
self is the union of the varieties of  in
in  and each
and each
 is in triangular form.
is in triangular form.
EXAMPLE:
sage: P.<e,d,c,b,a> = PolynomialRing(QQ,5,order='lex')
sage: I = sage.rings.ideal.Cyclic(P)
sage: GB = Ideal(I.groebner_basis('libsingular:stdfglm'))
sage: GB.triangular_decomposition('singular:triangLfak')
[Ideal (a - 1, b - 1, c - 1, d^2 + 3*d + 1, e + d + 3) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a - 1, b - 1, c^2 + 3*c + 1, d + c + 3, e - 1) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a - 1, b^2 + 3*b + 1, c + b + 3, d - 1, e - 1) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a - 1, b^4 + b^3 + b^2 + b + 1, c - b^2, d - b^3, e + b^3 + b^2 + b + 1) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^2 + 3*a + 1, b - 1, c - 1, d - 1, e + a + 3) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^2 + 3*a + 1, b + a + 3, c - 1, d - 1, e - 1) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^4 - 4*a^3 + 6*a^2 + a + 1, 11*b^2 - 6*b*a^3 + 26*b*a^2 - 41*b*a + 4*b + 8*a^3 - 31*a^2 + 40*a + 24, 11*c + 3*a^3 - 13*a^2 + 26*a - 2, 11*d + 3*a^3 - 13*a^2 + 26*a - 2, 11*e + 11*b - 6*a^3 + 26*a^2 - 41*a + 4) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^4 + a^3 + a^2 + a + 1, b - 1, c + a^3 + a^2 + a + 1, d - a^3, e - a^2) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^4 + a^3 + a^2 + a + 1, b - a, c - a, d^2 + 3*d*a + a^2, e + d + 3*a) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^4 + a^3 + a^2 + a + 1, b - a, c^2 + 3*c*a + a^2, d + c + 3*a, e - a) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^4 + a^3 + a^2 + a + 1, b^2 + 3*b*a + a^2, c + b + 3*a, d - a, e - a) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^4 + a^3 + a^2 + a + 1, b^3 + b^2*a + b^2 + b*a^2 + b*a + b + a^3 + a^2 + a + 1, c + b^2*a^3 + b^2*a^2 + b^2*a + b^2, d - b^2*a^2 - b^2*a - b^2 - b*a^2 - b*a - a^2, e - b^2*a^3 + b*a^2 + b*a + b + a^2 + a) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field,
Ideal (a^4 + a^3 + 6*a^2 - 4*a + 1, 11*b^2 - 6*b*a^3 - 10*b*a^2 - 39*b*a - 2*b - 16*a^3 - 23*a^2 - 104*a + 24, 11*c + 3*a^3 + 5*a^2 + 25*a + 1, 11*d + 3*a^3 + 5*a^2 + 25*a + 1, 11*e + 11*b - 6*a^3 - 10*a^2 - 39*a - 2) of Multivariate Polynomial Ring in e, d, c, b, a over Rational Field]
sage: R.<x1,x2> = PolynomialRing(QQ, 2, order='lex')
sage: f1 = 1/2*((x1^2 + 2*x1 - 4)*x2^2 + 2*(x1^2 + x1)*x2 + x1^2)
sage: f2 = 1/2*((x1^2 + 2*x1 + 1)*x2^2 + 2*(x1^2 + x1)*x2 - 4*x1^2)
sage: I = Ideal(f1,f2)
sage: I.triangular_decomposition()
[Ideal (x2, x1^2) of Multivariate Polynomial Ring in x1, x2 over Rational Field,
Ideal (x2, x1^2) of Multivariate Polynomial Ring in x1, x2 over Rational Field,
Ideal (x2, x1^2) of Multivariate Polynomial Ring in x1, x2 over Rational Field,
Ideal (x2^4 + 4*x2^3 - 6*x2^2 - 20*x2 + 5, 8*x1 - x2^3 + x2^2 + 13*x2 - 5) of Multivariate Polynomial Ring in x1, x2 over Rational Field]
Return the variety of self.
Given a zero-dimensional ideal  (== self) of a
polynomial ring P whose order is lexicographic, return the
variety of I as a list of dictionaries with (variable, value)
pairs. By default, the variety of the ideal over its
coefficient field
(== self) of a
polynomial ring P whose order is lexicographic, return the
variety of I as a list of dictionaries with (variable, value)
pairs. By default, the variety of the ideal over its
coefficient field  is returned; ring can be specified
to find the variety over a different ring.
is returned; ring can be specified
to find the variety over a different ring.
These dictionaries have cardinality equal to the number of variables in P and represent assignments of values to these variables such that all polynomials in I vanish.
If ring is specified, then a triangular decomposition of
self is found over the original coefficient field  ;
then the triangular systems are solved using root-finding over
ring. This is particularly useful when
;
then the triangular systems are solved using root-finding over
ring. This is particularly useful when  is QQ (to
allow fast symbolic computation of the triangular
decomposition) and ring is RR, AA, CC, or
QQbar (to compute the whole real or complex variety of the
ideal).
is QQ (to
allow fast symbolic computation of the triangular
decomposition) and ring is RR, AA, CC, or
QQbar (to compute the whole real or complex variety of the
ideal).
Note that with ring``=``RR or CC, computation is done numerically and potentially inaccurately; in particular, the number of points in the real variety may be miscomputed. With ring``=``AA or QQbar, computation is done exactly (which may be much slower, of course).
INPUT:
EXAMPLE:
sage: K.<w> = GF(27) # this example is from the MAGMA handbook
sage: P.<x, y> = PolynomialRing(K, 2, order='lex')
sage: I = Ideal([ x^8 + y + 2, y^6 + x*y^5 + x^2 ])
sage: I = Ideal(I.groebner_basis()); I
Ideal (x - y^47 - y^45 + y^44 - y^43 + y^41 - y^39 - y^38
- y^37 - y^36 + y^35 - y^34 - y^33 + y^32 - y^31 + y^30 +
y^28 + y^27 + y^26 + y^25 - y^23 + y^22 + y^21 - y^19 -
y^18 - y^16 + y^15 + y^13 + y^12 - y^10 + y^9 + y^8 + y^7
- y^6 + y^4 + y^3 + y^2 + y - 1, y^48 + y^41 - y^40 + y^37
- y^36 - y^33 + y^32 - y^29 + y^28 - y^25 + y^24 + y^2 + y
+ 1) of Multivariate Polynomial Ring in x, y over Finite
Field in w of size 3^3
sage: V = I.variety(); V
[{y: w^2 + 2, x: 2*w}, {y: w^2 + w, x: 2*w + 1}, {y: w^2 + 2*w, x: 2*w + 2}]
sage: [f.subs(v) for f in I.gens() for v in V] # check that all polynomials vanish
[0, 0, 0, 0, 0, 0]
However, we only account for solutions in the ground field and not in the algebraic closure:
sage: I.vector_space_dimension()
48
Here we compute the points of intersection of a hyperbola and a circle, in several fields:
sage: K.<x, y> = PolynomialRing(QQ, 2, order='lex')
sage: I = Ideal([ x*y - 1, (x-2)^2 + (y-1)^2 - 1])
sage: I = Ideal(I.groebner_basis()); I
Ideal (x + y^3 - 2*y^2 + 4*y - 4, y^4 - 2*y^3 + 4*y^2 - 4*y + 1)
of Multivariate Polynomial Ring in x, y over Rational Field
These two curves have one rational intersection:
sage: I.variety()
[{y: 1, x: 1}]
There are two real intersections:
sage: I.variety(ring=RR)
[{y: 0.361103080528647, x: 2.76929235423863},
{y: 1.00000000000000, x: 1.00000000000000}]
sage: I.variety(ring=AA)
[{x: 2.769292354238632?, y: 0.3611030805286474?},
{x: 1, y: 1}]
and a total of four intersections:
sage: I.variety(ring=CC)
[{y: 0.31944845973567... - 1.6331702409152...*I,
x: 0.11535382288068... + 0.58974280502220...*I},
{y: 0.31944845973567... + 1.6331702409152...*I,
x: 0.11535382288068... - 0.58974280502220...*I},
{y: 0.36110308052864..., x: 2.7692923542386...},
{y: 1.00000000000000, x: 1.00000000000000}]
sage: I.variety(ring=QQbar)
[{y: 0.3194484597356763? - 1.633170240915238?*I,
x: 0.11535382288068429? + 0.5897428050222055?*I},
{y: 0.3194484597356763? + 1.633170240915238?*I,
x: 0.11535382288068429? - 0.5897428050222055?*I},
{y: 0.3611030805286474?, x: 2.769292354238632?},
{y: 1, x: 1}]
Computation over floating point numbers may compute only a partial solution, or even none at all. Notice that x values are missing from the following variety:
sage: R.<x,y> = CC[]
sage: I = ideal([x^2+y^2-1,x*y-1])
sage: I.variety()
verbose 0 (...: multi_polynomial_ideal.py, variety) Warning: computations in the complex field are inexact; variety may be computed partially or incorrectly.
verbose 0 (...: multi_polynomial_ideal.py, variety) Warning: falling back to very slow toy implementation.
[{y: -0.86602540378443... - 0.500000000000000*I},
{y: -0.86602540378443... + 0.500000000000000*I},
{y: 0.86602540378443... - 0.500000000000000*I},
{y: 0.86602540378443... + 0.500000000000000*I}]
This is due to precision error, which causes the computation of an intermediate Groebner basis to fail.
If the ground field’s characteristic is too large for Singular, we resort to a toy implementation:
sage: R.<x,y> = PolynomialRing(GF(2147483659),order='lex')
sage: I=ideal([x^3-2*y^2,3*x+y^4])
sage: I.variety()
verbose 0 (...: multi_polynomial_ideal.py, groebner_basis) Warning: falling back to very slow toy implementation.
verbose 0 (...: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation.
verbose 0 (...: multi_polynomial_ideal.py, variety) Warning: falling back to very slow toy implementation.
[{y: 0, x: 0}]
TESTS:
sage: K.<w> = GF(27)
sage: P.<x, y> = PolynomialRing(K, 2, order='lex')
sage: I = Ideal([ x^8 + y + 2, y^6 + x*y^5 + x^2 ])
Testing the robustness of the Singular interface
sage: T = I.triangular_decomposition('singular:triangLfak')
sage: I.variety()
[{y: w^2 + 2, x: 2*w}, {y: w^2 + w, x: 2*w + 1}, {y: w^2 + 2*w, x: 2*w + 2}]
Testing that a bug is indeed fixed.
sage: R = PolynomialRing(GF(2), 30, ['x%d'%(i+1) for i in range(30)], order='lex')
sage: R.inject_variables()
Defining...
sage: I = Ideal([x1 + 1, x2, x3 + 1, x5*x10 + x10 + x18, x5*x11 + x11, \
x5*x18, x6, x7 + 1, x9, x10*x11 + x10 + x18, x10*x18 + x18, \
x11*x18, x12, x13, x14, x15, x16 + 1, x17 + x18 + 1, x19, x20, \
x21 + 1, x22, x23, x24, x25 + 1, x28 + 1, x29 + 1, x30, x8, \
x26, x1^2 + x1, x2^2 + x2, x3^2 + x3, x4^2 + x4, x5^2 + x5, \
x6^2 + x6, x7^2 + x7, x8^2 + x8, x9^2 + x9, x10^2 + x10, \
x11^2 + x11, x12^2 + x12, x13^2 + x13, x14^2 + x14, x15^2 + x15, \
x16^2 + x16, x17^2 + x17, x18^2 + x18, x19^2 + x19, x20^2 + x20, \
x21^2 + x21, x22^2 + x22, x23^2 + x23, x24^2 + x24, x25^2 + x25, \
x26^2 + x26, x27^2 + x27, x28^2 + x28, x29^2 + x29, x30^2 + x30])
sage: I.basis_is_groebner()
True
sage: for V in I.variety():
... print V
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 0, x19: 0, x18: 1, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 0, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 1, x19: 0, x18: 1, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 0, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 0, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 0, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 0, x19: 0, x18: 0, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 1, x4: 1, x19: 0, x18: 0, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 1, x25: 1, x9: 0, x8: 0, x20: 0, x17: 1, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 0, x19: 0, x18: 1, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 0, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
{x14: 0, x24: 0, x16: 1, x1: 1, x3: 1, x2: 0, x5: 0, x4: 1, x19: 0, x18: 1, x7: 1, x6: 0, x10: 1, x30: 0, x28: 1, x29: 1, x13: 0, x27: 1, x11: 0, x25: 1, x9: 0, x8: 0, x20: 0, x17: 0, x23: 0, x26: 0, x15: 0, x21: 1, x12: 0, x22: 0}
Check that the issue at trac 7425 is fixed:
sage: R.<x, y, z> = QQ[]
sage: I = R.ideal([x^2-y^3*z, x+y*z])
sage: I.dimension()
1
sage: I.variety()
...
ValueError: The dimension of the ideal is 1, but it should be 0
ALGORITHM: Uses triangular decomposition.
Return the vector space dimension of the ring modulo this ideal. If the ideal is not zero-dimensional, a TypeError is raised.
ALGORITHM: Uses Singular.
EXAMPLE:
sage: R.<u,v> = PolynomialRing(QQ)
sage: g = u^4 + v^4 + u^3 + v^3
sage: I = ideal(g) + ideal(g.gradient())
sage: I.dimension()
0
sage: I.vector_space_dimension()
4
Within this context all Singular Groebner basis calculations are reduced automatically.
AUTHORS:
Bases: sage.misc.method_decorator.MethodDecorator
Decorator which throws an exception if a computation over a coefficient ring which is not a field is attempted.
Note
This decorator is used automatically internally so the user does not need to use it manually.
Return True if the provided argument x is an ideal in the multivariate polynomial ring.
INPUT:
EXAMPLES:
sage: from sage.rings.polynomial.all import is_MPolynomialIdeal
sage: P.<x,y,z> = PolynomialRing(QQ)
sage: I = [x + 2*y + 2*z - 1, x^2 + 2*y^2 + 2*z^2 - x, 2*x*y + 2*y*z - y]
Sage distinguishes between a list of generators for an ideal and the ideal itself. This distinction is inconsistent with Singular but matches Magma’s behavior.
sage: is_MPolynomialIdeal(I)
False
sage: I = Ideal(I)
sage: is_MPolynomialIdeal(I)
True
Decorator to force a reduced Singular groebner basis.
TESTS:
sage: P.<a,b,c,d,e> = PolynomialRing(GF(127))
sage: J = sage.rings.ideal.Cyclic(P).homogenize()
sage: from sage.misc.sageinspect import sage_getsource
sage: "buchberger" in sage_getsource(J.interreduced_basis)
True
Note
This decorator is used automatically internally so the user does not need to use it manually.