Multivariate Polynomial Rings over Generic Rings

Sage implements multivariate polynomial rings through several backends. This generic implementation uses the classes PolyDict and ETuple to construct a dictionary with exponent tuples as keys and coefficients as values.

AUTHORS:

• David Joyner and William Stein
• Kiran S. Kedlaya (2006-02-12): added Macaulay2 analogues of Singular features
• Martin Albrecht (2006-04-21): reorganize class hierarchy for singular rep
• Martin Albrecht (2007-04-20): reorganized class hierarchy to support Pyrex implementations
• Robert Bradshaw (2007-08-15): Coercions from rings in a subset of the variables.

EXAMPLES:

We construct the Frobenius morphism on over :

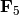sage: R, (x,y,z) = PolynomialRing(GF(5), 3, 'xyz').objgens()
sage: frob = R.hom([x^5, y^5, z^5])
sage: frob(x^2 + 2*y - z^4)
-z^20 + x^10 + 2*y^5
sage: frob((x + 2*y)^3)
x^15 + x^10*y^5 + 2*x^5*y^10 - 2*y^15
sage: (x^5 + 2*y^5)^3
x^15 + x^10*y^5 + 2*x^5*y^10 - 2*y^15

We make a polynomial ring in one variable over a polynomial ring in two variables:

sage: R.<x, y> = PolynomialRing(QQ, 2)
sage: S.<t> = PowerSeriesRing(R)
sage: t*(x+y)
(x + y)*t

class sage.rings.polynomial.multi_polynomial_ring.MPolynomialRing_macaulay2_repr

is_exact()

class sage.rings.polynomial.multi_polynomial_ring.MPolynomialRing_polydict(base_ring, n, names, order)

Bases: sage.rings.polynomial.multi_polynomial_ring.MPolynomialRing_macaulay2_repr, sage.rings.polynomial.polynomial_singular_interface.PolynomialRing_singular_repr, sage.rings.polynomial.multi_polynomial_ring_generic.MPolynomialRing_generic

Multivariable polynomial ring.

EXAMPLES:

sage: R = PolynomialRing(Integers(12), 'x', 5); R
Multivariate Polynomial Ring in x0, x1, x2, x3, x4 over Ring of integers modulo 12
sage: loads(R.dumps()) == R    
True

class sage.rings.polynomial.multi_polynomial_ring.MPolynomialRing_polydict_domain(base_ring, n, names, order)

Bases: sage.rings.ring.IntegralDomain, sage.rings.polynomial.multi_polynomial_ring.MPolynomialRing_polydict, sage.rings.polynomial.multi_polynomial_ring.MPolynomialRing_macaulay2_repr

ideal(*gens, **kwds)

Create an ideal in this polynomial ring.

is_field(proof=True)

is_integral_domain(proof=True)

monomial_all_divisors(t)

Return a list of all monomials that divide t, coefficients are ignored.

INPUT:

• t - a monomial

OUTPUT: a list of monomials

EXAMPLE:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.monomial_all_divisors(x^2*z^3)
[x, x^2, z, x*z, x^2*z, z^2, x*z^2, x^2*z^2, z^3, x*z^3, x^2*z^3]

ALGORITHM: addwithcarry idea by Toon Segers

monomial_divides(a, b)

Return False if a does not divide b and True otherwise.

INPUT:

• a - monomial
• b - monomial

EXAMPLES:

sage: P.<x,y,z>=MPolynomialRing(ZZ,3, order='degrevlex')
doctest:1: DeprecationWarning: MPolynomialRing is deprecated, use PolynomialRing instead!
sage: P.monomial_divides(x*y*z, x^3*y^2*z^4)
True
sage: P.monomial_divides(x^3*y^2*z^4, x*y*z)
False

TESTS:

sage: P.<x,y,z>=MPolynomialRing(ZZ,3, order='degrevlex')
sage: P.monomial_divides(P(1), P(0))
True
sage: P.monomial_divides(P(1), x)
True

monomial_lcm(f, g)

LCM for monomials. Coefficients are ignored.

INPUT:

• f - monomial
• g - monomial

EXAMPLE:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.monomial_lcm(3/2*x*y,x)
x*y

TESTS:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: R.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.monomial_lcm(x*y,R.gen())
x*y

sage: P.monomial_lcm(P(3/2),P(2/3))
1

sage: P.monomial_lcm(x,P(1))
x

monomial_pairwise_prime(h, g)

Return True if h and g are pairwise prime. Both are treated as monomials.

INPUT:

• h - monomial
• g - monomial

EXAMPLES:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.monomial_pairwise_prime(x^2*z^3, y^4)
True

sage: P.monomial_pairwise_prime(1/2*x^3*y^2, 3/4*y^3)
False

TESTS:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: Q.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.monomial_pairwise_prime(x^2*z^3, Q('y^4'))
True

sage: P.monomial_pairwise_prime(1/2*x^3*y^2, Q(0))
True

sage: P.monomial_pairwise_prime(P(1/2),x)
False

monomial_quotient(f, g, coeff=False)

Return f/g, where both f and g are treated as monomials. Coefficients are ignored by default.

INPUT:

• f - monomial
• g - monomial
• coeff - divide coefficients as well (default: False)

EXAMPLE:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ, 3, order='degrevlex')
sage: P.monomial_quotient(3/2*x*y,x)
y

sage: P.monomial_quotient(3/2*x*y,2*x,coeff=True)
3/4*y

TESTS:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: R.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: P.monomial_quotient(x*y,x)
y

sage: P.monomial_quotient(x*y,R.gen())
y

sage: P.monomial_quotient(P(0),P(1))
0

sage: P.monomial_quotient(P(1),P(0))
...
ZeroDivisionError

sage: P.monomial_quotient(P(3/2),P(2/3), coeff=True)
9/4

sage: P.monomial_quotient(x,y) # Note the wrong result
x*y^-1

sage: P.monomial_quotient(x,P(1))
x

Note

Assumes that the head term of f is a multiple of the head term of g and return the multiplicant m. If this rule is violated, funny things may happen.

monomial_reduce(f, G)

Try to find a g in G where g.lm() divides f. If found (g,flt) is returned, (0,0) otherwise, where flt is f/g.lm().

It is assumed that G is iterable and contains ONLY elements in self.

INPUT:

• f - monomial
• G - list/set of mpolynomials

EXAMPLES:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: f = x*y^2
sage: G = [ 3/2*x^3 + y^2 + 1/2, 1/4*x*y + 2/7, P(1/2)  ]
sage: P.monomial_reduce(f,G)
(y, 1/4*x*y + 2/7)

TESTS:

sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict_domain
sage: P.<x,y,z>=MPolynomialRing_polydict_domain(QQ,3, order='degrevlex')
sage: f = x*y^2
sage: G = [ 3/2*x^3 + y^2 + 1/2, 1/4*x*y + 2/7, P(1/2)  ]

sage: P.monomial_reduce(P(0),G)
(0, 0)

sage: P.monomial_reduce(f,[P(0)])
(0, 0)