AUTHORS:
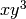 ; added examples of the new
R.x,y = PolynomialRing(QQ,2) notation.
; added examples of the new
R.x,y = PolynomialRing(QQ,2) notation.EXAMPLES:
We verify Lagrange’s four squares identity:
sage: R.<a0,a1,a2,a3,b0,b1,b2,b3> = QQbar[]
sage: (a0^2 + a1^2 + a2^2 + a3^2)*(b0^2 + b1^2 + b2^2 + b3^2) == (a0*b0 - a1*b1 - a2*b2 - a3*b3)^2 + (a0*b1 + a1*b0 + a2*b3 - a3*b2)^2 + (a0*b2 - a1*b3 + a2*b0 + a3*b1)^2 + (a0*b3 + a1*b2 - a2*b1 + a3*b0)^2
True
Bases: sage.rings.polynomial.multi_polynomial.MPolynomial
Bases: sage.rings.polynomial.polynomial_singular_interface.Polynomial_singular_repr, sage.rings.polynomial.multi_polynomial_element.MPolynomial_element
Multivariate polynomials implemented in pure python using polydicts.
Return the coefficient of the variables with the degrees specified in the python dictionary degrees. Mathematically, this is the coefficient in the base ring adjoined by the variables of this ring not listed in degrees. However, the result has the same parent as this polynomial.
This function contrasts with the function monomial_coefficient which returns the coefficient in the base ring of a monomial.
INPUT:
OUTPUT: element of the parent of self
See also
For coefficients of specific monomials, look at monomial_coefficient().
EXAMPLES:
sage: R.<x, y> = QQbar[]
sage: f = 2 * x * y
sage: c = f.coefficient({x:1,y:1}); c
2
sage: c.parent()
Multivariate Polynomial Ring in x, y over Algebraic Field
sage: c in PolynomialRing(QQbar, 2, names = ['x','y'])
True
sage: f = y^2 - x^9 - 7*x + 5*x*y
sage: f.coefficient({y:1})
5*x
sage: f.coefficient({y:0})
-x^9 + (-7)*x
sage: f.coefficient({x:0,y:0})
0
sage: f=(1+y+y^2)*(1+x+x^2)
sage: f.coefficient({x:0})
y^2 + y + 1
sage: f.coefficient([0,None])
y^2 + y + 1
sage: f.coefficient(x)
y^2 + y + 1
sage: # Be aware that this may not be what you think!
sage: # The physical appearance of the variable x is deceiving -- particularly if the exponent would be a variable.
sage: f.coefficient(x^0) # outputs the full polynomial
x^2*y^2 + x^2*y + x*y^2 + x^2 + x*y + y^2 + x + y + 1
sage: R.<x,y> = RR[]
sage: f=x*y+5
sage: c=f.coefficient({x:0,y:0}); c
5.00000000000000
sage: parent(c)
Multivariate Polynomial Ring in x, y over Real Field with 53 bits of precision
AUTHORS:
Return the constant coefficient of this multivariate polynomial.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.constant_coefficient()
5
sage: f = 3*x^2
sage: f.constant_coefficient()
0
Return the degree of self in x, where x must be one of the generators for the parent of self.
INPUT:
OUTPUT: integer
EXAMPLE:
sage: R.<x,y> = RR[]
sage: f = y^2 - x^9 - x
sage: f.degree(x)
9
sage: f.degree(y)
2
sage: (y^10*x - 7*x^2*y^5 + 5*x^3).degree(x)
3
sage: (y^10*x - 7*x^2*y^5 + 5*x^3).degree(y)
10
Returns a tuple (precisely - an ETuple) with the degree of each variable in this polynomial. The list of degrees is, of course, ordered by the order of the generators.
EXAMPLES:
sage: R.<x,y,z>=PolynomialRing(QQbar)
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.degrees()
(2, 2, 0)
sage: f = x^2+z^2
sage: f.degrees()
(2, 0, 2)
sage: f.total_degree() # this simply illustrates that total degree is not the sum of the degrees
2
sage: R.<x,y,z,u>=PolynomialRing(QQbar)
sage: f=(1-x)*(1+y+z+x^3)^5
sage: f.degrees()
(16, 5, 5, 0)
sage: R(0).degrees()
(0, 0, 0, 0)
Return the exponents of the monomials appearing in self.
EXAMPLES:
sage: R.<a,b,c> = PolynomialRing(QQbar, 3)
sage: f = a^3 + b + 2*b^2
sage: f.exponents()
[(3, 0, 0), (0, 2, 0), (0, 1, 0)]
Compute the irreducible factorization of this polynomial.
INPUT:
ALGORITHM: Use univariate factorization code.
If a polynomial is univariate, the appropriate univariate factorization code is called.
sage: R.<z> = PolynomialRing(CC,1)
sage: f = z^4 - 6*z + 3
sage: f.factor()
(z - 1.60443920904349) * (z - 0.511399619393097) * (z + 1.05791941421830 - 1.59281852704435*I) * (z + 1.05791941421830 + 1.59281852704435*I)
TESTS:
Check if we can handle polynomials with no variables, #7950:
sage: P = PolynomialRing(ZZ,0,'')
sage: res = P(10).factor(); res
2 * 5
sage: res[0][0].parent()
Multivariate Polynomial Ring in no variables over Integer Ring
sage: R = PolynomialRing(QQ,0,'')
sage: res = R(10).factor(); res
10
sage: res.unit().parent()
Rational Field
sage: P(0).factor()
...
ArithmeticError: Prime factorization of 0 not defined.
Check if we can factor constant polynomial, #8207:
sage: R.<x,y> = CC[]
sage: R(1).factor()
1.00000000000000
True if polynomial is constant, and False otherwise.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.is_constant()
False
sage: g = 10*x^0
sage: g.is_constant()
True
Returns True if self is a generator of it’s parent.
EXAMPLES:
sage: R.<x,y>=QQbar[]
sage: x.is_generator()
True
sage: (x+y-y).is_generator()
True
sage: (x*y).is_generator()
False
Return True if self is a homogeneous polynomial.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: (x+y).is_homogeneous()
True
sage: (x.parent()(0)).is_homogeneous()
True
sage: (x+y^2).is_homogeneous()
False
sage: (x^2 + y^2).is_homogeneous()
True
sage: (x^2 + y^2*x).is_homogeneous()
False
sage: (x^2*y + y^2*x).is_homogeneous()
True
Returns True if self is a monomial. A monomial is defined to be a product of generators with coefficient 1.
EXAMPLES:
sage: R.<x,y>=QQbar[]
sage: x.is_monomial()
True
sage: (x+2*y).is_monomial()
False
sage: (2*x).is_monomial()
False
sage: (x*y).is_monomial()
True
Return True if self is a unit.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: (x+y).is_unit()
False
sage: R(0).is_unit()
False
sage: R(-1).is_unit()
True
sage: R(-1 + x).is_unit()
False
sage: R(2).is_unit()
True
Returns True if this multivariate polynomial is univariate and False otherwise.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.is_univariate()
False
sage: g = f.subs({x:10}); g
700*y^2 + (-2)*y + 305
sage: g.is_univariate()
True
sage: f = x^0
sage: f.is_univariate()
True
Returns the leading coefficient of self i.e., self.coefficient(self.lm())
EXAMPLES:
sage: R.<x,y,z>=QQbar[]
sage: f=3*x^2-y^2-x*y
sage: f.lc()
3
given an ideal I = (f_1,...,f_r) and some g (== self) in I, find s_1,...,s_r such that g = s_1 f_1 + ... + s_r f_r
ALGORITHM: Use Singular.
EXAMPLE:
sage: A.<x,y> = PolynomialRing(CC,2,order='degrevlex')
sage: I = A.ideal([x^10 + x^9*y^2, y^8 - x^2*y^7 ])
sage: f = x*y^13 + y^12
sage: M = f.lift(I)
sage: M
[y^7, x^7*y^2 + x^8 + x^5*y^3 + x^6*y + x^3*y^4 + x^4*y^2 + x*y^5 + x^2*y^3 + y^4]
sage: sum( map( mul , zip( M, I.gens() ) ) ) == f
True
Returns the lead monomial of self with respect to the term order of self.parent().
EXAMPLES:
sage: R.<x,y,z>=PolynomialRing(GF(7),3,order='lex')
sage: (x^1*y^2 + y^3*z^4).lm()
x*y^2
sage: (x^3*y^2*z^4 + x^3*y^2*z^1).lm()
x^3*y^2*z^4
sage: R.<x,y,z>=PolynomialRing(CC,3,order='deglex')
sage: (x^1*y^2*z^3 + x^3*y^2*z^0).lm()
x*y^2*z^3
sage: (x^1*y^2*z^4 + x^1*y^1*z^5).lm()
x*y^2*z^4
sage: R.<x,y,z>=PolynomialRing(QQbar,3,order='degrevlex')
sage: (x^1*y^5*z^2 + x^4*y^1*z^3).lm()
x*y^5*z^2
sage: (x^4*y^7*z^1 + x^4*y^2*z^3).lm()
x^4*y^7*z
TESTS:
sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict
sage: R.<x,y>=MPolynomialRing_polydict(GF(2),2,order='lex')
sage: f=x+y
sage: f.lm()
x
Returns the leading term of self i.e., self.lc()*self.lm(). The notion of “leading term” depends on the ordering defined in the parent ring.
EXAMPLES:
sage: R.<x,y,z>=PolynomialRing(QQbar)
sage: f=3*x^2-y^2-x*y
sage: f.lt()
3*x^2
sage: R.<x,y,z>=PolynomialRing(QQbar,order="invlex")
sage: f=3*x^2-y^2-x*y
sage: f.lt()
-y^2
TESTS:
sage: from sage.rings.polynomial.multi_polynomial_ring import MPolynomialRing_polydict
sage: R.<x,y>=MPolynomialRing_polydict(GF(2),2,order='lex')
sage: f=x+y
sage: f.lt()
x
Return the coefficient in the base ring of the monomial mon in self, where mon must have the same parent as self.
This function contrasts with the function coefficient which returns the coefficient of a monomial viewing this polynomial in a polynomial ring over a base ring having fewer variables.
INPUT:
OUTPUT: coefficient in base ring
See also
For coefficients in a base ring of fewer variables, look at coefficient().
EXAMPLES:
The parent of the return is a member of the base ring.
sage: R.<x,y>=QQbar[]
The parent of the return is a member of the base ring.
sage: f = 2 * x * y
sage: c = f.monomial_coefficient(x*y); c
2
sage: c.parent()
Algebraic Field
sage: f = y^2 + y^2*x - x^9 - 7*x + 5*x*y
sage: f.monomial_coefficient(y^2)
1
sage: f.monomial_coefficient(x*y)
5
sage: f.monomial_coefficient(x^9)
-1
sage: f.monomial_coefficient(x^10)
0
sage: var('a')
a
sage: K.<a> = NumberField(a^2+a+1)
sage: P.<x,y> = K[]
sage: f=(a*x-1)*((a+1)*y-1); f
-x*y + (-a)*x + (-a - 1)*y + 1
sage: f.monomial_coefficient(x)
-a
Returns the list of monomials in self. The returned list is decreasingly ordered by the term ordering of self.parent().
OUTPUT: list of MPolynomials representing Monomials
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.monomials()
[x^2*y^2, x^2, y, 1]
sage: R.<fx,fy,gx,gy> = QQbar[]
sage: F = ((fx*gy - fy*gx)^3)
sage: F
-fy^3*gx^3 + 3*fx*fy^2*gx^2*gy + (-3)*fx^2*fy*gx*gy^2 + fx^3*gy^3
sage: F.monomials()
[fy^3*gx^3, fx*fy^2*gx^2*gy, fx^2*fy*gx*gy^2, fx^3*gy^3]
sage: F.coefficients()
[-1, 3, -3, 1]
sage: sum(map(mul,zip(F.coefficients(),F.monomials()))) == F
True
Number of variables in this polynomial
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.nvariables ()
2
sage: g = f.subs({x:10}); g
700*y^2 + (-2)*y + 305
sage: g.nvariables ()
1
A decorator to be used on binary operation methods that should operate on elements of the same parent. If the parents of the arguments differ, coercion is performed, then the method is re-looked up by name on the first argument.
In short, using the NamedBinopMethod (alias coerce_binop) decorator on a method gives it the exact same semantics of the basic arithmetic operations like _add_, _sub_, etc. in that both operands are guaranteed to have exactly the same parent.
Reduce this polynomial by the the polynomials in I.
INPUT:
EXAMPLE:
sage: P.<x,y,z> = QQbar[]
sage: f1 = -2 * x^2 + x^3
sage: f2 = -2 * y + x* y
sage: f3 = -x^2 + y^2
sage: F = Ideal([f1,f2,f3])
sage: g = x*y - 3*x*y^2
sage: g.reduce(F)
(-6)*y^2 + 2*y
sage: g.reduce(F.gens())
(-6)*y^2 + 2*y
sage: f = 3*x
sage: f.reduce([2*x,y])
0
sage: k.<w> = CyclotomicField(3)
sage: A.<y9,y12,y13,y15> = PolynomialRing(k)
sage: J = [ y9 + y12]
sage: f = y9 - y12; f.reduce(J)
-2*y12
sage: f = y13*y15; f.reduce(J)
y13*y15
sage: f = y13*y15 + y9 - y12; f.reduce(J)
y13*y15 - 2*y12
Fixes some given variables in a given multivariate polynomial and returns the changed multivariate polynomials. The polynomial itself is not affected. The variable,value pairs for fixing are to be provided as a dictionary of the form {variable:value}.
This is a special case of evaluating the polynomial with some of the variables constants and the others the original variables.
INPUT:
OUTPUT: new MPolynomial
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = x^2 + y + x^2*y^2 + 5
sage: f((5,y))
25*y^2 + y + 30
sage: f.subs({x:5})
25*y^2 + y + 30
Return the total degree of self, which is the maximum degree of any monomial in self.
EXAMPLES:
sage: R.<x,y,z> = QQbar[]
sage: f=2*x*y^3*z^2
sage: f.total_degree()
6
sage: f=4*x^2*y^2*z^3
sage: f.total_degree()
7
sage: f=99*x^6*y^3*z^9
sage: f.total_degree()
18
sage: f=x*y^3*z^6+3*x^2
sage: f.total_degree()
10
sage: f=z^3+8*x^4*y^5*z
sage: f.total_degree()
10
sage: f=z^9+10*x^4+y^8*x^2
sage: f.total_degree()
10
Returns a univariate polynomial associated to this multivariate polynomial.
INPUT:
If this polynomial is not in at most one variable, then a ValueError exception is raised. This is checked using the is_univariate() method. The new Polynomial is over the same base ring as the given MPolynomial.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.univariate_polynomial()
...
TypeError: polynomial must involve at most one variable
sage: g = f.subs({x:10}); g
700*y^2 + (-2)*y + 305
sage: g.univariate_polynomial ()
700*y^2 - 2*y + 305
sage: g.univariate_polynomial(PolynomialRing(QQ,'z'))
700*z^2 - 2*z + 305
TESTS:
sage: P = PolynomialRing(QQ, 0, '')
sage: P(5).univariate_polynomial()
5
Returns  -th variable occurring in this polynomial.
-th variable occurring in this polynomial.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.variable(0)
x
sage: f.variable(1)
y
Returns the tuple of variables occurring in this polynomial.
EXAMPLES:
sage: R.<x,y> = QQbar[]
sage: f = 3*x^2 - 2*y + 7*x^2*y^2 + 5
sage: f.variables()
(x, y)
sage: g = f.subs({x:10}); g
700*y^2 + (-2)*y + 305
sage: g.variables()
(y,)
TESTS:
This shows that the issue at trac ticket 7077 is fixed:
sage: x,y,z=polygens(QQ,'x,y,z')
sage: (x^2).variables()
(x,)
INPUT:
OUTPUT:
Note
This function is dependent on the ordering of a python dict. Thus, it isn’t really mathematically well-defined. I think that it should made a method of the FractionFieldElement class and rewritten.
EXAMPLES:
sage: R1 = PolynomialRing(FiniteField(5), 3, names = ["a","b","c"])
sage: F = FractionField(R1)
sage: a,b,c = R1.gens()
sage: f = 3*a*b^2*c^3+4*a*b*c
sage: g = a^2*b*c^2+2*a^2*b^4*c^7
Consider the quotient
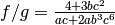 (note the
cancellation).
(note the
cancellation).
sage: r = f/g; r
(-2*b*c^2 - 1)/(2*a*b^3*c^6 + a*c)
sage: degree_lowest_rational_function(r,a)
(-1, 3)
sage: degree_lowest_rational_function(r,b)
(0, 4)
sage: degree_lowest_rational_function(r,c)
(-1, 4)