Ideals¶

Sage provides functionality for computing with ideals. One can create an ideal in any commutative ring $R$ by giving a list of generators, using the notation R.ideal([a,b,...]).

sage.rings.ideal.Cyclic(R, n=None, homog=False, singular=Singular)¶

Ideal of cyclic n-roots from 1-st n variables of R if R is coercible to Singular. If n==None n is set to R.ngens()

INPUT:

R - base ring to construct ideal for
n - number of cyclic roots (default: None)
homog - if True a homogeneous ideal is returned using the last variable in the ideal (default: False)
singular - singular instance to use

Note

R will be set as the active ring in Singular

EXAMPLES:

An example from a multivariate polynomial ring over the rationals:

sage: P.<x,y,z> = PolynomialRing(QQ,3,order='lex')
sage: I = sage.rings.ideal.Cyclic(P)
sage: I
Ideal (x + y + z, x*y + x*z + y*z, x*y*z - 1) of Multivariate Polynomial
Ring in x, y, z over Rational Field
sage: I.groebner_basis()
[x + y + z, y^2 + y*z + z^2, z^3 - 1]

We compute a Groebner basis for cyclic 6, which is a standard benchmark and test ideal:

sage: R.<x,y,z,t,u,v> = QQ['x,y,z,t,u,v']
sage: I = sage.rings.ideal.Cyclic(R,6)
sage: B = I.groebner_basis()
sage: len(B)
45

sage.rings.ideal.FieldIdeal(R)¶

Let q = R.base_ring().order() and (x0,...,x_n) = R.gens() then if q is finite this constructor returns

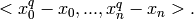
$< x_0^q - x_0, ... , x_n^q - x_n >.$

We call this ideal the field ideal and the generators the field equations.

EXAMPLES:

The Field Ideal generated from the polynomial ring over two variables in the finite field of size 2:

sage: P.<x,y> = PolynomialRing(GF(2),2)
sage: I = sage.rings.ideal.FieldIdeal(P); I
Ideal (x^2 + x, y^2 + y) of Multivariate Polynomial Ring in x, y over
Finite Field of size 2

Another, similar example:

sage: Q.<x1,x2,x3,x4> = PolynomialRing(GF(2^4,name='alpha'), 4)
sage: J = sage.rings.ideal.FieldIdeal(Q); J
Ideal (x1^16 + x1, x2^16 + x2, x3^16 + x3, x4^16 + x4) of
Multivariate Polynomial Ring in x1, x2, x3, x4 over Finite
Field in alpha of size 2^4

sage.rings.ideal.Ideal(*args, **kwds)¶

Create the ideal in ring with given generators.

There are some shorthand notations for creating an ideal, in addition to using the Ideal function:

--  R.ideal(gens, coerce=True)
--  gens*R
--  R*gens

INPUT:

R (optional) - a ring (if not given, will try to infer it from gens)
gens - list of elements generating the ideal
coerce (optional) - bool (default: True); whether gens need to be coerced into ring.

OUTPUT: The ideal of ring generated by gens.

EXAMPLES:

sage: R, x = PolynomialRing(ZZ, 'x').objgen()
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: I
Ideal (x^2 + 3*x + 4, x^2 + 1) of Univariate Polynomial Ring in x over Integer Ring
sage: Ideal(R, [4 + 3*x + x^2, 1 + x^2])
Ideal (x^2 + 3*x + 4, x^2 + 1) of Univariate Polynomial Ring in x over Integer Ring
sage: Ideal((4 + 3*x + x^2, 1 + x^2))
Ideal (x^2 + 3*x + 4, x^2 + 1) of Univariate Polynomial Ring in x over Integer Ring

sage: ideal(x^2-2*x+1, x^2-1)
Ideal (x^2 - 2*x + 1, x^2 - 1) of Univariate Polynomial Ring in x over Integer Ring
sage: ideal([x^2-2*x+1, x^2-1])
Ideal (x^2 - 2*x + 1, x^2 - 1) of Univariate Polynomial Ring in x over Integer Ring
sage: l = [x^2-2*x+1, x^2-1]
sage: ideal(f^2 for f in l)
Ideal (x^4 - 4*x^3 + 6*x^2 - 4*x + 1, x^4 - 2*x^2 + 1) of
Univariate Polynomial Ring in x over Integer Ring

This example illustrates how Sage finds a common ambient ring for the ideal, even though 1 is in the integers (in this case).

sage: R.<t> = ZZ['t']
sage: i = ideal(1,t,t^2)
sage: i
Ideal (1, t, t^2) of Univariate Polynomial Ring in t over Integer Ring
sage: ideal(1/2,t,t^2)
Principal ideal (1) of Univariate Polynomial Ring in t over Rational Field

This shows that the issues at trac #1104 are resolved:

sage: Ideal(3, 5)
Principal ideal (1) of Integer Ring
sage: Ideal(ZZ, 3, 5)
Principal ideal (1) of Integer Ring
sage: Ideal(2, 4, 6)
Principal ideal (2) of Integer Ring

You have to provide enough information that Sage can figure out which ring to put the ideal in.

sage: I = Ideal([])
...
ValueError: unable to determine which ring to embed the ideal in

sage: I = Ideal()
...
ValueError: need at least one argument

TESTS:

sage: R, x = PolynomialRing(ZZ, 'x').objgen()
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: I == loads(dumps(I))
True

sage: I = Ideal(R, [4 + 3*x + x^2, 1 + x^2])
sage: I == loads(dumps(I))
True

sage: I = Ideal((4 + 3*x + x^2, 1 + x^2))
sage: I == loads(dumps(I))
True

This shows that the issue at trac ticket #5477 is fixed:

sage: R.<x> = QQ[]
sage: I = R.ideal([x + x^2])
sage: J = R.ideal([2*x + 2*x^2])
sage: J
Principal ideal (x^2 + x) of Univariate Polynomial Ring in x over Rational Field
sage: S = R.quotient_ring(I)
sage: U = R.quotient_ring(J)
sage: I == J
True
sage: S == U
True

class sage.rings.ideal.Ideal_fractional(ring, gens, coerce=True)¶: Bases: sage.rings.ideal.Ideal_generic

class sage.rings.ideal.Ideal_generic(ring, gens, coerce=True)¶

Bases: sage.structure.element.MonoidElement

An ideal.

apply_morphism(phi)¶

Apply the morphism phi to every element of this ideal. Returns an ideal in the domain of phi.

EXAMPLES:

sage: psi = CC['x'].hom([-CC['x'].0])
sage: J = ideal([CC['x'].0 + 1]); J
Principal ideal (x + 1.00000000000000) of Univariate Polynomial Ring in x over Complex Field with 53 bits of precision
sage: psi(J)
Principal ideal (x - 1.00000000000000) of Univariate Polynomial Ring in x over Complex Field with 53 bits of precision
sage: J.apply_morphism(psi)
Principal ideal (x - 1.00000000000000) of Univariate Polynomial Ring in x over Complex Field with 53 bits of precision

sage: psi = ZZ['x'].hom([-ZZ['x'].0])
sage: J = ideal([ZZ['x'].0, 2]); J
Ideal (x, 2) of Univariate Polynomial Ring in x over Integer Ring
sage: psi(J)
Ideal (-x, 2) of Univariate Polynomial Ring in x over Integer Ring
sage: J.apply_morphism(psi)
Ideal (-x, 2) of Univariate Polynomial Ring in x over Integer Ring

TESTS:

sage: K.<a> = NumberField(x^2 + 1)
sage: A = K.ideal(a)
sage: taus = K.embeddings(K)
sage: A.apply_morphism(taus[0]) # identity
Fractional ideal (a)
sage: A.apply_morphism(taus[1]) # complex conjugation
Fractional ideal (-a)
sage: A.apply_morphism(taus[0]) == A.apply_morphism(taus[1])
True

sage: K.<a> = NumberField(x^2 + 5)
sage: B = K.ideal([2, a + 1]); B
Fractional ideal (2, a + 1)
sage: taus = K.embeddings(K)
sage: B.apply_morphism(taus[0]) # identity
Fractional ideal (2, a + 1)

Since 2 is totally ramified, complex conjugation fixes it:

sage: B.apply_morphism(taus[1]) # complex conjugation
Fractional ideal (2, a + 1)
sage: taus[1](B)
Fractional ideal (2, a + 1)

associated_primes()¶

Return the list of associated prime ideals of this ideal.

EXAMPLES:

sage: R = ZZ[x]
sage: I = R.ideal(7)
sage: I.associated_primes()
...
NotImplementedError

base_ring()¶

Returns the base ring of this ideal.

EXAMPLES:

sage: R = ZZ
sage: I = 3*R; I
Principal ideal (3) of Integer Ring
sage: J = 2*I; J
Principal ideal (6) of Integer Ring
sage: I.base_ring(); J.base_ring()
Integer Ring
Integer Ring

We construct an example of an ideal of a quotient ring:

sage: R = PolynomialRing(QQ, 'x'); x = R.gen()
sage: I = R.ideal(x^2 - 2)
sage: I.base_ring()
Rational Field

And p-adic numbers:

sage: R = Zp(7, prec=10); R
7-adic Ring with capped relative precision 10
sage: I = 7*R; I
Principal ideal (7 + O(7^11)) of 7-adic Ring with capped relative precision 10
sage: I.base_ring()
7-adic Ring with capped relative precision 10

category()¶

Return the category of this ideal.

EXAMPLES:

Note that category is dependent on the ring of the ideal.

sage: I = ZZ.ideal(7)
sage: J = ZZ[x].ideal(7,x)
sage: K = ZZ[x].ideal(7)
sage: I.category()
Category of ring ideals in Integer Ring
sage: J.category()
Category of ring ideals in Univariate Polynomial Ring in x
over Integer Ring
sage: K.category()
Category of ring ideals in Univariate Polynomial Ring in x
over Integer Ring

embedded_primes()¶

Return the list of embedded primes of this ideal.

EXAMPLES:

sage: R.<x, y> = QQ[]
sage: I = R.ideal(x^2, x*y)
sage: I.embedded_primes()
[Ideal (y, x) of Multivariate Polynomial Ring in x, y over Rational Field]

gen(i)¶

Return the i-th generator in the current basis of this ideal.

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQ,2)
sage: I = Ideal([x,y+1]); I
Ideal (x, y + 1) of Multivariate Polynomial Ring in x, y over Rational Field
sage: I.gen(1)
y + 1

sage: ZZ.ideal(5,10).gen()
5

gens()¶

Return a set of generators / a basis of self. This is usually the set of generators provided during object creation.

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQ,2)
sage: I = Ideal([x,y+1]); I
Ideal (x, y + 1) of Multivariate Polynomial Ring in x, y over Rational Field
sage: I.gens()
(x, y + 1)

sage: ZZ.ideal(5,10).gens()
(5,)

gens_reduced()¶

Same as gens() for this ideal, since there is currently no special gens_reduced algorithm implemented for this ring.

This method is provided so that ideals in ZZ have the method gens_reduced(), just like ideals of number fields.

EXAMPLES:

sage: ZZ.ideal(5).gens_reduced()
(5,)

is_maximal()¶

Returns True if the ideal is maximal in the ring containing the ideal.

TODO: Make self.is_maximal() work! Write this code!

EXAMPLES:

sage: R = ZZ
sage: I = R.ideal(7)
sage: I.is_maximal()
...
NotImplementedError

is_primary(P=None)¶

Returns True if this ideal is primary (or $P$ -primary, if a prime ideal $P$ is specified).

Recall that an ideal $I$ is primary if and only if $I$ has a unique associated prime (see page 52 in [AtiMac]). If this prime is $P$ , then $I$ is said to be $P$ -primary.

INPUT:

P - (default: None) a prime ideal in the same ring

EXAMPLES:

sage: R.<x, y> = QQ[]
sage: I = R.ideal([x^2, x*y])
sage: I.is_primary()
False
sage: J = I.primary_decomposition()[1]; J
Ideal (y, x^2) of Multivariate Polynomial Ring in x, y over Rational Field
sage: J.is_primary()
True
sage: J.is_prime()
False

Some examples from the Macaulay2 documentation:

sage: R.<x, y, z> = GF(101)[]
sage: I = R.ideal([y^6])
sage: I.is_primary()
True
sage: I.is_primary(R.ideal([y]))
True
sage: I = R.ideal([x^4, y^7])
sage: I.is_primary()
True
sage: I = R.ideal([x*y, y^2])
sage: I.is_primary()
False

NOTES: Uses the list of associated primes.

REFERENCES:

[AtiMac]

Atiyah and Macdonald, “Introduction to commutative algebra”, Addison-Wesley, 1969.

is_prime()¶

Returns True if the ideal is prime.

EXAMPLES:

sage: R.<x, y> = QQ[]
sage: I = R.ideal([x, y])
sage: I.is_prime()        # a maximal ideal
True
sage: I = R.ideal([x^2-y])
sage: I.is_prime()        # a non-maximal prime ideal
True
sage: I = R.ideal([x^2, y])
sage: I.is_prime()        # a non-prime primary ideal
False
sage: I = R.ideal([x^2, x*y])
sage: I.is_prime()        # a non-prime non-primary ideal
False

Note that this method is not implemented for all rings where it could be:

sage: R = ZZ[x]
sage: I = R.ideal(7)
sage: I.is_prime()        # when implemented, should be True
...
NotImplementedError

NOTES: Uses the list of associated primes.

is_principal()¶

Returns True if the ideal is principal in the ring containing the ideal.

TODO: Code is naive. Only keeps track of ideal generators as set during initialization of the ideal. (Can the base ring change? See example below.)

EXAMPLES:

sage: R = ZZ[x]
sage: I = R.ideal(2,x)
sage: I.is_principal()
...
NotImplementedError
sage: J = R.base_extend(QQ).ideal(2,x)
sage: J.is_principal()
True

is_trivial()¶

Return True if this ideal is (0) or (1).

TESTS:

sage: I = ZZ.ideal(5)
sage: I.is_trivial()
False

sage: I = ZZ['x'].ideal(-1)
sage: I.is_trivial()
True

sage: I = ZZ['x'].ideal(ZZ['x'].gen()^2)
sage: I.is_trivial()
False

sage: I = QQ['x', 'y'].ideal(-5)
sage: I.is_trivial()
True

sage: I = CC['x'].ideal(0)
sage: I.is_trivial()
True

minimal_associated_primes()¶

Return the list of minimal associated prime ideals of this ideal.

EXAMPLES:

sage: R = ZZ[x]
sage: I = R.ideal(7)
sage: I.minimal_associated_primes()
...
NotImplementedError

ngens()¶

Return the number of generators in the basis.

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQ,2)
sage: I = Ideal([x,y+1]); I
Ideal (x, y + 1) of Multivariate Polynomial Ring in x, y over Rational Field
sage: I.ngens()
2

sage: ZZ.ideal(5,10).ngens()
1

primary_decomposition()¶

Return a decomposition of this ideal into primary ideals.

EXAMPLES:

sage: R = ZZ[x]
sage: I = R.ideal(7)
sage: I.primary_decomposition()
...
NotImplementedError

reduce(f)¶

Return the reduction of the element of $f$ modulo the ideal $I$ (=self). This is an element of $R$ that is equivalent modulo $I$ to $f$ .

EXAMPLES:

sage: ZZ.ideal(5).reduce(17)
2
sage: parent(ZZ.ideal(5).reduce(17))
Integer Ring

ring()¶

Returns the ring containing this ideal.

EXAMPLES:

sage: R = ZZ
sage: I = 3*R; I
Principal ideal (3) of Integer Ring
sage: J = 2*I; J
Principal ideal (6) of Integer Ring
sage: I.ring(); J.ring()
Integer Ring
Integer Ring

Note that self.ring() is different from self.base_ring()

sage: R = PolynomialRing(QQ, 'x'); x = R.gen()
sage: I = R.ideal(x^2 - 2)
sage: I.base_ring()
Rational Field
sage: I.ring()
Univariate Polynomial Ring in x over Rational Field

Another example using polynomial rings:

sage: R = PolynomialRing(QQ, 'x'); x = R.gen()
sage: I = R.ideal(x^2 - 3)
sage: I.ring()
Univariate Polynomial Ring in x over Rational Field
sage: Rbar = R.quotient(I, names='a')
sage: S = PolynomialRing(Rbar, 'y'); y = Rbar.gen(); S
Univariate Polynomial Ring in y over Univariate Quotient Polynomial Ring in a over Rational Field with modulus x^2 - 3
sage: J = S.ideal(y^2 + 1)
sage: J.ring()
Univariate Polynomial Ring in y over Univariate Quotient Polynomial Ring in a over Rational Field with modulus x^2 - 3

class sage.rings.ideal.Ideal_pid(ring, gen)¶

Bases: sage.rings.ideal.Ideal_principal

An ideal of a principal ideal domain.

gcd(other)¶

Returns the greatest common divisor of the principal ideal with the ideal other; that is, the largest principal ideal contained in both the ideal and other

TODO: This is not implemented in the case when other is neither principal nor when the generator of self is contained in other. Also, it seems that this class is used only in PIDs–is this redundant? Note: second example is broken.

EXAMPLES:

An example in the principal ideal domain ZZ:

sage: R = ZZ
sage: I = R.ideal(42)
sage: J = R.ideal(70)
sage: I.gcd(J)
Principal ideal (14) of Integer Ring
sage: J.gcd(I)
Principal ideal (14) of Integer Ring

TESTS:

We cannot take the gcd of a principal ideal with a non-principal ideal as well: ( gcd(I,J) should be (7) )

sage: I = ZZ.ideal(7)
sage: J = ZZ[x].ideal(7,x)
sage: I.gcd(J)
...
NotImplementedError
sage: J.gcd(I)
...
AttributeError: 'Ideal_generic' object has no attribute 'gcd'

Note:

sage: type(I)
<class 'sage.rings.ideal.Ideal_pid'>
sage: type(J)
<class 'sage.rings.ideal.Ideal_generic'>

is_prime()¶

Returns True if the ideal is prime. This relies on the ring elements having a method is_irreducible() implemented, since an ideal (a) is prime iff a is irreducible (or 0)

EXAMPLES:

sage: ZZ.ideal(2).is_prime() 
True 
sage: ZZ.ideal(-2).is_prime() 
True 
sage: ZZ.ideal(4).is_prime() 
False
sage: ZZ.ideal(0).is_prime() 
True
sage: R.<x>=QQ[]
sage: P=R.ideal(x^2+1); P
Principal ideal (x^2 + 1) of Univariate Polynomial Ring in x over Rational Field
sage: P.is_prime()
True

reduce(f)¶

Return the reduction of f modulo self.

EXAMPLES:

sage: I = 8*ZZ
sage: I.reduce(10)
2
sage: n = 10; n.mod(I)
2

residue_field()¶

Return the residue class field of this ideal, which must be prime.

TODO: Implement this for more general rings. Currently only defined for ZZ and for number field orders.

EXAMPLES:

sage: P = ZZ.ideal(61); P
Principal ideal (61) of Integer Ring
sage: F = P.residue_field(); F
Residue field of Integers modulo 61
sage: pi = F.reduction_map(); pi
Partially defined reduction map from Rational Field to Residue field of Integers modulo 61
sage: pi(123/234)
6
sage: pi(1/61)
...
ZeroDivisionError: Cannot reduce rational 1/61 modulo 61: it has negative valuation
sage: lift = F.lift_map(); lift
Lifting map from Residue field of Integers modulo 61 to Rational Field
sage: lift(F(12345/67890))
33
sage: (12345/67890) % 61
33

TESTS:

sage: ZZ.ideal(96).residue_field()
...
ValueError: The ideal (Principal ideal (96) of Integer Ring) is not prime

sage: R.<x>=QQ[]
sage: I=R.ideal(x^2+1)
sage: I.is_prime()
True
sage: I.residue_field()
Traceback (most recent call last):
NotImplementedError: residue_field() is only implemented for ZZ and rings of integers of number fields.

class sage.rings.ideal.Ideal_principal(ring, gen)¶

Bases: sage.rings.ideal.Ideal_generic

A principal ideal.

divides(other)¶

Returns True if self divides other.

EXAMPLES:

sage: P.<x> = PolynomialRing(QQ)
sage: I = P.ideal(x)
sage: J = P.ideal(x^2)
sage: I.divides(J)
True
sage: J.divides(I)
False

gen()¶

Returns the generator of the principal ideal. The generators are elements of the ring containing the ideal.

EXAMPLES:

A simple example in the integers:

sage: R = ZZ
sage: I = R.ideal(7)
sage: J = R.ideal(7, 14)
sage: I.gen(); J.gen()
7
7

Note that the generator belongs to the ring from which the ideal was initialized:

sage: R = ZZ[x]
sage: I = R.ideal(x)
sage: J = R.base_extend(QQ).ideal(2,x)
sage: a = I.gen(); a
x
sage: b = J.gen(); b
1
sage: a.base_ring()
Integer Ring
sage: b.base_ring()
Rational Field

is_principal()¶

Returns True if the ideal is principal in the ring containing the ideal. When the ideal construction is explicitly principal (i.e. when we define an ideal with one element) this is always the case.

EXAMPLES:

Note that Sage automatically coerces ideals into principal ideals during initialization:

sage: R = ZZ[x]
sage: I = R.ideal(x)
sage: J = R.ideal(2,x)
sage: K = R.base_extend(QQ).ideal(2,x)
sage: I
Principal ideal (x) of Univariate Polynomial Ring in x
over Integer Ring
sage: J
Ideal (2, x) of Univariate Polynomial Ring in x over Integer Ring
sage: K
Principal ideal (1) of Univariate Polynomial Ring in x
over Rational Field
sage: I.is_principal()
True
sage: K.is_principal()
True

sage.rings.ideal.Katsura(R, n=None, homog=False, singular=Singular)¶

n-th katsura ideal of R if R is coercible to Singular. If n==None n is set to R.ngens()

INPUT:

R - base ring to construct ideal for
n - which katsura ideal of R
homog - if True a homogeneous ideal is returned using the last variable in the ideal (default: False)
singular - singular instance to use

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ,3)
sage: I = sage.rings.ideal.Katsura(P,3); I
Ideal (x + 2*y + 2*z - 1, x^2 + 2*y^2 + 2*z^2 - x, 2*x*y + 2*y*z - y)
of Multivariate Polynomial Ring in x, y, z over Rational Field

sage: Q.<x> = PolynomialRing(QQ,1)
sage: J = sage.rings.ideal.Katsura(Q,1); J
Ideal (x - 1) of Multivariate Polynomial Ring in x over Rational Field

sage.rings.ideal.is_Ideal(x)¶

Returns True if object is an ideal of a ring.

EXAMPLES:

A simple example involving the ring of integers. Note that Sage does not interpret rings objects themselves as ideals. However, one can still explicitly construct these ideals:

sage: from sage.rings.ideal import is_Ideal
sage: R = ZZ
sage: is_Ideal(R)
False
sage: 1*R; is_Ideal(1*R)
Principal ideal (1) of Integer Ring
True
sage: 0*R; is_Ideal(0*R)
Principal ideal (0) of Integer Ring
True

Sage recognizes ideals of polynomial rings as well:

sage: R = PolynomialRing(QQ, 'x'); x = R.gen()
sage: I = R.ideal(x^2 + 1); I
Principal ideal (x^2 + 1) of Univariate Polynomial Ring in x over Rational Field
sage: is_Ideal(I)
True
sage: is_Ideal((x^2 + 1)*R)
True

Ideals¶

Previous topic

Next topic

This Page

Navigation

Ideals¶

Previous topic

Next topic

This Page

Quick search

Navigation