Educational Versions of Groebner Basis Algorithms.¶

Following [BW93] the original Buchberger algorithm (c.f. algorithm GROEBNER in [BW93]) and an improved version of Buchberger’s algorithm (c.g. algorithm GROEBNERNEW2 in [BW93]) are implemented.

No attempt was made to optimize either algorithm as the emphasis of these implementations is a clean and easy presentation. To compute a Groebner basis in Sage efficiently use the sage.rings.polynomial.multi_polynomial_ideal.MPolynomialIdeal.groebner_basis() method on multivariate polynomial objects.

Note

The notion of ‘term’ and ‘monomial’ in [BW93] is swapped from the notion of those words in Sage (or the other way around, however you prefer it). In Sage a term is a monomial multiplied by a coefficient, while in [BW93] a monomial is a term multiplied by a coefficient. Also, what is called LM (the leading monomial) in Sage is called HT (the head term) in [BW93].

EXAMPLES:

Consider Katsura-6 w.r.t. a degrevlex ordering.:

sage: from sage.rings.polynomial.toy_buchberger import *
sage: P.<a,b,c,e,f,g,h,i,j,k> = PolynomialRing(GF(32003),10)
sage: I = sage.rings.ideal.Katsura(P,6)

sage: g1 = buchberger(I)
sage: g2 = buchberger_improved(I)
sage: g3 = I.groebner_basis()

All algorithms actually compute a Groebner basis:

sage: Ideal(g1).basis_is_groebner()
True
sage: Ideal(g2).basis_is_groebner()
True
sage: Ideal(g3).basis_is_groebner()
True

The results are correct:

sage: Ideal(g1) == Ideal(g2) == Ideal(g3)
True

If get_verbose() is 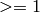$>= 1$ a protocol is provided:

sage: set_verbose(1)
sage: P.<a,b,c> = PolynomialRing(GF(127),3)
sage: I = sage.rings.ideal.Katsura(P)
// sage...              [0]  ideal, 3 generator(s)

sage: I
Ideal (a + 2*b + 2*c - 1, a^2 + 2*b^2 + 2*c^2 - a, 2*a*b + 2*b*c - b) of Multivariate Polynomial Ring in a, b, c over Finite Field of size 127

The original Buchberger algorithm performs 15 useless reductions to zero for this example:

sage: buchberger(I)
(a + 2*b + 2*c - 1, a^2 + 2*b^2 + 2*c^2 - a) => -2*b^2 - 6*b*c - 6*c^2 + b + 2*c
G: set([a + 2*b + 2*c - 1, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c])
<BLANKLINE>
(a^2 + 2*b^2 + 2*c^2 - a, a + 2*b + 2*c - 1) => 0
G: set([a + 2*b + 2*c - 1, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c])
<BLANKLINE>
(a + 2*b + 2*c - 1, 2*a*b + 2*b*c - b) => -5*b*c - 6*c^2 - 63*b + 2*c
G: set([a + 2*b + 2*c - 1, 2*a*b + 2*b*c - b, -5*b*c - 6*c^2 - 63*b + 2*c, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c])
<BLANKLINE>
(2*a*b + 2*b*c - b, a + 2*b + 2*c - 1) => 0
G: set([a + 2*b + 2*c - 1, 2*a*b + 2*b*c - b, -5*b*c - 6*c^2 - 63*b + 2*c, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c])
<BLANKLINE>
(2*a*b + 2*b*c - b, -5*b*c - 6*c^2 - 63*b + 2*c) => -22*c^3 + 24*c^2 - 60*b - 62*c
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(2*a*b + 2*b*c - b, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(a + 2*b + 2*c - 1, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(a^2 + 2*b^2 + 2*c^2 - a, 2*a*b + 2*b*c - b) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(-2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(a + 2*b + 2*c - 1, -5*b*c - 6*c^2 - 63*b + 2*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(a^2 + 2*b^2 + 2*c^2 - a, -5*b*c - 6*c^2 - 63*b + 2*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(-5*b*c - 6*c^2 - 63*b + 2*c, -22*c^3 + 24*c^2 - 60*b - 62*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(-2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -22*c^3 + 24*c^2 - 60*b - 62*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(2*a*b + 2*b*c - b, -22*c^3 + 24*c^2 - 60*b - 62*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
(a^2 + 2*b^2 + 2*c^2 - a, -22*c^3 + 24*c^2 - 60*b - 62*c) => 0
G: set([a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c])
<BLANKLINE>
15 reductions to zero.
[a + 2*b + 2*c - 1, -22*c^3 + 24*c^2 - 60*b - 62*c, 2*a*b + 2*b*c - b, a^2 + 2*b^2 + 2*c^2 - a, -2*b^2 - 6*b*c - 6*c^2 + b + 2*c, -5*b*c - 6*c^2 - 63*b + 2*c]

The ‘improved’ Buchberger algorithm in contrast only performs 3 reductions to zero:

sage: buchberger_improved(I)
(b^2 - 26*c^2 - 51*b + 51*c, b*c + 52*c^2 + 38*b + 25*c) => 11*c^3 - 12*c^2 + 30*b + 31*c
G: set([a + 2*b + 2*c - 1, b^2 - 26*c^2 - 51*b + 51*c, 11*c^3 - 12*c^2 + 30*b + 31*c, b*c + 52*c^2 + 38*b + 25*c])
<BLANKLINE>
(11*c^3 - 12*c^2 + 30*b + 31*c, b*c + 52*c^2 + 38*b + 25*c) => 0
G: set([a + 2*b + 2*c - 1, b^2 - 26*c^2 - 51*b + 51*c, 11*c^3 - 12*c^2 + 30*b + 31*c, b*c + 52*c^2 + 38*b + 25*c])
<BLANKLINE>
1 reductions to zero.
[a + 2*b + 2*c - 1, b^2 - 26*c^2 - 51*b + 51*c, c^3 + 22*c^2 - 55*b + 49*c, b*c + 52*c^2 + 38*b + 25*c]

REFERENCES:

[BW93]

(1, 2, 3, 4, 5, 6, 7, 8, 9) Thomas Becker and Volker Weispfenning. Groebner Bases - A Computational Approach To Commutative Algebra. Springer, New York 1993.

AUTHOR:

Martin Albrecht (2007-05-24): initial version
Marshall Hampton (2009-07-08): some doctest additions

sage.rings.polynomial.toy_buchberger.LCM(f, g)¶

sage.rings.polynomial.toy_buchberger.LM(f)¶

sage.rings.polynomial.toy_buchberger.LT(f)¶

sage.rings.polynomial.toy_buchberger.buchberger(F)¶

The original version of Buchberger’s algorithm as presented in [BW93], page 214.

INPUT:

F - an ideal in a multivariate polynomial ring

OUTPUT:

a Groebner basis for F

Note

The verbosity of this function may be controlled with a set_verbose() call. Any value >=1 will result in this function printing intermediate bases.

EXAMPLES:

sage: from sage.rings.polynomial.toy_buchberger import buchberger
sage: R.<x,y,z> = PolynomialRing(QQ,3)
sage: set_verbose(0)
sage: buchberger(R.ideal([x^2 - z - 1, z^2 - y - 1, x*y^2 - x - 1]))
[-y^3 + x*z - x + y, y^2*z + y^2 - x - z - 1, x*y^2 - x - 1, x^2 - z - 1, z^2 - y - 1]

sage.rings.polynomial.toy_buchberger.buchberger_improved(F)¶

An improved version of Buchberger’s algorithm as presented in [BW93], page 232.

This variant uses the Gebauer-Moeller Installation to apply Buchberger’s first and second criterion to avoid useless pairs.

INPUT:

F - an ideal in a multivariate polynomial ring

OUTPUT:

a Groebner basis for F

Note

The verbosity of this function may be controlled with a set_verbose() call. Any value >=1 will result in this function printing intermediate Groebner bases.

EXAMPLES:

sage: from sage.rings.polynomial.toy_buchberger import buchberger_improved
sage: R.<x,y,z> = PolynomialRing(QQ,3)
sage: set_verbose(0)
sage: buchberger_improved(R.ideal([x^4-y-z,x*y*z-1]))
[x*y*z - 1, x^3 - y^2*z - y*z^2, y^3*z^2 + y^2*z^3 - x^2]

sage.rings.polynomial.toy_buchberger.inter_reduction(Q)¶

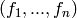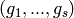If Q is the set $(f_1, ..., f_n)$ this method returns $(g_1, ..., g_s)$ such that:

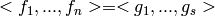
$<f_1,...,f_n> = <g_1,...,g_s>$
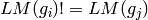$LM(g_i) != LM(g_j)$ for all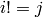 $i != j$
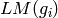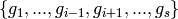
$LM(g_i)$ does not divide $m$ for all monomials $m$ of $\{g_1,...,g_{i-1}, g_{i+1},...,g_s\}$
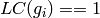$LC(g_i) == 1$ for all $i$ .

INPUT:

Q - a set of polynomials

EXAMPLES:

sage: from sage.rings.polynomial.toy_buchberger import inter_reduction
sage: inter_reduction(set())
set([])

sage: (x,y) = QQ['x,y'].gens()
sage: reduced = inter_reduction(set([x^2-5*y^2,x^3]))
sage: reduced == set([x*y^2, x^2-5*y^2])
True

sage.rings.polynomial.toy_buchberger.select(P)¶

The normal selection strategy

INPUT:

P - a list of critical pairs

OUTPUT:

an element of P

EXAMPLES:

sage: from sage.rings.polynomial.toy_buchberger import select
sage: R.<x,y,z> = PolynomialRing(QQ,3, order='lex')
sage: ps = [x^3 - z -1, z^3 - y - 1, x^5 - y - 2]
sage: pairs = [[ps[i],ps[j]] for i in range(3) for j in range(i+1,3)]
sage: select(pairs)
[x^3 - z - 1, -y + z^3 - 1]

sage.rings.polynomial.toy_buchberger.spol(f, g)¶

Computes the S-polynomial of f and g.

INPUT:

f,g - polynomials

OUTPUT:

The S-polynomial of f and g.

EXAMPLES:

sage: R.<x,y,z> = PolynomialRing(QQ,3)
sage: from sage.rings.polynomial.toy_buchberger import spol
sage: spol(x^2 - z - 1, z^2 - y - 1)
x^2*y - z^3 + x^2 - z^2

sage.rings.polynomial.toy_buchberger.update(G, B, h)¶

Update G using the list of critical pairs B and the polynomial h as presented in [BW93], page 230. For this, Buchberger’s first and second criterion are tested.

This function implements the Gebauer-Moeller Installation.

INPUT:

G - an intermediate Groebner basis
B - a list of critical pairs
h - a polynomial

OUTPUT:

a tuple of an intermediate Groebner basis and a list of critical pairs

EXAMPLES:

sage: from sage.rings.polynomial.toy_buchberger import update
sage: R.<x,y,z> = PolynomialRing(QQ,3)
sage: set_verbose(0)
sage: update(set(),set(),x*y*z)
(set([x*y*z]), set([]))
sage: G,B = update(set(),set(),x*y*z-1)
sage: G,B = update(G,B,x*y^2-1)
sage: G,B
(set([x*y*z - 1, x*y^2 - 1]), set([(x*y^2 - 1, x*y*z - 1)]))

Educational Versions of Groebner Basis Algorithms.¶

Previous topic

Next topic

This Page

Navigation

Educational Versions of Groebner Basis Algorithms.¶

Previous topic

Next topic

This Page

Quick search

Navigation