 -Adic Generic Nodes.¶
-Adic Generic Nodes.¶This file contains a bunch of intermediate classes for the  -adic
parents, allowing a function to be implemented at the right level of
generality.
-adic
parents, allowing a function to be implemented at the right level of
generality.
AUTHORS:
Bases: sage.rings.padics.local_generic.LocalGeneric
Returns whether this  -adic ring bounds precision in a
capped absolute fashion.
-adic ring bounds precision in a
capped absolute fashion.
The absolute precision of an element is the power of  modulo
which that element is defined. In a capped absolute ring, the
absolute precision of elements are bounded by a constant
depending on the ring.
modulo
which that element is defined. In a capped absolute ring, the
absolute precision of elements are bounded by a constant
depending on the ring.
EXAMPLES:
sage: R = ZpCA(5, 15)
sage: R.is_capped_absolute()
True
sage: R(5^7)
5^7 + O(5^15)
sage: S = Zp(5, 15)
sage: S.is_capped_absolute()
False
sage: S(5^7)
5^7 + O(5^22)
Bases: sage.rings.padics.local_generic.LocalGeneric
Returns whether this  -adic ring bounds precision in a capped
relative fashion.
-adic ring bounds precision in a capped
relative fashion.
The relative precision of an element is the power of p modulo which the unit part of that element is defined. In a capped relative ring, the relative precision of elements are bounded by a constant depending on the ring.
EXAMPLES:
sage: R = ZpCA(5, 15)
sage: R.is_capped_relative()
False
sage: R(5^7)
5^7 + O(5^15)
sage: S = Zp(5, 15)
sage: S.is_capped_relative()
True
sage: S(5^7)
5^7 + O(5^22)
Bases: sage.rings.padics.local_generic.LocalGeneric
Returns whether this  -adic ring bounds precision in a fixed
modulus fashion.
-adic ring bounds precision in a fixed
modulus fashion.
The absolute precision of an element is the power of p modulo
which that element is defined. In a fixed modulus ring, the
absolute precision of every element is defined to be the
precision cap of the parent. This means that some operations,
such as division by  , don’t return a well defined answer.
, don’t return a well defined answer.
EXAMPLES:
sage: R = ZpFM(5,15)
sage: R.is_fixed_mod()
True
sage: R(5^7,absprec=9)
5^7 + O(5^15)
sage: S = ZpCA(5, 15)
sage: S.is_fixed_mod()
False
sage: S(5^7,absprec=9)
5^7 + O(5^9)
Returns True if and only if R is a  -adic field.
-adic field.
EXAMPLES:
sage: is_pAdicField(Zp(17))
False
sage: is_pAdicField(Qp(17))
True
Returns True if and only if R is a  -adic ring (not a
field).
-adic ring (not a
field).
EXAMPLES:
sage: is_pAdicRing(Zp(5))
True
sage: is_pAdicRing(RR)
False
Bases: sage.rings.padics.padic_base_generic.pAdicBaseGeneric, sage.rings.padics.generic_nodes.pAdicFieldGeneric
Returns the composite of two subfields of self, i.e., the largest subfield containing both
INPUT:
 -adic field
-adic fieldOUTPUT:
EXAMPLES:
sage: K = Qp(17); K.composite(K, K) is K
True
Returns the functorial construction of self, namely, completion of the rational numbers with respect a given prime.
Also preserves other information that makes this field unique (e.g. precision, rounding, print mode).
EXAMPLE:
sage: K = Qp(17, 8, print_mode='val-unit', print_sep='&')
sage: c, L = K.construction(); L
Rational Field
sage: c(L)
17-adic Field with capped relative precision 8
sage: K == c(L)
True
Returns the subfield generated by the elements in list
INPUT:
 -adic field
-adic fieldOUTPUT:
EXAMPLES:
sage: K = Qp(17); K.subfield([K(17), K(1827)]) is K
True
Returns the number of subfields of self of degree 
INPUT:
 -adic field
-adic fieldOUTPUT:
EXAMPLES:
sage: K = Qp(17)
sage: K.subfields_of_degree(1)
1
Bases: sage.rings.padics.padic_base_generic.pAdicBaseGeneric, sage.rings.padics.generic_nodes.pAdicRingGeneric
Returns the functorial construction of self, namely, completion of the rational numbers with respect a given prime.
Also preserves other information that makes this field unique (e.g. precision, rounding, print mode).
EXAMPLE:
sage: K = Zp(17, 8, print_mode='val-unit', print_sep='&')
sage: c, L = K.construction(); L
Integer Ring
sage: c(L)
17-adic Ring with capped relative precision 8
sage: K == c(L)
True
Returns a random element of self, optionally using the algorithm argument to decide how it generates the element. Algorithms currently implemented:
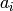 ,
, 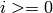 , randomly between
, randomly between  and
and
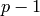 until a nonzero choice is made. Then continue choosing
until a nonzero choice is made. Then continue choosing
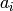 randomly between
randomly between  and
and 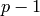 until we reach
precision_cap, and return
until we reach
precision_cap, and return 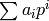 .
.EXAMPLES:
sage: Zp(5,6).random_element()
3 + 3*5 + 2*5^2 + 3*5^3 + 2*5^4 + 5^5 + O(5^6)
sage: ZpCA(5,6).random_element()
4*5^2 + 5^3 + O(5^6)
sage: ZpFM(5,6).random_element()
2 + 4*5^2 + 2*5^4 + 5^5 + O(5^6)
Bases: sage.rings.padics.padic_generic.pAdicGeneric, sage.rings.ring.EuclideanDomain
Returns whether this ring is actually a field, ie False.
EXAMPLES:
sage: Zp(5).is_field()
False
Returns the Krull dimension of self, i.e. 1
INPUT:
 -adic ring
-adic ringOUTPUT:
 -adic ring,
this is 1.
-adic ring,
this is 1.EXAMPLES:
sage: Zp(5).krull_dimension()
1