-Adic Base Generic.

A superclass for implementations of and .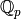

AUTHORS:

• David Roe

class sage.rings.padics.padic_base_generic.pAdicBaseGeneric(p, prec, print_mode, names, element_class)

Bases: sage.rings.padics.padic_generic.pAdicGeneric

absolute_discriminant()

Returns the absolute discriminant of this -adic ring

EXAMPLES:

sage: Zp(5).absolute_discriminant()
1

discriminant(K=None)

Returns the discriminant of this -adic ring over K

INPUT:

• self – a -adic ring
• K – a sub-ring of self or None (default: None)

OUTPUT:

• integer – the discriminant of this ring over K (or the absolute discriminant if K is None)

EXAMPLES:

sage: Zp(5).discriminant()
1

fraction_field(print_mode=None)

Returns the fraction field of self.

INPUT:

• print_mode - a dictionary containing print options. Defaults to the same options as this ring.

OUTPUT:

• the fraction field of self.

EXAMPLES:

sage: R = Zp(5, print_mode='digits')
sage: K = R.fraction_field(); repr(K(1/3))[3:]
'31313131313131313132'
sage: L = R.fraction_field({'max_ram_terms':4}); repr(L(1/3))[3:]
'3132'

gen(n=0)

Returns the nth generator of this extension. For base rings/fields, we consider the generator to be the prime.

EXAMPLES:

sage: R = Zp(5); R.gen()
5 + O(5^21)

has_pth_root()

Returns whether or not has a primitive 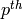root of unity.

EXAMPLES:

sage: Zp(2).has_pth_root()
True
sage: Zp(17).has_pth_root()
False

has_root_of_unity(n)

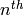Returns whether or not has a primitive root of unity.

INPUT:

• self – a -adic ring
• n – an integer

OUTPUT:

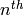• boolean – whether self has primitive root of unity

EXAMPLES:

sage: R=Zp(37)
sage: R.has_root_of_unity(12)
True
sage: R.has_root_of_unity(11)
False

integer_ring(print_mode=None)

Returns the integer ring of self, possibly with print_mode changed.

INPUT:

• print_mode - a dictionary containing print options. Defaults to the same options as this ring.

OUTPUT:

• The ring of integral elements in self.

EXAMPLES:

sage: K = Qp(5, print_mode='digits')
sage: R = K.integer_ring(); repr(R(1/3))[3:]
'31313131313131313132'
sage: S = K.integer_ring({'max_ram_terms':4}); repr(S(1/3))[3:]
'3132'

is_abelian()

Returns whether the Galois group is abelian, i.e. True. #should this be automorphism group?

EXAMPLES:

sage: R = Zp(3, 10,'fixed-mod'); R.is_abelian()
True

is_isomorphic(ring)

Returns whether self and ring are isomorphic, i.e. whether ring is an implementation of for the same prime as self.

INPUT:

• self – a -adic ring
• ring – a ring

OUTPUT:

• boolean – whether ring is an implementation of mathbb{Z}_p` for the same prime as self.

EXAMPLES:

sage: R = Zp(5, 15, print_mode='digits'); S = Zp(5, 44, print_max_terms=4); R.is_isomorphic(S)
True

is_normal()

Returns whether or not this is a normal extension, i.e. True.

EXAMPLES:

sage: R = Zp(3, 10,'fixed-mod'); R.is_normal()
True

plot(max_points=2500, **args)

Creates a visualization of this -adic ring as a fractal similar as a generalization of the the Sierpi’nski triangle. The resulting image attempts to capture the algebraic and topological characteristics of .

INPUT:

• point_count – the maximum number or points to plot, which controls the depth of recursion (default 2500)
• **args – color, size, etc. that are passed to the underlying point graphics objects

REFERENCES:

• Cuoco, A. ‘’Visualizing the -adic Integers’‘, The American Mathematical Monthly, Vol. 98, No. 4 (Apr., 1991), pp. 355-364

EXAMPLES:

sage: Zp(3).plot()
sage: Zp(5).plot(max_points=625)
sage: Zp(23).plot(rgbcolor=(1,0,0))

uniformizer()

Returns a uniformizer for this ring.

EXAMPLES:

sage: R = Zp(3,5,'fixed-mod', 'series')
sage: R.uniformizer()
3 + O(3^5)

uniformizer_pow(n)

Returns the nth power of the uniformizer of self (as an element of self).

EXAMPLES:

sage: R = Zp(5)
sage: R.uniformizer_pow(5)
5^5 + O(5^25)
sage: R.uniformizer_pow(infinity)
0

zeta(n=None)

Returns a generator of the group of roots of unity.

INPUT:

• self – a -adic ring
• n – an integer or None (default: None)

OUTPUT:

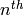• element – a generator of the roots of unity, or a generator of the full group of roots of unity if n is None

EXAMPLES:

sage: R = Zp(37,5)
sage: R.zeta(12)
8 + 24*37 + 37^2 + 29*37^3 + 23*37^4 + O(37^5)

zeta_order()

Returns the order of the group of roots of unity.

EXAMPLES:

sage: R = Zp(37); R.zeta_order()
36
sage: Zp(2).zeta_order()
2