Local Generic.¶

Superclass for $p$ -adic and power series rings.

AUTHORS:

David Roe

class sage.rings.padics.local_generic.LocalGeneric(base, prec, names, element_class)¶

Bases: sage.rings.ring.CommutativeRing

defining_polynomial(var='x')¶

Returns the defining polynomial of this local ring, i.e. just x.

INPUT:

self – a local ring
var – string (default: 'x') the name of the variable

OUTPUT:

- polynomial -- the defining polynomial of this ring as an extension over its ground ring

EXAMPLES:

sage: R = Zp(3, 3, 'fixed-mod'); R.defining_polynomial('foo')
(1 + O(3^3))*foo

degree()¶

Returns the degree of self over the ground ring, i.e. 1.

INPUT:

self – a local ring

OUTPUT:

integer – the degree of this ring, i.e., 1

EXAMPLES:

sage: R = Zp(3, 10, 'capped-rel'); R.degree()
1

e(K=None)¶

Returns the ramification index over the ground ring: 1 unless overridden.

INPUT:

self – a local ring
K – a subring of self (default None)

OUTPUT:

integer – the ramification index of this ring: 1 unless overridden.

EXAMPLES:

sage: R = Zp(3, 5, 'capped-rel'); R.e()
1

ext(*args, **kwds)¶

Constructs an extension of self. See extension for more details.

EXAMPLES:

sage: A = Zp(7,10)
sage: S.<x> = A[]
sage: B.<t> = A.ext(x^2+7)
sage: B.uniformiser()
t + O(t^21)

f(K=None)¶

Returns the inertia degree over the ground ring: 1 unless overridden.

INPUT:

self – a local ring
K – a subring (default None)

OUTPUT:

integer – the inertia degree of this ring: 1 unless overridden.

EXAMPLES:

sage: R = Zp(3, 5, 'capped-rel'); R.f()
1

ground_ring()¶

Returns self.

Will be overridden by extensions.

INPUT:

self – a local ring

OUTPUT:

- the ground ring of ``self``, i.e., itself

EXAMPLES:

sage: R = Zp(3, 5, 'fixed-mod')
sage: S = Zp(3, 4, 'fixed-mod')
sage: R.ground_ring() is R
True
sage: S.ground_ring() is R
False

ground_ring_of_tower()¶

Returns self.

Will be overridden by extensions.

INPUT:

self – a $p$ -adic ring

OUTPUT:

the ground ring of the tower for self, i.e., itself

EXAMPLES:

sage: R = Zp(5)
sage: R.ground_ring_of_tower()
5-adic Ring with capped relative precision 20

inertia_degree(K=None)¶

Returns the inertia degree over K (defaults to the ground ring): 1 unless overridden.

INPUT:

self – a local ring
K – a subring of self (default None)

OUTPUT:

integer – the inertia degree of this ring: 1 unless overridden.

EXAMPLES:

sage: R = Zp(3, 5, 'capped-rel'); R.inertia_degree()
1

inertia_subring()¶

Returns the inertia subring, i.e. self.

INPUT:

self – a local ring

OUTPUT:

the inertia subring of self, i.e., itself

EXAMPLES:

sage: R = Zp(5)
sage: R.inertia_subring()
5-adic Ring with capped relative precision 20

is_atomic_repr()¶

Return False, since we want $p$ -adics to be printed with parentheses around them when they are coefficients, e.g., in a polynomial.

INPUT:

self – a $p$ -adic ring

OUTPUT:

boolean – whether self‘s representation is atomic, i.e., False

EXAMPLES:

sage: R = Zp(5, 5, 'fixed-mod'); R.is_atomic_repr()
False

is_capped_absolute()¶

Returns whether this $p$ -adic ring bounds precision in a capped absolute fashion.

The absolute precision of an element is the power of $p$ modulo which that element is defined. In a capped absolute ring, the absolute precision of elements are bounded by a constant depending on the ring.

EXAMPLES:

sage: R = ZpCA(5, 15)
sage: R.is_capped_absolute()
True
sage: R(5^7)
5^7 + O(5^15)
sage: S = Zp(5, 15)
sage: S.is_capped_absolute()
False
sage: S(5^7)
5^7 + O(5^22)

is_capped_relative()¶

Returns whether this $p$ -adic ring bounds precision in a capped relative fashion.

The relative precision of an element is the power of $p$ modulo which the unit part of that element is defined. In a capped relative ring, the relative precision of elements are bounded by a constant depending on the ring.

EXAMPLES:

sage: R = ZpCA(5, 15)
sage: R.is_capped_relative()
False
sage: R(5^7)
5^7 + O(5^15)
sage: S = Zp(5, 15)
sage: S.is_capped_relative()
True
sage: S(5^7)
5^7 + O(5^22)

is_exact()¶

Returns whether this p-adic ring is exact, i.e. False.

INPUT:: self – a p-adic ring
OUTPUT:: boolean – whether self is exact, i.e. False.
EXAMPLES:: #sage: R = Zp(5, 3, ‘lazy’); R.is_exact() #False sage: R = Zp(5, 3, ‘fixed-mod’); R.is_exact() False

is_finite()¶

Returns whether this ring is finite, i.e. False.

INPUT:

- ``self`` -- a `p`-adic ring

OUTPUT:

- boolean -- whether self is finite, i.e., ``False``

EXAMPLES:

sage: R = Zp(3, 10,'fixed-mod'); R.is_finite()
False

is_fixed_mod()¶

Returns whether this $p$ -adic ring bounds precision in a fixed modulus fashion.

The absolute precision of an element is the power of $p$ modulo which that element is defined. In a fixed modulus ring, the absolute precision of every element is defined to be the precision cap of the parent. This means that some operations, such as division by $p$ , don’t return a well defined answer.

EXAMPLES:

sage: R = ZpFM(5,15)
sage: R.is_fixed_mod()
True
sage: R(5^7,absprec=9)
5^7 + O(5^15)
sage: S = ZpCA(5, 15)
sage: S.is_fixed_mod()
False
sage: S(5^7,absprec=9)
5^7 + O(5^9)

is_lazy()¶

Returns whether this $p$ -adic ring bounds precision in a lazy fashion.

In a lazy ring, elements have mechanisms for computing themselves to greater precision.

EXAMPLES:

sage: R = Zp(5)
sage: R.is_lazy()
False

maximal_unramified_subextension()¶

Returns the maximal unramified subextension.

INPUT:

self – a local ring

OUTPUT:

the maximal unramified subextension of self

EXAMPLES:

sage: R = Zp(5)
sage: R.maximal_unramified_subextension()
5-adic Ring with capped relative precision 20

precision_cap()¶

Returns the precision cap for self.

INPUT:

self – a local ring

OUTPUT:

integer – self‘s precision cap

EXAMPLES:

sage: R = Zp(3, 10,'fixed-mod'); R.precision_cap()
10
sage: R = Zp(3, 10,'capped-rel'); R.precision_cap()
10      
sage: R = Zp(3, 10,'capped-abs'); R.precision_cap()
10

NOTES:

This will have different meanings depending on the type of
local ring.  For fixed modulus rings, all elements are
considered modulo ``self.prime()^self.precision_cap()``.
For rings with an absolute cap (i.e. the class
``pAdicRingCappedAbsolute``), each element has a precision
that is tracked and is bounded above by
``self.precision_cap()``.  Rings with relative caps
(e.g. the class ``pAdicRingCappedRelative``) are the same
except that the precision is the precision of the unit
part of each element.  For lazy rings, this gives the
initial precision to which elements are computed.

ramification_index(K=None)¶

Returns the ramification index over the ground ring: 1 unless overridden.

INPUT:

self – a local ring

OUTPUT:

integer – the ramification index of this ring: 1 unless overridden.

EXAMPLES:

sage: R = Zp(3, 5, 'capped-rel'); R.ramification_index()
1

residue_characteristic()¶

Returns the characteristic of self‘s residue field.

INPUT:

self – a p-adic ring.

OUTPUT:

integer – the characteristic of the residue field.

EXAMPLES:

sage: R = Zp(3, 5, 'capped-rel'); R.residue_characteristic()
3

residue_class_degree(K=None)¶

Returns the inertia degree over the ground ring: 1 unless overridden.

INPUT:

self – a local ring
K – a subring (default None)

OUTPUT:

integer – the inertia degree of this ring: 1 unless overridden.

EXAMPLES:

sage: R = Zp(3, 5, 'capped-rel'); R.residue_class_degree()
1

uniformiser()¶

Returns a uniformiser for self, ie a generator for the unique maximal ideal.

EXAMPLES:

sage: R = Zp(5)
sage: R.uniformiser()
5 + O(5^21)
sage: A = Zp(7,10)
sage: S.<x> = A[]
sage: B.<t> = A.ext(x^2+7)
sage: B.uniformiser()
t + O(t^21)

uniformiser_pow(n)¶

Returns the 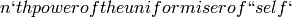$n`th power of the uniformiser of ``self`$ (as an element of self).

EXAMPLES:

sage: R = Zp(5)
sage: R.uniformiser_pow(5)
5^5 + O(5^25)

Local Generic.¶

Previous topic

Next topic

This Page

Navigation

Local Generic.¶

Previous topic

Next topic

This Page

Quick search

Navigation