Laurent Series Rings

EXAMPLES:

sage: R = LaurentSeriesRing(QQ, "x")
sage: R.base_ring()
Rational Field
sage: S = LaurentSeriesRing(GF(17)['x'], 'y')
sage: S
Laurent Series Ring in y over Univariate Polynomial Ring in x over
Finite Field of size 17
sage: S.base_ring()
Univariate Polynomial Ring in x over Finite Field of size 17

sage.rings.laurent_series_ring.LaurentSeriesRing(base_ring, name=None, names=None, sparse=False)

EXAMPLES:

sage: R = LaurentSeriesRing(QQ, 'x'); R
Laurent Series Ring in x over Rational Field
sage: x = R.0
sage: g = 1 - x + x^2 - x^4 +O(x^8); g
1 - x + x^2 - x^4 + O(x^8)
sage: g = 10*x^(-3) + 2006 - 19*x + x^2 - x^4 +O(x^8); g
10*x^-3 + 2006 - 19*x + x^2 - x^4 + O(x^8)

You can also use more mathematical notation when the base is a field:

sage: Frac(QQ[['x']])
Laurent Series Ring in x over Rational Field
sage: Frac(GF(5)['y'])
Fraction Field of Univariate Polynomial Ring in y over Finite Field of size 5

Here the fraction field is not just the Laurent series ring, so you can’t use the Frac notation to make the Laurent series ring.

sage: Frac(ZZ[['t']])
Fraction Field of Power Series Ring in t over Integer Ring

Laurent series rings are determined by their variable and the base ring, and are globally unique.

sage: K = Qp(5, prec = 5)
sage: L = Qp(5, prec = 200)
sage: R.<x> = LaurentSeriesRing(K)
sage: S.<y> = LaurentSeriesRing(L)
sage: R is S
False
sage: T.<y> = LaurentSeriesRing(Qp(5,prec=200))
sage: S is T
True
sage: W.<y> = LaurentSeriesRing(Qp(5,prec=199))
sage: W is T
False

class sage.rings.laurent_series_ring.LaurentSeriesRing_domain(base_ring, name=None, sparse=False)

Bases: sage.rings.laurent_series_ring.LaurentSeriesRing_generic, sage.rings.ring.IntegralDomain

class sage.rings.laurent_series_ring.LaurentSeriesRing_field(base_ring, name=None, sparse=False)

Bases: sage.rings.laurent_series_ring.LaurentSeriesRing_generic, sage.rings.ring.Field

class sage.rings.laurent_series_ring.LaurentSeriesRing_generic(base_ring, name=None, sparse=False)

Bases: sage.rings.ring.CommutativeRing

Univariate Laurent Series Ring

EXAMPLES:

sage: K, q = LaurentSeriesRing(CC, 'q').objgen(); K
Laurent Series Ring in q over Complex Field with 53 bits of precision
sage: loads(K.dumps()) == K
True

base_extend(R)

Returns the laurent series ring over R in the same variable as self, assuming there is a canonical coerce map from the base ring of self to R.

change_ring(R)

characteristic()

default_prec()

gen(n=0)

is_dense()

is_exact()

is_field(proof=True)

is_sparse()

ngens()

power_series_ring()

If this is the Laurent series ring 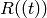, return the power series ring .

EXAMPLES:

sage: R = LaurentSeriesRing(QQ, "x")
sage: R.power_series_ring()
Power Series Ring in x over Rational Field

set_default_prec(n)

sage.rings.laurent_series_ring.is_LaurentSeriesRing(x)