Laurent Series

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(GF(7), 't'); R
Laurent Series Ring in t over Finite Field of size 7
sage: f = 1/(1-t+O(t^10)); f
1 + t + t^2 + t^3 + t^4 + t^5 + t^6 + t^7 + t^8 + t^9 + O(t^10)

Laurent series are immutable:

sage: f[2]
1
sage: f[2] = 5
...
IndexError: Laurent series are immutable    

We compute with a Laurent series over the complex mpfr numbers.

sage: K.<q> = Frac(CC[['q']])
sage: K
Laurent Series Ring in q over Complex Field with 53 bits of precision
sage: q
1.00000000000000*q

Saving and loading.

sage: loads(q.dumps()) == q
True
sage: loads(K.dumps()) == K
True

IMPLEMENTATION: Laurent series in Sage are represented internally as a power of the variable times the unit part (which need not be a unit - it’s a polynomial with nonzero constant term). The zero Laurent series has unit part 0.

AUTHORS:

• William Stein: original version
• David Joyner (2006-01-22): added examples
• Robert Bradshaw (2007-04): optimizations, shifting
• Robert Bradshaw: Cython version

class sage.rings.laurent_series_ring_element.LaurentSeries

Bases: sage.structure.element.AlgebraElement

A Laurent Series.

add_bigoh(prec)

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(QQ)
sage: f = t^2 + t^3 + O(t^10); f
t^2 + t^3 + O(t^10)
sage: f.add_bigoh(5)
t^2 + t^3 + O(t^5)

change_ring(R)

coefficients()

Return the nonzero coefficients of self.

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(QQ)
sage: f = -5/t^(2) + t + t^2 - 10/3*t^3
sage: f.coefficients()
[-5, 1, 1, -10/3]

common_prec(f)

Returns minimum precision of and self.

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(QQ)

sage: f = t^(-1) + t + t^2 + O(t^3)
sage: g = t + t^3 + t^4 + O(t^4)
sage: f.common_prec(g)
3
sage: g.common_prec(f)
3

sage: f = t + t^2 + O(t^3)
sage: g = t^(-3) + t^2
sage: f.common_prec(g)
3
sage: g.common_prec(f)
3

sage: f = t + t^2
sage: f = t^2
sage: f.common_prec(g)
+Infinity

sage: f = t^(-3) + O(t^(-2))
sage: g = t^(-5) + O(t^(-1))
sage: f.common_prec(g)
-2

degree()

Return the degree of a polynomial equivalent to this power series modulo big oh of the precision.

EXAMPLES:

sage: x = Frac(QQ[['x']]).0
sage: g = x^2 - x^4 + O(x^8)
sage: g.degree()
4
sage: g = -10/x^5 + x^2 - x^4 + O(x^8)
sage: g.degree()
4

derivative(*args)

The formal derivative of this Laurent series, with respect to variables supplied in args.

Multiple variables and iteration counts may be supplied; see documentation for the global derivative() function for more details.

See also

_derivative()

EXAMPLES:

sage: R.<x> = LaurentSeriesRing(QQ)
sage: g = 1/x^10 - x + x^2 - x^4 + O(x^8)
sage: g.derivative()
-10*x^-11 - 1 + 2*x - 4*x^3 + O(x^7)
sage: g.derivative(x)
-10*x^-11 - 1 + 2*x - 4*x^3 + O(x^7)

sage: R.<t> = PolynomialRing(ZZ)
sage: S.<x> = LaurentSeriesRing(R)
sage: f = 2*t/x + (3*t^2 + 6*t)*x + O(x^2)
sage: f.derivative()
-2*t*x^-2 + (3*t^2 + 6*t) + O(x)
sage: f.derivative(x)
-2*t*x^-2 + (3*t^2 + 6*t) + O(x)
sage: f.derivative(t)
2*x^-1 + (6*t + 6)*x + O(x^2)

exponents()

Return the exponents appearing in self with nonzero coefficients.

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(QQ)
sage: f = -5/t^(2) + t + t^2 - 10/3*t^3
sage: f.exponents()
[-2, 1, 2, 3]

integral()

The formal integral of this Laurent series with 0 constant term.

EXAMPLES: The integral may or may not be defined if the base ring is not a field.

sage: t = LaurentSeriesRing(ZZ, 't').0
sage: f = 2*t^-3 + 3*t^2 + O(t^4)
sage: f.integral()
-t^-2 + t^3 + O(t^5)

sage: f = t^3
sage: f.integral()
...
ArithmeticError: Coefficients of integral cannot be coerced into the base ring

The integral of 1/t is 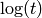, which is not given by a Laurent series:

sage: t = Frac(QQ[['t']]).0
sage: f = -1/t^3 - 31/t + O(t^3)
sage: f.integral()
...
ArithmeticError: The integral of is not a Laurent series, since t^-1 has nonzero coefficient.

Another example with just one negative coefficient:

sage: A.<t> = QQ[[]]
sage: f = -2*t^(-4) + O(t^8)
sage: f.integral()
2/3*t^-3 + O(t^9)
sage: f.integral().derivative() == f
True

is_unit()

Returns True if this is Laurent series is a unit in this ring.

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(QQ)
sage: (2+t).is_unit()
True
sage: f = 2+t^2+O(t^10); f.is_unit()
True
sage: 1/f
1/2 - 1/4*t^2 + 1/8*t^4 - 1/16*t^6 + 1/32*t^8 + O(t^10)
sage: R(0).is_unit()
False
sage: R.<s> = LaurentSeriesRing(ZZ)
sage: f = 2 + s^2 + O(s^10)
sage: f.is_unit()
False
sage: 1/f
...
ArithmeticError: division not defined

ALGORITHM: A Laurent series is a unit if and only if its “unit part” is a unit.

is_zero()

EXAMPLES:

sage: x = Frac(QQ[['x']]).0
sage: f = 1/x + x + x^2 + 3*x^4 + O(x^7)
sage: f.is_zero()
0
sage: z = 0*f
sage: z.is_zero()
1

list()

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(QQ)
sage: f = -5/t^(2) + t + t^2 - 10/3*t^3
sage: f.list()
[-5, 0, 0, 1, 1, -10/3]

power_series()

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(ZZ)
sage: f = 1/(1-t+O(t^10)); f.parent()
Laurent Series Ring in t over Integer Ring
sage: g = f.power_series(); g
1 + t + t^2 + t^3 + t^4 + t^5 + t^6 + t^7 + t^8 + t^9 + O(t^10)
sage: parent(g)
Power Series Ring in t over Integer Ring
sage: f = 3/t^2 +  t^2 + t^3 + O(t^10)
sage: f.power_series()
...
ArithmeticError: self is a not a power series

prec()

This function returns the n so that the Laurent series is of the form (stuff) + 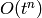. It doesn’t matter how many negative powers appear in the expansion. In particular, prec could be negative.

EXAMPLES:

sage: x = Frac(QQ[['x']]).0
sage: f = x^2 + 3*x^4 + O(x^7)
sage: f.prec()
7
sage: g = 1/x^10 - x + x^2 - x^4 + O(x^8)
sage: g.prec()
8

shift(k)

Returns this laurent series multiplied by the power 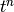. Does not change this series.

Note

Despite the fact that higher order terms are printed to the right in a power series, right shifting decreases the powers of , while left shifting increases them. This is to be consistent with polynomials, integers, etc.

EXAMPLES:

sage: R.<t> = LaurentSeriesRing(QQ['y'])
sage: f = (t+t^-1)^4; f
t^-4 + 4*t^-2 + 6 + 4*t^2 + t^4
sage: f.shift(10)
t^6 + 4*t^8 + 6*t^10 + 4*t^12 + t^14
sage: f >> 10
t^-14 + 4*t^-12 + 6*t^-10 + 4*t^-8 + t^-6
sage: t << 4
t^5
sage: t + O(t^3) >> 4
t^-3 + O(t^-1)

AUTHORS:

• Robert Bradshaw (2007-04-18)

truncate(n)

Returns the laurent series of degree ` < n` which is equivalent to self modulo .

truncate_neg(n)

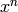Returns the laurent series equivalent to self except without any degree n terms.

This is equivalent to `self - self.truncate(n)`.

valuation()

EXAMPLES:

sage: x = Frac(QQ[['x']]).0
sage: f = 1/x + x^2 + 3*x^4 + O(x^7)
sage: g = 1 - x + x^2 - x^4 + O(x^8)
sage: f.valuation()
-1
sage: g.valuation()
0

valuation_zero_part()

EXAMPLES:

sage: x = Frac(QQ[['x']]).0
sage: f = x + x^2 + 3*x^4 + O(x^7)
sage: f/x
1 + x + 3*x^3 + O(x^6)
sage: f.valuation_zero_part()
1 + x + 3*x^3 + O(x^6)
sage: g = 1/x^7 - x + x^2 - x^4 + O(x^8)
sage: g.valuation_zero_part()
1 - x^8 + x^9 - x^11 + O(x^15)

variable()

EXAMPLES:

sage: x = Frac(QQ[['x']]).0
sage: f = 1/x + x^2 + 3*x^4 + O(x^7)
sage: f.variable()
'x'

sage.rings.laurent_series_ring_element.is_LaurentSeries(x)

sage.rings.laurent_series_ring_element.make_element_from_parent(parent, *args)