 of integers¶
of integers¶AUTHORS:
EXAMPLES:
Add 2 integers:
sage: a = Integer(3) ; b = Integer(4)
sage: a + b == 7
True
Add an integer and a real number:
sage: a + 4.0
7.00000000000000
Add an integer and a rational number:
sage: a + Rational(2)/5
17/5
Add an integer and a complex number:
sage: b = ComplexField().0 + 1.5
sage: loads((a+b).dumps()) == a+b
True
sage: z = 32
sage: -z
-32
sage: z = 0; -z
0
sage: z = -0; -z
0
sage: z = -1; -z
1
Multiplication:
sage: a = Integer(3) ; b = Integer(4)
sage: a * b == 12
True
sage: loads((a * 4.0).dumps()) == a*b
True
sage: a * Rational(2)/5
6/5
sage: list([2,3]) * 4
[2, 3, 2, 3, 2, 3, 2, 3]
sage: 'sage'*Integer(3)
'sagesagesage'
COERCIONS: Returns version of this integer in the multi-precision floating real field R.
sage: n = 9390823
sage: RR = RealField(200)
sage: RR(n)
9.3908230000000000000000000000000000000000000000000000000000e6
Return the GCD of a list v of integers. Elements of v are converted to Sage integers if they aren’t already.
This function is used, e.g., by rings/arith.py
INPUT:
OUTPUT: integer
EXAMPLES:
sage: from sage.rings.integer import GCD_list
sage: w = GCD_list([3,9,30]); w
3
sage: type(w)
<type 'sage.rings.integer.Integer'>
Check that the bug reported in trac #3118 has been fixed:
sage: sage.rings.integer.GCD_list([2,2,3])
1
The inputs are converted to Sage integers.
sage: w = GCD_list([int(3), int(9), '30']); w
3
sage: type(w)
<type 'sage.rings.integer.Integer'>
Bases: sage.structure.element.EuclideanDomainElement
The Integer class represents arbitrary precision integers. It derives from the Element class, so integers can be used as ring elements anywhere in Sage.
Integer() interprets numbers and strings that begin with 0 as octal numbers, and numbers and strings that begin with 0x as hexadecimal numbers.
The class Integer is implemented in Cython, as a wrapper of the GMP mpz_t integer type.
EXAMPLES:
sage: Integer(010)
8
sage: Integer(0x10)
16
sage: Integer(10)
10
sage: Integer('0x12')
18
sage: Integer('012')
10
Return the additive order of self.
EXAMPLES:
sage: ZZ(0).additive_order()
1
sage: ZZ(1).additive_order()
+Infinity
Return the binary digits of self as a string.
EXAMPLES:
sage: print Integer(15).binary()
1111
sage: print Integer(16).binary()
10000
sage: print Integer(16938402384092843092843098243).binary()
1101101011101100011110001110010010100111010001101010001111111000101000000000101111000010000011
Return the bits in self as a list, least significant first.
EXAMPLES:
sage: 500.bits()
[0, 0, 1, 0, 1, 1, 1, 1, 1]
sage: 11.bits()
[1, 1, 0, 1]
Return the ceiling of self, which is self since self is an integer.
EXAMPLES:
sage: n = 6
sage: n.ceil()
6
Return the complex conjugate of this integer, which is the integer itself.
Return the positive integers 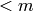 that are coprime to
self.
that are coprime to
self.
EXAMPLES:
sage: n = 8
sage: n.coprime_integers(8)
[1, 3, 5, 7]
sage: n.coprime_integers(11)
[1, 3, 5, 7, 9]
sage: n = 5; n.coprime_integers(10)
[1, 2, 3, 4, 6, 7, 8, 9]
sage: n.coprime_integers(5)
[1, 2, 3, 4]
sage: n = 99; n.coprime_integers(99)
[1, 2, 4, 5, 7, 8, 10, 13, 14, 16, 17, 19, 20, 23, 25, 26, 28, 29, 31, 32, 34, 35, 37, 38, 40, 41, 43, 46, 47, 49, 50, 52, 53, 56, 58, 59, 61, 62, 64, 65, 67, 68, 70, 71, 73, 74, 76, 79, 80, 82, 83, 85, 86, 89, 91, 92, 94, 95, 97, 98]
AUTHORS:
ALGORITHM: Naive - compute lots of GCD’s. If this isn’t good enough for you, please code something better and submit a patch.
Return the unique integer between  and
and 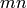 that
is congruent to the integer modulo
that
is congruent to the integer modulo  and to
and to  modulo
modulo  . We assume that
. We assume that  and
and  are
coprime.
are
coprime.
EXAMPLES:
sage: n = 17
sage: m = n.crt(5, 23, 11); m
247
sage: m%23
17
sage: m%11
5
Return the denominator of this integer.
EXAMPLES:
sage: x = 5
sage: x.denominator()
1
sage: x = 0
sage: x.denominator()
1
Return a list of digits for self in the given base in little endian order.
The returned value is unspecified if self is a negative number and the digits are given.
INPUT:
As a shorthand for digits(2), you can use bits().
Also see ndigits().
EXAMPLES:
sage: 17.digits()
[7, 1]
sage: 5.digits(base=2, digits=["zero","one"])
['one', 'zero', 'one']
sage: 5.digits(3)
[2, 1]
sage: 0.digits(base=10) # 0 has 0 digits
[]
sage: 0.digits(base=2) # 0 has 0 digits
[]
sage: 10.digits(16,'0123456789abcdef')
['a']
sage: 0.digits(16,'0123456789abcdef')
[]
sage: 0.digits(16,'0123456789abcdef',padto=1)
['0']
sage: 123.digits(base=10,padto=5)
[3, 2, 1, 0, 0]
sage: 123.digits(base=2,padto=3) # padto is the minimal length
[1, 1, 0, 1, 1, 1, 1]
sage: 123.digits(base=2,padto=10,digits=(1,-1))
[-1, -1, 1, -1, -1, -1, -1, 1, 1, 1]
sage: a=9939082340; a.digits(10)
[0, 4, 3, 2, 8, 0, 9, 3, 9, 9]
sage: a.digits(512)
[100, 302, 26, 74]
sage: (-12).digits(10)
[-2, -1]
sage: (-12).digits(2)
[0, 0, -1, -1]
We support large bases.
sage: n=2^6000
sage: n.digits(2^3000)
[0, 0, 1]
sage: base=3; n=25
sage: l=n.digits(base)
sage: # the next relationship should hold for all n,base
sage: sum(base^i*l[i] for i in range(len(l)))==n
True
sage: base=3; n=-30; l=n.digits(base); sum(base^i*l[i] for i in range(len(l)))==n
True
The inverse of this method – constructing an integer from a list of digits and a base – can be done using the above method or by simply using ZZ() with a base:
sage: x = 123; ZZ(x.digits(), 10)
123
sage: x == ZZ(x.digits(6), 6)
True
sage: x == ZZ(x.digits(25), 25)
True
Using sum() and enumerate() to do the same thing is slightly faster in many cases (and balanced_sum() may be faster yet). Of course it gives the same result:
sage: base = 4
sage: sum(digit * base^i for i, digit in enumerate(x.digits(base))) == ZZ(x.digits(base), base)
True
Note: In some cases it is faster to give a digits collection. This would be particularly true for computing the digits of a series of small numbers. In these cases, the code is careful to allocate as few python objects as reasonably possible.
sage: digits = range(15)
sage: l=[ZZ(i).digits(15,digits) for i in range(100)]
sage: l[16]
[1, 1]
This function is comparable to str for speed.
sage: n=3^100000
sage: n.digits(base=10)[-1] # slightly slower than str
1
sage: n=10^10000
sage: n.digits(base=10)[-1] # slightly faster than str
1
AUTHORS:
Returns the integer self / right when self is divisible by right.
If self is not divisible by right, the return value is undefined, and may not even be close to self/right for multi-word integers.
EXAMPLES:
sage: a = 8; b = 4
sage: a.divide_knowing_divisible_by(b)
2
sage: (100000).divide_knowing_divisible_by(25)
4000
sage: (100000).divide_knowing_divisible_by(26) # close (random)
3846
However, often it’s way off.
sage: a = 2^70; a
1180591620717411303424
sage: a // 11 # floor divide
107326510974310118493
sage: a.divide_knowing_divisible_by(11) # way off and possibly random
43215361478743422388970455040
Return True if self divides n.
EXAMPLES:
sage: Z = IntegerRing()
sage: Z(5).divides(Z(10))
True
sage: Z(0).divides(Z(5))
False
sage: Z(10).divides(Z(5))
False
Returns a list of all positive integer divisors of the integer self.
EXAMPLES:
sage: a = -3; a.divisors()
[1, 3]
sage: a = 6; a.divisors()
[1, 2, 3, 6]
sage: a = 28; a.divisors()
[1, 2, 4, 7, 14, 28]
sage: a = 2^5; a.divisors()
[1, 2, 4, 8, 16, 32]
sage: a = 100; a.divisors()
[1, 2, 4, 5, 10, 20, 25, 50, 100]
sage: a = 1; a.divisors()
[1]
sage: a = 0; a.divisors()
...
ValueError: n must be nonzero
sage: a = 2^3 * 3^2 * 17; a.divisors()
[1, 2, 3, 4, 6, 8, 9, 12, 17, 18, 24, 34, 36, 51, 68, 72, 102, 136, 153, 204, 306, 408, 612, 1224]
sage: a = odd_part(factorial(31))
sage: v = a.divisors(); len(v)
172800
sage: prod(e+1 for p,e in factor(a))
172800
sage: all([t.divides(a) for t in v])
True
Note
If one first computes all the divisors and then sorts it, the sorting step can easily dominate the runtime. Note, however, that (non-negative) multiplication on the left preserves relative order. One can leverage this fact to keep the list in order as one computes it using a process similar to that of the merge sort when adding new elements.
Returns the largest integer  such that
such that
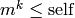 , i.e., the floor of
, i.e., the floor of
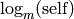 .
.
This is guaranteed to return the correct answer even when the usual log function doesn’t have sufficient precision.
INPUT:
AUTHORS:
David Harvey (2006-09-15)
and/or easy cases up to 100x faster..
EXAMPLES:
sage: Integer(125).exact_log(5)
3
sage: Integer(124).exact_log(5)
2
sage: Integer(126).exact_log(5)
3
sage: Integer(3).exact_log(5)
0
sage: Integer(1).exact_log(5)
0
sage: Integer(178^1700).exact_log(178)
1700
sage: Integer(178^1700-1).exact_log(178)
1699
sage: Integer(178^1700+1).exact_log(178)
1700
sage: # we need to exercise the large base code path too
sage: Integer(1780^1700-1).exact_log(1780)
1699
sage: # The following are very very fast.
sage: # Note that for base m a perfect power of 2, we get the exact log by counting bits.
sage: n=2983579823750185701375109835; m=32
sage: n.exact_log(m)
18
sage: # The next is a favorite of mine. The log2 approximate is exact and immediately provable.
sage: n=90153710570912709517902579010793251709257901270941709247901209742124;m=213509721309572
sage: n.exact_log(m)
4
sage: x = 3^100000
sage: RR(log(RR(x), 3))
100000.000000000
sage: RR(log(RR(x + 100000), 3))
100000.000000000
sage: x.exact_log(3)
100000
sage: (x+1).exact_log(3)
100000
sage: (x-1).exact_log(3)
99999
sage: x.exact_log(2.5)
...
TypeError: Attempt to coerce non-integral RealNumber to Integer
Returns the exponential function of self as a real number.
This function is provided only so that Sage integers may be treated in the same manner as real numbers when convenient.
INPUT:
EXAMPLES:
sage: Integer(8).exp()
e^8
sage: Integer(8).exp(prec=100)
2980.9579870417282747435920995
sage: exp(Integer(8))
e^8
For even fairly large numbers, this may not be useful.
sage: y=Integer(145^145)
sage: y.exp()
e^25024207011349079210459585279553675697932183658421565260323592409432707306554163224876110094014450895759296242775250476115682350821522931225499163750010280453185147546962559031653355159703678703793369785727108337766011928747055351280379806937944746847277089168867282654496776717056860661614337004721164703369140625
sage: y.exp(prec=53) # default RealField precision
+infinity
Return the prime factorization of the integer as a list of pairs
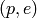 , where
, where  is prime and
is prime and  is a
positive integer.
is a
positive integer.
INPUT:
EXAMPLES:
sage: n = 2^100 - 1; n.factor()
3 * 5^3 * 11 * 31 * 41 * 101 * 251 * 601 * 1801 * 4051 * 8101 * 268501
We use proof=False, which doesn’t prove correctness of the primes that appear in the factorization:
sage: n = 920384092842390423848290348203948092384082349082
sage: n.factor(proof=False)
2 * 11 * 1531 * 4402903 * 10023679 * 619162955472170540533894518173
sage: n.factor(proof=True)
2 * 11 * 1531 * 4402903 * 10023679 * 619162955472170540533894518173
We factor using trial division only:
sage: n.factor(limit=1000)
2 * 11 * 41835640583745019265831379463815822381094652231
Return the factorial 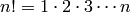 .
Self must fit in an unsigned long int.
.
Self must fit in an unsigned long int.
EXAMPLES:
sage: for n in srange(7):
... print n, n.factorial()
0 1
1 1
2 2
3 6
4 24
5 120
6 720
Return the floor of self, which is just self since self is an integer.
EXAMPLES:
sage: n = 6
sage: n.floor()
6
The gamma function on integers is the factorial function (shifted
by one) on positive integers, and 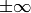 on
non-positive integers.
on
non-positive integers.
EXAMPLES:
sage: gamma(5)
24
sage: gamma(0)
Infinity
sage: gamma(-1)
Infinity
sage: gamma(-2^150)
Infinity
Return the greatest common divisor of self and  .
.
EXAMPLE:
sage: gcd(-1,1)
1
sage: gcd(0,1)
1
sage: gcd(0,0)
0
sage: gcd(2,2^6)
2
sage: gcd(21,2^6)
1
Returns the imaginary part of self, which is zero.
EXAMPLES:
sage: Integer(9).imag()
0
Returns the inverse of self modulo  , if this inverse
exists. Otherwise, raises a ZeroDivisionError
exception.
, if this inverse
exists. Otherwise, raises a ZeroDivisionError
exception.
INPUT:
OUTPUT:
IMPLEMENTATION:
Call the mpz_invert GMP library function.
EXAMPLES:
sage: a = Integer(189)
sage: a.inverse_mod(10000)
4709
sage: a.inverse_mod(-10000)
4709
sage: a.inverse_mod(1890)
...
ZeroDivisionError: Inverse does not exist.
sage: a = Integer(19)**100000
sage: b = a*a
sage: c = a.inverse_mod(b)
...
ZeroDivisionError: Inverse does not exist.
Return inverse of self if self is a unit in the integers, i.e., self is -1 or 1. Otherwise, raise a ZeroDivisionError.
EXAMPLES:
sage: (1).inverse_of_unit()
1
sage: (-1).inverse_of_unit()
-1
sage: 5.inverse_of_unit()
...
ZeroDivisionError: Inverse does not exist.
sage: 0.inverse_of_unit()
...
ZeroDivisionError: Inverse does not exist.
Return True since integers are integral, i.e., satisfy a monic polynomial with integer coefficients.
EXAMPLES:
sage: Integer(3).is_integral()
True
Returns True if self is irreducible, i.e. +/- prime
EXAMPLES:
sage: z = 2^31 - 1
sage: z.is_irreducible()
True
sage: z = 2^31
sage: z.is_irreducible()
False
sage: z = 7
sage: z.is_irreducible()
True
sage: z = -7
sage: z.is_irreducible()
True
Returns True if the integer is  ,
otherwise False.
,
otherwise False.
EXAMPLES:
sage: Integer(1).is_one()
True
sage: Integer(0).is_one()
False
Returns True if self is a perfect power.
EXAMPLES:
sage: z = 8
sage: z.is_perfect_power()
True
sage: 144.is_perfect_power()
True
sage: 10.is_perfect_power()
False
sage: (-8).is_perfect_power()
True
sage: (-4).is_perfect_power()
False
This is a test to make sure we workaround a bug in GMP. (See trac #4612.)
sage: [ -a for a in srange(100) if not (-a^3).is_perfect_power() ]
[]
Returns True if self is a perfect power, ie if
there exist integers a and b, 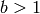 with
with
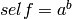 .
.
EXAMPLES:
sage: Integer(-27).is_power()
True
sage: Integer(12).is_power()
False
Returns True if there is an integer b with
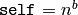 .
.
EXAMPLES:
sage: Integer(64).is_power_of(4)
True
sage: Integer(64).is_power_of(16)
False
TESTS:
sage: Integer(-64).is_power_of(-4)
True
sage: Integer(-32).is_power_of(-2)
True
sage: Integer(1).is_power_of(1)
True
sage: Integer(-1).is_power_of(-1)
True
sage: Integer(0).is_power_of(1)
False
sage: Integer(0).is_power_of(0)
True
sage: Integer(1).is_power_of(0)
True
sage: Integer(1).is_power_of(8)
True
sage: Integer(-8).is_power_of(2)
False
Note
For large integers self, is_power_of() is faster than is_power(). The following examples gives some indication of how much faster.
sage: b = lcm(range(1,10000))
sage: b.exact_log(2)
14446
sage: t=cputime()
sage: for a in range(2, 1000): k = b.is_power()
sage: cputime(t) # random
0.53203299999999976
sage: t=cputime()
sage: for a in range(2, 1000): k = b.is_power_of(2)
sage: cputime(t) # random
0.0
sage: t=cputime()
sage: for a in range(2, 1000): k = b.is_power_of(3)
sage: cputime(t) # random
0.032002000000000308
sage: b = lcm(range(1, 1000))
sage: b.exact_log(2)
1437
sage: t=cputime()
sage: for a in range(2, 10000): k = b.is_power() # note that we change the range from the example above
sage: cputime(t) # random
0.17201100000000036
sage: t=cputime(); TWO=int(2)
sage: for a in range(2, 10000): k = b.is_power_of(TWO)
sage: cputime(t) # random
0.0040000000000000036
sage: t=cputime()
sage: for a in range(2, 10000): k = b.is_power_of(3)
sage: cputime(t) # random
0.040003000000000011
sage: t=cputime()
sage: for a in range(2, 10000): k = b.is_power_of(a)
sage: cputime(t) # random
0.02800199999999986
Returns True if self is prime.
Note
Integer primes are by definition positive! This is different than Magma, but the same as in Pari. See also the is_irreducible() method.
EXAMPLES:
sage: z = 2^31 - 1
sage: z.is_prime()
True
sage: z = 2^31
sage: z.is_prime()
False
sage: z = 7
sage: z.is_prime()
True
sage: z = -7
sage: z.is_prime()
False
sage: z.is_irreducible()
True
IMPLEMENTATION: Calls the PARI isprime function.
Returns True if  is a prime power, and False otherwise.
is a prime power, and False otherwise.
INPUT:
EXAMPLES:
sage: (-10).is_prime_power()
False
sage: (10).is_prime_power()
False
sage: (64).is_prime_power()
True
sage: (3^10000).is_prime_power()
True
sage: (10000).is_prime_power(flag=1)
False
Note
Currently in the case when self is a perfect power, we call self.factor, due to a bug in Pari’s ispower function. See Trac #4777. We illustrate that this is fixed below.
sage: n = 150607571^14
sage: n.is_prime_power()
True
Returns True if self is a pseudoprime
EXAMPLES:
sage: z = 2^31 - 1
sage: z.is_pseudoprime()
True
sage: z = 2^31
sage: z.is_pseudoprime()
False
Returns True if self is a perfect square
EXAMPLES:
sage: Integer(4).is_square()
True
sage: Integer(41).is_square()
False
Returns True if this integer is not divisible by the square of any prime and False otherwise.
EXAMPLES:
sage: Integer(100).is_squarefree()
False
sage: Integer(102).is_squarefree()
True
Returns true if this integer is a unit, i.e., 1 or
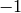 .
.
EXAMPLES:
sage: for n in srange(-2,3):
... print n, n.is_unit()
-2 False
-1 True
0 False
1 True
2 False
Returns the integer floor of the square root of self, or raises an ValueError if self is negative.
EXAMPLE:
sage: a = Integer(5)
sage: a.isqrt()
2
sage: Integer(-102).isqrt()
...
ValueError: square root of negative integer not defined.
Calculate the Jacobi symbol 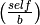 .
.
EXAMPLES:
sage: z = -1
sage: z.jacobi(17)
1
sage: z.jacobi(19)
-1
sage: z.jacobi(17*19)
-1
sage: (2).jacobi(17)
1
sage: (3).jacobi(19)
-1
sage: (6).jacobi(17*19)
-1
sage: (6).jacobi(33)
0
sage: a = 3; b = 7
sage: a.jacobi(b) == -b.jacobi(a)
True
Calculate the Kronecker symbol
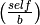 with the Kronecker extension
with the Kronecker extension
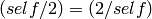 when self odd, or
when self odd, or 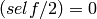 when
when 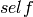 even.
even.
EXAMPLES:
sage: z = 5
sage: z.kronecker(41)
1
sage: z.kronecker(43)
-1
sage: z.kronecker(8)
-1
sage: z.kronecker(15)
0
sage: a = 2; b = 5
sage: a.kronecker(b) == b.kronecker(a)
True
Return a list with this integer in it, to be compatible with the method for number fields.
EXAMPLES:
sage: m = 5
sage: m.list()
[5]
Returns symbolic log by default, unless the logarithm is exact (for an integer base). When precision is given, the RealField approximation to that bit precision is used.
This function is provided primarily so that Sage integers may be treated in the same manner as real numbers when convenient. Direct use of exact_log is probably best for arithmetic log computation.
INPUT:
EXAMPLES:
sage: Integer(124).log(5)
log(124)/log(5)
sage: Integer(124).log(5,100)
2.9950093311241087454822446806
sage: Integer(125).log(5)
3
sage: Integer(125).log(5,prec=53)
3.00000000000000
sage: log(Integer(125))
log(125)
For extremely large numbers, this works:
sage: x = 3^100000
sage: log(x,3)
100000
With the new Pynac symbolic backend, log(x) also works in a reasonable amount of time for this x:
sage: x = 3^100000
sage: log(x)
log(1334971414230...5522000001)
But approximations are probably more useful in this case, and work to as high a precision as we desire:
sage: x.log(3,53) # default precision for RealField
100000.000000000
sage: (x+1).log(3,53)
100000.000000000
sage: (x+1).log(3,1000)
100000.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
We can use non-integer bases, with default e:
sage: x.log(2.5,prec=53)
119897.784671579
We also get logarithms of negative integers, via the
symbolic ring, using the branch from 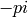 to
to 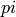 :
:
sage: log(-1)
I*pi
The logarithm of zero is done likewise:
sage: log(0)
-Infinity
Computes the k-th factorial 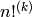 of self. For k=1
this is the standard factorial, and for k greater than one it is
the product of every k-th terms down from self to k. The recursive
definition is used to extend this function to the negative
integers.
of self. For k=1
this is the standard factorial, and for k greater than one it is
the product of every k-th terms down from self to k. The recursive
definition is used to extend this function to the negative
integers.
EXAMPLES:
sage: 5.multifactorial(1)
120
sage: 5.multifactorial(2)
15
sage: 23.multifactorial(2)
316234143225
sage: prod([1..23, step=2])
316234143225
sage: (-29).multifactorial(7)
1/2640
Return the multiplicative order of self.
EXAMPLES:
sage: ZZ(1).multiplicative_order()
1
sage: ZZ(-1).multiplicative_order()
2
sage: ZZ(0).multiplicative_order()
+Infinity
sage: ZZ(2).multiplicative_order()
+Infinity
Return the number of bits in self.
EXAMPLES:
sage: 500.nbits()
9
sage: 5.nbits()
3
sage: 12345.nbits() == len(12345.binary())
True
Return the number of digits of self expressed in the given base.
INPUT:
EXAMPLES:
sage: n = 52
sage: n.ndigits()
2
sage: n = -10003
sage: n.ndigits()
5
sage: n = 15
sage: n.ndigits(2)
4
sage: n=1000**1000000+1
sage: n.ndigits()
3000001
sage: n=1000**1000000-1
sage: n.ndigits()
3000000
sage: n=10**10000000-10**9999990
sage: n.ndigits()
10000000
Returns the next prime after self.
INPUT:
EXAMPLES:
sage: Integer(100).next_prime()
101
Use Proof = False, which is way faster:
sage: b = (2^1024).next_prime(proof=False)
sage: Integer(0).next_prime()
2
sage: Integer(1001).next_prime()
1009
Returns the next probable prime after self, as determined by PARI.
EXAMPLES:
sage: (-37).next_probable_prime()
2
sage: (100).next_probable_prime()
101
sage: (2^512).next_probable_prime()
13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084171
sage: 0.next_probable_prime()
2
sage: 126.next_probable_prime()
127
sage: 144168.next_probable_prime()
144169
Returns the (possibly truncated) n’th root of self.
INPUT:
OUTPUT: If truncate_mode is 0 (default), then returns the exact n’th root if self is an n’th power, or raises a ValueError if it is not.
If truncate_mode is 1, then if either n is odd or self is positive, returns a pair (root, exact_flag) where root is the truncated nth root (rounded towards zero) and exact_flag is a boolean indicating whether the root extraction was exact; otherwise raises a ValueError.
AUTHORS:
EXAMPLES:
sage: Integer(125).nth_root(3)
5
sage: Integer(124).nth_root(3)
...
ValueError: 124 is not a 3rd power
sage: Integer(124).nth_root(3, truncate_mode=1)
(4, False)
sage: Integer(125).nth_root(3, truncate_mode=1)
(5, True)
sage: Integer(126).nth_root(3, truncate_mode=1)
(5, False)
sage: Integer(-125).nth_root(3)
-5
sage: Integer(-125).nth_root(3,truncate_mode=1)
(-5, True)
sage: Integer(-124).nth_root(3,truncate_mode=1)
(-4, False)
sage: Integer(-126).nth_root(3,truncate_mode=1)
(-5, False)
sage: Integer(125).nth_root(2, True)
(11, False)
sage: Integer(125).nth_root(3, True)
(5, True)
sage: Integer(125).nth_root(-5)
...
ValueError: n (=-5) must be positive
sage: Integer(-25).nth_root(2)
...
ValueError: cannot take even root of negative number
sage: a=9
sage: a.nth_root(3)
...
ValueError: 9 is not a 3rd power
sage: a.nth_root(22)
...
ValueError: 9 is not a 22nd power
sage: ZZ(2^20).nth_root(21)
...
ValueError: 1048576 is not a 21st power
sage: ZZ(2^20).nth_root(21, truncate_mode=1)
(1, False)
Return the numerator of this integer.
EXAMPLE:
sage: x = 5
sage: x.numerator()
5
sage: x = 0
sage: x.numerator()
0
Synonym for valuation
EXAMPLES:
sage: n=12
sage: n.ord(3)
1
Returns a string representation of the ordinal associated to self.
EXAMPLES:
sage: [ZZ(n).ordinal_str() for n in range(25)]
['0th',
'1st',
'2nd',
'3rd',
'4th',
...
'10th',
'11th',
'12th',
'13th',
'14th',
...
'20th',
'21st',
'22nd',
'23rd',
'24th']
sage: ZZ(1001).ordinal_str()
'1001st'
sage: ZZ(113).ordinal_str()
'113th'
sage: ZZ(112).ordinal_str()
'112th'
sage: ZZ(111).ordinal_str()
'111th'
Return the number of 1 bits in the binary representation. If self<0, we return Infinity.
EXAMPLES:
sage: n = 123
sage: n.str(2)
'1111011'
sage: n.popcount()
6
sage: n = -17
sage: n.popcount()
+Infinity
Compute self**exp modulo mod.
EXAMPLES:
sage: z = 2
sage: z.powermod(31,31)
2
sage: z.powermod(0,31)
1
sage: z.powermod(-31,31) == 2^-31 % 31
True
As expected, the following is invalid:
sage: z.powermod(31,0)
...
ZeroDivisionError: cannot raise to a power modulo 0
Computes self**exp modulo mod, where exp is an unsigned long integer.
EXAMPLES:
sage: z = 32
sage: z.powermodm_ui(2, 4)
0
sage: z.powermodm_ui(2, 14)
2
sage: z.powermodm_ui(2^32-2, 14)
2
sage: z.powermodm_ui(2^32-1, 14)
... # 32-bit
OverflowError: exp (=4294967295) must be <= 4294967294 # 32-bit
8 # 64-bit
sage: z.powermodm_ui(2^65, 14)
...
OverflowError: exp (=36893488147419103232) must be <= 4294967294 # 32-bit
OverflowError: exp (=36893488147419103232) must be <= 18446744073709551614 # 64-bit
The prime divisors of self, sorted in increasing order. If n is negative, we do not include -1 among the prime divisors, since -1 is not a prime number.
EXAMPLES:
sage: a = 1; a.prime_divisors()
[]
sage: a = 100; a.prime_divisors()
[2, 5]
sage: a = -100; a.prime_divisors()
[2, 5]
sage: a = 2004; a.prime_divisors()
[2, 3, 167]
The prime divisors of self, sorted in increasing order. If n is negative, we do not include -1 among the prime divisors, since -1 is not a prime number.
EXAMPLES:
sage: a = 1; a.prime_divisors()
[]
sage: a = 100; a.prime_divisors()
[2, 5]
sage: a = -100; a.prime_divisors()
[2, 5]
sage: a = 2004; a.prime_divisors()
[2, 3, 167]
Returns the prime-to-m part of self, i.e., the largest divisor of self that is coprime to m.
INPUT:
OUTPUT: Integer
EXAMPLES:
sage: z = 43434
sage: z.prime_to_m_part(20)
21717
Returns the quotient and the remainder of self divided by other. Note that the remainder returned is always either zero or of the same sign as other.
INPUT:
OUTPUT:
EXAMPLES:
sage: z = Integer(231)
sage: z.quo_rem(2)
(115, 1)
sage: z.quo_rem(-2)
(-116, -1)
sage: z.quo_rem(0)
...
ZeroDivisionError: Integer division by zero
sage: a = ZZ.random_element(10**50)
sage: b = ZZ.random_element(10**15)
sage: q, r = a.quo_rem(b)
sage: q*b + r == a
True
sage: 3.quo_rem(ZZ['x'].0)
(0, 3)
Return the product of the prime divisors of self.
If self is 0, returns 1.
EXAMPLES:
sage: Integer(10).radical()
10
sage: Integer(20).radical()
10
sage: Integer(-20).radical()
-10
sage: Integer(0).radical()
1
sage: Integer(36).radical()
6
Return the rational reconstruction of this integer modulo m, i.e., the unique (if it exists) rational number that reduces to self modulo m and whose numerator and denominator is bounded by sqrt(m/2).
EXAMPLES:
sage: (3/7)%100
29
sage: (29).rational_reconstruction(100)
3/7
Returns the real part of self, which is self.
EXAMPLES:
sage: Integer(-4).real()
-4
The square root function.
INPUT:
EXAMPLES:
sage: Integer(144).sqrt()
12
sage: sqrt(Integer(144))
12
sage: Integer(102).sqrt()
sqrt(102)
sage: n = 2
sage: n.sqrt(all=True)
[sqrt(2), -sqrt(2)]
sage: n.sqrt(prec=10)
1.4
sage: n.sqrt(prec=100)
1.4142135623730950488016887242
sage: n.sqrt(prec=100,all=True)
[1.4142135623730950488016887242, -1.4142135623730950488016887242]
sage: n.sqrt(extend=False)
...
ValueError: square root of 2 not an integer
sage: Integer(144).sqrt(all=True)
[12, -12]
sage: Integer(0).sqrt(all=True)
[0]
sage: type(Integer(5).sqrt())
<type 'sage.symbolic.expression.Expression'>
sage: type(Integer(5).sqrt(prec=53))
<type 'sage.rings.real_mpfr.RealNumber'>
sage: type(Integer(-5).sqrt(prec=53))
<type 'sage.rings.complex_number.ComplexNumber'>
EXAMPLES:
sage: 5.sqrt_approx(prec=200)
doctest:1172: DeprecationWarning: This function is deprecated. Use sqrt with a given number of bits of precision instead.
2.2360679774997896964091736687312762354406183596115257242709
sage: 5.sqrt_approx()
2.23606797749979
sage: 4.sqrt_approx()
2
Return (s, r) where s is the integer square root of self and
r is the remainder such that 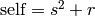 .
Raises ValueError if self is negative.
.
Raises ValueError if self is negative.
EXAMPLES:
sage: 25.sqrtrem()
(5, 0)
sage: 27.sqrtrem()
(5, 2)
sage: 0.sqrtrem()
(0, 0)
sage: Integer(-102).sqrtrem()
...
ValueError: square root of negative integer not defined.
Return the square free part of  (=self), i.e., the
unique integer
(=self), i.e., the
unique integer  that
that 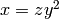 , with
, with
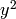 a perfect square and
a perfect square and  square-free.
square-free.
Use self.radical() for the product of the primes that divide self.
If self is 0, just returns 0.
EXAMPLES:
sage: squarefree_part(100)
1
sage: squarefree_part(12)
3
sage: squarefree_part(17*37*37)
17
sage: squarefree_part(-17*32)
-34
sage: squarefree_part(1)
1
sage: squarefree_part(-1)
-1
sage: squarefree_part(-2)
-2
sage: squarefree_part(-4)
-1
sage: a = 8 * 5^6 * 101^2
sage: a.squarefree_part(bound=2).factor()
2 * 5^6 * 101^2
sage: a.squarefree_part(bound=5).factor()
2 * 101^2
sage: a.squarefree_part(bound=1000)
2
sage: a = 7^3 * next_prime(2^100)^2 * next_prime(2^200)
sage: a / a.squarefree_part(bound=1000)
49
Return the string representation of self in the given base.
EXAMPLES:
sage: Integer(2^10).str(2)
'10000000000'
sage: Integer(2^10).str(17)
'394'
sage: two=Integer(2)
sage: two.str(1)
...
ValueError: base (=1) must be between 2 and 36
sage: two.str(37)
...
ValueError: base (=37) must be between 2 and 36
sage: big = 10^5000000
sage: s = big.str() # long time (> 20 seconds)
sage: len(s) # long time (depends on above defn of s)
5000001
sage: s[:10] # long time (depends on above defn of s)
'1000000000'
Return a sorted list of the primes dividing this integer.
OUTPUT: The sorted list of primes appearing in the factorization of this rational with positive exponent.
EXAMPLES:
sage: factorial(10).support()
[2, 3, 5, 7]
sage: (-999).support()
[3, 37]
Trying to find the support of 0 gives an arithmetic error:
sage: 0.support()
...
ArithmeticError: Support of 0 not defined.
Return the bit at index.
EXAMPLES:
sage: w = 6
sage: w.str(2)
'110'
sage: w.test_bit(2)
1
sage: w.test_bit(-1)
0
Return the number of trailing zero bits in self, i.e. the exponent of the largest power of 2 dividing self.
EXAMPLES:
sage: 11.trailing_zero_bits()
0
sage: (-11).trailing_zero_bits()
0
sage: (11<<5).trailing_zero_bits()
5
sage: (-11<<5).trailing_zero_bits()
5
sage: 0.trailing_zero_bits()
0
Returns a pair: the p-adic valuation of self, and the p-adic unit of self.
INPUT:
OUTPUT:
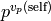
EXAMPLE:
sage: n = 60
sage: n.val_unit(2)
(2, 15)
sage: n.val_unit(3)
(1, 20)
sage: n.val_unit(7)
(0, 60)
sage: (2^11).val_unit(4)
(5, 2)
sage: 0.val_unit(2)
(+Infinity, 1)
Return the p-adic valuation of self.
INPUT:
EXAMPLE:
sage: n = 60
sage: n.valuation(2)
2
sage: n.valuation(3)
1
sage: n.valuation(7)
0
sage: n.valuation(1)
...
ValueError: You can only compute the valuation with respect to a integer larger than 1.
We do not require that p is a prime:
sage: (2^11).valuation(4)
5
Bases: sage.rings.integer.Integer
Rationale for the IntegerWrapper class:
With Integers, the allocation/deallocation function slots are hijacked with custom functions that stick already allocated Integers (with initialized parent and mpz_t fields) into a pool on “deallocation” and then pull them out whenever a new one is needed. Because Integers are so common, this is actually a significant savings. However , this does cause issues with subclassing a Python class directly from Integer (but that’s ok for a Cython class).
As a workaround, one can instead derive a class from the intermediate class IntegerWrapper, which sets statically its alloc/dealloc methods to the original Integer alloc/dealloc methods, before they are swapped manually for the custom ones.
The constructor of IntegerWrapper further allows for specifying an alternative parent to IntegerRing().
Return the LCM of a list v of integers. Elements of v are converted to Sage integers if they aren’t already.
This function is used, e.g., by rings/arith.py
INPUT:
OUTPUT: integer
EXAMPLES:
sage: from sage.rings.integer import LCM_list
sage: w = LCM_list([3,9,30]); w
90
sage: type(w)
<type 'sage.rings.integer.Integer'>
The inputs are converted to Sage integers.
sage: w = LCM_list([int(3), int(9), '30']); w
90
sage: type(w)
<type 'sage.rings.integer.Integer'>
Return true if x is of the Sage integer type.
EXAMPLES:
sage: from sage.rings.integer import is_Integer
sage: is_Integer(2)
True
sage: is_Integer(2/1)
False
sage: is_Integer(int(2))
False
sage: is_Integer(long(2))
False
sage: is_Integer('5')
False
Bases: sage.categories.morphism.Morphism
EXAMPLES:
sage: f = ZZ.coerce_map_from(long); f
Native morphism:
From: Set of Python objects of type 'long'
To: Integer Ring
sage: f(1rL)
1
sage: f(-10000000000000000000001r)
-10000000000000000000001
Create a Sage integer from the base-32 Python string s. This is used in unpickling integers.
EXAMPLES:
sage: from sage.rings.integer import make_integer
sage: make_integer('-29')
-73
sage: make_integer(29)
...
TypeError: expected string or Unicode object, sage.rings.integer.Integer found