Ring $\ZZ$ of Integers¶

The class IntegerRing represents the ring $\ZZ$ of (arbitrary precision) integers. Each integer is an instance of the class Integer, which is defined in a Pyrex extension module that wraps GMP integers (the mpz_t type in GMP).

sage: Z = IntegerRing(); Z
Integer Ring
sage: Z.characteristic()
0
sage: Z.is_field()
False

There is a unique instances of class IntegerRing. To create an Integer, coerce either a Python int, long, or a string. Various other types will also coerce to the integers, when it makes sense.

sage: a = Z(1234); b = Z(5678); print a, b
1234 5678
sage: type(a)
<type 'sage.rings.integer.Integer'>
sage: a + b
6912
sage: Z('94803849083985934859834583945394')
94803849083985934859834583945394

sage.rings.integer_ring.IntegerRing()¶

Return the integer ring

EXAMPLE:

sage: IntegerRing()
Integer Ring
sage: ZZ==IntegerRing()
True

class sage.rings.integer_ring.IntegerRing_class¶

Bases: sage.rings.ring.PrincipalIdealDomain

The ring of integers.

In order to introduce the ring $\ZZ$ of integers, we illustrate creation, calling a few functions, and working with its elements.

sage: Z = IntegerRing(); Z
Integer Ring
sage: Z.characteristic()
0
sage: Z.is_field()
False
sage: Z.category()
Category of euclidean domains
sage: Z(2^(2^5) + 1)
4294967297

One can give strings to create integers. Strings starting with 0x are interpreted as hexadecimal, and strings starting with 0 are interpreted as octal:

sage: parent('37')
<type 'str'>
sage: parent(Z('37'))
Integer Ring
sage: Z('0x10')
16
sage: Z('0x1a')
26
sage: Z('020')
16

As an inverse to digits(), lists of digits are accepted, provided that you give a base. The lists are interpreted in little-endian order, so that entry i of the list is the coefficient of base^i:

sage: Z([3, 7], 10)
73
sage: Z([3, 7], 9)
66
sage: Z([], 10)
0

We next illustrate basic arithmetic in $\ZZ$ :

sage: a = Z(1234); b = Z(5678); print a, b
1234 5678
sage: type(a)
<type 'sage.rings.integer.Integer'>
sage: a + b
6912
sage: b + a
6912
sage: a * b
7006652
sage: b * a
7006652
sage: a - b
-4444
sage: b - a
4444

When we divide to integers using /, the result is automatically coerced to the field of rational numbers, even if the result is an integer.

sage: a / b
617/2839
sage: type(a/b)
<type 'sage.rings.rational.Rational'>
sage: a/a
1
sage: type(a/a)
<type 'sage.rings.rational.Rational'>

For floor division, instead using the // operator:

sage: a // b
0
sage: type(a//b)
<type 'sage.rings.integer.Integer'>

Next we illustrate arithmetic with automatic coercion. The types that coerce are: str, int, long, Integer.

sage: a + 17
1251
sage: a * 374
461516
sage: 374 * a
461516
sage: a/19
1234/19
sage: 0 + Z(-64)
-64

Integers can be coerced:

sage: a = Z(-64)
sage: int(a)
-64

We can create integers from several types of objects.

sage: ZZ(17/1)
17
sage: ZZ(Mod(19,23))
19
sage: ZZ(2 + 3*5 + O(5^3))
17

absolute_degree()¶

Return the absolute degree of the integers, which is 1

EXAMPLE:

sage: ZZ.absolute_degree()
1

characteristic()¶

Return the characteristic of the integers, which is 0

EXAMPLE:

sage: ZZ.characteristic()
0

completion(p, prec, extras={})¶

Returns the completion of Z at p.

EXAMPLES:

sage: ZZ.completion(infinity, 53)
Real Field with 53 bits of precision
sage: ZZ.completion(5, 15, {'print_mode': 'bars'})
5-adic Ring with capped relative precision 15

degree()¶

Return the degree of the integers, which is 1

EXAMPLE:

sage: ZZ.degree()
1

extension(poly, names=None, embedding=None)¶

Returns the order in the number field defined by poly generated (as a ring) by a root of poly.

EXAMPLES:

sage: ZZ.extension(x^2-5, 'a')
Order in Number Field in a with defining polynomial x^2 - 5
sage: ZZ.extension([x^2 + 1, x^2 + 2], 'a,b')
Relative Order in Number Field in a with defining polynomial x^2 + 1 over its base field

fraction_field()¶

Returns the field of rational numbers - the fraction field of the integers.

EXAMPLES:

sage: ZZ.fraction_field()
Rational Field
sage: ZZ.fraction_field() == QQ
True

gen(n=0)¶

Returns the additive generator of the integers, which is 1.

EXAMPLES:

sage: ZZ.gen()
1
sage: type(ZZ.gen())
<type 'sage.rings.integer.Integer'>

gens()¶

Returns the tuple (1,) containing a single element, the additive generator of the integers, which is 1.

EXAMPLES:

sage: ZZ.gens(); ZZ.gens()[0]
(1,)
1
sage: type(ZZ.gens()[0])
<type 'sage.rings.integer.Integer'>

is_atomic_repr()¶

Return True, since elements of the integers do not have to be printed with parentheses around them, when they are coefficients, e.g., in a polynomial.

EXAMPLE:

sage: ZZ.is_atomic_repr()
True

is_field(proof=True)¶

Return False - the integers are not a field.

EXAMPLES:

sage: ZZ.is_field()
False

is_finite()¶

Return False - the integers are an infinite ring.

EXAMPLES:

sage: ZZ.is_finite()
False

is_integrally_closed()¶

Returns that the integer ring is, in fact, an integrally closed ring.

EXAMPLE:

sage: ZZ.is_integrally_closed()
True

is_noetherian()¶

Return True - the integers are a Noetherian ring.

EXAMPLES:

sage: ZZ.is_noetherian()
True

is_subring(other)¶

Return True if ZZ is a subring of other in a natural way.

Every ring of characteristic 0 contains ZZ as a subring.

EXAMPLES:

sage: ZZ.is_subring(QQ)
True

krull_dimension()¶

Return the Krull dimension of the integers, which is 1.

EXAMPLE:

sage: ZZ.krull_dimension()
1

ngens()¶

Returns the number of additive generators of the ring, which is 1.

EXAMPLES:

sage: ZZ.ngens()
1
sage: len(ZZ.gens())
1

order()¶

Return the order (cardinality) of the integers, which is +Infinity.

EXAMPLE:

sage: ZZ.order()
+Infinity

parameter()¶

Returns an integer of degree 1 for the Euclidean property of ZZ, namely 1.

EXAMPLES:

sage: ZZ.parameter()
1

quotient(I, names=None)¶

Return the quotient of $\ZZ$ by the ideal $I$ or integer $I$ .

EXAMPLES:

sage: ZZ.quo(6*ZZ)
Ring of integers modulo 6
sage: ZZ.quo(0*ZZ)
Integer Ring
sage: ZZ.quo(3)
Ring of integers modulo 3
sage: ZZ.quo(3*QQ)
...
TypeError: I must be an ideal of ZZ

random_element(x=None, y=None, distribution=None)¶

Return a random integer.

ZZ.random_element()

return an integer using the default distribution described below

ZZ.random_element(n)

return an integer uniformly distributed between 0 and n-1, inclusive.

ZZ.random_element(min, max)

return an integer uniformly distributed between min and max-1, inclusive.

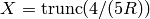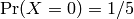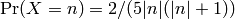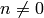The default distribution for ZZ.random_element() is based on $X = \mbox{trunc}(4/(5R))$ , where $R$ is a random variable uniformly distributed between -1 and 1. This gives $\mbox{Pr}(X = 0) = 1/5$ , and $\mbox{Pr}(X = n) = 2/(5|n|(|n|+1))$ for $n \neq 0$ . Most of the samples will be small; -1, 0, and 1 occur with probability 1/5 each. 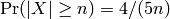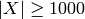But we also have a small but non-negligible proportion of “outliers”; $\mbox{Pr}(|X| \geq n) = 4/(5n)$ , so for instance, we expect that $|X| \geq 1000$ on one in 1250 samples.

We actually use an easy-to-compute truncation of the above distribution; the probabilities given above hold fairly well up to about 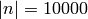$|n| = 10000$ , but around 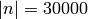$|n| = 30000$ some values will never be returned at all, and we will never return anything greater than $2^{30}$ .

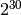EXAMPLES:

The default distribution is on average 50% 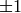$\pm 1$

sage: [ZZ.random_element() for _ in range(10)]
[-8, 2, 0, 0, 1, -1, 2, 1, -95, -1]

The default uniform distribution is integers between -2 and 2 inclusive:

sage: [ZZ.random_element(distribution="uniform") \
        for _ in range(10)]
[2, -2, 2, -2, -1, 1, -1, 2, 1, 0]

If a range is given, the distribution is uniform in that range:

sage: ZZ.random_element(-10,10)
-5
sage: ZZ.random_element(10)
7
sage: ZZ.random_element(10^50)
62498971546782665598023036522931234266801185891699
sage: [ZZ.random_element(5) for _ in range(10)]
[1, 3, 4, 0, 3, 4, 0, 3, 0, 1]

Notice that the right endpoint is not included:

sage: [ZZ.random_element(-2,2) for _ in range(10)]
[-1, -2, 0, -2, 1, -1, -1, -2, -2, 1]

We compute a histogram over 1000 samples of the default distribution:

sage: from collections import defaultdict
sage: d = defaultdict(lambda: 0)
sage: for _ in range(1000): 
...       samp = ZZ.random_element()
...       d[samp] = d[samp] + 1
sage: sorted(d.items())
[(-1026, 1), (-248, 1), (-145, 1), (-81, 1), (-80, 1), (-79, 1), (-75, 1), (-69, 1), (-68, 1), (-63, 2), (-61, 1), (-57, 1), (-50, 1), (-37, 1), (-35, 1), (-33, 1), (-29, 2), (-27, 2), (-25, 1), (-23, 2), (-22, 2), (-20, 1), (-19, 1), (-18, 1), (-16, 4), (-15, 3), (-14, 1), (-13, 2), (-12, 2), (-11, 2), (-10, 7), (-9, 3), (-8, 3), (-7, 7), (-6, 8), (-5, 13), (-4, 24), (-3, 34), (-2, 75), (-1, 207), (0, 209), (1, 189), (2, 64), (3, 35), (4, 13), (5, 11), (6, 10), (7, 4), (8, 4), (10, 1), (11, 1), (12, 1), (13, 1), (14, 1), (16, 3), (18, 1), (19, 1), (26, 2), (27, 1), (28, 1), (29, 1), (30, 1), (32, 1), (33, 2), (35, 1), (37, 1), (39, 1), (41, 1), (42, 1), (52, 1), (91, 1), (94, 1), (106, 1), (111, 1), (113, 2), (132, 1), (134, 1), (232, 1), (240, 1), (2133, 1), (3636, 1)]

range(start, end=None, step=None)¶

Optimized range function for Sage integer.

AUTHORS:

Robert Bradshaw (2007-09-20)

EXAMPLES:

sage: ZZ.range(10)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
sage: ZZ.range(-5,5)
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4]
sage: ZZ.range(0,50,5)
[0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
sage: ZZ.range(0,50,-5)
[]
sage: ZZ.range(50,0,-5)
[50, 45, 40, 35, 30, 25, 20, 15, 10, 5]
sage: ZZ.range(50,0,5)
[]
sage: ZZ.range(50,-1,-5)
[50, 45, 40, 35, 30, 25, 20, 15, 10, 5, 0]

It uses different code if the step doesn’t fit in a long:

sage: ZZ.range(0,2^83,2^80)
[0, 1208925819614629174706176, 2417851639229258349412352, 3626777458843887524118528, 4835703278458516698824704, 6044629098073145873530880, 7253554917687775048237056, 8462480737302404222943232]

Make sure #8818 is fixed:

sage: ZZ.range(1r, 10r)
[1, 2, 3, 4, 5, 6, 7, 8, 9]

residue_field(prime, check=True)¶

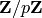Return the residue field of the integers modulo the given prime, ie $\ZZ/p\ZZ$ .

INPUT:

prime - a prime number
check - (boolean, default True) whether or not to check the primality of prime.

OUTPUT: The residue field at this prime.

EXAMPLES:

sage: F = ZZ.residue_field(61); F
Residue field of Integers modulo 61
sage: pi = F.reduction_map(); pi
Partially defined reduction map from Rational Field to Residue field of Integers modulo 61
sage: pi(123/234)
6
sage: pi(1/61)
...
ZeroDivisionError: Cannot reduce rational 1/61 modulo 61: it has negative valuation
sage: lift = F.lift_map(); lift
Lifting map from Residue field of Integers modulo 61 to Rational Field
sage: lift(F(12345/67890))
33
sage: (12345/67890) % 61
33

Construction can be from a prime ideal instead of a prime:

sage: ZZ.residue_field(ZZ.ideal(97))
Residue field of Integers modulo 97

TESTS:

sage: ZZ.residue_field(ZZ.ideal(96))
...
TypeError: Principal ideal (96) of Integer Ring is not prime
sage: ZZ.residue_field(96)
...
TypeError: 96 is not prime

zeta(n=2)¶

Return a primitive n’th root of unity in the integers, or raise an error if none exists

INPUT:

n - a positive integer (default 2)

OUTPUT: an n’th root of unity in ZZ

EXAMPLE:

sage: ZZ.zeta()
-1
sage: ZZ.zeta(1)
1
sage: ZZ.zeta(3)
...
ValueError: no nth root of unity in integer ring
sage: ZZ.zeta(0)
...
ValueError: n must be positive in zeta()

sage.rings.integer_ring.clear_mpz_globals()¶

sage.rings.integer_ring.crt_basis(X, xgcd=None)¶

Compute and return a Chinese Remainder Theorem basis for the list X of coprime integers.

INPUT:

X - a list of Integers that are coprime in pairs

OUTPUT:

E - a list of Integers such that E[i] = 1 (mod X[i]) and E[i] = 0 (mod X[j]) for all j!=i.

The E[i] have the property that if A is a list of objects, e.g., integers, vectors, matrices, etc., where A[i] is moduli X[i], then a CRT lift of A is simply

sum E[i] * A[i].

ALGORITHM: To compute E[i], compute integers s and t such that

s * X[i] + t * (prod over i!=j of X[j]) = 1. (*)

Then E[i] = t * (prod over i!=j of X[j]). Notice that equation (*) implies that E[i] is congruent to 1 modulo X[i] and to 0 modulo the other X[j] for j!=i.

COMPLEXITY: We compute len(X) extended GCD’s.

EXAMPLES:

sage: X = [11,20,31,51]
sage: E = crt_basis([11,20,31,51])
sage: E[0]%X[0]; E[1]%X[0]; E[2]%X[0]; E[3]%X[0]
1
0
0
0
sage: E[0]%X[1]; E[1]%X[1]; E[2]%X[1]; E[3]%X[1]
0
1
0
0
sage: E[0]%X[2]; E[1]%X[2]; E[2]%X[2]; E[3]%X[2]
0
0
1
0
sage: E[0]%X[3]; E[1]%X[3]; E[2]%X[3]; E[3]%X[3]
0
0
0
1

sage.rings.integer_ring.factor(n, algorithm='pari', proof=True)¶

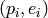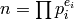Return the factorization of the positive integer $n$ as a sorted list of tuples $(p_i,e_i)$ such that $n=\prod p_i^{e_i}$ .

For further documentation see sage.rings.arith.factor()

EXAMPLE:

sage: sage.rings.integer_ring.factor(420)
2^2 * 3 * 5 * 7

sage.rings.integer_ring.gmp_randrange(n1, n2)¶

sage.rings.integer_ring.init_mpz_globals()¶

sage.rings.integer_ring.is_IntegerRing(x)¶

Internal function: returns true iff x is the ring ZZ of integers

EXAMPLES:

sage: from sage.rings.integer_ring import  is_IntegerRing
sage: is_IntegerRing(ZZ)
True          
sage: is_IntegerRing(QQ)
False
sage: is_IntegerRing(parent(3))
True  
sage: is_IntegerRing(parent(1/3))
False

Ring $\ZZ$ of Integers¶

Previous topic

Next topic

This Page

Navigation

Ring of Integers¶

Previous topic

Next topic

This Page

Quick search

Navigation

Ring $\ZZ$ of Integers¶