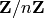 of integers modulo
of integers modulo  ¶
¶EXAMPLES:
sage: R = Integers(97)
sage: a = R(5)
sage: a**100000000000000000000000000000000000000000000000000000000000000
61
This example illustrates the relation between
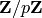 and
and 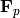 . In
particular, there is a canonical map to
. In
particular, there is a canonical map to 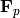 , but not in
the other direction.
, but not in
the other direction.
sage: r = Integers(7)
sage: s = GF(7)
sage: r.has_coerce_map_from(s)
False
sage: s.has_coerce_map_from(r)
True
sage: s(1) + r(1)
2
sage: parent(s(1) + r(1))
Finite Field of size 7
sage: parent(r(1) + s(1))
Finite Field of size 7
We list the elements of 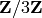
sage: R = Integers(3)
sage: list(R)
[0, 1, 2]
AUTHORS:
Bases: sage.structure.factory.UniqueFactory
Return the quotient ring 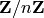 .
.
INPUT:
EXAMPLES:
sage: IntegerModRing(15)
Ring of integers modulo 15
sage: IntegerModRing(7)
Ring of integers modulo 7
sage: IntegerModRing(-100)
Ring of integers modulo 100
Note that you can also use Integers, which is a synonym for IntegerModRing.
sage: Integers(18)
Ring of integers modulo 18
sage: Integers() is Integers(0) is ZZ
True
EXAMPLES:
sage: R = Integers(10)
sage: loads(dumps(R)) is R
True
Bases: sage.rings.quotient_ring.QuotientRing_generic
The ring of integers modulo N, with N composite.
EXAMPLES:
sage: R = IntegerModRing(97)
sage: a = R(5)
sage: a**(10^62)
61
EXAMPLES:
sage: R = IntegerModRing(18)
sage: FF = IntegerModRing(17)
sage: FF.characteristic()
17
sage: R.characteristic()
18
EXAMPLES:
sage: R = Integers(15)
sage: f = R.coerce_map_from(Integers(450)); f
Natural morphism:
From: Ring of integers modulo 450
To: Ring of integers modulo 15
sage: f(-1)
14
sage: f = R.coerce_map_from(int); f
Native morphism:
From: Set of Python objects of type 'int'
To: Ring of integers modulo 15
sage: f(-1r)
14
sage: f = R.coerce_map_from(ZZ); f
Natural morphism:
From: Integer Ring
To: Ring of integers modulo 15
sage: f(-1)
14
sage: f = R.coerce_map_from(Integers(10)); print f
None
sage: f = R.coerce_map_from(QQ); print f
None
Return 1.
EXAMPLE:
sage: R = Integers(12345678900)
sage: R.degree()
1
EXAMPLES:
sage: R = IntegerModRing(18)
sage: FF = IntegerModRing(17)
sage: R.factored_order()
2 * 3^2
sage: FF.factored_order()
17
If this ring is a field, return the corresponding field as a finite field, which may have extra functionality and structure. Otherwise, raise a ValueError.
EXAMPLES:
sage: R = Integers(7); R
Ring of integers modulo 7
sage: R.field()
Finite Field of size 7
sage: R = Integers(9)
sage: R.field()
...
ValueError: self must be a field
Return True precisely if the order is prime.
EXAMPLES:
sage: R = IntegerModRing(18)
sage: R.is_field()
False
sage: FF = IntegerModRing(17)
sage: FF.is_field()
True
Return True since Z/NZ is finite for all positive N.
EXAMPLES:
sage: R = IntegerModRing(18)
sage: R.is_finite()
True
Return True if and only if the order of self is prime.
EXAMPLES:
sage: Integers(389).is_integral_domain()
True
sage: Integers(389^2).is_integral_domain()
False
EXAMPLES:
sage: Integers(8).is_noetherian()
True
Return True if the order is prime.
EXAMPLES:
sage: Zmod(7).is_prime_field()
True
sage: Zmod(8).is_prime_field()
False
EXAMPLES:
sage: Integers(18).krull_dimension()
0
Return the polynomial 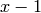 over this ring.
over this ring.
Note
This function exists for consistency with the finite-field modulus function.
EXAMPLES:
sage: R = IntegerModRing(18)
sage: R.modulus()
x + 17
sage: R = IntegerModRing(17)
sage: R.modulus()
x + 16
Return a generator for the multiplicative group of this ring, assuming the multiplicative group is cyclic.
Use the unit_gens function to obtain generators even in the non-cyclic case.
EXAMPLES:
sage: R = Integers(7); R
Ring of integers modulo 7
sage: R.multiplicative_generator()
3
sage: R = Integers(9)
sage: R.multiplicative_generator()
2
sage: Integers(8).multiplicative_generator()
...
ValueError: multiplicative group of this ring is not cyclic
sage: Integers(4).multiplicative_generator()
3
sage: Integers(25*3).multiplicative_generator()
...
ValueError: multiplicative group of this ring is not cyclic
sage: Integers(25*3).unit_gens()
[26, 52]
sage: Integers(162).unit_gens()
[83]
Return True if the multiplicative group of this field is cyclic. This is the case exactly when the order is less than 8, a power of an odd prime, or twice a power of an odd prime.
EXAMPLES:
sage: R = Integers(7); R
Ring of integers modulo 7
sage: R.multiplicative_group_is_cyclic()
True
sage: R = Integers(9)
sage: R.multiplicative_group_is_cyclic()
True
sage: Integers(8).multiplicative_group_is_cyclic()
False
sage: Integers(4).multiplicative_group_is_cyclic()
True
sage: Integers(25*3).multiplicative_group_is_cyclic()
False
We test that #5250 is fixed:
sage: Integers(162).multiplicative_group_is_cyclic()
True
Return generators for each subgroup of
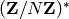 .
.
EXAMPLES:
sage: Integers(5).multiplicative_subgroups()
[[2], [4], []]
sage: Integers(15).multiplicative_subgroups()
[[11, 7], [4, 11], [8], [11], [14], [7], [4], []]
sage: Integers(2).multiplicative_subgroups()
[[]]
sage: len(Integers(341).multiplicative_subgroups())
80
Return a quadratic non-residue in self.
EXAMPLES:
sage: R = Integers(17)
sage: R.quadratic_nonresidue()
3
sage: R(3).is_square()
False
Return a random element of this ring.
If bound is not None, return the coercion of an integer in the interval [-bound, bound] into this ring.
EXAMPLES:
sage: R = IntegerModRing(18)
sage: R.random_element()
2
Return all square roots of 1 in self, i.e., all solutions to
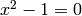 .
.
OUTPUT:
EXAMPLES:
sage: R = Integers(2^10)
sage: [x for x in R if x^2 == 1]
[1, 511, 513, 1023]
sage: R.square_roots_of_one()
(1, 511, 513, 1023)
sage: v = Integers(9*5).square_roots_of_one(); v
(1, 19, 26, 44)
sage: [x^2 for x in v]
[1, 1, 1, 1]
sage: v = Integers(9*5*8).square_roots_of_one(); v
(1, 19, 71, 89, 91, 109, 161, 179, 181, 199, 251, 269, 271, 289, 341, 359)
sage: [x^2 for x in v]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Returns generators for the unit group 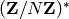 .
.
We compute the list of generators using a deterministic algorithm, so
the generators list will always be the same. For each odd prime divisor
of N there will be exactly one corresponding generator; if N is even
there will be 0, 1 or 2 generators according to whether 2 divides N to
order 1, 2 or 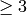 .
.
INPUT: (none)
OUTPUT:
EXAMPLES:
sage: R = IntegerModRing(18)
sage: R.unit_gens()
[11]
sage: R = IntegerModRing(17)
sage: R.unit_gens()
[3]
sage: IntegerModRing(next_prime(10^30)).unit_gens()
[5]
EXAMPLES:
sage: R = IntegerModRing(17)
sage: R.unit_group_exponent()
16
sage: R = IntegerModRing(18)
sage: R.unit_group_exponent()
6
Return the order of the unit group of this residue class ring.
EXAMPLES;
sage: R = Integers(500)
sage: R.unit_group_order()
200
Return True if x is an integer modulo ring.
EXAMPLES:
sage: from sage.rings.finite_rings.integer_mod_ring import is_IntegerModRing
sage: R = IntegerModRing(17)
sage: is_IntegerModRing(R)
True
sage: is_IntegerModRing(GF(13))
True
sage: is_IntegerModRing(GF(4, 'a'))
False
sage: is_IntegerModRing(10)
False
sage: is_IntegerModRing(ZZ)
False