AUTHORS:
TESTS:
sage: R.<x> = PolynomialRing(ZZ)
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: S = R.quotient_ring(I);
sage: S == loads(dumps(S))
True
Creates a quotient ring of the ring  by the ideal
by the ideal  . Variables are
labeled by names (if the quotient ring is a quotient of a
polynomial ring). If names isn’t given, ‘bar’ will be appended to
the variable names in
. Variables are
labeled by names (if the quotient ring is a quotient of a
polynomial ring). If names isn’t given, ‘bar’ will be appended to
the variable names in  .
.
INPUTS:
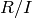
OUTPUTS: 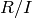 - the quotient ring
- the quotient ring  mod the ideal
mod the ideal 
EXAMPLES:
Some simple quotient rings with the integers:
sage: R = QuotientRing(ZZ,7*ZZ); R
Quotient of Integer Ring by the ideal (7)
sage: R.gens()
(1,)
sage: 1*R(3); 6*R(3); 7*R(3)
3
4
0
sage: S = QuotientRing(ZZ,ZZ.ideal(8)); S
Quotient of Integer Ring by the ideal (8)
sage: 2*S(4)
0
With polynomial rings: (note that the variable name of the quotient ring can be specified as shown below)
sage: R.<xx> = QuotientRing(QQ[x], QQ[x].ideal(x^2 + 1)); R
Univariate Quotient Polynomial Ring in xx over Rational Field with modulus x^2 + 1
sage: R.gens(); R.gen()
(xx,)
xx
sage: for n in range(4): xx^n
1
xx
-1
-xx
sage: S = QuotientRing(QQ[x], QQ[x].ideal(x^2 - 2)); S
Univariate Quotient Polynomial Ring in xbar over Rational Field with
modulus x^2 - 2
sage: xbar = S.gen(); S.gen()
xbar
sage: for n in range(3): xbar^n
1
xbar
2
Sage coerces objects into ideals when possible:
sage: R = QuotientRing(QQ[x], x^2 + 1); R
Univariate Quotient Polynomial Ring in xbar over Rational Field with
modulus x^2 + 1
By Noether’s homomorphism theorems, the quotient of a quotient ring
of  is just the quotient of
is just the quotient of  by the sum of the ideals. In this
example, we end up modding out the ideal
by the sum of the ideals. In this
example, we end up modding out the ideal 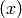 from the ring
from the ring
![\QQ[x,y]](../../_images/math/2521f04fde015efd885c0edf129862daab03e777.png) :
:
sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = QuotientRing(R,R.ideal(1 + y^2))
sage: T.<c,d> = QuotientRing(S,S.ideal(a))
sage: T
Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x, y^2 + 1)
sage: R.gens(); S.gens(); T.gens()
(x, y)
(a, b)
(0, d)
sage: for n in range(4): d^n
1
d
-1
-d
Bases: sage.rings.ring.CommutativeRing, sage.structure.parent_gens.ParentWithGens
The quotient ring of  by the ideal
by the ideal  .
.
EXAMPLES:
sage: R.<x> = PolynomialRing(ZZ,'x')
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: S = R.quotient_ring(I); S
Quotient of Univariate Polynomial Ring in x over Integer Ring by the ideal (x^2 + 3*x + 4, x^2 + 1)
sage: R.<x,y> = PolynomialRing(QQ)
sage: S.<a,b> = R.quo(x^2 + y^2)
sage: a^2 + b^2 == 0
True
sage: S(0) == a^2 + b^2
True
EXAMPLE: Quotient of quotient
A quotient of a quotient is just the quotient of the original top ring by the sum of two ideals.
sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = R.quo(1 + y^2)
sage: T.<c,d> = S.quo(a)
sage: T
Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x, y^2 + 1)
sage: T.gens()
(0, d)
Return the characteristic of the quotient ring.
TODO: Not yet implemented!
EXAMPLES:
sage: Q = QuotientRing(ZZ,7*ZZ)
sage: Q.characteristic()
...
NotImplementedError
EXAMPLES:
sage: R.<x> = PolynomialRing(ZZ,'x')
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: R.quotient_ring(I).construction()
(QuotientFunctor, Univariate Polynomial Ring in x over Integer Ring)
TESTS:
sage: F, R = Integers(5).construction()
sage: F(R)
Ring of integers modulo 5
sage: F, R = GF(5).construction()
sage: F(R)
Finite Field of size 5
The covering ring homomorphism 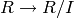 , equipped with a
section.
, equipped with a
section.
EXAMPLES:
sage: R = ZZ.quo(3*ZZ)
sage: pi = R.cover()
sage: pi
Ring morphism:
From: Integer Ring
To: Ring of integers modulo 3
Defn: Natural quotient map
sage: pi(5)
2
sage: l = pi.lift()
EXAMPLES:
sage: R.<x,y> = PolynomialRing(QQ)
sage: Q = R.quo( (x^2,y^2) )
sage: pi = Q.cover()
sage: pi(x^3+y)
ybar
sage: l = pi.lift(x+y^3)
sage: l
x
sage: l = pi.lift(); l
Set-theoretic ring morphism:
From: Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2, y^2)
To: Multivariate Polynomial Ring in x, y over Rational Field
Defn: Choice of lifting map
sage: l(x+y^3)
x
Returns the cover ring of the quotient ring: that is, the original
ring  from which we modded out an ideal,
from which we modded out an ideal,  .
.
EXAMPLES:
sage: Q = QuotientRing(ZZ,7*ZZ)
sage: Q.cover_ring()
Integer Ring
sage: Q = QuotientRing(QQ[x], x^2 + 1)
sage: Q.cover_ring()
Univariate Polynomial Ring in x over Rational Field
Returns the ideal generating this quotient ring.
EXAMPLES:
In the integers:
sage: Q = QuotientRing(ZZ,7*ZZ)
sage: Q.defining_ideal()
Principal ideal (7) of Integer Ring
An example involving a quotient of a quotient. By Noether’s homomorphism theorems, this is actually a quotient by a sum of two ideals:
sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = QuotientRing(R,R.ideal(1 + y^2))
sage: T.<c,d> = QuotientRing(S,S.ideal(a))
sage: S.defining_ideal()
Ideal (y^2 + 1) of Multivariate Polynomial Ring in x, y over Rational Field
sage: T.defining_ideal()
Ideal (x, y^2 + 1) of Multivariate Polynomial Ring in x, y over Rational Field
Returns the  -th generator for this quotient ring.
-th generator for this quotient ring.
EXAMPLES:
sage: R = QuotientRing(ZZ,7*ZZ)
sage: R.gen(0)
1
sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = QuotientRing(R,R.ideal(1 + y^2))
sage: T.<c,d> = QuotientRing(S,S.ideal(a))
sage: T
Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x, y^2 + 1)
sage: R.gen(0); R.gen(1)
x
y
sage: S.gen(0); S.gen(1)
a
b
sage: T.gen(0); T.gen(1)
0
d
Return the ideal of self with the given generators.
EXAMPLES:
sage: R.<x,y> = PolynomialRing(QQ)
sage: S = R.quotient_ring(x^2+y^2)
sage: S.ideal()
Ideal (0) of Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2 + y^2)
sage: S.ideal(x+y+1)
Ideal (xbar + ybar + 1) of Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2 + y^2)
TESTS:
We create an ideal of a fairly generic integer ring (see trac 5666):
sage: R = Integers(10)
sage: R.ideal(1)
Principal ideal (1) of Ring of integers modulo 10
Returns True if the quotient ring is a field. Checks to see if the defining ideal is maximal.
TESTS:
Requires the is_maximal function to be implemented:
sage: Q = QuotientRing(ZZ,7*ZZ)
sage: Q.is_field()
...
NotImplementedError
If this function returns True then self is definitely an integral domain. If it returns False, then either self is definitely not an integral domain or this function was unable to determine whether or not self is an integral domain.
Use self.defining_ideal().is_prime() to find out for sure whether this quotient ring is really not an integral domain, of if Sage is unable to determine the answer.
EXAMPLES:
sage: R = Integers(8)
sage: R.is_integral_domain()
False
sage: R.<a,b,c> = ZZ['a','b','c']
sage: I = R.ideal(a,b)
sage: Q = R.quotient_ring(I)
sage: Q.is_integral_domain()
...
NotImplementedError
Return True if this ring is Noetherian.
EXAMPLES:
sage: R = QuotientRing(ZZ, 102*ZZ)
sage: R.is_noetherian()
True
sage: R = QuotientRing(QQ[x], x^2+1)
sage: R.is_noetherian()
True
If the cover ring of self is not Noetherian, we currently have no way of testing whether self is Noetherian, so we raise an error:
sage: R.<x> = InfinitePolynomialRing(QQ)
sage: R.is_noetherian()
False
sage: I = R.ideal([x[1]^2, x[2]])
sage: S = R.quotient(I)
sage: S.is_noetherian()
...
NotImplementedError
Return the lifting map to the cover.
EXAMPLES:
sage: R.<x,y> = PolynomialRing(QQ, 2)
sage: S = R.quotient(x^2 + y^2)
sage: pi = S.cover(); pi
Ring morphism:
From: Multivariate Polynomial Ring in x, y over Rational Field
To: Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2 + y^2)
Defn: Natural quotient map
sage: L = S.lift(); L
Set-theoretic ring morphism:
From: Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x^2 + y^2)
To: Multivariate Polynomial Ring in x, y over Rational Field
Defn: Choice of lifting map
sage: L(S.0)
x
sage: L(S.1)
y
Note that some reduction may be applied so that the lift of a reduction need not equal the original element.
sage: z = pi(x^3 + 2*y^2); z
-xbar*ybar^2 + 2*ybar^2
sage: L(z)
-x*y^2 + 2*y^2
sage: L(z) == x^3 + 2*y^2
False
Returns the number of generators for this quotient ring.
TODO: Note that ngens counts 0 as a generator. Does this make sense? That is, since 0 only generates itself and the fact that this is true for all rings, is there a way to “knock it off” of the generators list if a generator of some original ring is modded out?
EXAMPLES:
sage: R = QuotientRing(ZZ,7*ZZ)
sage: R.gens(); R.ngens()
(1,)
1
sage: R.<x,y> = PolynomialRing(QQ,2)
sage: S.<a,b> = QuotientRing(R,R.ideal(1 + y^2))
sage: T.<c,d> = QuotientRing(S,S.ideal(a))
sage: T
Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x, y^2 + 1)
sage: R.gens(); S.gens(); T.gens()
(x, y)
(a, b)
(0, d)
sage: R.ngens(); S.ngens(); T.ngens()
2
2
2
Return the term order of this ring.
EXAMPLE:
sage: P.<a,b,c> = PolynomialRing(QQ)
sage: I = Ideal([a^2 - a, b^2 - b, c^2 - c])
sage: Q = P.quotient(I)
sage: Q.term_order()
Degree reverse lexicographic term order
Tests whether or not x inherits from QuotientRing_generic.
EXAMPLES:
sage: from sage.rings.quotient_ring import is_QuotientRing
sage: R.<x> = PolynomialRing(ZZ,'x')
sage: I = R.ideal([4 + 3*x + x^2, 1 + x^2])
sage: S = R.quotient_ring(I)
sage: is_QuotientRing(S)
True
sage: is_QuotientRing(R)
False