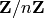 ¶
¶An element of the integers modulo  .
.
There are three types of integer_mod classes, depending on the size of the modulus.
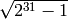 .
.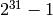 .
.All extend IntegerMod_abstract.
For efficiency reasons, it stores the modulus (in all three forms, if possible) in a common (cdef) class NativeIntStruct rather than in the parent.
AUTHORS:
TESTS:
sage: R = Integers(101^3)
sage: a = R(824362); b = R(205942)
sage: a * b
851127
Bases: sage.rings.finite_rings.integer_mod.IntegerMod_hom
EXAMPLES:
We make sure it works for every type.
sage: from sage.rings.finite_rings.integer_mod import Int_to_IntegerMod
sage: Rs = [Integers(2**k) for k in range(1,50,10)]
sage: [type(R(0)) for R in Rs]
[<type 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_int64'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_gmp'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_gmp'>]
sage: fs = [Int_to_IntegerMod(R) for R in Rs]
sage: [f(-1) for f in fs]
[1, 2047, 2097151, 2147483647, 2199023255551]
Create an integer modulo  with the given parent.
with the given parent.
This is mainly for internal use.
Bases: sage.structure.element.CommutativeRingElement
Returns the additive order of self.
This is the same as self.order().
EXAMPLES:
sage: Integers(20)(2).additive_order()
10
sage: Integers(20)(7).additive_order()
20
sage: Integers(90308402384902)(2).additive_order()
45154201192451
Returns the characteristic polynomial of this element.
EXAMPLES:
sage: k = GF(3)
sage: a = k.gen()
sage: a.charpoly('x')
x + 2
sage: a + 2
0
AUTHORS:
Use the Chinese Remainder Theorem to find an element of the integers modulo the product of the moduli that reduces to self and to other. The modulus of other must be coprime to the modulus of self.
EXAMPLES:
sage: a = mod(3,5)
sage: b = mod(2,7)
sage: a.crt(b)
23
sage: a = mod(37,10^8)
sage: b = mod(9,3^8)
sage: a.crt(b)
125900000037
sage: b = mod(0,1)
sage: a.crt(b) == a
True
sage: a.crt(b).modulus()
100000000
AUTHORS:
Return True if self is nilpotent, i.e., some power of self is zero.
EXAMPLES:
sage: a = Integers(90384098234^3)
sage: factor(a.order())
2^3 * 191^3 * 236607587^3
sage: b = a(2*191)
sage: b.is_nilpotent()
False
sage: b = a(2*191*236607587)
sage: b.is_nilpotent()
True
ALGORITHM: Let 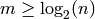 , where
, where  is
the modulus. Then
is
the modulus. Then 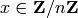 is
nilpotent if and only if
is
nilpotent if and only if 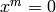 .
.
PROOF: This is clear if you reduce to the prime power case, which you can do via the Chinese Remainder Theorem.
We could alternatively factor  and check to see if the
prime divisors of
and check to see if the
prime divisors of  all divide
all divide  . This is
asymptotically slower :-).
. This is
asymptotically slower :-).
EXAMPLES:
sage: Mod(3,17).is_square()
False
sage: Mod(9,17).is_square()
True
sage: Mod(9,17*19^2).is_square()
True
sage: Mod(-1,17^30).is_square()
True
sage: Mod(1/9, next_prime(2^40)).is_square()
True
sage: Mod(1/25, next_prime(2^90)).is_square()
True
TESTS:
sage: Mod(1/25, 2^8).is_square()
True
sage: Mod(1/25, 2^40).is_square()
True
ALGORITHM: Calculate the Jacobi symbol
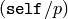 at each prime
at each prime  dividing
dividing  . It must be 1 or 0 for each prime, and if it
is 0 mod
. It must be 1 or 0 for each prime, and if it
is 0 mod  , where
, where 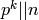 , then
, then
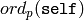 must be even or greater than
must be even or greater than
 .
.
The case 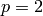 is handled separately.
is handled separately.
AUTHORS:
Return an integer  such that
such that 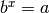 , where
, where
 is self.
is self.
INPUT:

 . If b is not given,
R.multiplicative_generator() is used, where
R is the parent of self.
. If b is not given,
R.multiplicative_generator() is used, where
R is the parent of self.OUTPUT: Integer  such that
such that 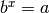 .
.
Note
The base must not be too big or the current implementation, which is in PARI, will fail.
EXAMPLES:
sage: r = Integers(125)
sage: b = r.multiplicative_generator()^3
sage: a = b^17
sage: a.log(b)
17
sage: a.log()
63
A bigger example.
sage: FF = FiniteField(2^32+61)
sage: c = FF(4294967356)
sage: x = FF(2)
sage: a = c.log(x)
sage: a
2147483678
sage: x^a
4294967356
Things that can go wrong. E.g., if the base is not a generator for the multiplicative group, or not even a unit. You can also use the generic function discrete_log.
sage: a = Mod(9, 100); b = Mod(3,100)
sage: a.log(b)
...
ValueError: base (=3) for discrete log must generate multiplicative group
sage: sage.groups.generic.discrete_log(b^2,b)
2
sage: a = Mod(16, 100); b = Mod(4,100)
sage: a.log(b)
...
ValueError: (8)
PARI failed to compute discrete log (perhaps base is not a generator or is too large)
sage: sage.groups.generic.discrete_log(a,b)
...
ZeroDivisionError: Inverse does not exist.
AUTHORS:
Returns the minimal polynomial of this element.
Returns the minimal polynomial of this element.
EXAMPLES:
sage: Mod(3,17).modulus()
17
Returns the multiplicative order of self.
EXAMPLES:
sage: Mod(-1,5).multiplicative_order()
2
sage: Mod(1,5).multiplicative_order()
1
sage: Mod(0,5).multiplicative_order()
...
ArithmeticError: multiplicative order of 0 not defined since it is not a unit modulo 5
Returns the norm of this element, which is itself. (This is here for compatibility with higher order finite fields.)
EXAMPLES:
sage: k = GF(691)
sage: a = k(389)
sage: a.norm()
389
AUTHORS:
Returns an  th root of self.
th root of self.
INPUT:
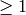 (must fit in C
int type)
(must fit in C
int type) th roots of
self, instead of just one.
th roots of
self, instead of just one.OUTPUT: If self has an  th root, returns one (if
all is false) or a list of all of them (if
all is true). Otherwise, raises a
ValueError.
th root, returns one (if
all is false) or a list of all of them (if
all is true). Otherwise, raises a
ValueError.
AUTHORS:
EXAMPLES:
sage: k.<a> = GF(29)
sage: b = a^2 + 5*a + 1
sage: b.nth_root(5)
24
sage: b.nth_root(7)
...
ValueError: no nth root
sage: b.nth_root(4, all=True)
[21, 20, 9, 8]
Returns a constant polynomial representing this value.
EXAMPLES:
sage: k = GF(7)
sage: a = k.gen(); a
1
sage: a.polynomial()
1
sage: type(a.polynomial())
<type 'sage.rings.polynomial.polynomial_zmod_flint.Polynomial_zmod_flint'>
EXAMPLES:
sage: R = IntegerModRing(97)
sage: a = R(2) / R(3)
sage: a
33
sage: a.rational_reconstruction()
2/3
Returns square root or square roots of self modulo
 .
.
INPUT:
ALGORITHM: Calculates the square roots mod  for each of
the primes
for each of
the primes  dividing the order of the ring, then lifts
them
dividing the order of the ring, then lifts
them  -adically and uses the CRT to find a square root
mod
-adically and uses the CRT to find a square root
mod  .
.
See also square_root_mod_prime_power and square_root_mod_prime (in this module) for more algorithmic details.
EXAMPLES:
sage: mod(-1, 17).sqrt()
4
sage: mod(5, 389).sqrt()
86
sage: mod(7, 18).sqrt()
5
sage: a = mod(14, 5^60).sqrt()
sage: a*a
14
sage: mod(15, 389).sqrt(extend=False)
...
ValueError: self must be a square
sage: Mod(1/9, next_prime(2^40)).sqrt()^(-2)
9
sage: Mod(1/25, next_prime(2^90)).sqrt()^(-2)
25
sage: a = Mod(3,5); a
3
sage: x = Mod(-1, 360)
sage: x.sqrt(extend=False)
...
ValueError: self must be a square
sage: y = x.sqrt(); y
sqrt359
sage: y.parent()
Univariate Quotient Polynomial Ring in sqrt359 over Ring of integers modulo 360 with modulus x^2 + 1
sage: y^2
359
We compute all square roots in several cases:
sage: R = Integers(5*2^3*3^2); R
Ring of integers modulo 360
sage: R(40).sqrt(all=True)
[20, 160, 200, 340]
sage: [x for x in R if x^2 == 40] # Brute force verification
[20, 160, 200, 340]
sage: R(1).sqrt(all=True)
[1, 19, 71, 89, 91, 109, 161, 179, 181, 199, 251, 269, 271, 289, 341, 359]
sage: R(0).sqrt(all=True)
[0, 60, 120, 180, 240, 300]
sage: R = Integers(5*13^3*37); R
Ring of integers modulo 406445
sage: v = R(-1).sqrt(all=True); v
[78853, 111808, 160142, 193097, 213348, 246303, 294637, 327592]
sage: [x^2 for x in v]
[406444, 406444, 406444, 406444, 406444, 406444, 406444, 406444]
sage: v = R(169).sqrt(all=True); min(v), -max(v), len(v)
(13, 13, 104)
sage: all([x^2==169 for x in v])
True
Modulo a power of 2:
sage: R = Integers(2^7); R
Ring of integers modulo 128
sage: a = R(17)
sage: a.sqrt()
23
sage: a.sqrt(all=True)
[23, 41, 87, 105]
sage: [x for x in R if x^2==17]
[23, 41, 87, 105]
Returns square root or square roots of self modulo
 .
.
INPUT:
ALGORITHM: Calculates the square roots mod  for each of
the primes
for each of
the primes  dividing the order of the ring, then lifts
them
dividing the order of the ring, then lifts
them  -adically and uses the CRT to find a square root
mod
-adically and uses the CRT to find a square root
mod  .
.
See also square_root_mod_prime_power and square_root_mod_prime (in this module) for more algorithmic details.
EXAMPLES:
sage: mod(-1, 17).sqrt()
4
sage: mod(5, 389).sqrt()
86
sage: mod(7, 18).sqrt()
5
sage: a = mod(14, 5^60).sqrt()
sage: a*a
14
sage: mod(15, 389).sqrt(extend=False)
...
ValueError: self must be a square
sage: Mod(1/9, next_prime(2^40)).sqrt()^(-2)
9
sage: Mod(1/25, next_prime(2^90)).sqrt()^(-2)
25
sage: a = Mod(3,5); a
3
sage: x = Mod(-1, 360)
sage: x.sqrt(extend=False)
...
ValueError: self must be a square
sage: y = x.sqrt(); y
sqrt359
sage: y.parent()
Univariate Quotient Polynomial Ring in sqrt359 over Ring of integers modulo 360 with modulus x^2 + 1
sage: y^2
359
We compute all square roots in several cases:
sage: R = Integers(5*2^3*3^2); R
Ring of integers modulo 360
sage: R(40).sqrt(all=True)
[20, 160, 200, 340]
sage: [x for x in R if x^2 == 40] # Brute force verification
[20, 160, 200, 340]
sage: R(1).sqrt(all=True)
[1, 19, 71, 89, 91, 109, 161, 179, 181, 199, 251, 269, 271, 289, 341, 359]
sage: R(0).sqrt(all=True)
[0, 60, 120, 180, 240, 300]
sage: R = Integers(5*13^3*37); R
Ring of integers modulo 406445
sage: v = R(-1).sqrt(all=True); v
[78853, 111808, 160142, 193097, 213348, 246303, 294637, 327592]
sage: [x^2 for x in v]
[406444, 406444, 406444, 406444, 406444, 406444, 406444, 406444]
sage: v = R(169).sqrt(all=True); min(v), -max(v), len(v)
(13, 13, 104)
sage: all([x^2==169 for x in v])
True
Modulo a power of 2:
sage: R = Integers(2^7); R
Ring of integers modulo 128
sage: a = R(17)
sage: a.sqrt()
23
sage: a.sqrt(all=True)
[23, 41, 87, 105]
sage: [x for x in R if x^2==17]
[23, 41, 87, 105]
Returns the trace of this element, which is itself. (This is here for compatibility with higher order finite fields.)
EXAMPLES:
sage: k = GF(691)
sage: a = k(389)
sage: a.trace()
389
AUTHORS:
Bases: sage.rings.finite_rings.integer_mod.IntegerMod_abstract
Elements of 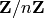 for n not small enough
to be operated on in word size.
for n not small enough
to be operated on in word size.
AUTHORS:
Returns True if this is  , otherwise
False.
, otherwise
False.
EXAMPLES:
sage: mod(1,5^23).is_one()
True
sage: mod(0,5^23).is_one()
False
Return True iff this element is a unit.
EXAMPLES:
sage: mod(13, 5^23).is_unit()
True
sage: mod(25, 5^23).is_unit()
False
Lift an integer modulo  to the integers.
to the integers.
EXAMPLES:
sage: a = Mod(8943, 2^70); type(a)
<type 'sage.rings.finite_rings.integer_mod.IntegerMod_gmp'>
sage: lift(a)
8943
sage: a.lift()
8943
Bases: sage.rings.finite_rings.integer_mod.IntegerMod_abstract
Elements of 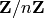 for n small enough to
be operated on in 32 bits
for n small enough to
be operated on in 32 bits
AUTHORS:
Returns True if this is  , otherwise
False.
, otherwise
False.
EXAMPLES:
sage: mod(6,5).is_one()
True
sage: mod(0,5).is_one()
False
Return True iff this element is a unit
EXAMPLES:
sage: a=Mod(23,100)
sage: a.is_unit()
True
sage: a=Mod(24,100)
sage: a.is_unit()
False
Lift an integer modulo  to the integers.
to the integers.
EXAMPLES:
sage: a = Mod(8943, 2^10); type(a)
<type 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>
sage: lift(a)
751
sage: a.lift()
751
Returns square root or square roots of self modulo
 .
.
INPUT:
ALGORITHM: Calculates the square roots mod  for each of
the primes
for each of
the primes  dividing the order of the ring, then lifts
them
dividing the order of the ring, then lifts
them  -adically and uses the CRT to find a square root
mod
-adically and uses the CRT to find a square root
mod  .
.
See also square_root_mod_prime_power and square_root_mod_prime (in this module) for more algorithmic details.
EXAMPLES:
sage: mod(-1, 17).sqrt()
4
sage: mod(5, 389).sqrt()
86
sage: mod(7, 18).sqrt()
5
sage: a = mod(14, 5^60).sqrt()
sage: a*a
14
sage: mod(15, 389).sqrt(extend=False)
...
ValueError: self must be a square
sage: Mod(1/9, next_prime(2^40)).sqrt()^(-2)
9
sage: Mod(1/25, next_prime(2^90)).sqrt()^(-2)
25
sage: a = Mod(3,5); a
3
sage: x = Mod(-1, 360)
sage: x.sqrt(extend=False)
...
ValueError: self must be a square
sage: y = x.sqrt(); y
sqrt359
sage: y.parent()
Univariate Quotient Polynomial Ring in sqrt359 over Ring of integers modulo 360 with modulus x^2 + 1
sage: y^2
359
We compute all square roots in several cases:
sage: R = Integers(5*2^3*3^2); R
Ring of integers modulo 360
sage: R(40).sqrt(all=True)
[20, 160, 200, 340]
sage: [x for x in R if x^2 == 40] # Brute force verification
[20, 160, 200, 340]
sage: R(1).sqrt(all=True)
[1, 19, 71, 89, 91, 109, 161, 179, 181, 199, 251, 269, 271, 289, 341, 359]
sage: R(0).sqrt(all=True)
[0, 60, 120, 180, 240, 300]
sage: GF(107)(0).sqrt(all=True)
[0]
sage: R = Integers(5*13^3*37); R
Ring of integers modulo 406445
sage: v = R(-1).sqrt(all=True); v
[78853, 111808, 160142, 193097, 213348, 246303, 294637, 327592]
sage: [x^2 for x in v]
[406444, 406444, 406444, 406444, 406444, 406444, 406444, 406444]
sage: v = R(169).sqrt(all=True); min(v), -max(v), len(v)
(13, 13, 104)
sage: all([x^2==169 for x in v])
True
Modulo a power of 2:
sage: R = Integers(2^7); R
Ring of integers modulo 128
sage: a = R(17)
sage: a.sqrt()
23
sage: a.sqrt(all=True)
[23, 41, 87, 105]
sage: [x for x in R if x^2==17]
[23, 41, 87, 105]
Bases: sage.rings.finite_rings.integer_mod.IntegerMod_abstract
Elements of 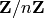 for n small enough to
be operated on in 64 bits
for n small enough to
be operated on in 64 bits
AUTHORS:
Returns True if this is  , otherwise
False.
, otherwise
False.
EXAMPLES:
sage: (mod(-1,5^10)^2).is_one()
True
sage: mod(0,5^10).is_one()
False
Return True iff this element is a unit.
EXAMPLES:
sage: mod(13, 5^10).is_unit()
True
sage: mod(25, 5^10).is_unit()
False
Lift an integer modulo  to the integers.
to the integers.
EXAMPLES:
sage: a = Mod(8943, 2^25); type(a)
<type 'sage.rings.finite_rings.integer_mod.IntegerMod_int64'>
sage: lift(a)
8943
sage: a.lift()
8943
Bases: sage.rings.finite_rings.integer_mod.IntegerMod_hom
Very fast IntegerMod to IntegerMod homomorphism.
EXAMPLES:
sage: from sage.rings.finite_rings.integer_mod import IntegerMod_to_IntegerMod
sage: Rs = [Integers(3**k) for k in range(1,30,5)]
sage: [type(R(0)) for R in Rs]
[<type 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_int64'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_int64'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_gmp'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_gmp'>]
sage: fs = [IntegerMod_to_IntegerMod(S, R) for R in Rs for S in Rs if S is not R and S.order() > R.order()]
sage: all([f(-1) == f.codomain()(-1) for f in fs])
True
sage: [f(-1) for f in fs]
[2, 2, 2, 2, 2, 728, 728, 728, 728, 177146, 177146, 177146, 43046720, 43046720, 10460353202]
Bases: sage.rings.finite_rings.integer_mod.IntegerMod_hom
Fast 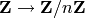 morphism.
morphism.
EXAMPLES:
We make sure it works for every type.
sage: from sage.rings.finite_rings.integer_mod import Integer_to_IntegerMod
sage: Rs = [Integers(10), Integers(10^5), Integers(10^10)]
sage: [type(R(0)) for R in Rs]
[<type 'sage.rings.finite_rings.integer_mod.IntegerMod_int'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_int64'>, <type 'sage.rings.finite_rings.integer_mod.IntegerMod_gmp'>]
sage: fs = [Integer_to_IntegerMod(R) for R in Rs]
sage: [f(-1) for f in fs]
[9, 99999, 9999999999]
Return the equivalence class of  modulo
modulo  as
an element of
as
an element of 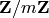 .
.
EXAMPLES:
sage: x = Mod(12345678, 32098203845329048)
sage: x
12345678
sage: x^100
1017322209155072
You can also use the lowercase version:
sage: mod(12,5)
2
Illustrates that trac #5971 is fixed. Consider  modulo
modulo  when
when
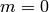 . Then
. Then 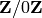 is isomorphic to
is isomorphic to  so
so  modulo
modulo  is
is equivalent to
is
is equivalent to  for any integer value of
for any integer value of  :
:
sage: Mod(10, 0)
10
sage: a = randint(-100, 100)
sage: Mod(a, 0) == a
True
Bases: object
We store the various forms of the modulus here rather than in the parent for efficiency reasons.
We may also store a cached table of all elements of a given ring in this class.
Function to compute and cache all elements of this class.
If inverses==True, also computes and caches the inverses of the invertible elements
Return 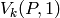 where
where 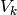 is the Lucas
function defined by the recursive relation
is the Lucas
function defined by the recursive relation
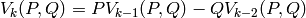
with 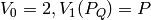 .
.
REFERENCES:
AUTHORS:
TESTS:
sage: from sage.rings.finite_rings.integer_mod import fast_lucas, slow_lucas
sage: all([fast_lucas(k, a) == slow_lucas(k, a)
... for a in Integers(23)
... for k in range(13)])
True
Return True if and only if x is an integer modulo
 .
.
EXAMPLES:
sage: from sage.rings.finite_rings.integer_mod import is_IntegerMod
sage: is_IntegerMod(5)
False
sage: is_IntegerMod(Mod(5,10))
True
Function to convert a Sage Integer into class NativeIntStruct.
Note
This function seems completely redundant, and is not used anywhere.
Return the equivalence class of  modulo
modulo  as
an element of
as
an element of 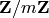 .
.
EXAMPLES:
sage: x = Mod(12345678, 32098203845329048)
sage: x
12345678
sage: x^100
1017322209155072
You can also use the lowercase version:
sage: mod(12,5)
2
Illustrates that trac #5971 is fixed. Consider  modulo
modulo  when
when
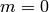 . Then
. Then 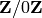 is isomorphic to
is isomorphic to  so
so  modulo
modulo  is
is equivalent to
is
is equivalent to  for any integer value of
for any integer value of  :
:
sage: Mod(10, 0)
10
sage: a = randint(-100, 100)
sage: Mod(a, 0) == a
True
Calculates the square root of  , where
, where  is an
integer mod
is an
integer mod  ; if
; if  is not a perfect square,
this returns an (incorrect) answer without checking.
is not a perfect square,
this returns an (incorrect) answer without checking.
ALGORITHM: Several cases based on residue class of
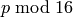 .
.
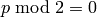 :
: 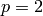 so
so
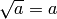 .
.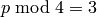 :
: 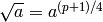 .
.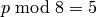 :
: 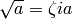 where
where
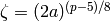 ,
, 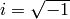 .
.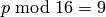 : Similar, work in a bi-quadratic
extension of
: Similar, work in a bi-quadratic
extension of 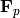 for small
for small  , Tonelli
and Shanks for large
, Tonelli
and Shanks for large  .
.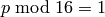 : Tonelli and Shanks.
: Tonelli and Shanks.REFERENCES:
AUTHORS:
TESTS: Every case appears in the first hundred primes.
sage: from sage.rings.finite_rings.integer_mod import square_root_mod_prime # sqrt() uses brute force for small p
sage: all([square_root_mod_prime(a*a)^2 == a*a
... for p in prime_range(100)
... for a in Integers(p)])
True
Calculates the square root of  , where
, where  is an
integer mod
is an
integer mod 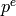 .
.
ALGORITHM: Perform  -adically by stripping off even
powers of
-adically by stripping off even
powers of  to get a unit and lifting
to get a unit and lifting
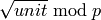 via Newton’s method.
via Newton’s method.
AUTHORS:
EXAMPLES:
sage: from sage.rings.finite_rings.integer_mod import square_root_mod_prime_power
sage: a=Mod(17,2^20)
sage: b=square_root_mod_prime_power(a,2,20)
sage: b^2 == a
True
sage: a=Mod(72,97^10)
sage: b=square_root_mod_prime_power(a,97,10)
sage: b^2 == a
True