AUTHORS:
Bases: sage.structure.element.FieldElement
A floating point approximation to a complex number using any specified precision. Answers derived from calculations with such approximations may differ from what they would be if those calculations were performed with true complex numbers. This is due to the rounding errors inherent to finite precision calculations.
EXAMPLES:
sage: I = CC.0
sage: b = 1.5 + 2.5*I
sage: loads(b.dumps()) == b
True
EXAMPLES:
sage: CC(0).additive_order()
1
sage: CC.gen().additive_order()
+Infinity
Return the Arithmetic-Geometric Mean (AGM) of self and right.
INPUT:
right (complex)– another complex number
- algorithm (string, default “optimal”)– the algorithm to use
(see below).
OUTPUT:
(complex) A value of the AGM of self and right. Note that this is a multi-valued function, and the algorithm used affects the value returned, as follows:
“pari”: Call the sgm function from the pari library.
- “optimal”: Use the AGM sequence such that at each stage
is replaced by
where the sign is chosen so that
, or equivalently
. The resulting limit is maximal among all possible values.
- “principal”: Use the AGM sequence such that at each stage
is replaced by
where the sign is chosen so that
(the so-called principal branch of the square root).
The values
,
, and
are all taken to be 0.
EXAMPLES:
sage: a = CC(1,1)
sage: b = CC(2,-1)
sage: a.agm(b)
1.62780548487271 + 0.136827548397369*I
sage: a.agm(b, algorithm="optimal")
1.62780548487271 + 0.136827548397369*I
sage: a.agm(b, algorithm="principal")
1.62780548487271 + 0.136827548397369*I
sage: a.agm(b, algorithm="pari")
1.62780548487271 + 0.136827548397369*I
An example to show that the returned value depends on the algorithm parameter:
sage: a = CC(-0.95,-0.65)
sage: b = CC(0.683,0.747)
sage: a.agm(b, algorithm="optimal")
-0.371591652351761 + 0.319894660206830*I
sage: a.agm(b, algorithm="principal")
0.338175462986180 - 0.0135326969565405*I
sage: a.agm(b, algorithm="pari")
0.0806891850759812 + 0.239036532685557*I
sage: a.agm(b, algorithm="optimal").abs()
0.490319232466314
sage: a.agm(b, algorithm="principal").abs()
0.338446122230459
sage: a.agm(b, algorithm="pari").abs()
0.252287947683910
TESTS:
An example which came up in testing:
sage: I = CC(I)
sage: a = 0.501648970493109 + 1.11877240294744*I
sage: b = 1.05946309435930 + 1.05946309435930*I
sage: a.agm(b)
0.774901870587681 + 1.10254945079875*I
sage: a = CC(-0.32599972608379413, 0.60395514542928641)
sage: b = CC( 0.6062314525690593, 0.1425693337776659)
sage: a.agm(b)
0.199246281325876 + 0.478401702759654*I
sage: a.agm(-a)
0
sage: a.agm(0)
0
sage: CC(0).agm(a)
0
Consistency:
sage: a = 1 + 0.5*I
sage: b = 2 - 0.25*I
sage: a.agm(b) - ComplexField(100)(a).agm(b)
0
sage: ComplexField(200)(a).agm(b) - ComplexField(500)(a).agm(b)
0
sage: ComplexField(500)(a).agm(b) - ComplexField(1000)(a).agm(b)
0
Returns a polynomial of degree at most  which is
approximately satisfied by this complex number. Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if
which is
approximately satisfied by this complex number. Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if  is a good approximation to an algebraic
number of degree less than
is a good approximation to an algebraic
number of degree less than  .
.
ALGORITHM: Uses the PARI C-library algdep command.
INPUT: Type algdep? at the top level prompt. All additional parameters are passed onto the top-level algdep command.
EXAMPLE:
sage: C = ComplexField()
sage: z = (1/2)*(1 + sqrt(3.0) *C.0); z
0.500000000000000 + 0.866025403784439*I
sage: p = z.algdep(5); p
x^3 + 1
sage: p.factor()
(x + 1) * (x^2 - x + 1)
sage: z^2 - z + 1
1.11022302462516e-16
Returns a polynomial of degree at most  which is
approximately satisfied by this complex number. Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if
which is
approximately satisfied by this complex number. Note that the
returned polynomial need not be irreducible, and indeed usually
won’t be if  is a good approximation to an algebraic
number of degree less than
is a good approximation to an algebraic
number of degree less than  .
.
ALGORITHM: Uses the PARI C-library algdep command.
INPUT: Type algdep? at the top level prompt. All additional parameters are passed onto the top-level algdep command.
EXAMPLE:
sage: C = ComplexField()
sage: z = (1/2)*(1 + sqrt(3.0) *C.0); z
0.500000000000000 + 0.866025403784439*I
sage: p = z.algebraic_dependancy(5); p
x^3 + 1
sage: p.factor()
(x + 1) * (x^2 - x + 1)
sage: z^2 - z + 1
1.11022302462516e-16
EXAMPLES:
sage: (1+CC(I)).arccos()
0.904556894302381 - 1.06127506190504*I
EXAMPLES:
sage: (1+CC(I)).arccosh()
1.06127506190504 + 0.904556894302381*I
EXAMPLES:
sage: ComplexField(100)(1,1).arccoth()
0.40235947810852509365018983331 - 0.55357435889704525150853273009*I
EXAMPLES:
sage: ComplexField(100)(1,1).arccsch()
0.53063753095251782601650945811 - 0.45227844715119068206365839783*I
EXAMPLES:
sage: ComplexField(100)(1,1).arcsech()
-0.53063753095251782601650945811 + 1.1185178796437059371676632938*I
EXAMPLES:
sage: (1+CC(I)).arcsin()
0.666239432492515 + 1.06127506190504*I
EXAMPLES:
sage: (1+CC(I)).arcsinh()
1.06127506190504 + 0.666239432492515*I
EXAMPLES:
sage: (1+CC(I)).arctan()
1.01722196789785 + 0.402359478108525*I
EXAMPLES:
sage: (1+CC(I)).arctanh()
0.402359478108525 + 1.01722196789785*I
Same as argument.
EXAMPLES:
sage: i = CC.0
sage: (i^2).arg()
3.14159265358979
The argument (angle) of the complex number, normalized so that
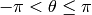 .
.
EXAMPLES:
sage: i = CC.0
sage: (i^2).argument()
3.14159265358979
sage: (1+i).argument()
0.785398163397448
sage: i.argument()
1.57079632679490
sage: (-i).argument()
-1.57079632679490
sage: (RR('-0.001') - i).argument()
-1.57179632646156
Return the complex conjugate of this complex number.
EXAMPLES:
sage: i = CC.0
sage: (1+i).conjugate()
1.00000000000000 - 1.00000000000000*I
EXAMPLES:
sage: (1+CC(I)).cos()
0.833730025131149 - 0.988897705762865*I
EXAMPLES:
sage: (1+CC(I)).cosh()
0.833730025131149 + 0.988897705762865*I
EXAMPLES:
sage: (1+CC(I)).cotan()
0.217621561854403 - 0.868014142895925*I
sage: i = ComplexField(200).0
sage: (1+i).cotan()
0.21762156185440268136513424360523807352075436916785404091068 - 0.86801414289592494863584920891627388827343874994609327121115*I
sage: i = ComplexField(220).0
sage: (1+i).cotan()
0.21762156185440268136513424360523807352075436916785404091068124239 - 0.86801414289592494863584920891627388827343874994609327121115071646*I
EXAMPLES:
sage: ComplexField(100)(1,1).coth()
0.86801414289592494863584920892 - 0.21762156185440268136513424361*I
EXAMPLES:
sage: ComplexField(100)(1,1).csc()
0.62151801717042842123490780586 - 0.30393100162842645033448560451*I
EXAMPLES:
sage: ComplexField(100)(1,1).csch()
0.30393100162842645033448560451 - 0.62151801717042842123490780586*I
Returns the complex dilogarithm of self. The complex dilogarithm, or Spence’s function, is defined by
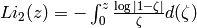
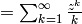
Note that the series definition can only be used for
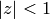
EXAMPLES:
sage: a = ComplexNumber(1,0)
sage: a.dilog()
1.64493406684823
sage: float(pi^2/6)
1.6449340668482262
sage: b = ComplexNumber(0,1)
sage: b.dilog()
-0.205616758356028 + 0.915965594177219*I
sage: c = ComplexNumber(0,0)
sage: c.dilog()
0
Return the value of the Dedekind 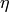 function on self,
intelligently computed using
function on self,
intelligently computed using 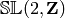 transformations.
transformations.
INPUT:
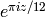 factor.
factor.OUTPUT: a complex number
The 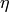 function is
function is
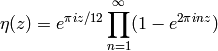
ALGORITHM: Uses the PARI C library.
EXAMPLES:
First we compute 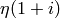 :
:
sage: i = CC.0
sage: z = 1+i; z.eta()
0.742048775836565 + 0.198831370229911*I
We compute eta to low precision directly from the definition.
sage: z = 1 + i; z.eta()
0.742048775836565 + 0.198831370229911*I
sage: pi = CC(pi) # otherwise we will get a symbolic result.
sage: exp(pi * i * z / 12) * prod([1-exp(2*pi*i*n*z) for n in range(1,10)])
0.742048775836565 + 0.198831370229911*I
The optional argument allows us to omit the fractional part:
sage: z = 1 + i
sage: z.eta(omit_frac=True)
0.998129069925959 - 8.12769318...e-22*I
sage: prod([1-exp(2*pi*i*n*z) for n in range(1,10)])
0.998129069925958 + 4.59099857829247e-19*I
We illustrate what happens when  is not in the upper
half plane.
is not in the upper
half plane.
sage: z = CC(1)
sage: z.eta()
...
ValueError: value must be in the upper half plane
You can also use functional notation.
sage: eta(1+CC(I))
0.742048775836565 + 0.198831370229911*I
Compute exp(z).
EXAMPLES:
sage: i = ComplexField(300).0
sage: z = 1 + i
sage: z.exp()
1.46869393991588515713896759732660426132695673662900872279767567631093696585951213872272450 + 2.28735528717884239120817190670050180895558625666835568093865811410364716018934540926734485*I
Return the Gamma function evaluated at this complex number.
EXAMPLES:
sage: i = ComplexField(30).0
sage: (1+i).gamma()
0.49801567 - 0.15494983*I
TESTS:
sage: CC(0).gamma()
Infinity
sage: CC(-1).gamma()
Infinity
Return the incomplete Gamma function evaluated at this complex number.
EXAMPLES:
sage: C, i = ComplexField(30).objgen()
sage: (1+i).gamma_inc(2 + 3*i)
0.0020969149 - 0.059981914*I
sage: (1+i).gamma_inc(5)
-0.0013781309 + 0.0065198200*I
sage: C(2).gamma_inc(1 + i)
0.70709210 - 0.42035364*I
sage: CC(2).gamma_inc(5)
0.0404276819945128
Return imaginary part of self.
EXAMPLES:
sage: i = ComplexField(100).0
sage: z = 2 + 3*i
sage: x = z.imag(); x
3.0000000000000000000000000000
sage: x.parent()
Real Field with 100 bits of precision
sage: z.imag_part()
3.0000000000000000000000000000
Return imaginary part of self.
EXAMPLES:
sage: i = ComplexField(100).0
sage: z = 2 + 3*i
sage: x = z.imag(); x
3.0000000000000000000000000000
sage: x.parent()
Real Field with 100 bits of precision
sage: z.imag_part()
3.0000000000000000000000000000
Return True if self is imaginary, i.e. has real part zero.
EXAMPLES:
sage: CC(1.23*i).is_imaginary()
True
sage: CC(1+i).is_imaginary()
False
Return True if self is real, i.e. has imaginary part zero.
EXAMPLES:
sage: CC(1.23).is_real()
True
sage: CC(1+i).is_real()
False
This function always returns true as 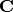 is
algebraically closed.
is
algebraically closed.
EXAMPLES:
sage: a = ComplexNumber(2,1)
sage: a.is_square()
True
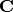 is algebraically closed, hence every element
is a square:
is algebraically closed, hence every element
is a square:
sage: b = ComplexNumber(5)
sage: b.is_square()
True
Complex logarithm of z with branch chosen as follows: Write
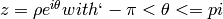 . Then
. Then
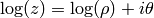 .
.
Warning
Currently the real log is computed using floats, so there is potential precision loss.
EXAMPLES:
sage: a = ComplexNumber(2,1)
sage: a.log()
0.804718956217050 + 0.463647609000806*I
sage: log(a.abs())
0.804718956217050
sage: a.argument()
0.463647609000806
sage: b = ComplexNumber(float(exp(42)),0)
sage: b.log()
41.99999999999971
sage: c = ComplexNumber(-1,0)
sage: c.log()
3.14159265358979*I
The option of a base is included for compatibility with other logs:
sage: c = ComplexNumber(-1,0)
sage: c.log(2)
4.53236014182719*I
Return the multiplicative order of this complex number, if known, or raise a NotImplementedError.
EXAMPLES:
sage: C.<i> = ComplexField()
sage: i.multiplicative_order()
4
sage: C(1).multiplicative_order()
1
sage: C(-1).multiplicative_order()
2
sage: C(i^2).multiplicative_order()
2
sage: C(-i).multiplicative_order()
4
sage: C(2).multiplicative_order()
+Infinity
sage: w = (1+sqrt(-3.0))/2; w
0.500000000000000 + 0.866025403784439*I
sage: abs(w)
1.00000000000000
sage: w.multiplicative_order()
...
NotImplementedError: order of element not known
Returns the norm of this complex number. If 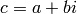 is a
complex number, then the norm of
is a
complex number, then the norm of  is defined as
is defined as
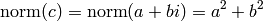
The norm of a complex number is different from its absolute value.
The absolute value of a complex number is defined to be the square
root of its norm. A typical use of the complex norm is in the
integral domain ![\ZZ[i]](../../_images/math/0804e0e7b83cafcf84a0606c92c26c327125e125.png) of Gaussian integers, where the norm of
each Gaussian integer
of Gaussian integers, where the norm of
each Gaussian integer 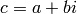 is defined as its complex norm.
is defined as its complex norm.
EXAMPLES:
This indeed acts as the square function when the imaginary component of self is equal to zero:
sage: a = ComplexNumber(2,1)
sage: a.norm()
5.00000000000000
sage: b = ComplexNumber(4.2,0)
sage: b.norm()
17.6400000000000
sage: b^2
17.6400000000000
The n-th root function.
INPUT:
EXAMPLES:
sage: a = CC(27)
sage: a.nth_root(3)
3.00000000000000
sage: a.nth_root(3, all=True)
[3.00000000000000, -1.50000000000000 + 2.59807621135332*I, -1.50000000000000 - 2.59807621135332*I]
sage: a = ComplexField(20)(2,1)
sage: [r^7 for r in a.nth_root(7, all=True)]
[2.0000 + 1.0000*I, 2.0000 + 1.0000*I, 2.0000 + 1.0000*I, 2.0000 + 1.0000*I, 2.0000 + 1.0000*I, 2.0000 + 1.0001*I, 2.0000 + 1.0001*I]
Plots this complex number as a point in the plane
The accepted options are the ones of point2d(). Type point2d.options to see all options.
Note
Just wraps the sage.plot.point.point2d method
EXAMPLES:
You can either use the indirect:
sage: z = CC(0,1)
sage: plot(z)
or the more direct:
sage: z = CC(0,1)
sage: z.plot()
Return precision of this complex number.
EXAMPLES:
sage: i = ComplexField(2000).0
sage: i.prec()
2000
Return real part of self.
EXAMPLES:
sage: i = ComplexField(100).0
sage: z = 2 + 3*i
sage: x = z.real(); x
2.0000000000000000000000000000
sage: x.parent()
Real Field with 100 bits of precision
sage: z.real_part()
2.0000000000000000000000000000
Return real part of self.
EXAMPLES:
sage: i = ComplexField(100).0
sage: z = 2 + 3*i
sage: x = z.real(); x
2.0000000000000000000000000000
sage: x.parent()
Real Field with 100 bits of precision
sage: z.real_part()
2.0000000000000000000000000000
EXAMPLES:
sage: ComplexField(100)(1,1).sec()
0.49833703055518678521380589177 + 0.59108384172104504805039169297*I
EXAMPLES:
sage: ComplexField(100)(1,1).sech()
0.49833703055518678521380589177 - 0.59108384172104504805039169297*I
EXAMPLES:
sage: (1+CC(I)).sin()
1.29845758141598 + 0.634963914784736*I
EXAMPLES:
sage: (1+CC(I)).sinh()
0.634963914784736 + 1.29845758141598*I
The square root function, taking the branch cut to be the negative real axis.
INPUT:
EXAMPLES:
sage: C.<i> = ComplexField(30)
sage: i.sqrt()
0.70710678 + 0.70710678*I
sage: (1+i).sqrt()
1.0986841 + 0.45508986*I
sage: (C(-1)).sqrt()
1.0000000*I
sage: (1 + 1e-100*i).sqrt()^2
1.0000000 + 1.0000000e-100*I
sage: i = ComplexField(200).0
sage: i.sqrt()
0.70710678118654752440084436210484903928483593768847403658834 + 0.70710678118654752440084436210484903928483593768847403658834*I
Return a string representation of this number.
INPUTS:
EXAMPLES:
sage: a = CC(pi + I*e)
sage: a.str()
'3.14159265358979 + 2.71828182845905*I'
sage: a.str(truncate=False)
'3.1415926535897931 + 2.7182818284590451*I'
sage: a.str(base=2)
'11.001001000011111101101010100010001000010110100011000 + 10.101101111110000101010001011000101000101011101101001*I'
sage: CC(0.5 + 0.625*I).str(base=2)
'0.10000000000000000000000000000000000000000000000000000 + 0.10100000000000000000000000000000000000000000000000000*I'
sage: a.str(base=16)
'3.243f6a8885a30 + 2.b7e151628aed2*I'
sage: a.str(base=36)
'3.53i5ab8p5fc + 2.puw5nggjf8f*I'
EXAMPLES:
sage: (1+CC(I)).tan()
0.271752585319512 + 1.08392332733869*I
EXAMPLES:
sage: (1+CC(I)).tanh()
1.08392332733869 + 0.271752585319512*I
Return the Riemann zeta function evaluated at this complex number.
EXAMPLES:
sage: i = ComplexField(30).gen()
sage: z = 1 + i
sage: z.zeta()
0.58215806 - 0.92684856*I
sage: zeta(z)
0.58215806 - 0.92684856*I
Returns -1, 0, or 1 according to whether 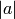 is less than, equal to, or greater than
is less than, equal to, or greater than 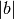 .
.
Optimized for non-close numbers, where the ordering can be determined by examining exponents.
EXAMPLES:
sage: from sage.rings.complex_number import cmp_abs
sage: cmp_abs(CC(5), CC(1))
1
sage: cmp_abs(CC(5), CC(4))
1
sage: cmp_abs(CC(5), CC(5))
0
sage: cmp_abs(CC(5), CC(6))
-1
sage: cmp_abs(CC(5), CC(100))
-1
sage: cmp_abs(CC(-100), CC(1))
1
sage: cmp_abs(CC(-100), CC(100))
0
sage: cmp_abs(CC(-100), CC(1000))
-1
sage: cmp_abs(CC(1,1), CC(1))
1
sage: cmp_abs(CC(1,1), CC(2))
-1
sage: cmp_abs(CC(1,1), CC(1,0.99999))
1
sage: cmp_abs(CC(1,1), CC(1,-1))
0
sage: cmp_abs(CC(0), CC(1))
-1
sage: cmp_abs(CC(1), CC(0))
1
sage: cmp_abs(CC(0), CC(0))
0
sage: cmp_abs(CC(2,1), CC(1,2))
0
Return the complex number defined by the strings s_real and s_imag as an element of ComplexField(prec=n), where n potentially has slightly more (controlled by pad) bits than given by s.
INPUT:
EXAMPLES:
sage: ComplexNumber('2.3')
2.30000000000000
sage: ComplexNumber('2.3','1.1')
2.30000000000000 + 1.10000000000000*I
sage: ComplexNumber(10)
10.0000000000000
sage: ComplexNumber(10,10)
10.0000000000000 + 10.0000000000000*I
sage: ComplexNumber(1.000000000000000000000000000,2)
1.00000000000000000000000000 + 2.00000000000000000000000000*I
sage: ComplexNumber(1,2.000000000000000000000)
1.00000000000000000000 + 2.00000000000000000000*I
sage: sage.rings.complex_number.create_ComplexNumber(s_real=2,s_imag=1)
2.00000000000000 + 1.00000000000000*I
Returns True if x is a complex number. In particular, if x is of the ComplexNumber type.
EXAMPLES:
sage: from sage.rings.complex_number import is_ComplexNumber
sage: a = ComplexNumber(1,2); a
1.00000000000000 + 2.00000000000000*I
sage: is_ComplexNumber(a)
True
sage: b = ComplexNumber(1); b
1.00000000000000
sage: is_ComplexNumber(b)
True
Note that the global element I is of type SymbolicConstant. However, elements of the class ComplexField_class are of type ComplexNumber:
sage: c = 1 + 2*I
sage: is_ComplexNumber(c)
False
sage: d = CC(1 + 2*I)
sage: is_ComplexNumber(d)
True