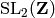Congruence arithmetic subgroups of ${\rm SL}_2(\ZZ)$ ¶

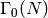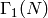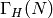Sage can compute extensively with the standard congruence subgroups $\Gamma_0(N)$ , $\Gamma_1(N)$ , and $\Gamma_H(N)$ .

AUTHOR:: – William Stein

class sage.modular.arithgroup.congroup_generic.CongruenceSubgroup(level)¶

Bases: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup

is_congruence()¶

Return True, since this is a congruence subgroup.

EXAMPLE:

sage: Gamma0(7).is_congruence()
True

level()¶

Return the level of this congruence subgroup.

EXAMPLES:

sage: SL2Z.level()
1
sage: Gamma0(20).level()
20
sage: Gamma1(11).level()
11
sage: GammaH(14, [5]).level()
14

modular_abelian_variety()¶

Return the modular abelian variety corresponding to the congruence subgroup self.

EXAMPLES:

sage: Gamma0(11).modular_abelian_variety()
Abelian variety J0(11) of dimension 1
sage: Gamma1(11).modular_abelian_variety()
Abelian variety J1(11) of dimension 1
sage: GammaH(11,[3]).modular_abelian_variety()
Abelian variety JH(11,[3]) of dimension 1

modular_symbols(sign=0, weight=2, base_ring=Rational Field)¶

Return the space of modular symbols of the specified weight and sign on the congruence subgroup self.

EXAMPLES:

sage: G = Gamma0(23)
sage: G.modular_symbols()
Modular Symbols space of dimension 5 for Gamma_0(23) of weight 2 with sign 0 over Rational Field
sage: G.modular_symbols(weight=4)
Modular Symbols space of dimension 12 for Gamma_0(23) of weight 4 with sign 0 over Rational Field
sage: G.modular_symbols(base_ring=GF(7))
Modular Symbols space of dimension 5 for Gamma_0(23) of weight 2 with sign 0 over Finite Field of size 7
sage: G.modular_symbols(sign=1)
Modular Symbols space of dimension 3 for Gamma_0(23) of weight 2 with sign 1 over Rational Field

sturm_bound(weight=2)¶

Returns the Sturm bound for modular forms of the given weight and level this congruence subgroup.

INPUT:

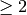weight - an integer $\geq 2$ (default: 2)

EXAMPLES::: sage: Gamma0(11).sturm_bound(2) 2 sage: Gamma0(389).sturm_bound(2) 65 sage: Gamma0(1).sturm_bound(12) 1 sage: Gamma0(100).sturm_bound(2) 30 sage: Gamma0(1).sturm_bound(36) 3 sage: Gamma0(11).sturm_bound() 2 sage: Gamma0(13).sturm_bound() 3 sage: Gamma0(16).sturm_bound() 4 sage: GammaH(16,[13]).sturm_bound() 8 sage: GammaH(16,[15]).sturm_bound() 16 sage: Gamma1(16).sturm_bound() 32 sage: Gamma1(13).sturm_bound() 28 sage: Gamma1(13).sturm_bound(5) 70

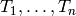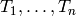FURTHER DETAILS: This function returns a positive integer $n$ such that the Hecke operators $T_1,\ldots, T_n$ acting on cusp forms generate the Hecke algebra as a $\ZZ$ -module when the character is trivial or quadratic. Otherwise, $T_1,\ldots,T_n$ generate the Hecke algebra at least as a $\ZZ[\varepsilon]$ -module, where $\ZZ[\varepsilon]$ is the ring generated by the values of the Dirichlet character $\varepsilon$ . 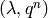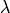Alternatively, this is a bound such that if two cusp forms associated to this space of modular symbols are congruent modulo $(\lambda, q^n)$ , then they are congruent modulo $\lambda$ .

REFERENCES:

See the Agashe-Stein appendix to Lario and Schoof, Some computations with Hecke rings and deformation rings, Experimental Math., 11 (2002), no. 2, 303-311.
This result originated in the paper Sturm, On the congruence of modular forms, Springer LNM 1240, 275-280, 1987.

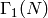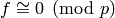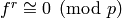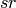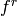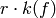REMARK: Kevin Buzzard pointed out to me (William Stein) in Fall 2002 that the above bound is fine for $\Gamma_1(N)$ with character, as one sees by taking a power of $f$ . More precisely, if $f \cong 0 \pmod{p}$ for first $s$ coefficients, then $f^r \cong 0 \pmod{p}$ for first $sr$ coefficients. 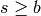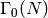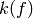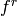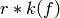Since the weight of $f^r$ is $r\cdot k(f)$ , it follows that if $s \geq b$ , where $b$ is the Sturm bound for $\Gamma_0(N)$ at weight $k(f)$ , then $f^r$ has valuation large enough to be forced to be $0$ at $r*k(f)$ by Sturm bound (which is valid if we choose $r$ correctly). 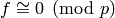Thus $f \cong 0 \pmod{p}$ . 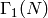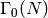Conclusion: For $\Gamma_1(N)$ with fixed character, the Sturm bound is exactly the same as for $\Gamma_0(N)$ .

A key point is that we are finding $\ZZ[\varepsilon]$ generators for the Hecke algebra here, not $\ZZ$ -generators. So if one wants generators for the Hecke algebra over $\ZZ$ , this bound must be suitably modified (and I’m not sure what the modification is).

AUTHORS:

William Stein

sage.modular.arithgroup.congroup_generic.is_CongruenceSubgroup(x)¶

Return True if x is of type CongruenceSubgroup.

EXAMPLES:

sage: from sage.modular.arithgroup.congroup_generic import is_CongruenceSubgroup
sage: is_CongruenceSubgroup(SL2Z)
True
sage: is_CongruenceSubgroup(Gamma0(13))
True
sage: is_CongruenceSubgroup(Gamma1(6))
True
sage: is_CongruenceSubgroup(GammaH(11, [3]))
True
sage: is_CongruenceSubgroup(SymmetricGroup(3))
False

Congruence arithmetic subgroups of ${\rm SL}_2(\ZZ)$ ¶

Previous topic

Next topic

This Page

Navigation

Congruence arithmetic subgroups of ¶

Previous topic

Next topic

This Page

Quick search

Navigation

Congruence arithmetic subgroups of ${\rm SL}_2(\ZZ)$ ¶