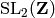 ¶
¶Sage can compute extensively with the standard congruence subgroups
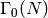 ,
, 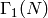 , and
, and 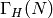 .
.
Bases: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup
Return True, since this is a congruence subgroup.
EXAMPLE:
sage: Gamma0(7).is_congruence()
True
Return the level of this congruence subgroup.
EXAMPLES:
sage: SL2Z.level()
1
sage: Gamma0(20).level()
20
sage: Gamma1(11).level()
11
sage: GammaH(14, [5]).level()
14
Return the modular abelian variety corresponding to the congruence subgroup self.
EXAMPLES:
sage: Gamma0(11).modular_abelian_variety()
Abelian variety J0(11) of dimension 1
sage: Gamma1(11).modular_abelian_variety()
Abelian variety J1(11) of dimension 1
sage: GammaH(11,[3]).modular_abelian_variety()
Abelian variety JH(11,[3]) of dimension 1
Return the space of modular symbols of the specified weight and sign on the congruence subgroup self.
EXAMPLES:
sage: G = Gamma0(23)
sage: G.modular_symbols()
Modular Symbols space of dimension 5 for Gamma_0(23) of weight 2 with sign 0 over Rational Field
sage: G.modular_symbols(weight=4)
Modular Symbols space of dimension 12 for Gamma_0(23) of weight 4 with sign 0 over Rational Field
sage: G.modular_symbols(base_ring=GF(7))
Modular Symbols space of dimension 5 for Gamma_0(23) of weight 2 with sign 0 over Finite Field of size 7
sage: G.modular_symbols(sign=1)
Modular Symbols space of dimension 3 for Gamma_0(23) of weight 2 with sign 1 over Rational Field
Returns the Sturm bound for modular forms of the given weight and level this congruence subgroup.
INPUT:
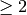 (default: 2)
(default: 2)FURTHER DETAILS: This function returns a positive integer
 such that the Hecke operators
such that the Hecke operators
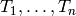 acting on cusp forms generate the
Hecke algebra as a
acting on cusp forms generate the
Hecke algebra as a 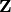 -module when the character
is trivial or quadratic. Otherwise,
-module when the character
is trivial or quadratic. Otherwise, 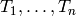 generate the Hecke algebra at least as a
generate the Hecke algebra at least as a
![\ZZ[\varepsilon]](../../../_images/math/b73b4ad09f071ef41a791b826ef92b6842af74fe.png) -module, where
-module, where
![\ZZ[\varepsilon]](../../../_images/math/b73b4ad09f071ef41a791b826ef92b6842af74fe.png) is the ring generated by the
values of the Dirichlet character
is the ring generated by the
values of the Dirichlet character  .
Alternatively, this is a bound such that if two cusp forms
associated to this space of modular symbols are congruent modulo
.
Alternatively, this is a bound such that if two cusp forms
associated to this space of modular symbols are congruent modulo
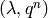 , then they are congruent modulo
, then they are congruent modulo
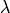 .
.
REFERENCES:
REMARK: Kevin Buzzard pointed out to me (William Stein) in Fall
2002 that the above bound is fine for 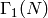 with
character, as one sees by taking a power of
with
character, as one sees by taking a power of 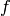 . More
precisely, if
. More
precisely, if 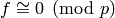 for first
for first
 coefficients, then
coefficients, then 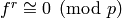 for
first
for
first 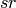 coefficients. Since the weight of
coefficients. Since the weight of 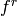 is
is 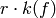 , it follows that if
, it follows that if
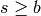 , where
, where 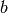 is the Sturm bound for
is the Sturm bound for
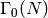 at weight
at weight 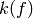 , then
, then 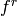 has valuation large enough to be forced to be
has valuation large enough to be forced to be 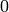 at
at
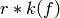 by Sturm bound (which is valid if we choose
by Sturm bound (which is valid if we choose
 correctly). Thus
correctly). Thus 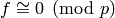 .
Conclusion: For
.
Conclusion: For 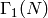 with fixed character, the
Sturm bound is exactly the same as for
with fixed character, the
Sturm bound is exactly the same as for 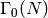 .
.
A key point is that we are finding
![\ZZ[\varepsilon]](../../../_images/math/b73b4ad09f071ef41a791b826ef92b6842af74fe.png) generators for the Hecke algebra
here, not
generators for the Hecke algebra
here, not 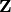 -generators. So if one wants
generators for the Hecke algebra over
-generators. So if one wants
generators for the Hecke algebra over 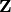 , this
bound must be suitably modified (and I’m not sure what the
modification is).
, this
bound must be suitably modified (and I’m not sure what the
modification is).
AUTHORS:
Return True if x is of type CongruenceSubgroup.
EXAMPLES:
sage: from sage.modular.arithgroup.congroup_generic import is_CongruenceSubgroup
sage: is_CongruenceSubgroup(SL2Z)
True
sage: is_CongruenceSubgroup(Gamma0(13))
True
sage: is_CongruenceSubgroup(Gamma1(6))
True
sage: is_CongruenceSubgroup(GammaH(11, [3]))
True
sage: is_CongruenceSubgroup(SymmetricGroup(3))
False