 ¶
¶AUTHORS:
Bases: sage.modular.arithgroup.congroup_generic.CongruenceSubgroup
The congruence subgroup 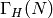 for some subgroup
for some subgroup 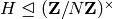 , which is the subgroup of
, which is the subgroup of 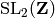 consisting of matrices of the form
consisting of matrices of the form 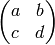 with
with 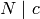 and
and 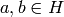 .
.
TESTS:
We test calculation of various invariants of the group:
sage: GammaH(33,[2]).projective_index()
96
sage: GammaH(33,[2]).genus()
5
sage: GammaH(7,[2]).genus()
0
sage: GammaH(23, [1..22]).genus()
2
sage: Gamma0(23).genus()
2
sage: GammaH(23, [1]).genus()
12
sage: Gamma1(23).genus()
12
We calculate the dimensions of some modular forms spaces:
sage: GammaH(33,[2]).dimension_cusp_forms(2)
5
sage: GammaH(33,[2]).dimension_cusp_forms(3)
0
sage: GammaH(33,[2,5]).dimension_cusp_forms(2)
3
sage: GammaH(32079, [21676]).dimension_cusp_forms(20)
180266112
We can sometimes show that there are no weight 1 cusp forms:
sage: GammaH(20, [9]).dimension_cusp_forms(1)
0
Return a set of coset representatives for self \ SL2Z.
EXAMPLES:
sage: list(Gamma1(3).coset_reps())
[[1 0]
[0 1], [-1 -2]
[ 3 5], [ 0 -1]
[ 1 0], [-2 1]
[ 5 -3], [1 0]
[1 1], [-3 -2]
[ 8 5], [ 0 -1]
[ 1 2], [-2 -3]
[ 5 7]]
sage: len(list(Gamma1(31).coset_reps())) == 31**2 - 1
True
Return the dimension of the space of new (or  -new)
weight
-new)
weight  cusp forms for this congruence subgroup.
cusp forms for this congruence subgroup.
INPUT:
 -new subspace.
-new subspace.OUTPUT: Integer
EXAMPLES:
sage: GammaH(33,[2]).dimension_new_cusp_forms()
3
sage: Gamma1(4*25).dimension_new_cusp_forms(2, p=5)
225
sage: Gamma1(33).dimension_new_cusp_forms(2)
19
sage: Gamma1(33).dimension_new_cusp_forms(2,p=11)
21
Given this congruence subgroup 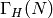 , return all
subgroups
, return all
subgroups 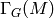 for
for  a divisor of
a divisor of  and such that
and such that
 is equal to the image of
is equal to the image of 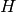 modulo
modulo  .
.
EXAMPLES:
sage: G = GammaH(33,[2]); G
Congruence Subgroup Gamma_H(33) with H generated by [2]
sage: G._list_of_elements_in_H()
[1, 2, 4, 8, 16, 17, 25, 29, 31, 32]
sage: G.divisor_subgroups()
[Modular Group SL(2,Z),
Congruence Subgroup Gamma_H(3) with H generated by [2],
Congruence Subgroup Gamma_H(11) with H generated by [2],
Congruence Subgroup Gamma_H(33) with H generated by [2]]
Return a set of coset representatives for self \ Gamma0(N), where N is the level of self.
EXAMPLE:
sage: GammaH(108, [1,-1]).gamma0_coset_reps()
[[1 0] [0 1], [-43 -45] [108 113], [ 31 33] [108 115], [-49 -54]
[108 119], [ 25 28] [108 121], [-19 -22] [108 125], [-17 -20] [108
127], [ 47 57] [108 131], [ 13 16] [108 133], [ 41 52] [108
137], [ 7 9] [108 139], [-37 -49] [108 143], [-35 -47] [108
145], [ 29 40] [108 149], [ -5 -7] [108 151], [ 23 33] [108
155], [-11 -16] [108 157], [ 53 79] [108 161]]
Return generators for this congruence subgroup.
The result is cached.
EXAMPLE:
sage: for g in GammaH(3, [2]).generators():
... print g
... print '---'
[1 1]
[0 1]
---
[-1 0]
[ 0 -1]
---
[ 1 -1]
[ 0 1]
---
[1 0]
[3 1]
---
[1 1]
[0 1]
---
[-1 0]
[ 3 -1]
---
[ 1 0]
[-3 1]
---
Return the index of self in SL2Z.
EXAMPLE:
sage: [G.index() for G in Gamma0(40).gamma_h_subgroups()]
[72, 144, 144, 144, 144, 288, 288, 288, 288, 144, 288, 288, 576, 576, 144, 288, 288, 576, 576, 144, 288, 288, 576, 576, 288, 576, 1152]
Return True precisely if this subgroup contains the matrix -1.
EXAMPLES:
sage: GammaH(10, [3]).is_even()
True
sage: GammaH(14, [1]).is_even()
False
Return True if self is a subgroup of right, and False otherwise.
EXAMPLES:
sage: GammaH(24,[7]).is_subgroup(SL2Z)
True
sage: GammaH(24,[7]).is_subgroup(Gamma0(8))
True
sage: GammaH(24, []).is_subgroup(GammaH(24, [7]))
True
sage: GammaH(24, []).is_subgroup(Gamma1(24))
True
sage: GammaH(24, [17]).is_subgroup(GammaH(24, [7]))
False
sage: GammaH(1371, [169]).is_subgroup(GammaH(457, [169]))
True
Return the number of orbits of cusps (regular or otherwise) for this subgroup.
EXAMPLE:
sage: GammaH(33,[2]).ncusps()
8
sage: GammaH(32079, [21676]).ncusps()
28800
AUTHORS:
Return the number of irregular cusps for this subgroup.
EXAMPLES:
sage: GammaH(3212, [2045, 2773]).nirregcusps()
720
Return the number of orbits of regular cusps for this subgroup. A cusp is regular if we may find a parabolic element generating the stabiliser of that cusp whose eigenvalues are both +1 rather than -1. If G contains -1, all cusps are regular.
EXAMPLES:
sage: GammaH(20, [17]).nregcusps()
4
sage: GammaH(20, [17]).nirregcusps()
2
sage: GammaH(3212, [2045, 2773]).nregcusps()
1440
sage: GammaH(3212, [2045, 2773]).nirregcusps()
720
AUTHOR:
Return the number of orbits of elliptic points of order 2 for this group.
EXAMPLE:
sage: [H.nu2() for n in [1..10] for H in Gamma0(n).gamma_h_subgroups()]
[1, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0]
sage: GammaH(33,[2]).nu2()
0
sage: GammaH(5,[2]).nu2()
2
AUTHORS:
Return the number of orbits of elliptic points of order 3 for this group.
EXAMPLE:
sage: [H.nu3() for n in [1..10] for H in Gamma0(n).gamma_h_subgroups()]
[1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
sage: GammaH(33,[2]).nu3()
0
sage: GammaH(7,[2]).nu3()
2
AUTHORS:
Compute a minimal representative for the given cusp c. Returns a cusp c’ which is equivalent to the given cusp, and is in lowest terms with minimal positive denominator, and minimal positive numerator for that denominator.
Two cusps 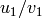 and
and 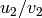 are equivalent modulo
are equivalent modulo 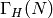 if and only if
if and only if
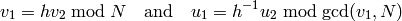
or
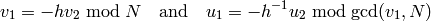
for some 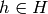 .
.
EXAMPLES:
sage: GammaH(6,[5]).reduce_cusp(Cusp(5,3))
1/3
sage: GammaH(12,[5]).reduce_cusp(Cusp(8,9))
1/3
sage: GammaH(12,[5]).reduce_cusp(Cusp(5,12))
Infinity
sage: GammaH(12,[]).reduce_cusp(Cusp(5,12))
5/12
sage: GammaH(21,[5]).reduce_cusp(Cusp(-9/14))
1/7
Return the subgroup of 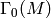 obtained by taking
obtained by taking 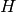 to
be the image of the
to
be the image of the 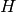 at level
at level  modulo
modulo  .
.
EXAMPLES:
sage: G = GammaH(33,[2])
sage: G.restrict(11)
Congruence Subgroup Gamma_H(11) with H generated by [2]
sage: G.restrict(1)
Modular Group SL(2,Z)
sage: G.restrict(15)
...
ValueError: M (=15) must be a divisor of the level (33) of self
Return the congruence subgroup 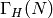 , which is the subgroup of
, which is the subgroup of
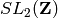 consisting of matrices of the form
consisting of matrices of the form 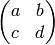 with
with 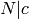 and
and 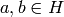 , for
, for 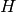 a specified
subgroup of
a specified
subgroup of 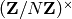 .
.
INPUT:
level – an integer
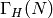 , where
, where 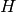 is the subgroup of
is the subgroup of 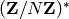 generated by the
elements of the list.
generated by the
elements of the list.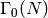 .
.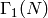 .
.EXAMPLES:
sage: GammaH(11,0) # indirect doctest
Congruence Subgroup Gamma0(11)
sage: GammaH(11,1)
Congruence Subgroup Gamma1(11)
sage: GammaH(11,[2])
Congruence Subgroup Gamma_H(11) with H generated by [2]
sage: GammaH(11,[2,1])
Congruence Subgroup Gamma_H(11) with H generated by [2]
sage: GammaH(14,[10])
...
ArithmeticError: The generators [10] must be units modulo 14
Return True if x is a congruence subgroup of type GammaH.
EXAMPLES:
sage: from sage.modular.arithgroup.all import is_GammaH
sage: is_GammaH(GammaH(13, [2]))
True
sage: is_GammaH(Gamma0(6))
True
sage: is_GammaH(sage.modular.arithgroup.congroup_generic.CongruenceSubgroup(5))
False
Return 0 if any cube divides  . Otherwise return
. Otherwise return
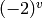 where
where  is the number of primes that
exactly divide
is the number of primes that
exactly divide  .
.
This is similar to the Moebius function.
INPUT:
OUTPUT: Integer
EXAMPLES:
sage: from sage.modular.arithgroup.congroup_gammaH import mumu
sage: mumu(27)
0
sage: mumu(6*25)
4
sage: mumu(7*9*25)
-2
sage: mumu(9*25)
1