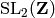 )¶
)¶Bases: sage.groups.group.Group
Base class for arithmetic subgroups of 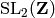 . Not
intended to be used directly, but still includes quite a few
general-purpose routines which compute data about an arithmetic subgroup
assuming that it has a working element testing routine.
. Not
intended to be used directly, but still includes quite a few
general-purpose routines which compute data about an arithmetic subgroup
assuming that it has a working element testing routine.
Determine whether  and
and  are equivalent by an element of
self, i.e. whether or not there exists an element
are equivalent by an element of
self, i.e. whether or not there exists an element 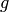 of self
such that
of self
such that 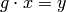 .
.
NOTE: This function should be overridden by all subclasses.
EXAMPLES:
sage: sage.modular.arithgroup.congroup_generic.CongruenceSubgroup(5).are_equivalent(0, 0)
...
NotImplementedError
Test whether or not cusps x and y are equivalent modulo self. If self has a reduce_cusp() method, use that; otherwise do a slow explicit test.
If trans = False, returns True or False. If trans = True, then return either False or an element of self mapping x onto y.
EXAMPLE:
sage: Gamma0(7).are_equivalent_cusps(Cusp(1/3), Cusp(0), trans=True)
[ 3 -1]
[-14 5]
sage: Gamma0(7).are_equivalent_cusps(Cusp(1/3), Cusp(1/7))
False
Return a representation of this arithmetic subgroup in terms of the permutation action of SL2Z on the cosets of G.
At present this is only implemented for even subgroups.
EXAMPLE:
sage: Gamma0(3).as_permutation_group()
Arithmetic subgroup corresponding to permutations L=(2,3,4), R=(1,3,4)
Return coset representatives for self \ G, where G is another arithmetic subgroup that contains self. If G = None, default to G = SL2Z.
For generic arithmetic subgroups G this is carried out by Todd-Coxeter enumeration; here G is treated as a black box, implementing nothing but membership testing.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup().coset_reps()
...
NotImplementedError
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.coset_reps(Gamma0(3))
[[1 0]
[0 1], [ 0 -1]
[ 1 0], [ 0 -1]
[ 1 1], [ 0 -1]
[ 1 2]]
Return a triple (g, w, t) where g is an element of self generating the stabiliser of the given cusp, w is the width of the cusp, and t is 1 if the cusp is regular and -1 if not.
EXAMPLES:
sage: Gamma1(4).cusp_data(Cusps(1/2))
([ 1 -1] [ 4 -3], 1, -1)
Return the width of the orbit of cusps represented by c.
EXAMPLES:
sage: Gamma0(11).cusp_width(Cusps(oo))
1
sage: Gamma0(11).cusp_width(0)
11
sage: [Gamma0(100).cusp_width(c) for c in Gamma0(100).cusps()]
[100, 1, 4, 1, 1, 1, 4, 25, 1, 1, 4, 1, 25, 4, 1, 4, 1, 1]
Return a sorted list of inequivalent cusps for self, i.e. a set of
representatives for the orbits of self on 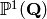 .
These should be returned in a reduced form where this makes sense.
.
These should be returned in a reduced form where this makes sense.
EXAMPLES:
sage: Gamma0(36).cusps()
[0, 1/18, 1/12, 1/9, 1/6, 1/4, 1/3, 5/12, 1/2, 2/3, 5/6, Infinity]
sage: Gamma0(36).cusps(algorithm='modsym') == Gamma0(36).cusps()
True
sage: GammaH(36, [19,29]).cusps() == Gamma0(36).cusps()
True
sage: Gamma0(1).cusps()
[Infinity]
Return the dimension of the space of weight k cusp forms for this group. This is given by a standard formula in terms of k and various invariants of the group; see Diamond + Shurman, “A First Course in Modular Forms”, section 3.5 and 3.6. If k is not given, default to k = 2.
For dimensions of spaces of cusp forms with character for Gamma1, use the standalone function dimension_cusp_forms().
For weight 1 cusp forms this function only works in cases where one can prove solely in terms of Riemann-Roch theory that there aren’t any cusp forms (i.e. when the number of regular cusps is strictly greater than the degree of the canonical divisor). Otherwise a NotImplementedError is raised.
EXAMPLE:
sage: Gamma1(31).dimension_cusp_forms(2)
26
sage: Gamma1(3).dimension_cusp_forms(1)
0
sage: Gamma1(4).dimension_cusp_forms(1) # irregular cusp
0
sage: Gamma1(31).dimension_cusp_forms(1)
...
NotImplementedError: Computation of dimensions of weight 1 cusp forms spaces not implemented in general
Return the dimension of the space of weight k Eisenstein series for this group, which is a subspace of the space of modular forms complementary to the space of cusp forms.
INPUT:
EXAMPLES:
sage: GammaH(33,[2]).dimension_eis()
7
sage: GammaH(33,[2]).dimension_eis(3)
0
sage: GammaH(33, [2,5]).dimension_eis(2)
3
sage: GammaH(33, [4]).dimension_eis(1)
4
Return the dimension of the space of weight k modular forms for this group. This is given by a standard formula in terms of k and various invariants of the group; see Diamond + Shurman, “A First Course in Modular Forms”, section 3.5 and 3.6. If k is not given, defaults to k = 2.
For dimensions of spaces of modular forms with character for Gamma1, use the standalone function dimension_modular_forms().
For weight 1 modular forms this function only works in cases where one can prove solely in terms of Riemann-Roch theory that there aren’t any cusp forms (i.e. when the number of regular cusps is strictly greater than the degree of the canonical divisor). Otherwise a NotImplementedError is raised.
EXAMPLE:
sage: Gamma1(31).dimension_modular_forms(2)
55
sage: Gamma1(3).dimension_modular_forms(1)
1
sage: Gamma1(4).dimension_modular_forms(1) # irregular cusp
1
sage: Gamma1(31).dimension_modular_forms(1)
...
NotImplementedError: Computation of dimensions of weight 1 cusp forms spaces not implemented in general
Return the i-th generator of self, i.e. the i-th element of the tuple self.gens().
EXAMPLES:
sage: SL2Z.gen(1)
[1 1]
[0 1]
Return the generalised level of self, i.e. the least common multiple of the widths of all cusps. Wohlfart’s theorem tells us that this is equal to the (conventional) level of self when self is a congruence subgroup.
EXAMPLE:
sage: Gamma0(18).generalised_level()
18
sage: sage.modular.arithgroup.congroup_generic.CongruenceSubgroup(5).index()
...
NotImplementedError
Return generators for this congruence subgroup.
This is carried out using an “inverse Todd-Coxeter” algorithm.
A Cython version of this for the special case of 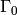 and
and 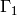 is
implemented in the function congroup_pyx.generators_helper. See the documentation
there for further details. Here we are assuming far less about the
group, so the computation is exceptionally slow!
is
implemented in the function congroup_pyx.generators_helper. See the documentation
there for further details. Here we are assuming far less about the
group, so the computation is exceptionally slow!
EXAMPLE:
sage: Gamma(2).generators()
[[1 2]
[0 1],
[-1 0]
[ 0 -1],
[-1 0]
[ 0 -1],
[ 1 0]
[-2 1],
[-1 2]
[-2 3],
[-1 0]
[ 2 -1],
[1 0]
[2 1]]
Return a tuple of generators for this congruence subgroup.
The generators need not be minimal.
EXAMPLES:
sage: SL2Z.gens()
([ 0 -1]
[ 1 0], [1 1]
[0 1])
Return the genus of the modular curve of self.
EXAMPLES:
sage: Gamma1(5).genus()
0
sage: Gamma1(31).genus()
26
sage: Gamma1(157).genus() == dimension_cusp_forms(Gamma1(157), 2)
True
sage: GammaH(7, [2]).genus()
0
sage: [Gamma0(n).genus() for n in [1..23]]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 2, 2]
sage: [n for n in [1..200] if Gamma0(n).genus() == 1]
[11, 14, 15, 17, 19, 20, 21, 24, 27, 32, 36, 49]
Return the index of self in the full modular group.
EXAMPLES:
sage: Gamma0(17).index()
18
sage: sage.modular.arithgroup.congroup_generic.CongruenceSubgroup(5).index()
...
NotImplementedError
Return True if this arithmetic subgroup is abelian.
Since arithmetic subgroups are always nonabelian, this always returns False.
EXAMPLES:
sage: SL2Z.is_abelian()
False
sage: Gamma0(3).is_abelian()
False
sage: Gamma1(12).is_abelian()
False
sage: GammaH(4, [3]).is_abelian()
False
Return True if self is a congruence subgroup.
EXAMPLE:
sage: Gamma0(5).is_congruence()
True
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup().is_congruence()
...
NotImplementedError
Return True precisely if this subgroup contains the matrix -1.
EXAMPLES:
sage: SL2Z.is_even()
True
sage: Gamma0(20).is_even()
True
sage: Gamma1(5).is_even()
False
sage: GammaH(11, [3]).is_even()
False
Return True if this arithmetic subgroup is finite.
Since arithmetic subgroups are always infinite, this always returns False.
EXAMPLES:
sage: SL2Z.is_finite()
False
sage: Gamma0(3).is_finite()
False
sage: Gamma1(12).is_finite()
False
sage: GammaH(4, [3]).is_finite()
False
Return True precisely if this subgroup is a normal subgroup of SL2Z.
EXAMPLES:
sage: Gamma(3).is_normal()
True
sage: Gamma1(3).is_normal()
False
Return True precisely if this subgroup does not contain the matrix -1.
EXAMPLES:
sage: SL2Z.is_odd()
False
sage: Gamma0(20).is_odd()
False
sage: Gamma1(5).is_odd()
True
sage: GammaH(11, [3]).is_odd()
True
Return True if the orbit of the given cusp is a regular cusp for self, otherwise False. This is automatically true if -1 is in self.
EXAMPLES:
sage: Gamma1(4).is_regular_cusp(Cusps(1/2))
False
sage: Gamma1(4).is_regular_cusp(Cusps(oo))
True
Return True if self is a subgroup of right, and False otherwise. For generic arithmetic subgroups this is done by the absurdly slow algorithm of checking all of the generators of self to see if they are in right.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup().is_subgroup(SL2Z)
...
NotImplementedError
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.is_subgroup(Gamma1(18), Gamma0(6))
True
Return the number of cusps of this arithmetic subgroup. This is provided as a separate function since for dimension formulae in even weight all we need to know is the number of cusps, and this can be calculated very quickly, while enumerating all cusps is much slower.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.ncusps(Gamma0(7))
2
Return the number of generators for this arithmetic subgroup.
This need not be the minimal number of generators of self.
EXAMPLES:
sage: Gamma0(22).ngens()
42
sage: Gamma1(14).ngens()
219
sage: GammaH(11, [3]).ngens()
31
sage: SL2Z.ngens()
2
Return the number of cusps of self that are “irregular”, i.e. their stabiliser can only be generated by elements with both eigenvalues -1 rather than +1. If the group contains -1, every cusp is clearly regular.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.nirregcusps(Gamma1(4))
1
Return the number of cusps of self that are “regular”, i.e. their stabiliser has a generator with both eigenvalues +1 rather than -1. If the group contains -1, every cusp is clearly regular.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.nregcusps(Gamma1(4))
2
Return the number of orbits of elliptic points of order 2 for this arithmetic subgroup.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup().nu2()
...
NotImplementedError
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.nu2(Gamma0(1105)) == 8
True
Return the number of orbits of elliptic points of order 3 for this arithmetic subgroup.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup().nu3()
...
NotImplementedError
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.nu3(Gamma0(1729)) == 8
True
We test that a bug in handling of subgroups not containing -1 is fixed:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup.nu3(GammaH(7, [2]))
2
Return the number of elements in this arithmetic subgroup.
Since arithmetic subgroups are always infinite, this always returns infinity.
EXAMPLES:
sage: SL2Z.order()
+Infinity
sage: Gamma0(5).order()
+Infinity
sage: Gamma1(2).order()
+Infinity
sage: GammaH(12, [5]).order()
+Infinity
Return the index of the image of self in 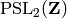 . This is equal
to the index of self if self contains -1, and half of this otherwise.
. This is equal
to the index of self if self contains -1, and half of this otherwise.
This is equal to the degree of the natural map from the modular curve
of self to the  -line.
-line.
EXAMPLE:
sage: Gamma0(5).projective_index()
6
sage: Gamma1(5).projective_index()
12
Given a cusp 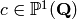 , return the
unique reduced cusp equivalent to c under the action of self,
where a reduced cusp is an element
, return the
unique reduced cusp equivalent to c under the action of self,
where a reduced cusp is an element  with r,s coprime
integers, s as small as possible, and r as small as possible
for that s.
with r,s coprime
integers, s as small as possible, and r as small as possible
for that s.
NOTE: This function should be overridden by all subclasses.
EXAMPLES:
sage: sage.modular.arithgroup.arithgroup_generic.ArithmeticSubgroup().reduce_cusp(1/4)
...
NotImplementedError
Compute coset representatives for self \ G via Todd-Coxeter enumeration. If G = None, default to G = SL2Z. Also computes generators for G at the same time. Return value is a tuple (list of coset reps, list of generators).
This is extremely slow in general.
EXAMPLE:
sage: Gamma0(3).todd_coxeter() ([[1 0] [0 1], [ 0 -1] [ 1 0], [ 0 -1] [ 1 1], [ 0 -1] [ 1 2]], [[1 1] [0 1], [-1 0] [ 0 -1], [ 1 0] [-3 1], [-2 -1] [ 3 1], [-1 -1] [ 3 2]])
Return True if x is of type ArithmeticSubgroup.
EXAMPLE:
sage: from sage.modular.arithgroup.all import is_ArithmeticSubgroup
sage: is_ArithmeticSubgroup(GL(2, GF(7)))
False
sage: is_ArithmeticSubgroup(Gamma0(4))
True