TESTS:
sage: m = matrix(ZZ['x'], 2, 3, [1..6])
sage: TestSuite(m).run()
Bases: sage.matrix.matrix1.Matrix
Returns the adjoint matrix of self (matrix of cofactors).
OUTPUT:
ALGORITHM:
Use PARI whenever the method self._adjoint is included to do so in an inheriting class. Otherwise, use a generic division-free algorithm to compute the characteristic polynomial and hence the adjoint.
The result is cached.
EXAMPLES:
sage: M = Matrix(ZZ,2,2,[5,2,3,4]) ; M
[5 2]
[3 4]
sage: N = M.adjoint() ; N
[ 4 -2]
[-3 5]
sage: M * N
[14 0]
[ 0 14]
sage: N * M
[14 0]
[ 0 14]
sage: M = Matrix(QQ,2,2,[5/3,2/56,33/13,41/10]) ; M
[ 5/3 1/28]
[33/13 41/10]
sage: N = M.adjoint() ; N
[ 41/10 -1/28]
[-33/13 5/3]
sage: M * N
[7363/1092 0]
[ 0 7363/1092]
AUTHORS:
Returns the current matrix as a sum of permutation matrices
According to the Birkhoff-von Neumann Theorem, any bistochastic matrix can be written as a positive sum of permutation matrices, which also means that the polytope of bistochastic matrices is integer.
As a non-bistochastic matrix can obviously not be written as a sum of permutations, this theorem is an equivalence.
This function, given a bistochastic matrix, returns the corresponding decomposition.
EXAMPLE:
We create a bistochastic matrix from a convex sum of permutations, then try to deduce the decomposition from the matrix
sage: L = []
sage: L.append((9,Permutation([4, 1, 3, 5, 2])))
sage: L.append((6,Permutation([5, 3, 4, 1, 2])))
sage: L.append((3,Permutation([3, 1, 4, 2, 5])))
sage: L.append((2,Permutation([1, 4, 2, 3, 5])))
sage: M = sum([c * p.to_matrix() for (c,p) in L])
sage: decomp = sage.combinat.permutation.bistochastic_as_sum_of_permutations(M)
sage: print decomp
2*B[[1, 4, 2, 3, 5]] + 3*B[[3, 1, 4, 2, 5]] + 9*B[[4, 1, 3, 5, 2]] + 6*B[[5, 3, 4, 1, 2]]
An exception is raised when the matrix is not bistochastic:
sage: M = Matrix([[2,3],[2,2]])
sage: decomp = sage.combinat.permutation.bistochastic_as_sum_of_permutations(M)
...
ValueError: The matrix is not bistochastic
Synonym for self.charpoly(...).
EXAMPLES:
sage: a = matrix(QQ, 2,2, [1,2,3,4]); a
[1 2]
[3 4]
sage: a.characteristic_polynomial('T')
T^2 - 5*T - 2
Returns the characteristic polynomial of self, as a polynomial over the base ring.
ALGORITHM:
In the generic case of matrices over a ring (commutative and with
unity), there is a division-free algorithm, which can be accessed
using "df", with complexity 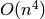 . Alternatively, by
specifying "hessenberg", this method computes the Hessenberg
form of the matrix and then reads off the characteristic polynomial.
Moreover, for matrices over number fields, this method can use
PARI’s charpoly implementation instead.
. Alternatively, by
specifying "hessenberg", this method computes the Hessenberg
form of the matrix and then reads off the characteristic polynomial.
Moreover, for matrices over number fields, this method can use
PARI’s charpoly implementation instead.
The method’s logic is as follows: If no algorithm is specified, first check if the base ring is a number field (and then use PARI), otherwise check if the base ring is the ring of integers modulo n (in which case compute the characteristic polynomial of a lift of the matrix to the integers, and then coerce back to the base), next check if the base ring is an exact field (and then use the Hessenberg form), or otherwise, use the generic division-free algorithm. If an algorithm is specified explicitly, if algorithm == "hessenberg", use the Hessenberg form, or otherwise use the generic division-free algorithm.
The result is cached.
INPUT:
var - a variable name (default: ‘x’)
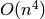 division-free algorithm
division-free algorithmEXAMPLES:
First a matrix over  :
:
sage: A = MatrixSpace(ZZ,2)( [1,2, 3,4] )
sage: f = A.charpoly('x')
sage: f
x^2 - 5*x - 2
sage: f.parent()
Univariate Polynomial Ring in x over Integer Ring
sage: f(A)
[0 0]
[0 0]
An example over  :
:
sage: A = MatrixSpace(QQ,3)(range(9))
sage: A.charpoly('x')
x^3 - 12*x^2 - 18*x
sage: A.trace()
12
sage: A.determinant()
0
We compute the characteristic polynomial of a matrix over the
polynomial ring ![\ZZ[a]](../../_images/math/c60a1a232148ace41b1216138bdbbdb392cf96b4.png) :
:
sage: R.<a> = PolynomialRing(ZZ)
sage: M = MatrixSpace(R,2)([a,1, a,a+1]); M
[ a 1]
[ a a + 1]
sage: f = M.charpoly('x'); f
x^2 + (-2*a - 1)*x + a^2
sage: f.parent()
Univariate Polynomial Ring in x over Univariate Polynomial Ring in a over Integer Ring
sage: M.trace()
2*a + 1
sage: M.determinant()
a^2
We compute the characteristic polynomial of a matrix over the
multi-variate polynomial ring ![\ZZ[x,y]](../../_images/math/5b267881d8ba398c55b2317cd9d9db277c50cd4a.png) :
:
sage: R.<x,y> = PolynomialRing(ZZ,2)
sage: A = MatrixSpace(R,2)([x, y, x^2, y^2])
sage: f = A.charpoly('x'); f
x^2 + (-y^2 - x)*x - x^2*y + x*y^2
It’s a little difficult to distinguish the variables. To fix this,
we temporarily view the indeterminate as 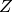 :
:
sage: with localvars(f.parent(), 'Z'): print f
Z^2 + (-y^2 - x)*Z - x^2*y + x*y^2
We could also compute f in terms of Z from the start:
sage: A.charpoly('Z')
Z^2 + (-y^2 - x)*Z - x^2*y + x*y^2
Here is an example over a number field:
sage: x = QQ['x'].gen()
sage: K.<a> = NumberField(x^2 - 2)
sage: m = matrix(K, [[a-1, 2], [a, a+1]])
sage: m.charpoly('Z')
Z^2 - 2*a*Z - 2*a + 1
sage: m.charpoly('a')(m) == 0
True
Here is an example over a general commutative ring, that is to say, as of version 4.0.2, SAGE does not even positively determine that S in the following example is an integral domain. But the computation of the characteristic polynomial succeeds as follows:
sage: R.<a,b> = QQ[]
sage: S.<x,y> = R.quo((b^3))
sage: A = matrix(S, [[x*y^2,2*x],[2,x^10*y]])
sage: A
[ x*y^2 2*x]
[ 2 x^10*y]
sage: A.charpoly('T')
T^2 + (-x^10*y - x*y^2)*T - 4*x
TESTS:
sage: P.<a,b,c> = PolynomialRing(Rationals())
sage: u = MatrixSpace(P,3)([[0,0,a],[1,0,b],[0,1,c]])
sage: Q.<x> = PolynomialRing(P)
sage: u.charpoly('x')
x^3 - c*x^2 - b*x - a
AUTHORS:
Return the Cholesky decomposition of self.
The computed decomposition is cached and returned on subsequent calls. Methods such as solve_left() may also take advantage of the cached decomposition depending on the exact implementation.
INPUT:
The input matrix must be:
If not, a ValueError exception will be raised.
OUTPUT:
An immutable lower triangular matrix  such that
such that 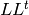 equals self.
equals self.
ALGORITHM:
Calls the method _cholesky_decomposition_, which by default uses a standard recursion.
Warning
This implementation uses a standard recursion that is not known to be numerically stable.
Warning
It is potentially expensive to ensure that the input is positive definite. Therefore this is not checked and it is possible that the output matrix is not a valid Cholesky decomposition of self. An example of this is given in the tests below.
EXAMPLES:
Here is an example over the real double field; internally, this uses SciPy:
sage: r = matrix(RDF, 5, 5, [ 0,0,0,0,1, 1,1,1,1,1, 16,8,4,2,1, 81,27,9,3,1, 256,64,16,4,1 ])
sage: m = r * r.transpose(); m
[ 1.0 1.0 1.0 1.0 1.0]
[ 1.0 5.0 31.0 121.0 341.0]
[ 1.0 31.0 341.0 1555.0 4681.0]
[ 1.0 121.0 1555.0 7381.0 22621.0]
[ 1.0 341.0 4681.0 22621.0 69905.0]
sage: L = m.cholesky_decomposition(); L
[ 1.0 0.0 0.0 0.0 0.0]
[ 1.0 2.0 0.0 0.0 0.0]
[ 1.0 15.0 10.7238052948 0.0 0.0]
[ 1.0 60.0 60.9858144589 7.79297342371 0.0]
[ 1.0 170.0 198.623524155 39.3665667796 1.72309958068]
sage: L.parent()
Full MatrixSpace of 5 by 5 dense matrices over Real Double Field
sage: L*L.transpose()
[ 1.0 1.0 1.0 1.0 1.0]
[ 1.0 5.0 31.0 121.0 341.0]
[ 1.0 31.0 341.0 1555.0 4681.0]
[ 1.0 121.0 1555.0 7381.0 22621.0]
[ 1.0 341.0 4681.0 22621.0 69905.0]
sage: ( L*L.transpose() - m ).norm(1) < 2^-30
True
The result is immutable:
sage: L[0,0] = 0
Traceback (most recent call last):
...
ValueError: matrix is immutable; please change a copy instead (i.e., use copy(M) to change a copy of M).
Here is an example over a higher precision real field:
sage: r = matrix(RealField(100), 5, 5, [ 0,0,0,0,1, 1,1,1,1,1, 16,8,4,2,1, 81,27,9,3,1, 256,64,16,4,1 ])
sage: m = r * r.transpose()
sage: L = m.cholesky_decomposition()
sage: L.parent()
Full MatrixSpace of 5 by 5 dense matrices over Real Field with 100 bits of precision
sage: ( L*L.transpose() - m ).norm(1) < 2^-50
True
Here is a Hermitian example:
sage: r = matrix(CDF, 2, 2, [ 1, -2*I, 2*I, 6 ]); r
[ 1.0 -2.0*I]
[ 2.0*I 6.0]
sage: r.eigenvalues()
[0.298437881284, 6.70156211872]
sage: ( r - r.conjugate().transpose() ).norm(1) < 1e-30
True
sage: L = r.cholesky_decomposition(); L
[ 1.0 0]
[ 2.0*I 1.41421356237]
sage: ( r - L*L.conjugate().transpose() ).norm(1) < 1e-30
True
sage: L.parent()
Full MatrixSpace of 2 by 2 dense matrices over Complex Double Field
TESTS:
The following examples are not positive definite:
sage: m = -identity_matrix(3).change_ring(RDF)
sage: m.cholesky_decomposition()
...
ValueError: The input matrix was not symmetric and positive definite
sage: m = -identity_matrix(2).change_ring(RealField(100))
sage: m.cholesky_decomposition()
...
ValueError: The input matrix was not symmetric and positive definite
Here is a large example over a higher precision complex field:
sage: r = MatrixSpace(ComplexField(100), 6, 6).random_element()
sage: m = r * r.conjugate().transpose()
sage: m.change_ring(CDF) # for display purposes
[ 2.5891918451 1.58308081508 - 0.93917354232*I 0.4508660242 - 0.898986215453*I -0.125366701515 - 1.32575360944*I -0.161174433016 - 1.92791089094*I -0.852634739628 + 0.592301526741*I]
[ 1.58308081508 + 0.93917354232*I 3.39096359127 -0.823614467666 - 0.70698381556*I 0.964188058124 - 1.80624774667*I 0.884237835922 - 1.12339941545*I -1.14625014365 + 0.64233624728*I]
[ 0.4508660242 + 0.898986215453*I -0.823614467666 + 0.70698381556*I 4.94253304499 -1.61505575668 - 0.539043412246*I 1.16580777654 - 2.24511228411*I 1.22264068801 + 1.21537124374*I]
[ -0.125366701515 + 1.32575360944*I 0.964188058124 + 1.80624774667*I -1.61505575668 + 0.539043412246*I 3.73381314119 0.30433428398 + 0.852908810051*I -3.03684690541 - 0.437547321546*I]
[ -0.161174433016 + 1.92791089094*I 0.884237835922 + 1.12339941545*I 1.16580777654 + 2.24511228411*I 0.30433428398 - 0.852908810051*I 4.24526168246 -1.03348617777 - 0.0868365809834*I]
[-0.852634739628 - 0.592301526741*I -1.14625014365 - 0.64233624728*I 1.22264068801 - 1.21537124374*I -3.03684690541 + 0.437547321546*I -1.03348617777 + 0.0868365809834*I 3.95129528414]
sage: eigs = m.change_ring(CDF).eigenvalues() # again for display purposes
sage: all(imag(e) < 1e-15 for e in eigs)
True
sage: [real(e) for e in eigs]
[10.463115298, 7.42365754809, 3.36964641458, 1.25904669699, 0.00689184179485, 0.330700789655]
sage: ( m - m.conjugate().transpose() ).norm(1) < 1e-50
True
sage: L = m.cholesky_decomposition(); L.change_ring(CDF)
[ 1.60909659284 0 0 0 0 0]
[ 0.98383205963 + 0.583665111527*I 1.44304300258 0 0 0 0]
[ 0.280198234342 + 0.558690024857*I -0.987753204014 + 0.222355529831*I 1.87797472744 0 0 0]
[-0.0779112342122 + 0.823911762252*I 0.388034921026 + 0.658457765816*I -0.967353506777 + 0.533197825056*I 1.11566210466 0 0]
[ -0.100164548065 + 1.19813247975*I 0.196442380181 - 0.0788779556296*I 0.391945946049 + 0.968705709652*I -0.763918835279 + 0.415837754312*I 0.952045463612 0]
[ -0.529884124682 - 0.368095693804*I -0.284183173327 - 0.408488713349*I 0.738503847 - 0.998388403822*I -1.02976885437 - 0.563208016935*I -0.521713761022 - 0.245786008887*I 0.187109707194]
sage: ( m - L*L.conjugate().transpose() ).norm(1) < 1e-20
True
sage: L.parent()
Full MatrixSpace of 6 by 6 dense matrices over Complex Field with 100 bits of precision
sage: L[0,0] = 0
Traceback (most recent call last):
...
ValueError: matrix is immutable; please change a copy instead (i.e., use copy(M) to change a copy of M).
Here is an example that returns an incorrect answer, because the input is not positive definite:
sage: r = matrix(CDF, 2, 2, [ 1, -2*I, 2*I, 0 ]); r
[ 1.0 -2.0*I]
[ 2.0*I 0]
sage: r.eigenvalues()
[2.56155281281, -1.56155281281]
sage: ( r - r.conjugate().transpose() ).norm(1) < 1e-30
True
sage: L = r.cholesky_decomposition(); L
[ 1.0 0]
[2.0*I 2.0*I]
sage: L*L.conjugate().transpose()
[ 1.0 -2.0*I]
[ 2.0*I 8.0]
Return the free module over the base ring spanned by the columns of this matrix.
EXAMPLES:
sage: t = matrix(QQ, 3, range(9)); t
[0 1 2]
[3 4 5]
[6 7 8]
sage: t.column_module()
Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[ 1 0 -1]
[ 0 1 2]
Return the vector space over the base ring spanned by the columns of this matrix.
EXAMPLES:
sage: M = MatrixSpace(QQ,3,3)
sage: A = M([1,9,-7,4/5,4,3,6,4,3])
sage: A.column_space()
Vector space of degree 3 and dimension 3 over Rational Field
Basis matrix:
[1 0 0]
[0 1 0]
[0 0 1]
sage: W = MatrixSpace(CC,2,2)
sage: B = W([1, 2+3*I,4+5*I,9]); B
[ 1.00000000000000 2.00000000000000 + 3.00000000000000*I]
[4.00000000000000 + 5.00000000000000*I 9.00000000000000]
sage: B.column_space()
Vector space of degree 2 and dimension 2 over Complex Field with 53 bits of precision
Basis matrix:
[1.00000000000000 0]
[ 0 1.00000000000000]
Return the conjugate of self, i.e. the matrix whose entries are the conjugates of the entries of self.
EXAMPLES:
sage: A = matrix(CDF, [[1+I,1],[0,2*I]])
sage: A.conjugate()
[1.0 - 1.0*I 1.0]
[ 0 -2.0*I]
A matrix over a not-totally-real number field:
sage: K.<j> = NumberField(x^2+5)
sage: M = matrix(K, [[1+j,1], [0,2*j]])
sage: M.conjugate()
[-j + 1 1]
[ 0 -2*j]
Conjugates work (trivially) for matrices over rings that embed canonically into the real numbers:
sage: M = random_matrix(ZZ, 2)
sage: M == M.conjugate()
True
sage: M = random_matrix(QQ, 3)
sage: M == M.conjugate()
True
sage: M = random_matrix(RR, 2)
sage: M == M.conjugate()
True
Returns the decomposition of the free module on which this matrix A acts from the right (i.e., the action is x goes to x A), along with whether this matrix acts irreducibly on each factor. The factors are guaranteed to be sorted in the same way as the corresponding factors of the characteristic polynomial.
Let A be the matrix acting from the on the vector space V of column
vectors. Assume that A is square. This function computes maximal
subspaces W_1, ..., W_n corresponding to Galois conjugacy classes
of eigenvalues of A. More precisely, let 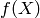 be the characteristic
polynomial of A. This function computes the subspace
be the characteristic
polynomial of A. This function computes the subspace
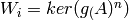 , where
, where 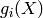 is an irreducible
factor of
is an irreducible
factor of 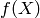 and
and 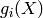 exactly divides
exactly divides 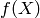 . If the optional
parameter is_diagonalizable is True, then we let
. If the optional
parameter is_diagonalizable is True, then we let 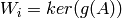 ,
since then we know that
,
since then we know that 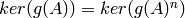 .
.
INPUT:
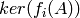 for each factor
for each factor  .
.Note
If the base ring is not a field, the kernel algorithm is used.
OUTPUT:
EXAMPLES:
sage: A = matrix(ZZ, 4, [3,4,5,6,7,3,8,10,14,5,6,7,2,2,10,9])
sage: B = matrix(QQ, 6, range(36))
sage: B*11
[ 0 11 22 33 44 55]
[ 66 77 88 99 110 121]
[132 143 154 165 176 187]
[198 209 220 231 242 253]
[264 275 286 297 308 319]
[330 341 352 363 374 385]
sage: A.decomposition()
[
(Ambient free module of rank 4 over the principal ideal domain Integer Ring, True)
]
sage: B.decomposition()
[
(Vector space of degree 6 and dimension 2 over Rational Field
Basis matrix:
[ 1 0 -1 -2 -3 -4]
[ 0 1 2 3 4 5], True),
(Vector space of degree 6 and dimension 4 over Rational Field
Basis matrix:
[ 1 0 0 0 -5 4]
[ 0 1 0 0 -4 3]
[ 0 0 1 0 -3 2]
[ 0 0 0 1 -2 1], False)
]
Suppose the right action of self on M leaves M invariant. Return the decomposition of M as a list of pairs (W, is_irred) where is_irred is True if the charpoly of self acting on the factor W is irreducible.
Additional inputs besides M are passed onto the decomposition command.
EXAMPLES:
sage: t = matrix(QQ, 3, [3, 0, -2, 0, -2, 0, 0, 0, 0]); t
[ 3 0 -2]
[ 0 -2 0]
[ 0 0 0]
sage: t.fcp('X') # factored charpoly
(X - 3) * X * (X + 2)
sage: v = kernel(t*(t+2)); v # an invariant subspace
Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[0 1 0]
[0 0 1]
sage: D = t.decomposition_of_subspace(v); D
[
(Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[0 0 1], True),
(Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[0 1 0], True)
]
sage: t.restrict(D[0][0])
[0]
sage: t.restrict(D[1][0])
[-2]
We do a decomposition over ZZ:
sage: a = matrix(ZZ,6,[0, 0, -2, 0, 2, 0, 2, -4, -2, 0, 2, 0, 0, 0, -2, -2, 0, 0, 2, 0, -2, -4, 2, -2, 0, 2, 0, -2, -2, 0, 0, 2, 0, -2, 0, 0])
sage: a.decomposition_of_subspace(ZZ^6)
[
(Free module of degree 6 and rank 2 over Integer Ring
Echelon basis matrix:
[ 1 0 1 -1 1 -1]
[ 0 1 0 -1 2 -1], False),
(Free module of degree 6 and rank 4 over Integer Ring
Echelon basis matrix:
[ 1 0 -1 0 1 0]
[ 0 1 0 0 0 0]
[ 0 0 0 1 0 0]
[ 0 0 0 0 0 1], False)
]
Return the least common multiple of the denominators of the elements of self.
If there is no denominator function for the base field, or no LCM function for the denominators, raise a TypeError.
EXAMPLES:
sage: A = MatrixSpace(QQ,2)(['1/2', '1/3', '1/5', '1/7'])
sage: A.denominator()
210
A trivial example:
sage: A = matrix(QQ, 0,2)
sage: A.denominator()
1
Denominators are not defined for real numbers:
sage: A = MatrixSpace(RealField(),2)([1,2,3,4])
sage: A.denominator()
...
TypeError: denominator not defined for elements of the base ring
We can even compute the denominator of matrix over the fraction
field of ![\ZZ[x]](../../_images/math/997bd738c8f73a5487d82a0af9f18a75a09c06ec.png) .
.
sage: K.<x> = Frac(ZZ['x'])
sage: A = MatrixSpace(K,2)([1/x, 2/(x+1), 1, 5/(x^3)])
sage: A.denominator()
x^4 + x^3
Here’s an example involving a cyclotomic field:
sage: K.<z> = CyclotomicField(3)
sage: M = MatrixSpace(K,3,sparse=True)
sage: A = M([(1+z)/3,(2+z)/3,z/3,1,1+z,-2,1,5,-1+z])
sage: print A
[1/3*z + 1/3 1/3*z + 2/3 1/3*z]
[ 1 z + 1 -2]
[ 1 5 z - 1]
sage: print A.denominator()
3
Return the density of self.
By density we understand the ration of the number of nonzero positions and the self.nrows() * self.ncols(), i.e. the number of possible nonzero positions.
EXAMPLE:
First, note that the density parameter does not ensure the density of a matrix, it is only an upper bound.
sage: A = random_matrix(GF(127),200,200,density=0.3)
sage: A.density()
5211/20000
sage: A = matrix(QQ,3,3,[0,1,2,3,0,0,6,7,8])
sage: A.density()
2/3
sage: a = matrix([[],[],[],[]])
sage: a.density()
0
Derivative with respect to variables supplied in args.
Multiple variables and iteration counts may be supplied; see documentation for the global derivative() function for more details.
EXAMPLES:
sage: v = vector([1,x,x^2])
sage: v.derivative(x)
(0, 1, 2*x)
sage: type(v.derivative(x)) == type(v)
True
sage: v = vector([1,x,x^2], sparse=True)
sage: v.derivative(x)
(0, 1, 2*x)
sage: type(v.derivative(x)) == type(v)
True
sage: v.derivative(x,x)
(0, 0, 2)
Synonym for self.determinant(...).
EXAMPLES:
sage: A = MatrixSpace(Integers(8),3)([1,7,3, 1,1,1, 3,4,5])
sage: A.det()
6
Returns the determinant of self.
ALGORITHM:
For small matrices (n less than 4), this is computed using the naive formula. In the specific case of matrices over the integers modulo a non-prime, the determinant of a lift is computed over the integers. In general, the characteristic polynomial is computed either using the Hessenberg form (specified by "hessenberg") or the generic division-free algorithm (specified by "df"). When the base ring is an exact field, the default choice is "hessenberg", otherwise it is "df". Note that for matrices over most rings, more sophisticated algorithms can be used. (Type A.determinant? to see what is done for a specific matrix A.)
INPUT:
EXAMPLES:
sage: A = MatrixSpace(Integers(8),3)([1,7,3, 1,1,1, 3,4,5])
sage: A.determinant()
6
sage: A.determinant() is A.determinant()
True
sage: A[0,0] = 10
sage: A.determinant()
7
We compute the determinant of the arbitrary 3x3 matrix:
sage: R = PolynomialRing(QQ,9,'x')
sage: A = matrix(R,3,R.gens())
sage: A
[x0 x1 x2]
[x3 x4 x5]
[x6 x7 x8]
sage: A.determinant()
-x2*x4*x6 + x1*x5*x6 + x2*x3*x7 - x0*x5*x7 - x1*x3*x8 + x0*x4*x8
We create a matrix over ![\ZZ[x,y]](../../_images/math/5b267881d8ba398c55b2317cd9d9db277c50cd4a.png) and compute its
determinant.
and compute its
determinant.
sage: R.<x,y> = PolynomialRing(IntegerRing(),2)
sage: A = MatrixSpace(R,2)([x, y, x**2, y**2])
sage: A.determinant()
-x^2*y + x*y^2
TEST:
sage: A = matrix(5, 5, [next_prime(i^2) for i in range(25)])
sage: B = MatrixSpace(ZZ['x'], 5, 5)(A)
sage: A.det() - B.det()
0
We verify that trac 5569 is resolved (otherwise the following will hang for hours):
sage: d = random_matrix(GF(next_prime(10^20)),50).det()
sage: d = random_matrix(Integers(10^50),50).det()
AUTHORS:
- Unknown: No author specified in the file from 2009-06-25
- Sebastian Pancratz (2009-06-25): Use the division-free algorithm for charpoly
Return the echelon form of self.
Note
This row reduction does not use division if the matrix is not over a field (e.g., if the matrix is over the integers). If you want to calculate the echelon form using division, then use rref(), which assumes that the matrix entries are in a field (specifically, the field of fractions of the base ring of the matrix).
INPUT:
OUTPUT:
EXAMPLES:
sage: MS = MatrixSpace(GF(19),2,3)
sage: C = MS.matrix([1,2,3,4,5,6])
sage: C.rank()
2
sage: C.nullity()
0
sage: C.echelon_form()
[ 1 0 18]
[ 0 1 2]
Transform self into a matrix in echelon form over the same base ring as self.
INPUT:
EXAMPLES:
sage: a = matrix(QQ,3,range(9)); a
[0 1 2]
[3 4 5]
[6 7 8]
sage: a.echelonize()
sage: a
[ 1 0 -1]
[ 0 1 2]
[ 0 0 0]
An immutable matrix cannot be transformed into echelon form. Use self.echelon_form() instead:
sage: a = matrix(QQ,3,range(9)); a.set_immutable()
sage: a.echelonize()
...
ValueError: matrix is immutable; please change a copy instead (i.e., use copy(M) to change a copy of M).
sage: a.echelon_form()
[ 1 0 -1]
[ 0 1 2]
[ 0 0 0]
Echelon form over the integers is what is also classically often known as Hermite normal form:
sage: a = matrix(ZZ,3,range(9))
sage: a.echelonize(); a
[ 3 0 -3]
[ 0 1 2]
[ 0 0 0]
We compute an echelon form both over a domain and fraction field:
sage: R.<x,y> = QQ[]
sage: a = matrix(R, 2, [x,y,x,y])
sage: a.echelon_form() # not very useful? -- why two copies of the same row?
[x y]
[x y]
sage: b = a.change_ring(R.fraction_field())
sage: b.echelon_form() # potentially useful
[ 1 y/x]
[ 0 0]
Echelon form is not defined over arbitrary rings:
sage: a = matrix(Integers(9),3,range(9))
sage: a.echelon_form()
...
NotImplementedError: Echelon form not implemented over 'Ring of integers modulo 9'.
Involving a sparse matrix:
sage: m = matrix(3,[1, 1, 1, 1, 0, 2, 1, 2, 0], sparse=True); m
[1 1 1]
[1 0 2]
[1 2 0]
sage: m.echelon_form()
[ 1 0 2]
[ 0 1 -1]
[ 0 0 0]
sage: m.echelonize(); m
[ 1 0 2]
[ 0 1 -1]
[ 0 0 0]
Return matrices D and P, where D is a diagonal matrix of eigenvalues and P is the corresponding matrix where the rows are corresponding eigenvectors (or zero vectors) so that P*self = D*P.
EXAMPLES:
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: D, P = A.eigenmatrix_left()
sage: D
[ 0 0 0]
[ 0 -1.348469228349535? 0]
[ 0 0 13.34846922834954?]
sage: P
[ 1 -2 1]
[ 1 0.3101020514433644? -0.3797958971132713?]
[ 1 1.289897948556636? 1.579795897113272?]
sage: P*A == D*P
True
Because P is invertible, A is diagonalizable.
sage: A == (~P)*D*P
True
The matrix P may contain zero rows corresponding to eigenvalues for which the algebraic multiplicity is greater than the geometric multiplicity. In these cases, the matrix is not diagonalizable.
sage: A = jordan_block(2,3); A
[2 1 0]
[0 2 1]
[0 0 2]
sage: A = jordan_block(2,3)
sage: D, P = A.eigenmatrix_left()
sage: D
[2 0 0]
[0 2 0]
[0 0 2]
sage: P
[0 0 1]
[0 0 0]
[0 0 0]
sage: P*A == D*P
True
Return matrices D and P, where D is a diagonal matrix of eigenvalues and P is the corresponding matrix where the columns are corresponding eigenvectors (or zero vectors) so that self*P = P*D.
EXAMPLES:
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: D, P = A.eigenmatrix_right()
sage: D
[ 0 0 0]
[ 0 -1.348469228349535? 0]
[ 0 0 13.34846922834954?]
sage: P
[ 1 1 1]
[ -2 0.1303061543300932? 3.069693845669907?]
[ 1 -0.7393876913398137? 5.139387691339814?]
sage: A*P == P*D
True
Because P is invertible, A is diagonalizable.
sage: A == P*D*(~P)
True
The matrix P may contain zero columns corresponding to eigenvalues for which the algebraic multiplicity is greater than the geometric multiplicity. In these cases, the matrix is not diagonalizable.
sage: A = jordan_block(2,3); A
[2 1 0]
[0 2 1]
[0 0 2]
sage: A = jordan_block(2,3)
sage: D, P = A.eigenmatrix_right()
sage: D
[2 0 0]
[0 2 0]
[0 0 2]
sage: P
[1 0 0]
[0 0 0]
[0 0 0]
sage: A*P == P*D
True
Compute left eigenspaces of a matrix.
If algebraic_multiplicity=False, return a list of pairs (e, V) where e runs through all eigenvalues (up to Galois conjugation) of this matrix, and V is the corresponding left eigenspace.
If algebraic_multiplicity=True, return a list of pairs (e, V, n) where e and V are as above and n is the algebraic multiplicity of the eigenvalue. If the eigenvalues are given symbolically, as roots of an irreducible factor of the characteristic polynomial, then the algebraic multiplicity returned is the multiplicity of each conjugate eigenvalue.
The eigenspaces are returned sorted by the corresponding characteristic polynomials, where polynomials are sorted in dictionary order starting with constant terms.
INPUT:
Warning
Uses a somewhat naive algorithm (simply factors the characteristic polynomial and computes kernels directly over the extension field).
TODO:
Maybe implement the better algorithm that is in dual_eigenvector in sage/modular/hecke/module.py.
EXAMPLES: We compute the left eigenspaces of a  rational matrix.
rational matrix.
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: es = A.eigenspaces_left(); es
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1]),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/15*a1 + 2/5 2/15*a1 - 1/5])
]
sage: es = A.eigenspaces_left(algebraic_multiplicity=True); es
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1], 1),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/15*a1 + 2/5 2/15*a1 - 1/5], 1)
]
sage: e, v, n = es[0]; v = v.basis()[0]
sage: delta = e*v - v*A
sage: abs(abs(delta)) < 1e-10
True
The same computation, but with implicit base change to a field:
sage: A = matrix(ZZ,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: A.eigenspaces_left()
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1]),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/15*a1 + 2/5 2/15*a1 - 1/5])
]
We compute the left eigenspaces of the matrix of the Hecke operator
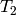 on level 43 modular symbols.
on level 43 modular symbols.
sage: A = ModularSymbols(43).T(2).matrix(); A
[ 3 0 0 0 0 0 -1]
[ 0 -2 1 0 0 0 0]
[ 0 -1 1 1 0 -1 0]
[ 0 -1 0 -1 2 -1 1]
[ 0 -1 0 1 1 -1 1]
[ 0 0 -2 0 2 -2 1]
[ 0 0 -1 0 1 0 -1]
sage: A.base_ring()
Rational Field
sage: f = A.charpoly(); f
x^7 + x^6 - 12*x^5 - 16*x^4 + 36*x^3 + 52*x^2 - 32*x - 48
sage: factor(f)
(x - 3) * (x + 2)^2 * (x^2 - 2)^2
sage: A.eigenspaces_left(algebraic_multiplicity=True)
[
(3, Vector space of degree 7 and dimension 1 over Rational Field
User basis matrix:
[ 1 0 1/7 0 -1/7 0 -2/7], 1),
(-2, Vector space of degree 7 and dimension 2 over Rational Field
User basis matrix:
[ 0 1 0 1 -1 1 -1]
[ 0 0 1 0 -1 2 -1], 2),
(a2, Vector space of degree 7 and dimension 2 over Number Field in a2 with defining polynomial x^2 - 2
User basis matrix:
[ 0 1 0 -1 -a2 - 1 1 -1]
[ 0 0 1 0 -1 0 -a2 + 1], 2)
]
Next we compute the left eigenspaces over the finite field of order 11:
sage: A = ModularSymbols(43, base_ring=GF(11), sign=1).T(2).matrix(); A
[ 3 9 0 0]
[ 0 9 0 1]
[ 0 10 9 2]
[ 0 9 0 2]
sage: A.base_ring()
Finite Field of size 11
sage: A.charpoly()
x^4 + 10*x^3 + 3*x^2 + 2*x + 1
sage: A.eigenspaces_left(var = 'beta')
[
(9, Vector space of degree 4 and dimension 1 over Finite Field of size 11
User basis matrix:
[0 0 1 5]),
(3, Vector space of degree 4 and dimension 1 over Finite Field of size 11
User basis matrix:
[1 6 0 6]),
(beta2, Vector space of degree 4 and dimension 1 over Univariate Quotient Polynomial Ring in beta2 over Finite Field of size 11 with modulus x^2 + 9
User basis matrix:
[ 0 1 0 5*beta2 + 10])
]
TESTS:
Warnings are issued if the generic algorithm is used over inexact fields. Garbage may result in these cases because of numerical precision issues.
sage: R=RealField(30)
sage: M=matrix(R,2,[2,1,1,1])
sage: M.eigenspaces_left() # random output from numerical issues
[
(2.6180340, Vector space of degree 2 and dimension 0 over Real Field with 30 bits of precision
User basis matrix:
[]),
(0.38196601, Vector space of degree 2 and dimension 0 over Real Field with 30 bits of precision
User basis matrix:
[])
]
sage: R=ComplexField(30)
sage: N=matrix(R,2,[2,1,1,1])
sage: N.eigenspaces_left() # random output from numerical issues
[
(2.6180340, Vector space of degree 2 and dimension 0 over Complex Field with 30 bits of precision
User basis matrix:
[]),
(0.38196601, Vector space of degree 2 and dimension 0 over Complex Field with 30 bits of precision
User basis matrix:
[])
]
Compute right eigenspaces of a matrix.
If algebraic_multiplicity=False, return a list of pairs (e, V) where e runs through all eigenvalues (up to Galois conjugation) of this matrix, and V is the corresponding right eigenspace.
If algebraic_multiplicity=True, return a list of pairs (e, V, n) where e and V are as above and n is the algebraic multiplicity of the eigenvalue. If the eigenvalues are given symbolically, as roots of an irreducible factor of the characteristic polynomial, then the algebraic multiplicity returned is the multiplicity of each conjugate eigenvalue.
The eigenspaces are returned sorted by the corresponding characteristic polynomials, where polynomials are sorted in dictionary order starting with constant terms.
INPUT:
Warning
Uses a somewhat naive algorithm (simply factors the characteristic polynomial and computes kernels directly over the extension field).
TODO: Maybe implement the better algorithm that is in dual_eigenvector in sage/modular/hecke/module.py.
EXAMPLES: We compute the right eigenspaces of a  rational matrix.
rational matrix.
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: es = A.eigenspaces_right(); es
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1]),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/5*a1 + 2/5 2/5*a1 - 1/5])
]
sage: es = A.eigenspaces_right(algebraic_multiplicity=True); es
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1], 1),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/5*a1 + 2/5 2/5*a1 - 1/5], 1)
]
sage: e, v, n = es[0]; v = v.basis()[0]
sage: delta = v*e - A*v
sage: abs(abs(delta)) < 1e-10
True
The same computation, but with implicit base change to a field:
sage: A = matrix(ZZ,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: A.eigenspaces_right()
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1]),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/5*a1 + 2/5 2/5*a1 - 1/5])
]
TESTS: Warnings are issued if the generic algorithm is used over inexact fields. Garbage may result in these cases because of numerical precision issues.
sage: R=RealField(30)
sage: M=matrix(R,2,[2,1,1,1])
sage: M.eigenspaces_right() # random output from numerical issues
[(2.6180340,
Vector space of degree 2 and dimension 0 over Real Field with 30 bits of precision
User basis matrix:
[]),
(0.38196601,
Vector space of degree 2 and dimension 0 over Real Field with 30 bits of precision
User basis matrix:
[])]
sage: R=ComplexField(30)
sage: N=matrix(R,2,[2,1,1,1])
sage: N.eigenspaces_right() # random output from numerical issues
[(2.6180340,
Vector space of degree 2 and dimension 0 over Complex Field with 30 bits of precision
User basis matrix:
[]),
(0.38196601,
Vector space of degree 2 and dimension 0 over Complex Field with 30 bits of precision
User basis matrix:
[])]
Return a sequence of the eigenvalues of a matrix, with multiplicity. If the eigenvalues are roots of polynomials in QQ, then QQbar elements are returned that represent each separate root.
EXAMPLES:
sage: a = matrix(QQ, 4, range(16)); a
[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
sage: sorted(a.eigenvalues(), reverse=True)
[32.46424919657298?, 0, 0, -2.464249196572981?]
sage: a=matrix([(1, 9, -1, -1), (-2, 0, -10, 2), (-1, 0, 15, -2), (0, 1, 0, -1)])
sage: a.eigenvalues()
[-0.9386318578049146?, 15.50655435353258?, 0.2160387521361705? - 4.713151979747493?*I, 0.2160387521361705? + 4.713151979747493?*I]
A symmetric matrix a+a.transpose() should have real eigenvalues
sage: b=a+a.transpose()
sage: ev = b.eigenvalues(); ev
[-8.35066086057957?, -1.107247901349379?, 5.718651326708515?, 33.73925743522043?]
The eigenvalues are elements of QQbar, so they really represent exact roots of polynomials, not just approximations.
sage: e = ev[0]; e
-8.35066086057957?
sage: p = e.minpoly(); p
x^4 - 30*x^3 - 171*x^2 + 1460*x + 1784
sage: p(e) == 0
True
To perform computations on the eigenvalue as an element of a number field, you can always convert back to a number field element.
sage: e.as_number_field_element()
(Number Field in a with defining polynomial y^4 - 2*y^3 - 507*y^2 + 4988*y - 8744,
-a + 8,
Ring morphism:
From: Number Field in a with defining polynomial y^4 - 2*y^3 - 507*y^2 + 4988*y - 8744
To: Algebraic Real Field
Defn: a |--> 16.35066086057957?)
Compute the left eigenvectors of a matrix.
For each distinct eigenvalue, returns a list of the form (e,V,n) where e is the eigenvalue, V is a list of eigenvectors forming a basis for the corresponding left eigenspace, and n is the algebraic multiplicity of the eigenvalue.
EXAMPLES: We compute the left eigenvectors of a  rational matrix.
rational matrix.
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: es = A.eigenvectors_left(); es
[(0, [
(1, -2, 1)
], 1),
(-1.348469228349535?, [(1, 0.3101020514433644?, -0.3797958971132713?)], 1),
(13.34846922834954?, [(1, 1.289897948556636?, 1.579795897113272?)], 1)]
sage: eval, [evec], mult = es[0]
sage: delta = eval*evec - evec*A
sage: abs(abs(delta)) < 1e-10
True
Compute the right eigenvectors of a matrix.
For each distinct eigenvalue, returns a list of the form (e,V,n) where e is the eigenvalue, V is a list of eigenvectors forming a basis for the corresponding right eigenspace, and n is the algebraic multiplicity of the eigenvalue.
EXAMPLES: We compute the right eigenvectors of a
 rational matrix.
rational matrix.
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: es = A.eigenvectors_right(); es
[(0, [
(1, -2, 1)
], 1),
(-1.348469228349535?, [(1, 0.1303061543300932?, -0.7393876913398137?)], 1),
(13.34846922834954?, [(1, 3.069693845669907?, 5.139387691339814?)], 1)]
sage: eval, [evec], mult = es[0]
sage: delta = eval*evec - A*evec
sage: abs(abs(delta)) < 1e-10
True
If self is a matrix over a principal ideal domain R, return
elements 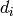 for
for 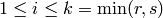 where
where  and
and  are the number of rows and
columns of self, such that the cokernel of self is isomorphic to
are the number of rows and
columns of self, such that the cokernel of self is isomorphic to

with 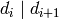 for all
for all  . These are
the diagonal entries of the Smith form of self (see
smith_form()).
. These are
the diagonal entries of the Smith form of self (see
smith_form()).
EXAMPLES:
sage: OE = EquationOrder(x^2 - x + 2, 'w')
sage: w = OE.ring_generators()[0]
sage: m = Matrix([ [1, w],[w,7]])
sage: m.elementary_divisors()
[1, -w + 9]
See also
Returns the elementwise product of two matrices of the same size (also known as the Hadamard product).
INPUT:
OUTPUT:
A matrix of the same size as self and right. The
entry in location 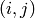 of the output is the product of
the two entries in location
of the output is the product of
the two entries in location 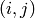 of self and
right (in that order).
of self and
right (in that order).
The parent of the result is determined by Sage’s coercion model. If the base rings are identical, then the result is dense or sparse according to this property for the left operand. If the base rings must be adjusted for one, or both, matrices then the result will be sparse only if both operands are sparse. No subdivisions are present in the result.
If the type of the result is not to your liking, or the ring could be “tighter,” adjust the operands with change_ring(). Adjust sparse versus dense inputs with the methods sparse_matrix() and dense_matrix().
EXAMPLES:
sage: A = matrix(ZZ, 2, range(6))
sage: B = matrix(QQ, 2, [5, 1/3, 2/7, 11/2, -3/2, 8])
sage: C = A.elementwise_product(B)
sage: C
[ 0 1/3 4/7]
[33/2 -6 40]
sage: C.parent()
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
Notice the base ring of the results in the next two examples.
sage: D = matrix(ZZ[x],2,[1+x^2,2,3,4-x])
sage: E = matrix(QQ,2,[1,2,3,4])
sage: F = D.elementwise_product(E)
sage: F
[ x^2 + 1 4]
[ 9 -4*x + 16]
sage: F.parent()
Full MatrixSpace of 2 by 2 dense matrices over Univariate Polynomial Ring in x over Rational Field
sage: G = matrix(GF(3),2,[0,1,2,2])
sage: H = matrix(ZZ,2,[1,2,3,4])
sage: J = G.elementwise_product(H)
sage: J
[0 2]
[0 2]
sage: J.parent()
Full MatrixSpace of 2 by 2 dense matrices over Finite Field of size 3
Non-commutative rings behave as expected. These are the usual quaternions.
sage: R.<i,j,k> = QuaternionAlgebra(-1, -1)
sage: A = matrix(R, 2, [1,i,j,k])
sage: B = matrix(R, 2, [i,i,i,i])
sage: A.elementwise_product(B)
[ i -1]
[-k j]
sage: B.elementwise_product(A)
[ i -1]
[ k -j]
Input that is not a matrix will raise an error.
sage: A = random_matrix(ZZ,5,10,x=20)
sage: A.elementwise_product(vector(ZZ, [1,2,3,4]))
...
TypeError: operand must be a matrix, not an element of Ambient free module of rank 4 over the principal ideal domain Integer Ring
Matrices of different sizes for operands will raise an error.
sage: A = random_matrix(ZZ,5,10,x=20)
sage: B = random_matrix(ZZ,10,5,x=40)
sage: A.elementwise_product(B)
...
TypeError: incompatible sizes for matrices from: Full MatrixSpace of 5 by 10 dense matrices over Integer Ring and Full MatrixSpace of 10 by 5 dense matrices over Integer Ring
Some pairs of rings do not have a common parent where multiplication makes sense. This will raise an error.
sage: A = matrix(QQ, 3, range(6))
sage: B = matrix(GF(3), 3, [2]*6)
sage: A.elementwise_product(B)
...
TypeError: no common canonical parent for objects with parents: 'Full MatrixSpace of 3 by 2 dense matrices over Rational Field' and 'Full MatrixSpace of 3 by 2 dense matrices over Finite Field of size 3'
We illustrate various combinations of sparse and dense matrices. Notice how if base rings are unequal, both operands must be sparse to get a sparse result. When the base rings are equal, the left operand dictates the sparse/dense property of the result. This behavior is entirely a consequence of the coercion model.
sage: A = matrix(ZZ, 5, range(30), sparse=False)
sage: B = matrix(ZZ, 5, range(30), sparse=True)
sage: C = matrix(QQ, 5, range(30), sparse=True)
sage: A.elementwise_product(C).is_dense()
True
sage: B.elementwise_product(C).is_sparse()
True
sage: A.elementwise_product(B).is_dense()
True
sage: B.elementwise_product(A).is_sparse()
True
TESTS:
Implementation for dense and sparse matrices are different, this will provide a trivial test that they are working identically.
sage: A = random_matrix(ZZ, 10, x=1000, sparse=False)
sage: B = random_matrix(ZZ, 10, x=1000, sparse=False)
sage: C = A.sparse_matrix()
sage: D = B.sparse_matrix()
sage: E = A.elementwise_product(B)
sage: F = C.elementwise_product(D)
sage: E.is_dense() and F.is_sparse() and (E == F)
True
If the ring has zero divisors, the routines for setting entries of a sparse matrix should intercept zero results and not create an entry.
sage: R = Integers(6)
sage: A = matrix(R, 2, [3, 2, 0, 0], sparse=True)
sage: B = matrix(R, 2, [2, 3, 1, 0], sparse=True)
sage: C = A.elementwise_product(B)
sage: len(C.nonzero_positions()) == 0
True
AUTHOR:
Calculate the exponential of this matrix X, which is the matrix

This function depends on maxima’s matrix exponentiation function, which does not deal well with floating point numbers. If the matrix has floating point numbers, they will be rounded automatically to rational numbers during the computation. If you want approximations to the exponential that are calculated numerically, you may get better results by first converting your matrix to RDF or CDF, as shown in the last example.
EXAMPLES:
sage: a=matrix([[1,2],[3,4]])
sage: a.exp()
[-1/22*((sqrt(33) - 11)*e^sqrt(33) - sqrt(33) - 11)*e^(-1/2*sqrt(33) + 5/2) 2/33*(sqrt(33)*e^sqrt(33) - sqrt(33))*e^(-1/2*sqrt(33) + 5/2)]
[ 1/11*(sqrt(33)*e^sqrt(33) - sqrt(33))*e^(-1/2*sqrt(33) + 5/2) 1/22*((sqrt(33) + 11)*e^sqrt(33) - sqrt(33) + 11)*e^(-1/2*sqrt(33) + 5/2)]
sage: type(a.exp())
<type 'sage.matrix.matrix_symbolic_dense.Matrix_symbolic_dense'>
sage: a=matrix([[1/2,2/3],[3/4,4/5]])
sage: a.exp()
[-1/418*((3*sqrt(209) - 209)*e^(1/10*sqrt(209)) - 3*sqrt(209) - 209)*e^(-1/20*sqrt(209) + 13/20) 20/627*(sqrt(209)*e^(1/10*sqrt(209)) - sqrt(209))*e^(-1/20*sqrt(209) + 13/20)]
[ 15/418*(sqrt(209)*e^(1/10*sqrt(209)) - sqrt(209))*e^(-1/20*sqrt(209) + 13/20) 1/418*((3*sqrt(209) + 209)*e^(1/10*sqrt(209)) - 3*sqrt(209) + 209)*e^(-1/20*sqrt(209) + 13/20)]
sage: a=matrix(RR,[[1,pi.n()],[1e2,1e-2]])
sage: a.exp()
[ 1/416296432702*((297*sqrt(382784569869489) + 208148216351)*e^(1/551700*sqrt(382784569869489)) - 297*sqrt(382784569869489) + 208148216351)*e^(-1/1103400*sqrt(382784569869489) + 101/200) 5199650/1148353709608467*(sqrt(382784569869489)*e^(1/551700*sqrt(382784569869489)) - sqrt(382784569869489))*e^(-1/1103400*sqrt(382784569869489) + 101/200)]
[ 30000/208148216351*(sqrt(382784569869489)*e^(1/551700*sqrt(382784569869489)) - sqrt(382784569869489))*e^(-1/1103400*sqrt(382784569869489) + 101/200) -1/416296432702*((297*sqrt(382784569869489) - 208148216351)*e^(1/551700*sqrt(382784569869489)) - 297*sqrt(382784569869489) - 208148216351)*e^(-1/1103400*sqrt(382784569869489) + 101/200)]
sage: a.change_ring(RDF).exp()
[42748127.3153 7368259.24416]
[234538976.138 40426191.4516]
Return the factorization of the characteristic polynomial of self.
INPUT:
EXAMPLES:
sage: M = MatrixSpace(QQ,3,3)
sage: A = M([1,9,-7,4/5,4,3,6,4,3])
sage: A.fcp()
x^3 - 8*x^2 + 209/5*x - 286
sage: A = M([3, 0, -2, 0, -2, 0, 0, 0, 0])
sage: A.fcp('T')
(T - 3) * T * (T + 2)
Find elements in this matrix satisfying the constraints in the
function 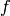 . The function is evaluated on each element of
the matrix .
. The function is evaluated on each element of
the matrix .
INPUT:
OUTPUT: If indices is not specified, return a
matrix with 1 where 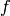 is satisfied and 0 where it is not.
If indices is specified, return a dictionary with
containing the elements of this matrix satisfying
is satisfied and 0 where it is not.
If indices is specified, return a dictionary with
containing the elements of this matrix satisfying 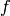 .
.
EXAMPLES:
sage: M = matrix(4,3,[1, -1/2, -1, 1, -1, -1/2, -1, 0, 0, 2, 0, 1])
sage: M.find(lambda entry:entry==0)
[0 0 0]
[0 0 0]
[0 1 1]
[0 1 0]
sage: M.find(lambda u:u<0)
[0 1 1]
[0 1 1]
[1 0 0]
[0 0 0]
sage: M = matrix(4,3,[1, -1/2, -1, 1, -1, -1/2, -1, 0, 0, 2, 0, 1])
sage: len(M.find(lambda u:u<1 and u>-1,indices=True))
5
sage: M.find(lambda u:u!=1/2)
[1 1 1]
[1 1 1]
[1 1 1]
[1 1 1]
sage: M.find(lambda u:u>1.2)
[0 0 0]
[0 0 0]
[0 0 0]
[1 0 0]
sage: sorted(M.find(lambda u:u!=0,indices=True).keys()) == M.nonzero_positions()
True
Returns the current subdivision of self.
EXAMPLES:
sage: M = matrix(5, 5, range(25))
sage: M.get_subdivisions()
([], [])
sage: M.subdivide(2,3)
sage: M.get_subdivisions()
([2], [3])
sage: N = M.parent()(1)
sage: N.subdivide(M.get_subdivisions()); N
[1 0 0|0 0]
[0 1 0|0 0]
[-----+---]
[0 0 1|0 0]
[0 0 0|1 0]
[0 0 0|0 1]
Return the matrix G whose rows are obtained from the rows of self (=A) by applying the Gram-Schmidt orthogonalization process. Also return the coefficients mu ij, i.e., a matrix mu such that (mu + 1)*G == A.
OUTPUT:
EXAMPLES:
sage: A = matrix(ZZ, 3, [-1, 2, 5, -11, 1, 1, 1, -1, -3]); A
[ -1 2 5]
[-11 1 1]
[ 1 -1 -3]
sage: G, mu = A.gram_schmidt()
sage: G
[ -1 2 5]
[ -52/5 -1/5 -2]
[ 2/187 36/187 -14/187]
sage: mu
[ 0 0 0]
[ 3/5 0 0]
[ -3/5 -7/187 0]
sage: G.row(0) * G.row(1)
0
sage: G.row(0) * G.row(2)
0
sage: G.row(1) * G.row(2)
0
The relation between mu and A is as follows:
sage: (mu + 1)*G == A
True
Return an int n such that the absolute value of the determinant of
this matrix is at most  .
.
This is got using both the row norms and the column norms.
This function only makes sense when the base field can be coerced to the real double field RDF or the MPFR Real Field with 53-bits precision.
EXAMPLES:
sage: a = matrix(ZZ, 3, [1,2,5,7,-3,4,2,1,123])
sage: a.hadamard_bound()
4
sage: a.det()
-2014
sage: 10^4
10000
In this example the Hadamard bound has to be computed (automatically) using MPFR instead of doubles, since doubles overflow:
sage: a = matrix(ZZ, 2, [2^10000,3^10000,2^50,3^19292])
sage: a.hadamard_bound()
12215
sage: len(str(a.det()))
12215
Return Hessenberg form of self.
If the base ring is merely an integral domain (and not a field), the Hessenberg form will (in general) only be defined over the fraction field of the base ring.
EXAMPLES:
sage: A = matrix(ZZ,4,[2, 1, 1, -2, 2, 2, -1, -1, -1,1,2,3,4,5,6,7])
sage: h = A.hessenberg_form(); h
[ 2 -7/2 -19/5 -2]
[ 2 1/2 -17/5 -1]
[ 0 25/4 15/2 5/2]
[ 0 0 58/5 3]
sage: parent(h)
Full MatrixSpace of 4 by 4 dense matrices over Rational Field
sage: A.hessenbergize()
...
TypeError: Hessenbergize only possible for matrices over a field
Transform self to Hessenberg form.
The hessenberg form of a matrix  is a matrix that is
similar to
is a matrix that is
similar to  , so has the same characteristic polynomial
as
, so has the same characteristic polynomial
as  , and is upper triangular except possible for entries
right below the diagonal.
, and is upper triangular except possible for entries
right below the diagonal.
ALGORITHM: See Henri Cohen’s first book.
EXAMPLES:
sage: A = matrix(QQ,3, [2, 1, 1, -2, 2, 2, -1, -1, -1])
sage: A.hessenbergize(); A
[ 2 3/2 1]
[ -2 3 2]
[ 0 -3 -2]
sage: A = matrix(QQ,4, [2, 1, 1, -2, 2, 2, -1, -1, -1,1,2,3,4,5,6,7])
sage: A.hessenbergize(); A
[ 2 -7/2 -19/5 -2]
[ 2 1/2 -17/5 -1]
[ 0 25/4 15/2 5/2]
[ 0 0 58/5 3]
You can’t Hessenbergize an immutable matrix:
sage: A = matrix(QQ, 3, [1..9])
sage: A.set_immutable()
sage: A.hessenbergize()
...
ValueError: matrix is immutable; please change a copy instead (i.e., use copy(M) to change a copy of M).
Return the image of the homomorphism on rows defined by this matrix.
EXAMPLES:
sage: MS1 = MatrixSpace(ZZ,4)
sage: MS2 = MatrixSpace(QQ,6)
sage: A = MS1.matrix([3,4,5,6,7,3,8,10,14,5,6,7,2,2,10,9])
sage: B = MS2.random_element()
sage: image(A)
Free module of degree 4 and rank 4 over Integer Ring
Echelon basis matrix:
[ 1 0 0 426]
[ 0 1 0 518]
[ 0 0 1 293]
[ 0 0 0 687]
sage: image(B) == B.row_module()
True
Return the kernel of this matrix over the given ring (which should be either the base ring, or a PID whose fraction field is the base ring).
Assume that the base field of this matrix has a numerator and denominator functions for its elements, e.g., it is the rational numbers or a fraction field. This function computes a basis over the integers for the kernel of self.
If the matrix is not coercible into QQ, then the PID itself should be given as a second argument, as in the third example below.
EXAMPLES:
sage: A = MatrixSpace(QQ, 4)(range(16))
sage: A.integer_kernel()
Free module of degree 4 and rank 2 over Integer Ring
Echelon basis matrix:
[ 1 0 -3 2]
[ 0 1 -2 1]
The integer kernel even makes sense for matrices with fractional entries:
sage: A = MatrixSpace(QQ, 2)(['1/2',0, 0, 0])
sage: A.integer_kernel()
Free module of degree 2 and rank 1 over Integer Ring
Echelon basis matrix:
[0 1]
An example over a bigger ring:
sage: L.<w> = NumberField(x^2 - x + 2)
sage: OL = L.ring_of_integers()
sage: A = matrix(L, 2, [1, w/2])
sage: A.integer_kernel(OL)
Free module of degree 2 and rank 1 over Maximal Order in Number Field in w with defining polynomial x^2 - x + 2
Echelon basis matrix:
[ -1 -w + 1]
Returns the inverse of self, without changing self.
Note that one can use the Python inverse operator to obtain the inverse as well.
EXAMPLES:
sage: m = matrix([[1,2],[3,4]])
sage: m^(-1)
[ -2 1]
[ 3/2 -1/2]
sage: m.inverse()
[ -2 1]
[ 3/2 -1/2]
sage: ~m
[ -2 1]
[ 3/2 -1/2]
sage: m = matrix([[1,2],[3,4]], sparse=True)
sage: m^(-1)
[ -2 1]
[ 3/2 -1/2]
sage: m.inverse()
[ -2 1]
[ 3/2 -1/2]
sage: ~m
[ -2 1]
[ 3/2 -1/2]
TESTS:
sage: matrix().inverse()
[]
Returns True if this matrix is bistochastic.
A matrix is said to be bistochastic if both the sums of the entries of each row and the sum of the entries of each column are equal to 1.
INPUT:
EXAMPLES:
The identity matrix is clearly bistochastic:
sage: Matrix(5,5,1).is_bistochastic()
True
The same matrix, multiplied by 2, is not bistochastic anymore, though is verifies the constraints of normalized == False:
sage: (2 * Matrix(5,5,1)).is_bistochastic()
False
sage: (2 * Matrix(5,5,1)).is_bistochastic(normalized = False)
True
Return True if this matrix is the identity matrix.
EXAMPLES:
sage: m = matrix(QQ,2,range(4))
sage: m.is_one()
False
sage: m = matrix(QQ,2,[5,0,0,5])
sage: m.is_one()
False
sage: m = matrix(QQ,2,[1,0,0,1])
sage: m.is_one()
True
sage: m = matrix(QQ,2,[1,1,1,1])
sage: m.is_one()
False
Return True if this matrix is a scalar matrix.
INPUT
OUTPUT
EXAMPLES:
sage: m = matrix(QQ,2,range(4))
sage: m.is_scalar(5)
False
sage: m = matrix(QQ,2,[5,0,0,5])
sage: m.is_scalar(5)
True
sage: m = matrix(QQ,2,[1,0,0,1])
sage: m.is_scalar(1)
True
sage: m = matrix(QQ,2,[1,1,1,1])
sage: m.is_scalar(1)
False
Compute the Jordan normal form of this square matrix  , if it exists.
, if it exists.
This computation is performed in a naive way using the ranks of powers
of 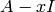 , where
, where  is an eigenvalue of the matrix
is an eigenvalue of the matrix  . If desired,
a transformation matrix
. If desired,
a transformation matrix 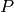 can be returned, which is such that the
Jordan canonical form is given by
can be returned, which is such that the
Jordan canonical form is given by  .
.
INPUT:
NOTES:
Currently, the Jordan normal form is not computed over inexact rings
in any but the trivial cases when the matrix is either  or
or  .
.
In the case of exact rings, this method does not compute any generalized form of the Jordan normal form, but is only able to compute the result if the characteristic polynomial of the matrix splits over the specific base ring.
EXAMPLES:
sage: a = matrix(ZZ,4,[1, 0, 0, 0, 0, 1, 0, 0, 1, \
-1, 1, 0, 1, -1, 1, 2]); a
[ 1 0 0 0]
[ 0 1 0 0]
[ 1 -1 1 0]
[ 1 -1 1 2]
sage: a.jordan_form()
[2|0 0|0]
[-+---+-]
[0|1 1|0]
[0|0 1|0]
[-+---+-]
[0|0 0|1]
sage: a.jordan_form(subdivide=False)
[2 0 0 0]
[0 1 1 0]
[0 0 1 0]
[0 0 0 1]
sage: b = matrix(ZZ,3,range(9)); b
[0 1 2]
[3 4 5]
[6 7 8]
sage: b.jordan_form()
...
RuntimeError: Some eigenvalue does not exist in Integer Ring.
sage: b.jordan_form(RealField(15))
...
ValueError: Jordan normal form not implemented over inexact rings.
If you need the transformation matrix as well as the Jordan form of self, then pass the option transformation=True.
sage: m = matrix([[5,4,2,1],[0,1,-1,-1],[-1,-1,3,0],[1,1,-1,2]]); m
[ 5 4 2 1]
[ 0 1 -1 -1]
[-1 -1 3 0]
[ 1 1 -1 2]
sage: jf, p = m.jordan_form(transformation=True)
sage: jf
[2|0|0 0]
[-+-+---]
[0|1|0 0]
[-+-+---]
[0|0|4 1]
[0|0|0 4]
sage: ~p * m * p
[2 0 0 0]
[0 1 0 0]
[0 0 4 1]
[0 0 0 4]
Note that for matrices over inexact rings and associated numerical stability problems, we do not attempt to compute the Jordan normal form.
sage: b = matrix(ZZ,3,3,range(9))
sage: jf, p = b.jordan_form(RealField(15), transformation=True)
...
ValueError: Jordan normal form not implemented over inexact rings.
TESTS:
sage: c = matrix(ZZ, 3, [1]*9); c
[1 1 1]
[1 1 1]
[1 1 1]
sage: c.jordan_form(subdivide=False)
[3 0 0]
[0 0 0]
[0 0 0]
sage: evals = [(i,i) for i in range(1,6)]
sage: n = sum(range(1,6))
sage: jf = block_diagonal_matrix([jordan_block(ev,size) for ev,size in evals])
sage: p = random_matrix(ZZ,n,n)
sage: while p.rank() != n: p = random_matrix(ZZ,n,n)
sage: m = p * jf * ~p
sage: mjf, mp = m.jordan_form(transformation=True)
sage: mjf == jf
True
sage: m = diagonal_matrix([1,1,0,0])
sage: jf,P = m.jordan_form(transformation=True)
sage: jf == ~P*m*P
True
We verify that the bug from trac ticket #6942 is fixed:
sage: M = Matrix(GF(2),[[1,0,1,0,0,0,1],[1,0,0,1,1,1,0],[1,1,0,1,1,1,1],[1,1,1,0,1,1,1],[1,1,1,0,0,1,0],[1,1,1,0,1,0,0],[1,1,1,1,1,1,0]])
sage: J, T = M.jordan_form(transformation=True)
sage: J
[1 1|0 0|0 0|0]
[0 1|0 0|0 0|0]
[---+---+---+-]
[0 0|1 1|0 0|0]
[0 0|0 1|0 0|0]
[---+---+---+-]
[0 0|0 0|1 1|0]
[0 0|0 0|0 1|0]
[---+---+---+-]
[0 0|0 0|0 0|1]
sage: M * T == T * J
True
sage: T.rank()
7
sage: M.rank()
7
We verify that the bug from trac ticket #6932 is fixed:
sage: M=Matrix(1,1,[1])
sage: M.jordan_form(transformation=True)
([1], [1])
We now go through three  matrices to exhibit cases where
there are multiple blocks of the same size:
matrices to exhibit cases where
there are multiple blocks of the same size:
sage: A = matrix(QQ, [[15, 37/3, -16, -104/3, -29, -7/3, 0, 2/3, -29/3, -1/3], [2, 9, -1, -6, -6, 0, 0, 0, -2, 0], [24, 74/3, -41, -208/3, -58, -23/3, 0, 4/3, -58/3, -2/3], [-6, -19, 3, 21, 19, 0, 0, 0, 6, 0], [2, 6, 3, -6, -3, 1, 0, 0, -2, 0], [-96, -296/3, 176, 832/3, 232, 101/3, 0, -16/3, 232/3, 8/3], [-4, -2/3, 21, 16/3, 4, 14/3, 3, -1/3, 4/3, -25/3], [20, 26/3, -66, -199/3, -42, -41/3, 0, 13/3, -55/3, -2/3], [18, 57, -9, -54, -57, 0, 0, 0, -15, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 3]]); A
[ 15 37/3 -16 -104/3 -29 -7/3 0 2/3 -29/3 -1/3]
[ 2 9 -1 -6 -6 0 0 0 -2 0]
[ 24 74/3 -41 -208/3 -58 -23/3 0 4/3 -58/3 -2/3]
[ -6 -19 3 21 19 0 0 0 6 0]
[ 2 6 3 -6 -3 1 0 0 -2 0]
[ -96 -296/3 176 832/3 232 101/3 0 -16/3 232/3 8/3]
[ -4 -2/3 21 16/3 4 14/3 3 -1/3 4/3 -25/3]
[ 20 26/3 -66 -199/3 -42 -41/3 0 13/3 -55/3 -2/3]
[ 18 57 -9 -54 -57 0 0 0 -15 0]
[ 0 0 0 0 0 0 0 0 0 3]
sage: J, T = A.jordan_form(transformation=True); J
[3 1 0|0 0 0|0 0 0|0]
[0 3 1|0 0 0|0 0 0|0]
[0 0 3|0 0 0|0 0 0|0]
[-----+-----+-----+-]
[0 0 0|3 1 0|0 0 0|0]
[0 0 0|0 3 1|0 0 0|0]
[0 0 0|0 0 3|0 0 0|0]
[-----+-----+-----+-]
[0 0 0|0 0 0|3 1 0|0]
[0 0 0|0 0 0|0 3 1|0]
[0 0 0|0 0 0|0 0 3|0]
[-----+-----+-----+-]
[0 0 0|0 0 0|0 0 0|3]
sage: T * J * T**(-1) == A
True
sage: T.rank()
10
sage: A = matrix(QQ, [[15, 37/3, -16, -14/3, -29, -7/3, 0, 2/3, 1/3, 44/3], [2, 9, -1, 0, -6, 0, 0, 0, 0, 3], [24, 74/3, -41, -28/3, -58, -23/3, 0, 4/3, 2/3, 88/3], [-6, -19, 3, 3, 19, 0, 0, 0, 0, -9], [2, 6, 3, 0, -3, 1, 0, 0, 0, 3], [-96, -296/3, 176, 112/3, 232, 101/3, 0, -16/3, -8/3, -352/3], [-4, -2/3, 21, 16/3, 4, 14/3, 3, -1/3, 4/3, -25/3], [20, 26/3, -66, -28/3, -42, -41/3, 0, 13/3, 2/3, 82/3], [18, 57, -9, 0, -57, 0, 0, 0, 3, 28], [0, 0, 0, 0, 0, 0, 0, 0, 0, 3]]); A
[ 15 37/3 -16 -14/3 -29 -7/3 0 2/3 1/3 44/3]
[ 2 9 -1 0 -6 0 0 0 0 3]
[ 24 74/3 -41 -28/3 -58 -23/3 0 4/3 2/3 88/3]
[ -6 -19 3 3 19 0 0 0 0 -9]
[ 2 6 3 0 -3 1 0 0 0 3]
[ -96 -296/3 176 112/3 232 101/3 0 -16/3 -8/3 -352/3]
[ -4 -2/3 21 16/3 4 14/3 3 -1/3 4/3 -25/3]
[ 20 26/3 -66 -28/3 -42 -41/3 0 13/3 2/3 82/3]
[ 18 57 -9 0 -57 0 0 0 3 28]
[ 0 0 0 0 0 0 0 0 0 3]
sage: J, T = A.jordan_form(transformation=True); J
[3 1 0|0 0 0|0 0|0 0]
[0 3 1|0 0 0|0 0|0 0]
[0 0 3|0 0 0|0 0|0 0]
[-----+-----+---+---]
[0 0 0|3 1 0|0 0|0 0]
[0 0 0|0 3 1|0 0|0 0]
[0 0 0|0 0 3|0 0|0 0]
[-----+-----+---+---]
[0 0 0|0 0 0|3 1|0 0]
[0 0 0|0 0 0|0 3|0 0]
[-----+-----+---+---]
[0 0 0|0 0 0|0 0|3 1]
[0 0 0|0 0 0|0 0|0 3]
sage: T * J * T**(-1) == A
True
sage: T.rank()
10
sage: A = matrix(QQ, [[15, 37/3, -16, -104/3, -29, -7/3, 35, 2/3, -29/3, -1/3], [2, 9, -1, -6, -6, 0, 7, 0, -2, 0], [24, 74/3, -29, -208/3, -58, -14/3, 70, 4/3, -58/3, -2/3], [-6, -19, 3, 21, 19, 0, -21, 0, 6, 0], [2, 6, -1, -6, -3, 0, 7, 0, -2, 0], [-96, -296/3, 128, 832/3, 232, 65/3, -279, -16/3, 232/3, 8/3], [0, 0, 0, 0, 0, 0, 3, 0, 0, 0], [20, 26/3, -30, -199/3, -42, -14/3, 70, 13/3, -55/3, -2/3], [18, 57, -9, -54, -57, 0, 63, 0, -15, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 3]]); A
[ 15 37/3 -16 -104/3 -29 -7/3 35 2/3 -29/3 -1/3]
[ 2 9 -1 -6 -6 0 7 0 -2 0]
[ 24 74/3 -29 -208/3 -58 -14/3 70 4/3 -58/3 -2/3]
[ -6 -19 3 21 19 0 -21 0 6 0]
[ 2 6 -1 -6 -3 0 7 0 -2 0]
[ -96 -296/3 128 832/3 232 65/3 -279 -16/3 232/3 8/3]
[ 0 0 0 0 0 0 3 0 0 0]
[ 20 26/3 -30 -199/3 -42 -14/3 70 13/3 -55/3 -2/3]
[ 18 57 -9 -54 -57 0 63 0 -15 0]
[ 0 0 0 0 0 0 0 0 0 3]
sage: J, T = A.jordan_form(transformation=True); J
[3 1 0|0 0|0 0|0 0|0]
[0 3 1|0 0|0 0|0 0|0]
[0 0 3|0 0|0 0|0 0|0]
[-----+---+---+---+-]
[0 0 0|3 1|0 0|0 0|0]
[0 0 0|0 3|0 0|0 0|0]
[-----+---+---+---+-]
[0 0 0|0 0|3 1|0 0|0]
[0 0 0|0 0|0 3|0 0|0]
[-----+---+---+---+-]
[0 0 0|0 0|0 0|3 1|0]
[0 0 0|0 0|0 0|0 3|0]
[-----+---+---+---+-]
[0 0 0|0 0|0 0|0 0|3]
sage: T * J * T**(-1) == A
True
sage: T.rank()
10
Return the (left) kernel of this matrix, as a vector space. This is the space of vectors x such that x*self=0. Use self.right_kernel() for the right kernel, while self.left_kernel() is equivalent to self.kernel().
INPUT: all additional arguments to the kernel function are passed directly onto the echelon call.
By convention if self has 0 rows, the kernel is of dimension 0, whereas the kernel is whole domain if self has 0 columns.
Note
For information on algorithms used, see the documentation of right_kernel() in this class, or versions of right and left kernels in derived classes which override the ones here.
EXAMPLES:
A kernel of dimension one over  :
:
sage: A = MatrixSpace(QQ, 3)(range(9))
sage: A.kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2 1]
A trivial kernel:
sage: A = MatrixSpace(QQ, 2)([1,2,3,4])
sage: A.kernel()
Vector space of degree 2 and dimension 0 over Rational Field
Basis matrix:
[]
Kernel of a zero matrix:
sage: A = MatrixSpace(QQ, 2)(0)
sage: A.kernel()
Vector space of degree 2 and dimension 2 over Rational Field
Basis matrix:
[1 0]
[0 1]
Kernel of a non-square matrix:
sage: A = MatrixSpace(QQ,3,2)(range(6))
sage: A.kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2 1]
The 2-dimensional kernel of a matrix over a cyclotomic field:
sage: K = CyclotomicField(12); a=K.0
sage: M = MatrixSpace(K,4,2)([1,-1, 0,-2, 0,-a**2-1, 0,a**2-1])
sage: M
[ 1 -1]
[ 0 -2]
[ 0 -zeta12^2 - 1]
[ 0 zeta12^2 - 1]
sage: M.kernel()
Vector space of degree 4 and dimension 2 over Cyclotomic Field of order 12 and degree 4
Basis matrix:
[ 0 1 0 -2*zeta12^2]
[ 0 0 1 -2*zeta12^2 + 1]
A nontrivial kernel over a complicated base field.
sage: K = FractionField(PolynomialRing(QQ, 2, 'x'))
sage: M = MatrixSpace(K, 2)([[K.1, K.0], [K.1, K.0]])
sage: M
[x1 x0]
[x1 x0]
sage: M.kernel()
Vector space of degree 2 and dimension 1 over Fraction Field of Multivariate Polynomial Ring in x0, x1 over Rational Field
Basis matrix:
[ 1 -1]
We test a trivial left kernel over ZZ:
sage: id = matrix(ZZ, 2, 2, [[1, 0], [0, 1]])
sage: id.left_kernel()
Free module of degree 2 and rank 0 over Integer Ring
Echelon basis matrix:
[]
Another matrix over ZZ.
sage: a = matrix(ZZ,3,1,[1,2,3])
sage: a.left_kernel()
Free module of degree 3 and rank 2 over Integer Ring
Echelon basis matrix:
[ 1 1 -1]
[ 0 3 -2]
Kernel of a large dense rational matrix, which will invoke the fast IML routines in matrix_integer_dense class. Timing on a 64-bit 3 GHz dual-core machine is about 3 seconds to setup and about 1 second for the kernel() call. Timings that are one or two orders of magnitude larger indicate problems with reaching specialized derived classes.
sage: entries = [[1/(i+j+1) for i in srange(500)] for j in srange(500)]
sage: a = matrix(QQ, entries)
sage: a.kernel()
Vector space of degree 500 and dimension 0 over Rational Field
Basis matrix:
0 x 500 dense matrix over Rational Field
Return the kernel of self restricted to the invariant subspace V. The result is a vector subspace of V, which is also a subspace of the ambient space.
INPUT:
OUTPUT:
Warning
This function does not check that V is in fact invariant under self if check is False. With check False this function is much faster.
EXAMPLES:
sage: t = matrix(QQ, 4, [39, -10, 0, -12, 0, 2, 0, -1, 0, 1, -2, 0, 0, 2, 0, -2]); t
[ 39 -10 0 -12]
[ 0 2 0 -1]
[ 0 1 -2 0]
[ 0 2 0 -2]
sage: t.fcp()
(x - 39) * (x + 2) * (x^2 - 2)
sage: s = (t-39)*(t^2-2)
sage: V = s.kernel(); V
Vector space of degree 4 and dimension 3 over Rational Field
Basis matrix:
[1 0 0 0]
[0 1 0 0]
[0 0 0 1]
sage: s.restrict(V)
[0 0 0]
[0 0 0]
[0 0 0]
sage: s.kernel_on(V)
Vector space of degree 4 and dimension 3 over Rational Field
Basis matrix:
[1 0 0 0]
[0 1 0 0]
[0 0 0 1]
sage: k = t-39
sage: k.restrict(V)
[ 0 -10 -12]
[ 0 -37 -1]
[ 0 2 -41]
sage: ker = k.kernel_on(V); ker
Vector space of degree 4 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2/7 0 -2/7]
sage: ker.0 * k
(0, 0, 0, 0)
Return matrices D and P, where D is a diagonal matrix of eigenvalues and P is the corresponding matrix where the rows are corresponding eigenvectors (or zero vectors) so that P*self = D*P.
EXAMPLES:
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: D, P = A.eigenmatrix_left()
sage: D
[ 0 0 0]
[ 0 -1.348469228349535? 0]
[ 0 0 13.34846922834954?]
sage: P
[ 1 -2 1]
[ 1 0.3101020514433644? -0.3797958971132713?]
[ 1 1.289897948556636? 1.579795897113272?]
sage: P*A == D*P
True
Because P is invertible, A is diagonalizable.
sage: A == (~P)*D*P
True
The matrix P may contain zero rows corresponding to eigenvalues for which the algebraic multiplicity is greater than the geometric multiplicity. In these cases, the matrix is not diagonalizable.
sage: A = jordan_block(2,3); A
[2 1 0]
[0 2 1]
[0 0 2]
sage: A = jordan_block(2,3)
sage: D, P = A.eigenmatrix_left()
sage: D
[2 0 0]
[0 2 0]
[0 0 2]
sage: P
[0 0 1]
[0 0 0]
[0 0 0]
sage: P*A == D*P
True
Compute the left eigenvectors of a matrix.
For each distinct eigenvalue, returns a list of the form (e,V,n) where e is the eigenvalue, V is a list of eigenvectors forming a basis for the corresponding left eigenspace, and n is the algebraic multiplicity of the eigenvalue.
EXAMPLES: We compute the left eigenvectors of a  rational matrix.
rational matrix.
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: es = A.eigenvectors_left(); es
[(0, [
(1, -2, 1)
], 1),
(-1.348469228349535?, [(1, 0.3101020514433644?, -0.3797958971132713?)], 1),
(13.34846922834954?, [(1, 1.289897948556636?, 1.579795897113272?)], 1)]
sage: eval, [evec], mult = es[0]
sage: delta = eval*evec - evec*A
sage: abs(abs(delta)) < 1e-10
True
Return the left kernel of this matrix, as a vector space. This is the space of vectors x such that x*self=0. This is identical to self.kernel(). For a right kernel, use self.right_kernel().
INPUT:
By convention if self has 0 columns, the kernel is of dimension 0, whereas the kernel is whole domain if self has 0 rows.
Note
For information on algorithms used, see the documentation of right_kernel() in this class, or versions of right and left kernels in derived classes which override the ones here.
EXAMPLES:
A left kernel of dimension one over  :
:
sage: A = MatrixSpace(QQ, 3)(range(9))
sage: A.left_kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2 1]
A trivial left kernel:
sage: A = MatrixSpace(QQ, 2)([1,2,3,4])
sage: A.left_kernel()
Vector space of degree 2 and dimension 0 over Rational Field
Basis matrix:
[]
Left kernel of a zero matrix:
sage: A = MatrixSpace(QQ, 2)(0)
sage: A.left_kernel()
Vector space of degree 2 and dimension 2 over Rational Field
Basis matrix:
[1 0]
[0 1]
Left kernel of a non-square matrix:
sage: A = MatrixSpace(QQ,3,2)(range(6))
sage: A.left_kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2 1]
The 2-dimensional left kernel of a matrix over a cyclotomic field:
sage: K = CyclotomicField(12); a=K.0
sage: M = MatrixSpace(K,4,2)([1,-1, 0,-2, 0,-a**2-1, 0,a**2-1])
sage: M
[ 1 -1]
[ 0 -2]
[ 0 -zeta12^2 - 1]
[ 0 zeta12^2 - 1]
sage: M.left_kernel()
Vector space of degree 4 and dimension 2 over Cyclotomic Field of order 12 and degree 4
Basis matrix:
[ 0 1 0 -2*zeta12^2]
[ 0 0 1 -2*zeta12^2 + 1]
A nontrivial left kernel over a complicated base field.
sage: K = FractionField(PolynomialRing(QQ, 2, 'x'))
sage: M = MatrixSpace(K, 2)([[K.1, K.0], [K.1, K.0]])
sage: M
[x1 x0]
[x1 x0]
sage: M.left_kernel()
Vector space of degree 2 and dimension 1 over Fraction Field of Multivariate Polynomial Ring in x0, x1 over Rational Field
Basis matrix:
[ 1 -1]
Left kernel of a large dense rational matrix, which will invoke the fast IML routines in matrix_integer_dense class. Timing on a 64-bit 3 GHz dual-core machine is about 3 seconds to setup and about 1 second for the kernel() call. Timings that are one or two orders of magnitude larger indicate problems with reaching specialized derived classes.
sage: entries = [[1/(i+j+1) for i in srange(500)] for j in srange(500)]
sage: a = matrix(QQ, entries)
sage: a.left_kernel()
Vector space of degree 500 and dimension 0 over Rational Field
Basis matrix:
0 x 500 dense matrix over Rational Field
Return the (left) nullity of this matrix, which is the dimension of the (left) kernel of this matrix acting from the right on row vectors.
EXAMPLES:
sage: M = Matrix(QQ,[[1,0,0,1],[0,1,1,0],[1,1,1,0]])
sage: M.nullity()
0
sage: M.left_nullity()
0
sage: A = M.transpose()
sage: A.nullity()
1
sage: A.left_nullity()
1
sage: M = M.change_ring(ZZ)
sage: M.nullity()
0
sage: A = M.transpose()
sage: A.nullity()
1
Return the requested matrix window.
EXAMPLES:
sage: A = matrix(QQ, 3, range(9))
sage: A.matrix_window(1,1, 2, 1)
Matrix window of size 2 x 1 at (1,1):
[0 1 2]
[3 4 5]
[6 7 8]
We test the optional check flag.
sage: matrix([1]).matrix_window(0,1,1,1, check=False)
Matrix window of size 1 x 1 at (0,1):
[1]
sage: matrix([1]).matrix_window(0,1,1,1)
...
IndexError: matrix window index out of range
Another test of bounds checking:
sage: matrix([1]).matrix_window(1,1,1,1)
...
IndexError: matrix window index out of range
Computes the largest integer n such that the list of vectors
![S=[v, v*A, ..., v * A^n]](../../_images/math/3321f7712c1d3ac0f77191bc99c0d768dd6bbb68.png) are linearly independent, and
returns that list.
are linearly independent, and
returns that list.
INPUT:
OUTPUT:
ALGORITHM: The current implementation just adds vectors to a vector space until the dimension doesn’t grow. This could be optimized by directly using matrices and doing an efficient Echelon form. Also, when the base is Q, maybe we could simultaneously keep track of what is going on in the reduction modulo p, which might make things much faster.
EXAMPLES:
sage: t = matrix(QQ, 3, range(9)); t
[0 1 2]
[3 4 5]
[6 7 8]
sage: v = (QQ^3).0
sage: t.maxspin(v)
[(1, 0, 0), (0, 1, 2), (15, 18, 21)]
sage: k = t.kernel(); k
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2 1]
sage: t.maxspin(k.0)
[(1, -2, 1)]
This is a synonym for self.minpoly
EXAMPLES:
sage: a = matrix(QQ, 4, range(16))
sage: a.minimal_polynomial('z')
z^3 - 30*z^2 - 80*z
sage: a.minpoly()
x^3 - 30*x^2 - 80*x
Return the list of all k-minors of self.
Let A be an m x n matrix and k an integer with 0 < k, k <= m, and k <= n. A k x k minor of A is the determinant of a k x k matrix obtained from A by deleting m - k rows and n - k columns.
The returned list is sorted in lexicographical row major ordering, e.g., if A is a 3 x 3 matrix then the minors returned are with for these rows/columns: [ [0, 1]x[0, 1], [0, 1]x[0, 2], [0, 1]x[1, 2], [0, 2]x[0, 1], [0, 2]x[0, 2], [0, 2]x[1, 2], [1, 2]x[0, 1], [1, 2]x[0, 2], [1, 2]x[1, 2] ].
INPUT:
EXAMPLE:
sage: A = Matrix(ZZ,2,3,[1,2,3,4,5,6]); A
[1 2 3]
[4 5 6]
sage: A.minors(2)
[-3, -6, -3]
sage: k = GF(37)
sage: P.<x0,x1,x2> = PolynomialRing(k)
sage: A = Matrix(P,2,3,[x0*x1, x0, x1, x2, x2 + 16, x2 + 5*x1 ])
sage: A.minors(2)
[x0*x1*x2 + 16*x0*x1 - x0*x2, 5*x0*x1^2 + x0*x1*x2 - x1*x2, 5*x0*x1 + x0*x2 - x1*x2 - 16*x1]
Return the minimal polynomial of self.
This uses a simplistic - and potentially very very slow - algorithm that involves computing kernels to determine the powers of the factors of the charpoly that divide the minpoly.
EXAMPLES:
sage: A = matrix(GF(9,'c'), 4, [1, 1, 0,0, 0,1,0,0, 0,0,5,0, 0,0,0,5])
sage: factor(A.minpoly())
(x + 1) * (x + 2)^2
sage: A.minpoly()(A) == 0
True
sage: factor(A.charpoly())
(x + 1)^2 * (x + 2)^2
The default variable name is  , but you can specify
another name:
, but you can specify
another name:
sage: factor(A.minpoly('y'))
(y + 1) * (y + 2)^2
We can take the minimal polynomail of symbolic matrices:
sage: t = var('t')
sage: m = matrix(2,[1,2,4,t])
sage: m.minimal_polynomial()
x^2 + (-t - 1)*x + t - 8
Return the p-norm of this matrix, where  can be 1, 2,
can be 1, 2,
 , or the Frobenius norm.
, or the Frobenius norm.
INPUT:
OUTPUT: RDF number
EXAMPLES:
sage: A = matrix(ZZ, [[1,2,4,3],[-1,0,3,-10]])
sage: A.norm(1)
13.0
sage: A.norm(Infinity)
14.0
sage: B = random_matrix(QQ, 20, 21)
sage: B.norm(Infinity) == (B.transpose()).norm(1)
True
sage: Id = identity_matrix(12)
sage: Id.norm(2)
1.0
sage: A = matrix(RR, 2, 2, [13,-4,-4,7])
sage: A.norm()
15.0
sage: A = matrix(CDF, 2, 3, [3*I,4,1-I,1,2,0])
sage: A.norm('frob')
5.65685424949
sage: A.norm(2)
5.47068444321
sage: A.norm(1)
6.0
sage: A.norm(Infinity)
8.41421356237
sage: a = matrix([[],[],[],[]])
sage: a.norm()
0.0
sage: a.norm(Infinity) == a.norm(1)
True
Return the (left) nullity of this matrix, which is the dimension of the (left) kernel of this matrix acting from the right on row vectors.
EXAMPLES:
sage: M = Matrix(QQ,[[1,0,0,1],[0,1,1,0],[1,1,1,0]])
sage: M.nullity()
0
sage: M.left_nullity()
0
sage: A = M.transpose()
sage: A.nullity()
1
sage: A.left_nullity()
1
sage: M = M.change_ring(ZZ)
sage: M.nullity()
0
sage: A = M.transpose()
sage: A.nullity()
1
Return a numerical approximation of self as either a real or complex number with at least the requested number of bits or digits of precision.
INPUT:
OUTPUT: A matrix coerced to a real or complex field with prec bits of precision.
EXAMPLES:
sage: d = matrix([[3, 0],[0,sqrt(2)]]) ;
sage: b = matrix([[1, -1], [2, 2]]) ; e = b * d * b.inverse();e
[ 1/2*sqrt(2) + 3/2 -1/4*sqrt(2) + 3/4]
[ -sqrt(2) + 3 1/2*sqrt(2) + 3/2]
sage: e.numerical_approx(53)
[ 2.20710678118655 0.396446609406726]
[ 1.58578643762690 2.20710678118655]
sage: e.numerical_approx(20)
[ 2.2071 0.39645]
[ 1.5858 2.2071]
sage: (e-I).numerical_approx(20)
[2.2071 - 1.0000*I 0.39645]
[ 1.5858 2.2071 - 1.0000*I]
sage: M=matrix(QQ,4,[i/(i+1) for i in range(12)]);M
[ 0 1/2 2/3]
[ 3/4 4/5 5/6]
[ 6/7 7/8 8/9]
[ 9/10 10/11 11/12]
sage: M.numerical_approx()
[0.000000000000000 0.500000000000000 0.666666666666667]
[0.750000000000000 0.800000000000000 0.833333333333333]
[0.857142857142857 0.875000000000000 0.888888888888889]
[0.900000000000000 0.909090909090909 0.916666666666667]
sage: matrix(SR, 2, 2, range(4)).n()
[0.000000000000000 1.00000000000000]
[ 2.00000000000000 3.00000000000000]
Calculate and return the permanent of this 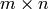 matrix using Ryser’s algorithm.
matrix using Ryser’s algorithm.
Let  be an
be an 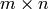 matrix over
any commutative ring, with
matrix over
any commutative ring, with 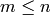 . The permanent of
. The permanent of
 is
is
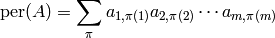
where the summation extends over all one-to-one functions
 from
from 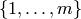 to
to
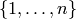 .
.
The product
 is
called diagonal product. So the permanent of an
is
called diagonal product. So the permanent of an
 matrix
matrix  is the sum of all the
diagonal products of
is the sum of all the
diagonal products of  .
.
Modification of theorem 7.1.1. from Brualdi and Ryser:
Combinatorial Matrix Theory. Instead of deleting columns from
 , we choose columns from
, we choose columns from  and calculate the
product of the row sums of the selected submatrix.
and calculate the
product of the row sums of the selected submatrix.
INPUT:
OUTPUT: permanent of matrix A
EXAMPLES:
sage: M = MatrixSpace(ZZ,4,4)
sage: A = M([1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1])
sage: A.permanent()
24
sage: M = MatrixSpace(QQ,3,6)
sage: A = M([1,1,1,1,0,0,0,1,1,1,1,0,0,0,1,1,1,1])
sage: A.permanent()
36
sage: M = MatrixSpace(RR,3,6)
sage: A = M([1.0,1.0,1.0,1.0,0,0,0,1.0,1.0,1.0,1.0,0,0,0,1.0,1.0,1.0,1.0])
sage: A.permanent()
36.0000000000000
See Sloane’s sequence OEIS A079908(3) = 36, “The Dancing School Problems”
sage: print sloane_sequence(79908) # optional (internet connection)
Searching Sloane's online database...
[79908, 'Solution to the Dancing School Problem with 3 girls and n+3 boys: f(3,n).', [1, 4, 14, 36, 76, 140, 234, 364, 536, 756, 1030, 1364, 1764, 2236, 2786, 3420, 4144, 4964, 5886, 6916, 8060, 9324, 10714, 12236, 13896, 15700, 17654, 19764, 22036, 24476, 27090, 29884, 32864, 36036, 39406, 42980, 46764, 50764, 54986, 59436]]
sage: M = MatrixSpace(ZZ,4,5)
sage: A = M([1,1,0,1,1,0,1,1,1,1,1,0,1,0,1,1,1,0,1,0])
sage: A.permanent()
32
See Minc: Permanents, Example 2.1, p. 5.
sage: M = MatrixSpace(QQ,2,2)
sage: A = M([1/5,2/7,3/2,4/5])
sage: A.permanent()
103/175
sage: R.<a> = PolynomialRing(ZZ)
sage: A = MatrixSpace(R,2)([[a,1], [a,a+1]])
sage: A.permanent()
a^2 + 2*a
sage: R.<x,y> = PolynomialRing(ZZ,2)
sage: A = MatrixSpace(R,2)([x, y, x^2, y^2])
sage: A.permanent()
x^2*y + x*y^2
AUTHORS:
Calculates the permanental  -minor of a
-minor of a
 matrix.
matrix.
This is the sum of the permanents of all possible  by
by
 submatrices of
submatrices of  .
.
See Brualdi and Ryser: Combinatorial Matrix Theory, p. 203. Note
the typo  in that reference! For applications
see Theorem 7.2.1 and Theorem 7.2.4.
in that reference! For applications
see Theorem 7.2.1 and Theorem 7.2.4.
Note that the permanental 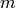 -minor equals
-minor equals
 .
.
For a (0,1)-matrix  the permanental
the permanental  -minor
counts the number of different selections of
-minor
counts the number of different selections of  1’s of
1’s of
 with no two of the 1’s on the same line.
with no two of the 1’s on the same line.
INPUT:
OUTPUT: permanental k-minor of matrix A
EXAMPLES:
sage: M = MatrixSpace(ZZ,4,4)
sage: A = M([1,0,1,0,1,0,1,0,1,0,10,10,1,0,1,1])
sage: A.permanental_minor(2)
114
sage: M = MatrixSpace(ZZ,3,6)
sage: A = M([1,1,1,1,0,0,0,1,1,1,1,0,0,0,1,1,1,1])
sage: A.permanental_minor(0)
1
sage: A.permanental_minor(1)
12
sage: A.permanental_minor(2)
40
sage: A.permanental_minor(3)
36
Note that if k == m the permanental k-minor equals per(A)
sage: A.permanent()
36
sage: A.permanental_minor(5)
0
For C the “complement” of A:
sage: M = MatrixSpace(ZZ,3,6)
sage: C = M([0,0,0,0,1,1,1,0,0,0,0,1,1,1,0,0,0,0])
sage: m, n = 3, 6
sage: sum([(-1)^k * C.permanental_minor(k)*factorial(n-k)/factorial(n-m) for k in range(m+1)])
36
See Theorem 7.2.1 of Brualdi: and Ryser: Combinatorial Matrix Theory: per(A)
AUTHORS:
Return the pivot row positions for this matrix, which are a topmost subset of the rows that span the row space and are linearly independent.
OUTPUT:
EXAMPLES:
sage: A = matrix(QQ,3,3, [0,0,0,1,2,3,2,4,6]); A
[0 0 0]
[1 2 3]
[2 4 6]
sage: A.pivot_rows()
[1]
A plot of this matrix.
Each (ith, jth) matrix element is given a different color value depending on its relative size compared to the other elements in the matrix.
The tick marks drawn on the frame axes denote the (ith, jth) element of the matrix.
This method just calls matrix_plot. *args and **kwds are passed to matrix_plot.
EXAMPLES:
A matrix over ZZ colored with different grey levels:
sage: A = matrix([[1,3,5,1],[2,4,5,6],[1,3,5,7]])
sage: A.plot()
Here we make a random matrix over RR and use cmap=’hsv’ to color the matrix elements different RGB colors (see documentation for matrix_plot for more information on cmaps):
sage: A = random_matrix(RDF, 50)
sage: plot(A, cmap='hsv')
Another random plot, but over GF(389):
sage: A = random_matrix(GF(389), 10)
sage: A.plot(cmap='Oranges')
Calculate the product of all row sums of a submatrix of  for a list of selected columns cols.
for a list of selected columns cols.
EXAMPLES:
sage: a = matrix(QQ, 2,2, [1,2,3,2]); a
[1 2]
[3 2]
sage: a.prod_of_row_sums([0,1])
15
Another example:
sage: a = matrix(QQ, 2,3, [1,2,3,2,5,6]); a
[1 2 3]
[2 5 6]
sage: a.prod_of_row_sums([1,2])
55
AUTHORS:
Randomize density proportion of the entries of this matrix, leaving the rest unchanged.
Note
We actually choose at random density proportion of entries of the matrix and set them to random elements. It’s possible that the same position can be chosen multiple times, especially for a very small matrix.
INPUT:
EXAMPLES:
We construct the zero matrix over a polynomial ring.
sage: a = matrix(QQ['x'], 3); a
[0 0 0]
[0 0 0]
[0 0 0]
We then randomize roughly half the entries:
sage: a.randomize(0.5)
sage: a
[ 1/2*x^2 - x - 12 1/2*x^2 - 1/95*x - 1/2 0]
[-5/2*x^2 + 2/3*x - 1/4 0 0]
[ -x^2 + 2/3*x 0 0]
Now we randomize all the entries of the resulting matrix:
sage: a.randomize()
sage: a
[ 1/3*x^2 - x + 1 -x^2 + 1 x^2 - x]
[ -1/14*x^2 - x - 1/4 -4*x - 1/5 -1/4*x^2 - 1/2*x + 4]
[ 1/9*x^2 + 5/2*x - 3 -x^2 + 3/2*x + 1 -2/7*x^2 - x - 1/2]
We create the zero matrix over the integers:
sage: a = matrix(ZZ, 2); a
[0 0]
[0 0]
Then we randomize it; the x and y parameters, which determine the size of the random elements, are passed onto the ZZ random_element method.
sage: a.randomize(x=-2^64, y=2^64)
sage: a
[-12401200298100116246 1709403521783430739]
[ -4417091203680573707 17094769731745295000]
Returns the matrix that defines the action of self on the chosen basis for the invariant subspace V. If V is an ambient, returns self (not a copy of self).
INPUT:
OUTPUT: a matrix
Warning
This function returns an nxn matrix, where V has dimension n. It does not check that V is in fact invariant under self, unless check is True.
EXAMPLES:
sage: V = VectorSpace(QQ, 3)
sage: M = MatrixSpace(QQ, 3)
sage: A = M([1,2,0, 3,4,0, 0,0,0])
sage: W = V.subspace([[1,0,0], [0,1,0]])
sage: A.restrict(W)
[1 2]
[3 4]
sage: A.restrict(W, check=True)
[1 2]
[3 4]
We illustrate the warning about invariance not being checked by default, by giving a non-invariant subspace. With the default check=False this function returns the ‘restriction’ matrix, which is meaningless as check=True reveals.
sage: W2 = V.subspace([[1,0,0], [0,1,1]])
sage: A.restrict(W2, check=False)
[1 2]
[3 4]
sage: A.restrict(W2, check=True)
...
ArithmeticError: subspace is not invariant under matrix
Suppose that self defines a linear map from some domain to a
codomain that contains 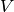 and that the image of self is
contained in
and that the image of self is
contained in 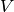 . This function returns a new matrix
. This function returns a new matrix
 that represents this linear map but as a map to
that represents this linear map but as a map to
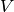 , in the sense that if
, in the sense that if  is in the domain,
then
is in the domain,
then 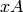 is the linear combination of the elements of the
basis of
is the linear combination of the elements of the
basis of 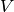 that equals v*self.
that equals v*self.
INPUT:
See also
EXAMPLES:
sage: A = matrix(QQ,3,[1..9])
sage: V = (QQ^3).span([[1,2,3], [7,8,9]]); V
Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[ 1 0 -1]
[ 0 1 2]
sage: z = vector(QQ,[1,2,5])
sage: B = A.restrict_codomain(V); B
[1 2]
[4 5]
[7 8]
sage: z*B
(44, 52)
sage: z*A
(44, 52, 60)
sage: 44*V.0 + 52*V.1
(44, 52, 60)
Compute the matrix relative to the basis for V on the domain obtained by restricting self to V, but not changing the codomain of the matrix. This is the matrix whose rows are the images of the basis for V.
INPUT:
See also
EXAMPLES:
sage: V = QQ^3
sage: A = matrix(QQ,3,[1,2,0, 3,4,0, 0,0,0])
sage: W = V.subspace([[1,0,0], [1,2,3]])
sage: A.restrict_domain(W)
[1 2 0]
[3 4 0]
sage: W2 = V.subspace_with_basis([[1,0,0], [1,2,3]])
sage: A.restrict_domain(W2)
[ 1 2 0]
[ 7 10 0]
Return matrices D and P, where D is a diagonal matrix of eigenvalues and P is the corresponding matrix where the columns are corresponding eigenvectors (or zero vectors) so that self*P = P*D.
EXAMPLES:
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: D, P = A.eigenmatrix_right()
sage: D
[ 0 0 0]
[ 0 -1.348469228349535? 0]
[ 0 0 13.34846922834954?]
sage: P
[ 1 1 1]
[ -2 0.1303061543300932? 3.069693845669907?]
[ 1 -0.7393876913398137? 5.139387691339814?]
sage: A*P == P*D
True
Because P is invertible, A is diagonalizable.
sage: A == P*D*(~P)
True
The matrix P may contain zero columns corresponding to eigenvalues for which the algebraic multiplicity is greater than the geometric multiplicity. In these cases, the matrix is not diagonalizable.
sage: A = jordan_block(2,3); A
[2 1 0]
[0 2 1]
[0 0 2]
sage: A = jordan_block(2,3)
sage: D, P = A.eigenmatrix_right()
sage: D
[2 0 0]
[0 2 0]
[0 0 2]
sage: P
[1 0 0]
[0 0 0]
[0 0 0]
sage: A*P == P*D
True
Compute right eigenspaces of a matrix.
If algebraic_multiplicity=False, return a list of pairs (e, V) where e runs through all eigenvalues (up to Galois conjugation) of this matrix, and V is the corresponding right eigenspace.
If algebraic_multiplicity=True, return a list of pairs (e, V, n) where e and V are as above and n is the algebraic multiplicity of the eigenvalue. If the eigenvalues are given symbolically, as roots of an irreducible factor of the characteristic polynomial, then the algebraic multiplicity returned is the multiplicity of each conjugate eigenvalue.
The eigenspaces are returned sorted by the corresponding characteristic polynomials, where polynomials are sorted in dictionary order starting with constant terms.
INPUT:
Warning
Uses a somewhat naive algorithm (simply factors the characteristic polynomial and computes kernels directly over the extension field).
TODO: Maybe implement the better algorithm that is in dual_eigenvector in sage/modular/hecke/module.py.
EXAMPLES: We compute the right eigenspaces of a  rational matrix.
rational matrix.
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: es = A.eigenspaces_right(); es
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1]),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/5*a1 + 2/5 2/5*a1 - 1/5])
]
sage: es = A.eigenspaces_right(algebraic_multiplicity=True); es
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1], 1),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/5*a1 + 2/5 2/5*a1 - 1/5], 1)
]
sage: e, v, n = es[0]; v = v.basis()[0]
sage: delta = v*e - A*v
sage: abs(abs(delta)) < 1e-10
True
The same computation, but with implicit base change to a field:
sage: A = matrix(ZZ,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: A.eigenspaces_right()
[
(0, Vector space of degree 3 and dimension 1 over Rational Field
User basis matrix:
[ 1 -2 1]),
(a1, Vector space of degree 3 and dimension 1 over Number Field in a1 with defining polynomial x^2 - 12*x - 18
User basis matrix:
[ 1 1/5*a1 + 2/5 2/5*a1 - 1/5])
]
TESTS: Warnings are issued if the generic algorithm is used over inexact fields. Garbage may result in these cases because of numerical precision issues.
sage: R=RealField(30)
sage: M=matrix(R,2,[2,1,1,1])
sage: M.eigenspaces_right() # random output from numerical issues
[(2.6180340,
Vector space of degree 2 and dimension 0 over Real Field with 30 bits of precision
User basis matrix:
[]),
(0.38196601,
Vector space of degree 2 and dimension 0 over Real Field with 30 bits of precision
User basis matrix:
[])]
sage: R=ComplexField(30)
sage: N=matrix(R,2,[2,1,1,1])
sage: N.eigenspaces_right() # random output from numerical issues
[(2.6180340,
Vector space of degree 2 and dimension 0 over Complex Field with 30 bits of precision
User basis matrix:
[]),
(0.38196601,
Vector space of degree 2 and dimension 0 over Complex Field with 30 bits of precision
User basis matrix:
[])]
Compute the right eigenvectors of a matrix.
For each distinct eigenvalue, returns a list of the form (e,V,n) where e is the eigenvalue, V is a list of eigenvectors forming a basis for the corresponding right eigenspace, and n is the algebraic multiplicity of the eigenvalue.
EXAMPLES: We compute the right eigenvectors of a
 rational matrix.
rational matrix.
sage: A = matrix(QQ,3,3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: es = A.eigenvectors_right(); es
[(0, [
(1, -2, 1)
], 1),
(-1.348469228349535?, [(1, 0.1303061543300932?, -0.7393876913398137?)], 1),
(13.34846922834954?, [(1, 3.069693845669907?, 5.139387691339814?)], 1)]
sage: eval, [evec], mult = es[0]
sage: delta = eval*evec - A*evec
sage: abs(abs(delta)) < 1e-10
True
Return the right kernel of this matrix, as a vector space. This is the space of vectors x such that self*x=0. A left kernel can be found with self.left_kernel() or just self.kernel().
INPUT: all additional arguments to the kernel function are passed directly onto the echelon call.
By convention if self has 0 columns, the kernel is of dimension 0, whereas the kernel is whole domain if self has 0 rows.
ALGORITHM:
Elementary row operations do not change the right kernel, since they are left multiplication by an invertible matrix, so we instead compute the kernel of the row echelon form. When the base ring is a field, then there is a basis vector of the kernel that corresponds to each non-pivot column. That vector has a 1 at the non-pivot column, 0’s at all other non-pivot columns, and for each pivot column, the negative of the entry at the non-pivot column in the row with that pivot element.
Over a non-field base ring, we still have a version of echelon form – Hermite normal form – but the above does not work, since the pivot entries might not be 1. Hence if the base ring is a PID, we use the Smith normal form of the matrix.
Note
Preference is given to left kernels in that the generic method name kernel() returns a left kernel. However most computations of kernels are implemented as right kernels.
EXAMPLES:
A right kernel of dimension one over  :
:
sage: A = MatrixSpace(QQ, 3)(range(9))
sage: A.right_kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2 1]
A trivial right kernel:
sage: A = MatrixSpace(QQ, 2)([1,2,3,4])
sage: A.right_kernel()
Vector space of degree 2 and dimension 0 over Rational Field
Basis matrix:
[]
Right kernel of a zero matrix:
sage: A = MatrixSpace(QQ, 2)(0)
sage: A.right_kernel()
Vector space of degree 2 and dimension 2 over Rational Field
Basis matrix:
[1 0]
[0 1]
Right kernel of a non-square matrix:
sage: A = MatrixSpace(QQ,2,3)(range(6))
sage: A.right_kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 -2 1]
The 2-dimensional right kernel of a matrix over a cyclotomic field:
sage: K = CyclotomicField(12); a=K.0
sage: M = MatrixSpace(K,2,4)([1,-1, 0,-2, 0,-a**2-1, 0,a**2-1])
sage: M
[ 1 -1 0 -2]
[ 0 -zeta12^2 - 1 0 zeta12^2 - 1]
sage: M.right_kernel()
Vector space of degree 4 and dimension 2 over Cyclotomic Field of order 12 and degree 4
Basis matrix:
[ 1 4/13*zeta12^2 - 1/13 0 -2/13*zeta12^2 + 7/13]
[ 0 0 1 0]
A nontrivial right kernel over a complicated base field.
sage: K = FractionField(PolynomialRing(QQ, 2, 'x'))
sage: M = MatrixSpace(K, 2)([[K.1, K.0], [K.1, K.0]])
sage: M
[x1 x0]
[x1 x0]
sage: M.right_kernel()
Vector space of degree 2 and dimension 1 over Fraction Field of Multivariate Polynomial Ring in x0, x1 over Rational Field
Basis matrix:
[ 1 x1/(-x0)]
Right kernel of a large dense rational matrix, which will invoke the fast IML routines in matrix_integer_dense class. Timing on a 64-bit 3 GHz dual-core machine is about 3 seconds to setup and about 1 second for the kernel() call. Timings that are one or two orders of magnitude larger indicate problems with reaching specialized derived classes.
sage: entries = [[1/(i+j+1) for i in srange(500)] for j in srange(500)]
sage: a = matrix(QQ, entries)
sage: a.right_kernel()
Vector space of degree 500 and dimension 0 over Rational Field
Basis matrix:
0 x 500 dense matrix over Rational Field
Right kernel of a matrix defined over a principal ideal domain which is not ZZ or a field. This invokes the general Smith normal form routine, rather than echelon form which is less suitable in this case.
sage: L.<w> = NumberField(x^2 - x + 2)
sage: OL = L.ring_of_integers()
sage: m = matrix(OL, [2, w])
sage: m.right_kernel()
Free module of degree 2 and rank 1 over Maximal Order in Number Field in w with defining polynomial x^2 - x + 2
Echelon basis matrix:
[ -1 -w + 1]
With zero columns the right kernel has dimension 0.
sage: M = matrix(QQ, [[],[],[]])
sage: M.right_kernel()
Vector space of degree 0 and dimension 0 over Rational Field
Basis matrix:
[]
With zero rows, the whole domain is the kernel, so the dimension is the number of columns.
sage: M = matrix(QQ, [[],[],[]]).transpose()
sage: M.right_kernel()
Vector space of dimension 3 over Rational Field
Return the right nullity of this matrix, which is the dimension of the right kernel.
EXAMPLES:
sage: A = MatrixSpace(QQ,3,2)(range(6))
sage: A.right_nullity()
0
sage: A = matrix(ZZ,3,range(9))
sage: A.right_nullity()
1
Returns rook vector of this matrix.
Let  be a general
be a general 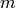 by
by  (0,1)-matrix with
(0,1)-matrix with 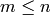 . We identify
. We identify  with a
chessboard where rooks can be placed on the fields corresponding
with
with a
chessboard where rooks can be placed on the fields corresponding
with 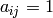 . The number
. The number
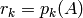 (the permanental
(the permanental
 -minor) counts the number of ways to place
-minor) counts the number of ways to place  rooks on this board so that no two rooks can attack another.
rooks on this board so that no two rooks can attack another.
The rook vector is the list consisting of
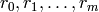 .
.
The rook polynomial is defined by
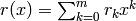 .
.
INPUT:
OUTPUT: rook vector
EXAMPLES:
sage: M = MatrixSpace(ZZ,3,6)
sage: A = M([1,1,1,1,0,0,0,1,1,1,1,0,0,0,1,1,1,1])
sage: A.rook_vector()
[1, 12, 40, 36]
sage: R.<x> = PolynomialRing(ZZ)
sage: rv = A.rook_vector()
sage: rook_polynomial = sum([rv[k] * x^k for k in range(len(rv))])
sage: rook_polynomial
36*x^3 + 40*x^2 + 12*x + 1
AUTHORS:
Return the free module over the base ring spanned by the rows of self.
EXAMPLES:
sage: A = MatrixSpace(IntegerRing(), 2)([1,2,3,4])
sage: A.row_module()
Free module of degree 2 and rank 2 over Integer Ring
Echelon basis matrix:
[1 0]
[0 2]
Return the row space of this matrix. (Synonym for self.row_module().)
EXAMPLES:
sage: t = matrix(QQ, 3, range(9)); t
[0 1 2]
[3 4 5]
[6 7 8]
sage: t.row_space()
Vector space of degree 3 and dimension 2 over Rational Field
Basis matrix:
[ 1 0 -1]
[ 0 1 2]
sage: m = Matrix(Integers(5),2,2,[2,2,2,2]);
sage: m.row_space()
Vector space of degree 2 and dimension 1 over Ring of integers modulo 5
Basis matrix:
[1 1]
Return the reduced row echelon form of the matrix, considered as a matrix over a field.
If the matrix is over a ring, then an equivalent matrix is constructed over the fraction field, and then row reduced.
All arguments are passed on to :meth:echelon_form.
Note
Because the matrix is viewed as a matrix over a field, every leading coefficient of the returned matrix will be one and will be the only nonzero entry in its column.
EXAMPLES:
sage: A=matrix(3,range(9)); A
[0 1 2]
[3 4 5]
[6 7 8]
sage: A.rref()
[ 1 0 -1]
[ 0 1 2]
[ 0 0 0]
Note that there is a difference between rref() and echelon_form() when the matrix is not over a field (in this case, the integers instead of the rational numbers):
sage: A.base_ring()
Integer Ring
sage: A.echelon_form()
[ 3 0 -3]
[ 0 1 2]
[ 0 0 0]
sage: B=random_matrix(QQ,3,num_bound=10); B
[ -4 -3 6]
[ 5 -5 9/2]
[3/2 -4 -7]
sage: B.rref()
[1 0 0]
[0 1 0]
[0 0 1]
In this case, since B is a matrix over a field (the rational numbers), rref() and echelon_form() are exactly the same:
sage: B.echelon_form()
[1 0 0]
[0 1 0]
[0 0 1]
sage: B.echelon_form() is B.rref()
True
Since echelon_form() is not implemented for every ring, sometimes behavior varies, as here:
sage: R.<x>=ZZ[]
sage: C = matrix(3,[2,x,x^2,x+1,3-x,-1,3,2,1])
sage: C.rref()
[1 0 0]
[0 1 0]
[0 0 1]
sage: C.base_ring()
Univariate Polynomial Ring in x over Integer Ring
sage: C.echelon_form()
...
NotImplementedError: Echelon form not implemented over 'Univariate Polynomial Ring in x over Integer Ring'.
sage: C = matrix(3,[2,x,x^2,x+1,3-x,-1,3,2,1/2])
sage: C.echelon_form()
[ 2 x x^2]
[ 0 1 15*x^2 - 3/2*x - 31/2]
[ 0 0 5/2*x^3 - 15/4*x^2 - 9/4*x + 7/2]
sage: C.rref()
[1 0 0]
[0 1 0]
[0 0 1]
sage: C = matrix(3,[2,x,x^2,x+1,3-x,-1/x,3,2,1/2])
sage: C.echelon_form()
[1 0 0]
[0 1 0]
[0 0 1]
Sets the sub-matrix of self, with upper left corner given by row, col to block.
EXAMPLES:
sage: A = matrix(QQ, 3, 3, range(9))/2
sage: B = matrix(ZZ, 2, 1, [100,200])
sage: A.set_block(0, 1, B)
sage: A
[ 0 100 1]
[3/2 200 5/2]
[ 3 7/2 4]
We test that an exception is raised when the block is out of bounds:
sage: matrix([1]).set_block(0,1,matrix([1]))
...
IndexError: matrix window index out of range
If self is a matrix over a principal ideal domain R, return
matrices D, U, V over R such that D = U * self * V, U and V have
unit determinant, and D is diagonal with diagonal entries the
ordered elementary divisors of self, ordered so that
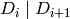 . Note that U and V are not uniquely
defined in general, and D is defined only up to units.
. Note that U and V are not uniquely
defined in general, and D is defined only up to units.
INPUT:
ALGORITHM: Lifted wholesale from http://en.wikipedia.org/wiki/Smith_normal_form
See also
AUTHORS:
EXAMPLES:
An example over the ring of integers of a number field (of class number 1):
sage: OE = NumberField(x^2 - x + 2,'w').ring_of_integers()
sage: w = OE.ring_generators()[0]
sage: m = Matrix([ [1, w],[w,7]])
sage: d, u, v = m.smith_form()
sage: (d, u, v)
(
[ 1 0] [ 1 0] [ 1 -w]
[ 0 -w + 9], [-w 1], [ 0 1]
)
sage: u * m * v == d
True
sage: u.base_ring() == v.base_ring() == d.base_ring() == OE
True
sage: u.det().is_unit() and v.det().is_unit()
True
An example over the polynomial ring QQ[x]:
sage: R.<x> = QQ[]; m=x*matrix(R,2,2,1) - matrix(R, 2,2,[3,-4,1,-1]); m.smith_form()
(
[ 1 0] [ 0 -1] [ 1 x + 1]
[ 0 x^2 - 2*x + 1], [ 1 x - 3], [ 0 1]
)
An example over a field:
sage: m = matrix( GF(17), 3, 3, [11,5,1,3,6,8,1,16,0]); d,u,v = m.smith_form()
sage: d
[1 0 0]
[0 1 0]
[0 0 0]
sage: u*m*v == d
True
Some examples over non-PID’s work anyway:
sage: R = EquationOrder(x^2 + 5, 's') # class number 2
sage: s = R.ring_generators()[0]
sage: matrix(R, 2, 2, [s-1,-s,-s,2*s+1]).smith_form()
(
[ 1 0] [ -1 -1] [ 1 s + 1]
[ 0 -s - 6], [ s s - 1], [ 0 1]
)
Others don’t, but they fail quite constructively:
sage: matrix(R,2,2,[s-1,-s-2,-2*s,-s-2]).smith_form()
...
ArithmeticError: Ideal Fractional ideal (2, s + 1) not principal
Empty matrices are handled safely:
sage: m = MatrixSpace(OE, 2,0)(0); d,u,v=m.smith_form(); u*m*v == d
True
sage: m = MatrixSpace(OE, 0,2)(0); d,u,v=m.smith_form(); u*m*v == d
True
sage: m = MatrixSpace(OE, 0,0)(0); d,u,v=m.smith_form(); u*m*v == d
True
Some pathological cases that crashed earlier versions:
sage: m = Matrix(OE, [[2*w,2*w-1,-w+1],[2*w+2,-2*w-1,w-1],[-2*w-1,-2*w-2,2*w-1]]); d, u, v = m.smith_form(); u * m * v == d
True
sage: m = matrix(OE, 3, 3, [-5*w-1,-2*w-2,4*w-10,8*w,-w,w-1,-1,1,-8]); d,u,v = m.smith_form(); u*m*v == d
True
If self is a matrix  , then this function returns a
vector or matrix
, then this function returns a
vector or matrix  such that
such that 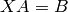 . If
. If
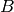 is a vector then
is a vector then  is a vector and if
is a vector and if
 is a matrix, then
is a matrix, then  is a matrix.
is a matrix.
INPUT:
EXAMPLES:
sage: A = matrix(QQ,4,2, [0, -1, 1, 0, -2, 2, 1, 0])
sage: B = matrix(QQ,2,2, [1, 0, 1, -1])
sage: X = A.solve_left(B)
sage: X*A == B
True
TESTS:
sage: A = matrix(QQ,4,2, [0, -1, 1, 0, -2, 2, 1, 0])
sage: B = vector(QQ,2, [2,1])
sage: X = A.solve_left(B)
sage: X*A == B
True
sage: X
(-1, 2, 0, 0)
If self is a matrix  , then this function returns a
vector or matrix
, then this function returns a
vector or matrix  such that
such that  . If
. If
 is a vector then
is a vector then  is a vector and if
is a vector and if
 is a matrix, then
is a matrix, then  is a matrix.
is a matrix.
Note
In Sage one can also write A \backslash B for A.solve_right(B), i.e., Sage implements the “the MATLAB/Octave backslash operator”.
INPUT:
OUTPUT: a matrix or vector
See also
EXAMPLES:
sage: A = matrix(QQ, 3, [1,2,3,-1,2,5,2,3,1])
sage: b = vector(QQ,[1,2,3])
sage: x = A \ b; x
(-13/12, 23/12, -7/12)
sage: A * x
(1, 2, 3)
We solve with A nonsquare:
sage: A = matrix(QQ,2,4, [0, -1, 1, 0, -2, 2, 1, 0]); B = matrix(QQ,2,2, [1, 0, 1, -1])
sage: X = A.solve_right(B); X
[-3/2 1/2]
[ -1 0]
[ 0 0]
[ 0 0]
sage: A*X == B
True
Another nonsingular example:
sage: A = matrix(QQ,2,3, [1,2,3,2,4,6]); v = vector([-1/2,-1])
sage: x = A \ v; x
(-1/2, 0, 0)
sage: A*x == v
True
Same example but over  :
:
sage: A = matrix(ZZ,2,3, [1,2,3,2,4,6]); v = vector([-1,-2])
sage: A \ v
(-1, 0, 0)
An example in which there is no solution:
sage: A = matrix(QQ,2,3, [1,2,3,2,4,6]); v = vector([1,1])
sage: A \ v
...
ValueError: matrix equation has no solutions
A ValueError is raised if the input is invalid:
sage: A = matrix(QQ,4,2, [0, -1, 1, 0, -2, 2, 1, 0])
sage: B = matrix(QQ,2,2, [1, 0, 1, -1])
sage: X = A.solve_right(B)
...
ValueError: number of rows of self must equal number of rows of B
We solve with A singular:
sage: A = matrix(QQ,2,3, [1,2,3,2,4,6]); B = matrix(QQ,2,2, [6, -6, 12, -12])
sage: X = A.solve_right(B); X
[ 6 -6]
[ 0 0]
[ 0 0]
sage: A*X == B
True
We illustrate left associativity, etc., of the backslash operator.
sage: A = matrix(QQ, 2, [1,2,3,4])
sage: A \ A
[1 0]
[0 1]
sage: A \ A \ A
[1 2]
[3 4]
sage: A.parent()(1) \ A
[1 2]
[3 4]
sage: A \ (A \ A)
[ -2 1]
[ 3/2 -1/2]
sage: X = A \ (A - 2); X
[ 5 -2]
[-3 2]
sage: A * X
[-1 2]
[ 3 2]
Solving over a polynomial ring:
sage: x = polygen(QQ, 'x')
sage: A = matrix(2, [x,2*x,-5*x^2+1,3])
sage: v = vector([3,4*x - 2])
sage: X = A \ v
sage: X
((-8*x^2 + 4*x + 9)/(10*x^3 + x), (19*x^2 - 2*x - 3)/(10*x^3 + x))
sage: A * X == v
True
Solving a system over the p-adics:
sage: k = Qp(5,4)
sage: a = matrix(k, 3, [1,7,3,2,5,4,1,1,2]); a
[ 1 + O(5^4) 2 + 5 + O(5^4) 3 + O(5^4)]
[ 2 + O(5^4) 5 + O(5^5) 4 + O(5^4)]
[ 1 + O(5^4) 1 + O(5^4) 2 + O(5^4)]
sage: v = vector(k, 3, [1,2,3])
sage: x = a \ v; x
(4 + 5 + 5^2 + 3*5^3 + O(5^4), 2 + 5 + 3*5^2 + 5^3 + O(5^4), 1 + 5 + O(5^4))
sage: a * x == v
True
Divides self into logical submatrices which can then be queried and extracted. If a subdivision already exists, this method forgets the previous subdivision and flushes the cache.
INPUT:
OUTPUT: changes self
Note
One may also pass a tuple into the first argument which will be interpreted as (row_lines, col_lines)
EXAMPLES:
sage: M = matrix(5, 5, prime_range(100))
sage: M.subdivide(2,3); M
[ 2 3 5| 7 11]
[13 17 19|23 29]
[--------+-----]
[31 37 41|43 47]
[53 59 61|67 71]
[73 79 83|89 97]
sage: M.subdivision(0,0)
[ 2 3 5]
[13 17 19]
sage: M.subdivision(1,0)
[31 37 41]
[53 59 61]
[73 79 83]
sage: M.subdivision_entry(1,0,0,0)
31
sage: M.get_subdivisions()
([2], [3])
sage: M.subdivide(None, [1,3]); M
[ 2| 3 5| 7 11]
[13|17 19|23 29]
[31|37 41|43 47]
[53|59 61|67 71]
[73|79 83|89 97]
Degenerate cases work too.
sage: M.subdivide([2,5], [0,1,3]); M
[| 2| 3 5| 7 11]
[|13|17 19|23 29]
[+--+-----+-----]
[|31|37 41|43 47]
[|53|59 61|67 71]
[|73|79 83|89 97]
[+--+-----+-----]
sage: M.subdivision(0,0)
[]
sage: M.subdivision(0,1)
[ 2]
[13]
sage: M.subdivide([2,2,3], [0,0,1,1]); M
[|| 2|| 3 5 7 11]
[||13||17 19 23 29]
[++--++-----------]
[++--++-----------]
[||31||37 41 43 47]
[++--++-----------]
[||53||59 61 67 71]
[||73||79 83 89 97]
sage: M.subdivision(0,0)
[]
sage: M.subdivision(2,4)
[37 41 43 47]
AUTHORS:
Returns in immutable copy of the (i,j)th submatrix of self, according to a previously set subdivision.
Before a subdivision is set, the only valid arguments are (0,0) which returns self.
EXAMPLE:
sage: M = matrix(3, 4, range(12))
sage: M.subdivide(1,2); M
[ 0 1| 2 3]
[-----+-----]
[ 4 5| 6 7]
[ 8 9|10 11]
sage: M.subdivision(0,0)
[0 1]
sage: M.subdivision(0,1)
[2 3]
sage: M.subdivision(1,0)
[4 5]
[8 9]
It handles size-zero subdivisions as well.
sage: M = matrix(3, 4, range(12))
sage: M.subdivide([0],[0,2,2,4]); M
[+-----++-----+]
[| 0 1|| 2 3|]
[| 4 5|| 6 7|]
[| 8 9||10 11|]
sage: M.subdivision(0,0)
[]
sage: M.subdivision(1,1)
[0 1]
[4 5]
[8 9]
sage: M.subdivision(1,2)
[]
sage: M.subdivision(1,0)
[]
sage: M.subdivision(0,1)
[]
Returns the x,y entry of the i,j submatrix of self.
EXAMPLES:
sage: M = matrix(5, 5, range(25))
sage: M.subdivide(3,3); M
[ 0 1 2| 3 4]
[ 5 6 7| 8 9]
[10 11 12|13 14]
[--------+-----]
[15 16 17|18 19]
[20 21 22|23 24]
sage: M.subdivision_entry(0,0,1,2)
7
sage: M.subdivision(0,0)[1,2]
7
sage: M.subdivision_entry(0,1,0,0)
3
sage: M.subdivision_entry(1,0,0,0)
15
sage: M.subdivision_entry(1,1,1,1)
24
Even though this entry exists in the matrix, the index is invalid for the submatrix.
sage: M.subdivision_entry(0,0,4,0)
...
IndexError: Submatrix 0,0 has no entry 4,0
EXAMPLES:
sage: var('a,b,d,e')
(a, b, d, e)
sage: m = matrix([[a,b], [d,e]])
sage: m.substitute(a=1)
[1 b]
[d e]
sage: m.subs(a=b, b=d)
[b d]
[d e]
Find a symplectic form for self if self is an anti-symmetric, alternating matrix defined over a field.
Returns a pair (F, C) such that the rows of C form a symplectic basis for self and F = C * self * C.transpose().
Raises a ValueError if not over a field, or self is not anti-symmetric, or self is not alternating.
Anti-symmetric means that 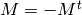 . Alternating means
that the diagonal of
. Alternating means
that the diagonal of  is identically zero.
is identically zero.
A symplectic basis is a basis of the form
 such that
such that
 = 0 for all vectors
= 0 for all vectors 
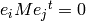 for all
for all 
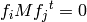 for all
for all 
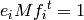 for all
for all 
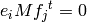 for all
for all  not equal
not equal
 .
.See the example for a pictorial description of such a basis.
EXAMPLES:
sage: E = matrix(QQ, 8, 8, [0, -1/2, -2, 1/2, 2, 0, -2, 1, 1/2, 0, -1, -3, 0, 2, 5/2, -3, 2, 1, 0, 3/2, -1, 0, -1, -2, -1/2, 3, -3/2, 0, 1, 3/2, -1/2, -1/2, -2, 0, 1, -1, 0, 0, 1, -1, 0, -2, 0, -3/2, 0, 0, 1/2, -2, 2, -5/2, 1, 1/2, -1, -1/2, 0, -1, -1, 3, 2, 1/2, 1, 2, 1, 0]); E
[ 0 -1/2 -2 1/2 2 0 -2 1]
[ 1/2 0 -1 -3 0 2 5/2 -3]
[ 2 1 0 3/2 -1 0 -1 -2]
[-1/2 3 -3/2 0 1 3/2 -1/2 -1/2]
[ -2 0 1 -1 0 0 1 -1]
[ 0 -2 0 -3/2 0 0 1/2 -2]
[ 2 -5/2 1 1/2 -1 -1/2 0 -1]
[ -1 3 2 1/2 1 2 1 0]
sage: F, C = E.symplectic_form(); F
[ 0 0 0 0 1 0 0 0]
[ 0 0 0 0 0 1 0 0]
[ 0 0 0 0 0 0 1 0]
[ 0 0 0 0 0 0 0 1]
[-1 0 0 0 0 0 0 0]
[ 0 -1 0 0 0 0 0 0]
[ 0 0 -1 0 0 0 0 0]
[ 0 0 0 -1 0 0 0 0]
sage: F == C * E * C.transpose()
True
Returns the tensor product of two matrices.
EXAMPLES:
sage: M1=Matrix(QQ,[[-1,0],[-1/2,-1]])
sage: M2=Matrix(ZZ,[[1,-1,2],[-2,4,8]])
sage: M1.tensor_product(M2)
[ -1 1 -2| 0 0 0]
[ 2 -4 -8| 0 0 0]
[--------------+--------------]
[-1/2 1/2 -1| -1 1 -2]
[ 1 -2 -4| 2 -4 -8]
sage: M2.tensor_product(M1)
[ -1 0| 1 0| -2 0]
[-1/2 -1| 1/2 1| -1 -2]
[---------+---------+---------]
[ 2 0| -4 0| -8 0]
[ 1 2| -2 -4| -4 -8]
Return the trace of self, which is the sum of the diagonal entries of self.
INPUT:
OUTPUT: element of the base ring of self
EXAMPLES:
sage: a = matrix(3,range(9)); a
[0 1 2]
[3 4 5]
[6 7 8]
sage: a.trace()
12
sage: a = matrix({(1,1):10, (2,1):-3, (2,2):4/3}); a
[ 0 0 0]
[ 0 10 0]
[ 0 -3 4/3]
sage: a.trace()
34/3
Returns the trace of self * other without computing the entire product.
EXAMPLES:
sage: M = random_matrix(ZZ, 10, 20)
sage: N = random_matrix(ZZ, 20, 10)
sage: M.trace_of_product(N)
5070
sage: (M*N).trace()
5070
Write a PNG image to ‘filename’ which visualizes self by putting black pixels in those positions which have nonzero entries.
White pixels are put at positions with zero entries. If ‘maxsize’ is given, then the maximal dimension in either x or y direction is set to ‘maxsize’ depending on which is bigger. If the image is scaled, the darkness of the pixel reflects how many of the represented entries are nonzero. So if e.g. one image pixel actually represents a 2x2 submatrix, the dot is darker the more of the four values are nonzero.
INPUT:
maxsize - maximal dimension in either x or y direction of the resulting image. If None or a maxsize larger than max(self.nrows(),self.ncols()) is given the image will have the same pixelsize as the matrix dimensions (default: 512)
EXAMPLE:
sage: M = random_matrix(CC, 4)
sage: M.visualize_structure(SAGE_TMP + "matrix.png")
Application of Wiedemann’s algorithm to the i-th standard basis vector.
INPUT:
IMPLEMENTATION: This is a toy implementation.
EXAMPLES:
sage: t = matrix(QQ, 3, range(9)); t
[0 1 2]
[3 4 5]
[6 7 8]
sage: t.wiedemann(0)
x^2 - 12*x - 18
sage: t.charpoly()
x^3 - 12*x^2 - 18*x
Compare two sequences of pivot columns.
This function is used internally be the decomposition matrix method. It takes a list of tuples and produces a sequence that is correctly sorted and prints with carriage returns.
EXAMPLES:
sage: from sage.matrix.matrix2 import decomp_seq
sage: V = [(QQ^3, 2), (QQ^2, 1)]
sage: decomp_seq(V)
[
(Vector space of dimension 2 over Rational Field, 1),
(Vector space of dimension 3 over Rational Field, 2)
]