Base class for matrices, part 0¶

Note

For design documentation see matrix/docs.py.

EXAMPLES:

sage: matrix(2,[1,2,3,4])
[1 2]
[3 4]

class sage.matrix.matrix0.Matrix¶

Bases: sage.structure.element.Matrix

A generic matrix.

The Matrix class is the base class for all matrix classes. To create a Matrix, first create a MatrixSpace, then coerce a list of elements into the MatrixSpace. See the documentation of MatrixSpace for more details.

EXAMPLES:

We illustrate matrices and matrix spaces. Note that no actual matrix that you make should have class Matrix; the class should always be derived from Matrix.

sage: M = MatrixSpace(CDF,2,3); M
Full MatrixSpace of 2 by 3 dense matrices over Complex Double Field
sage: a = M([1,2,3,  4,5,6]); a
[1.0 2.0 3.0]
[4.0 5.0 6.0]
sage: type(a)
<type 'sage.matrix.matrix_complex_double_dense.Matrix_complex_double_dense'>
sage: parent(a)
Full MatrixSpace of 2 by 3 dense matrices over Complex Double Field

sage: matrix(CDF, 2,3, [1,2,3, 4,5,6])
[1.0 2.0 3.0]
[4.0 5.0 6.0]
sage: Mat(CDF,2,3)(range(1,7))
[1.0 2.0 3.0]
[4.0 5.0 6.0]

sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -1,-1)
sage: matrix(Q,2,1,[1,2])
[1]
[2]

act_on_polynomial(f)¶

Returns the polynomial f(self*x).

INPUT:

self - an nxn matrix
f - a polynomial in n variables x=(x1,...,xn)

OUTPUT: The polynomial f(self*x).

EXAMPLES:

sage: R.<x,y> = QQ[]
sage: x, y = R.gens()
sage: f = x**2 - y**2
sage: M = MatrixSpace(QQ, 2)
sage: A = M([1,2,3,4])
sage: A.act_on_polynomial(f)
-8*x^2 - 20*x*y - 12*y^2

add_multiple_of_column(i, j, s, start_row=0)¶

Add s times column j to column i.

EXAMPLES: We add -1 times the third column to the second column of an integer matrix, remembering to start numbering cols at zero:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.add_multiple_of_column(1,2,-1)
sage: a
[ 0 -1  2]
[ 3 -1  5]           

To add a rational multiple, we first need to change the base ring:

sage: a = a.change_ring(QQ)
sage: a.add_multiple_of_column(1,0,1/3)
sage: a            
[ 0 -1  2]
[ 3  0  5]

If not, we get an error message:

sage: a.add_multiple_of_column(1,0,i)
...
TypeError: Multiplying column by Symbolic Ring element cannot be done over Rational Field, use change_ring or with_added_multiple_of_column instead.

add_multiple_of_row(i, j, s, start_col=0)¶

Add s times row j to row i.

EXAMPLES: We add -3 times the first row to the second row of an integer matrix, remembering to start numbering rows at zero:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]        
sage: a.add_multiple_of_row(1,0,-3)
sage: a
[ 0  1  2]
[ 3  1 -1]

To add a rational multiple, we first need to change the base ring:

sage: a = a.change_ring(QQ)
sage: a.add_multiple_of_row(1,0,1/3)
sage: a            
[   0    1    2]
[   3  4/3 -1/3]

If not, we get an error message:

sage: a.add_multiple_of_row(1,0,i)
...
TypeError: Multiplying row by Symbolic Ring element cannot be done over Rational Field, use change_ring or with_added_multiple_of_row instead.

base_ring()¶

change_ring(ring)¶

Return the matrix obtained by coercing the entries of this matrix into the given ring.

Always returns a copy (unless self is immutable, in which case returns self).

EXAMPLES:

sage: A = Matrix(QQ, 2, 2, [1/2, 1/3, 1/3, 1/4])
sage: A.parent()
 Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: A.change_ring(GF(25,'a'))
[3 2]
[2 4]
sage: A.change_ring(GF(25,'a')).parent()
 Full MatrixSpace of 2 by 2 dense matrices over Finite Field in a of size 5^2
sage: A.change_ring(ZZ)
...
TypeError: matrix has denominators so can't change to ZZ.

Changing rings preserves subdivisions:

sage: A.subdivide([1], []); A
[1/2 1/3]
[-------]
[1/3 1/4]
sage: A.change_ring(GF(25,'a'))
[3 2]
[---]
[2 4]

commutator(other)¶

Return the commutator self*other - other*self.

EXAMPLES:

sage: A = Matrix(ZZ, 2, 2, range(4))
sage: B = Matrix(ZZ, 2, 2, [0, 1, 0, 0])
sage: A.commutator(B)
[-2 -3]
[ 0  2]
sage: A.commutator(B) == -B.commutator(A)
True

copy()¶

Make a copy of self. If self is immutable, the copy will be mutable.

Warning

This method is deprecated and will be removed from a future version of Sage. Please use the copy() function instead. In other words, instead of doing m.copy(), do copy(m).

Warning

The individual elements aren’t themselves copied (though the list is copied). This shouldn’t matter, since ring elements are (almost!) always immutable in Sage.

EXAMPLES:

The copy() method is deprecated. Instead, use the copy() function:

sage: a = matrix([[1,2],[3,4]])
sage: b = a.copy()
doctest:...: DeprecationWarning: the .copy() method is deprecated; please use the copy() function instead, for example, copy(M)
sage: b = copy(a)

sage: R.<x> = QQ['x']
sage: a = matrix(R,2,[x+1,2/3,  x^2/2, 1+x^3]); a
[  x + 1     2/3]
[1/2*x^2 x^3 + 1]
sage: b = copy(a)
sage: b[0,0] = 5
sage: b
[      5     2/3]
[1/2*x^2 x^3 + 1]
sage: a
[  x + 1     2/3]
[1/2*x^2 x^3 + 1]

sage: b = copy(a)
sage: f = b[0,0]; f[0] = 10
...
IndexError: polynomials are immutable

dict()¶

Dictionary of the elements of self with keys pairs (i,j) and values the nonzero entries of self.

It is safe to change the returned dictionary.

EXAMPLES:

sage: R.<x,y> = QQ[]
sage: a = matrix(R,2,[x,y,0, 0,0,2*x+y]); a
[      x       y       0]
[      0       0 2*x + y]            
sage: d = a.dict(); d
{(0, 1): y, (1, 2): 2*x + y, (0, 0): x}

Notice that changing the returned list does not change a (the list is a copy):

sage: d[0,0] = 25
sage: a
[      x       y       0]
[      0       0 2*x + y]

is_dense()¶

Returns True if this is a dense matrix.

In Sage, being dense is a property of the underlying representation, not the number of nonzero entries.

EXAMPLES:

sage: matrix(QQ,2,2,range(4)).is_dense()
True
sage: matrix(QQ,2,2,range(4),sparse=True).is_dense()
False

is_immutable()¶

Return True if this matrix is immutable.

See the documentation for self.set_immutable for more details about mutability.

EXAMPLES:

sage: A = Matrix(QQ['t','s'], 2, 2, range(4))
sage: A.is_immutable()
False
sage: A.set_immutable()
sage: A.is_immutable()
True

is_invertible()¶

Return True if this matrix is invertible.

EXAMPLES: The following matrix is invertible over $\QQ$ but not over $\ZZ$ .

sage: A = MatrixSpace(ZZ, 2)(range(4))
sage: A.is_invertible()
False
sage: A.matrix_over_field().is_invertible()
True

The inverse function is a constructor for matrices over the fraction field, so it can work even if A is not invertible.

sage: ~A   # inverse of A
[-3/2  1/2]
[   1    0]

The next matrix is invertible over $\ZZ$ .

sage: A = MatrixSpace(IntegerRing(),2)([1,10,0,-1])
sage: A.is_invertible()
True
sage: ~A                # compute the inverse
[ 1 10]
[ 0 -1]

The following nontrivial matrix is invertible over $\ZZ[x]$ .

sage: R.<x> = PolynomialRing(IntegerRing())
sage: A = MatrixSpace(R,2)([1,x,0,-1])
sage: A.is_invertible()
True
sage: ~A
[ 1  x]
[ 0 -1]

is_mutable()¶

Return True if this matrix is mutable.

See the documentation for self.set_immutable for more details about mutability.

EXAMPLES:

sage: A = Matrix(QQ['t','s'], 2, 2, range(4))
sage: A.is_mutable()
True
sage: A.set_immutable()
sage: A.is_mutable()
False

is_skew_symmetric()¶

Returns True if this is a skew symmetric matrix.

EXAMPLES:

sage: m = matrix(QQ, [[0,2], [-2,0]])
sage: m.is_skew_symmetric()
True
sage: m = matrix(QQ, [[1,2], [2,1]])
sage: m.is_skew_symmetric()
False

is_sparse()¶

Return True if this is a sparse matrix.

In Sage, being sparse is a property of the underlying representation, not the number of nonzero entries.

EXAMPLES:

sage: matrix(QQ,2,2,range(4)).is_sparse()
False
sage: matrix(QQ,2,2,range(4),sparse=True).is_sparse()
True

is_square()¶

Return True precisely if this matrix is square, i.e., has the same number of rows and columns.

EXAMPLES:

sage: matrix(QQ,2,2,range(4)).is_square()
True
sage: matrix(QQ,2,3,range(6)).is_square()
False

is_symmetric()¶: Returns True if this is a symmetric matrix.

iterates(v, n, rows=True)¶

Let $A$ be this matrix and $v$ be a free module element. If rows is True, return a matrix whose rows are the entries of the following vectors:

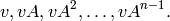
$v, v A, v A^2, \ldots, v A^{n-1}.$

If rows is False, return a matrix whose columns are the entries of the following vectors:

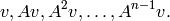
$v, Av, A^2 v, \ldots, A^{n-1} v.$

INPUT:

v - free module element
n - nonnegative integer

EXAMPLES:

sage: A = matrix(ZZ,2, [1,1,3,5]); A
[1 1]
[3 5]
sage: v = vector([1,0])
sage: A.iterates(v,0)
[]
sage: A.iterates(v,5)
[  1   0]
[  1   1]
[  4   6]
[ 22  34]
[124 192]

Another example:

sage: a = matrix(ZZ,3,range(9)); a
[0 1 2]
[3 4 5]
[6 7 8]
sage: v = vector([1,0,0])
sage: a.iterates(v,4)
[  1   0   0]
[  0   1   2]
[ 15  18  21]
[180 234 288]
sage: a.iterates(v,4,rows=False)
[  1   0  15 180]
[  0   3  42 558]
[  0   6  69 936]

linear_combination_of_columns(v)¶

Return the linear combination of the columns of self given by the coefficients in the list v. Raise a ValueError if the length of v is longer than the number of columns of the matrix.

INPUT:

v - list of length at most the number of columns of self (less is fine)

EXAMPLES:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.linear_combination_of_columns([1,1,1])
(3, 12)
sage: a.linear_combination_of_columns([0,0,0])
(0, 0)
sage: a.linear_combination_of_columns([1/2,2/3,3/4])
 (13/6, 95/12)
sage: matrix(QQ,2,0).linear_combination_of_columns([])
(0, 0)

The length of v can be less than the number of columns, but not more than the number of columns:

sage: A = matrix(QQ,2,3)
sage: A.linear_combination_of_columns([0])
(0, 0)
sage: A.linear_combination_of_columns([1,2,3,4])
...
ValueError: length of v must be at most the number of columns of self

linear_combination_of_rows(v)¶

Return the linear combination of the rows of self given by the coefficients in the list v. Raise a ValueError if the length of v is longer than the number of rows of the matrix.

INPUT:

v - list of length at most the number of rows of

self (less is fine)

EXAMPLES:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.linear_combination_of_rows([1,2])
(6, 9, 12)
sage: a.linear_combination_of_rows([0,0])
(0, 0, 0)
sage: a.linear_combination_of_rows([1/2,2/3])
(2, 19/6, 13/3)
sage: matrix(QQ,0,2).linear_combination_of_rows([])
(0, 0)

The length of v can be less than the number of rows, but not more than the number of rows:

sage: A = matrix(QQ,2,3)
sage: A.linear_combination_of_rows([0])
(0, 0, 0)
sage: A.linear_combination_of_rows([1,2,3])
...
ValueError: length of v must be at most the number of rows of self

list()¶

List of the elements of self ordered by elements in each row. It is safe to change the returned list.

Warning

This function returns a list of the entries in the matrix self. It does not return a list of the rows of self, so it is different than the output of list(self), which returns [self[0],self[1],...].

EXAMPLES:

sage: R.<x,y> = QQ[]
sage: a = matrix(R,2,[x,y,x*y, y,x,2*x+y]); a
[      x       y     x*y]
[      y       x 2*x + y]
sage: v = a.list(); v
[x, y, x*y, y, x, 2*x + y]

Note that list(a) is different than a.list():

sage: a.list()
[x, y, x*y, y, x, 2*x + y]
sage: list(a)
[(x, y, x*y), (y, x, 2*x + y)]

Notice that changing the returned list does not change a (the list is a copy):

sage: v[0] = 25
sage: a
[      x       y     x*y]
[      y       x 2*x + y]

mod(p)¶

Return matrix mod $p$ , over the reduced ring.

EXAMPLES:

sage: M = matrix(ZZ, 2, 2, [5, 9, 13, 15])
sage: M.mod(7)
[5 2]
[6 1]
sage: parent(M.mod(7))
Full MatrixSpace of 2 by 2 dense matrices over Ring of integers modulo 7

multiplicative_order()¶

Return the multiplicative order of this matrix, which must therefore be invertible.

EXAMPLES:

sage: A = matrix(GF(59),3,[10,56,39,53,56,33,58,24,55])
sage: A.multiplicative_order()
580
sage: (A^580).is_one()
True

sage: B = matrix(GF(10007^3,'b'),0)
sage: B.multiplicative_order()
1

sage: C = matrix(GF(2^10,'c'),2,3,[1]*6)
sage: C.multiplicative_order()
...
ArithmeticError: self must be invertible ...

sage: D = matrix(IntegerModRing(6),3,[5,5,3,0,2,5,5,4,0])
sage: D.multiplicative_order()
...
NotImplementedError: ... only ... over finite fields

sage: E = MatrixSpace(GF(11^2,'e'),5).random_element()
sage: (E^E.multiplicative_order()).is_one()
True

REFERENCES:

Frank Celler and C. R. Leedham-Green, “Calculating the Order of an Invertible Matrix”, 1997

ncols()¶

Return the number of columns of this matrix.

EXAMPLES:

sage: M = MatrixSpace(QQ, 2, 3)
sage: A = M([1,2,3, 4,5,6])
sage: A
[1 2 3]
[4 5 6]
sage: A.ncols()
3
sage: A.nrows()
2

AUTHORS:

Naqi Jaffery (2006-01-24): examples

nonpivots()¶

Return the list of i such that the i-th column of self is NOT a pivot column of the reduced row echelon form of self.

OUTPUT:

list - sorted list of (Python) integers

EXAMPLES:

sage: a = matrix(QQ,3,3,range(9)); a
[0 1 2]
[3 4 5]
[6 7 8]
sage: a.echelon_form()
[ 1  0 -1]
[ 0  1  2]
[ 0  0  0]
sage: a.nonpivots()
[2]

nonzero_positions(copy=True, column_order=False)¶

Returns the sorted list of pairs (i,j) such that self[i,j] != 0.

INPUT:

copy - (default: True) It is safe to change the resulting list (unless you give the option copy=False).
column_order - (default: False) If true, returns the list of pairs (i,j) such that self[i,j] != 0, but sorted by columns, i.e., column j=0 entries occur first, then column j=1 entries, etc.

EXAMPLES:

sage: a = matrix(QQ, 2,3, [1,2,0,2,0,0]); a
[1 2 0]
[2 0 0]
sage: a.nonzero_positions()
[(0, 0), (0, 1), (1, 0)]
sage: a.nonzero_positions(copy=False)
[(0, 0), (0, 1), (1, 0)]
sage: a.nonzero_positions(column_order=True)
[(0, 0), (1, 0), (0, 1)]
sage: a = matrix(QQ, 2,3, [1,2,0,2,0,0], sparse=True); a
[1 2 0]
[2 0 0]
sage: a.nonzero_positions()
[(0, 0), (0, 1), (1, 0)]
sage: a.nonzero_positions(copy=False)
[(0, 0), (0, 1), (1, 0)]
sage: a.nonzero_positions(column_order=True)
[(0, 0), (1, 0), (0, 1)]

nonzero_positions_in_column(i)¶

Return a sorted list of the integers j such that self[j,i] is nonzero, i.e., such that the j-th position of the i-th column is nonzero.

INPUT:

i - an integer

OUTPUT: list

EXAMPLES:

sage: a = matrix(QQ, 3,2, [1,2,0,2,0,0]); a
[1 2]
[0 2]
[0 0]
sage: a.nonzero_positions_in_column(0)
[0]
sage: a.nonzero_positions_in_column(1)
[0, 1]

You’ll get an IndexError, if you select an invalid column:

sage: a.nonzero_positions_in_column(2)
...
IndexError: matrix column index out of range

nonzero_positions_in_row(i)¶

Return the integers j such that self[i,j] is nonzero, i.e., such that the j-th position of the i-th row is nonzero.

INPUT:

i - an integer

OUTPUT: list

EXAMPLES:

sage: a = matrix(QQ, 3,2, [1,2,0,2,0,0]); a
[1 2]
[0 2]
[0 0]
sage: a.nonzero_positions_in_row(0)
[0, 1]
sage: a.nonzero_positions_in_row(1)
[1]
sage: a.nonzero_positions_in_row(2)
[]

nrows()¶

Return the number of rows of this matrix.

EXAMPLES:

sage: M = MatrixSpace(QQ,6,7)
sage: A = M([1,2,3,4,5,6,7, 22,3/4,34,11,7,5,3, 99,65,1/2,2/3,3/5,4/5,5/6, 9,8/9, 9/8,7/6,6/7,76,4, 0,9,8,7,6,5,4, 123,99,91,28,6,1024,1])
sage: A
[   1    2    3    4    5    6    7]
[  22  3/4   34   11    7    5    3]
[  99   65  1/2  2/3  3/5  4/5  5/6]
[   9  8/9  9/8  7/6  6/7   76    4]
[   0    9    8    7    6    5    4]
[ 123   99   91   28    6 1024    1]
sage: A.ncols()
7
sage: A.nrows()
6

AUTHORS:

Naqi Jaffery (2006-01-24): examples

pivots()¶

Return the pivot column positions of this matrix as a list of Python integers.

This returns a list, of the position of the first nonzero entry in each row of the echelon form.

OUTPUT:

list - a list of Python ints

EXAMPLES:

rank()¶

rescale_col(i, s, start_row=0)¶

Replace i-th col of self by s times i-th col of self.

INPUT:

i - ith column
s - scalar
start_row - only rescale entries at this row and lower

EXAMPLES: We rescale the last column of a matrix over the rational numbers:

sage: a = matrix(QQ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.rescale_col(2,1/2); a
[  0   1   1]
[  3   4 5/2]
sage: R.<x> = QQ[]

We rescale the last column of a matrix over a polynomial ring:

sage: a = matrix(R,2,3,[1,x,x^2,x^3,x^4,x^5]); a
[  1   x x^2]
[x^3 x^4 x^5]
sage: a.rescale_col(2,1/2); a
[      1       x 1/2*x^2]
[    x^3     x^4 1/2*x^5]

We try and fail to rescale a matrix over the integers by a non-integer:

sage: a = matrix(ZZ,2,3,[0,1,2, 3,4,4]); a
[0 1 2]
[3 4 4]
sage: a.rescale_col(2,1/2)
...
TypeError: Rescaling column by Rational Field element cannot be done over Integer Ring, use change_ring or with_rescaled_col instead.

To rescale the matrix by 1/2, you must change the base ring to the rationals:

sage: a = a.change_ring(QQ); a
[0 1 2]
[3 4 4]
sage: a.rescale_col(2,1/2); a
[0 1 1]
[3 4 2]

rescale_row(i, s, start_col=0)¶

Replace i-th row of self by s times i-th row of self.

INPUT:

i - ith row
s - scalar
start_col - only rescale entries at this column and to the right

EXAMPLES: We rescale the second row of a matrix over the rational numbers:

sage: a = matrix(QQ,3,range(6)); a
[0 1]
[2 3]
[4 5]
sage: a.rescale_row(1,1/2); a
[ 0   1]
[ 1 3/2]
[ 4   5]

We rescale the second row of a matrix over a polynomial ring:

sage: R.<x> = QQ[]
sage: a = matrix(R,3,[1,x,x^2,x^3,x^4,x^5]);a
[  1   x]
[x^2 x^3]
[x^4 x^5]
sage: a.rescale_row(1,1/2); a
[      1       x]
[1/2*x^2 1/2*x^3]
[    x^4     x^5]

We try and fail to rescale a matrix over the integers by a non-integer:

sage: a = matrix(ZZ,2,3,[0,1,2, 3,4,4]); a
[0 1 2]
[3 4 4]
sage: a.rescale_row(1,1/2)
...
TypeError: Rescaling row by Rational Field element cannot be done over Integer Ring, use change_ring or with_rescaled_row instead.

To rescale the matrix by 1/2, you must change the base ring to the rationals:

sage: a = a.change_ring(QQ); a
[0 1 2]
[3 4 4]
sage: a.rescale_col(1,1/2); a
[  0 1/2   2]
[  3   2   4]

set_col_to_multiple_of_col(i, j, s)¶

Set column i equal to s times column j.

EXAMPLES: We change the second column to -3 times the first column.

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.set_col_to_multiple_of_col(1,0,-3)
sage: a
[ 0  0  2]
[ 3 -9  5]

If we try to multiply a column by a rational number, we get an error message:

sage: a.set_col_to_multiple_of_col(1,0,1/2)
...
TypeError: Multiplying column by Rational Field element cannot be done over Integer Ring, use change_ring or with_col_set_to_multiple_of_col instead.

set_immutable()¶

Call this function to matrix a matrix immutable.

Matrices are always mutable by default, i.e., you can change their entries using A[i,j] = x. However, mutable matrices aren’t hashable, so can’t be used as keys in dictionaries, etc. Also, often when implementing a class, you might compute a matrix associated to it, e.g., the matrix of a Hecke operator. If you return this matrix to the user you’re really returning a reference and the user could then change an entry; this could be confusing. Thus you should set such a matrix immutable.

EXAMPLES:

sage: A = Matrix(QQ, 2, 2, range(4))
sage: A.is_mutable()
True
sage: A[0,0] = 10
sage: A
[10   1]
[ 2   3]

Mutable matrices are not hashable, so can’t be used as keys for dictionaries:

sage: hash(A)
...
TypeError: mutable matrices are unhashable
sage: v = {A:1}
...
TypeError: mutable matrices are unhashable

If we make A immutable it suddenly is hashable.

sage: A.set_immutable()
sage: A.is_mutable()
False
sage: A[0,0] = 10
...
ValueError: matrix is immutable; please change a copy instead (i.e., use copy(M) to change a copy of M).
sage: hash(A)
12
sage: v = {A:1}; v
{[10  1]
 [ 2  3]: 1}

set_row_to_multiple_of_row(i, j, s)¶

Set row i equal to s times row j.

EXAMPLES: We change the second row to -3 times the first row:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.set_row_to_multiple_of_row(1,0,-3)
sage: a
[ 0  1  2]
[ 0 -3 -6]

If we try to multiply a row by a rational number, we get an error message:

sage: a.set_row_to_multiple_of_row(1,0,1/2)
...
TypeError: Multiplying row by Rational Field element cannot be done over Integer Ring, use change_ring or with_row_set_to_multiple_of_row instead.

str()¶

EXAMPLES:

sage: R = PolynomialRing(QQ,6,'z')
sage: a = matrix(2,3, R.gens())
sage: a.__repr__()
'[z0 z1 z2]\n[z3 z4 z5]'

subdivisions¶

swap_columns(c1, c2)¶

Swap columns c1 and c2 of self.

EXAMPLES: We create a rational matrix:

sage: M = MatrixSpace(QQ,3,3)
sage: A = M([1,9,-7,4/5,4,3,6,4,3])
sage: A
[  1   9  -7]
[4/5   4   3]
[  6   4   3]

Since the first column is numbered zero, this swaps the second and third columns:

sage: A.swap_columns(1,2); A
[  1  -7   9]
[4/5   3   4]
[  6   3   4]

swap_rows(r1, r2)¶

Swap rows r1 and r2 of self.

EXAMPLES: We create a rational matrix:

sage: M = MatrixSpace(QQ,3,3)
sage: A = M([1,9,-7,4/5,4,3,6,4,3])
sage: A
[  1   9  -7]
[4/5   4   3]
[  6   4   3]

Since the first row is numbered zero, this swaps the first and third rows:

sage: A.swap_rows(0,2); A
[  6   4   3]
[4/5   4   3]
[  1   9  -7]

with_added_multiple_of_column(i, j, s, start_row=0)¶

Add s times column j to column i, returning new matrix.

EXAMPLES: We add -1 times the third column to the second column of an integer matrix, remembering to start numbering cols at zero:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: b = a.with_added_multiple_of_column(1,2,-1); b
[ 0 -1  2]
[ 3 -1  5]           

The original matrix is unchanged:

sage: a
[0 1 2]
[3 4 5]        

Adding a rational multiple is okay, and reassigning a variable is okay:

sage: a = a.with_added_multiple_of_column(0,1,1/3); a
[ 1/3    1    2]
[13/3    4    5]

with_added_multiple_of_row(i, j, s, start_col=0)¶

Add s times row j to row i, returning new matrix.

EXAMPLES: We add -3 times the first row to the second row of an integer matrix, remembering to start numbering rows at zero:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]        
sage: b = a.with_added_multiple_of_row(1,0,-3); b
[ 0  1  2]
[ 3  1 -1]

The original matrix is unchanged:

sage: a
[0 1 2]
[3 4 5]        

Adding a rational multiple is okay, and reassigning a variable is okay:

sage: a = a.with_added_multiple_of_row(0,1,1/3); a
[   1  7/3 11/3]
[   3    4    5]

with_col_set_to_multiple_of_col(i, j, s)¶

Set column i equal to s times column j, returning a new matrix.

EXAMPLES: We change the second column to -3 times the first column.

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: b = a.with_col_set_to_multiple_of_col(1,0,-3); b
[ 0  0  2]
[ 3 -9  5]

Note that the original matrix is unchanged:

sage: a
[0 1 2]
[3 4 5]

Adding a rational multiple is okay, and reassigning a variable is okay:

sage: a = a.with_col_set_to_multiple_of_col(1,0,1/2); a
[  0   0   2]
[  3 3/2   5]

with_rescaled_col(i, s, start_row=0)¶

Replaces i-th col of self by s times i-th col of self, returning new matrix.

EXAMPLES: We rescale the last column of a matrix over the integers:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: b = a.with_rescaled_col(2,-2); b
[  0   1  -4]
[  3   4 -10]           

The original matrix is unchanged:

sage: a
[0 1 2]
[3 4 5]        

Adding a rational multiple is okay, and reassigning a variable is okay:

sage: a = a.with_rescaled_col(1,1/3); a 
[  0 1/3   2]
[  3 4/3   5]

with_rescaled_row(i, s, start_col=0)¶

Replaces i-th row of self by s times i-th row of self, returning new matrix.

EXAMPLES: We rescale the second row of a matrix over the integers:

sage: a = matrix(ZZ,3,2,range(6)); a
[0 1]
[2 3]
[4 5]
sage: b = a.with_rescaled_row(1,-2); b
[ 0  1]
[-4 -6]
[ 4  5]

The original matrix is unchanged:

sage: a
[0 1]
[2 3]
[4 5]

Adding a rational multiple is okay, and reassigning a variable is okay:

sage: a = a.with_rescaled_row(2,1/3); a 
[  0   1]
[  2   3]
[4/3 5/3]

with_row_set_to_multiple_of_row(i, j, s)¶

Set row i equal to s times row j, returning a new matrix.

EXAMPLES: We change the second row to -3 times the first row:

sage: a = matrix(ZZ,2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: b = a.with_row_set_to_multiple_of_row(1,0,-3); b
[ 0  1  2]
[ 0 -3 -6]

Note that the original matrix is unchanged:

sage: a
[0 1 2]
[3 4 5]

Adding a rational multiple is okay, and reassigning a variable is okay:

sage: a = a.with_row_set_to_multiple_of_row(1,0,1/2); a
[  0   1   2]
[  0 1/2   1]

sage.matrix.matrix0.set_max_cols(n)¶

sage.matrix.matrix0.set_max_rows(n)¶

sage.matrix.matrix0.unpickle(cls, parent, mutability, cache, data, version)¶

Unpickle a matrix. This is only used internally by Sage. Users should never call this function directly.

EXAMPLES: We illustrating saving and loading several different types of matrices.

OVER $\ZZ$ :

sage: A = matrix(ZZ,2,range(4))
sage: loads(dumps(A))
[0 1]
[2 3]

Sparse OVER $\QQ$ :

Dense over $\QQ[x,y]$ :

Dense over finite field.

Base class for matrices, part 0¶

Previous topic

Next topic

This Page

Navigation

Base class for matrices, part 0¶

Previous topic

Next topic

This Page

Quick search

Navigation