Base class for matrices, part 1

For design documentation see sage.matrix.docs.

TESTS:

sage: A = Matrix(GF(5),3,3,srange(9))
sage: TestSuite(A).run()

class sage.matrix.matrix1.Matrix

Bases: sage.matrix.matrix0.Matrix

augment(other)

Return the augmented matrix of the form:

[self | other].

EXAMPLES:

sage: M = MatrixSpace(QQ,2,2)
sage: A = M([1,2, 3,4])
sage: A
[1 2]
[3 4]
sage: N = MatrixSpace(QQ,2,1)
sage: B = N([9,8])
sage: B
[9]
[8]
sage: A.augment(B)
[1 2 9]
[3 4 8]
sage: B.augment(A)
[9 1 2]
[8 3 4]
sage: M = MatrixSpace(QQ,3,4)
sage: A = M([1,2,3,4, 0,9,8,7, 2/3,3/4,4/5,9/8])
sage: A
[  1   2   3   4]
[  0   9   8   7]
[2/3 3/4 4/5 9/8]
sage: N = MatrixSpace(QQ,3,2)
sage: B = N([1,2, 3,4, 4,5])
sage: B
[1 2]
[3 4]
[4 5]
sage: A.augment(B)
[  1   2   3   4   1   2]
[  0   9   8   7   3   4]
[2/3 3/4 4/5 9/8   4   5]
sage: B.augment(A)
[  1   2   1   2   3   4]
[  3   4   0   9   8   7]
[  4   5 2/3 3/4 4/5 9/8]

AUTHORS:

• Naqi Jaffery (2006-01-24): examples

block_sum(other)

Return the block matrix that has self and other on the diagonal:

[ self     0 ]
[    0 other ]

EXAMPLES:

sage: A = matrix(QQ[['t']], 2, range(1, 5))
sage: A.block_sum(100*A)
[  1   2   0   0]
[  3   4   0   0]
[  0   0 100 200]
[  0   0 300 400]

column(i, from_list=False)

Return the i‘th column of this matrix as a vector.

This column is a dense vector if and only if the matrix is a dense matrix.

INPUT:

• i - integer
• from_list - bool (default: False); if true, returns the i‘th element of self.columns() (see columns()), which may be faster, but requires building a list of all columns the first time it is called after an entry of the matrix is changed.

EXAMPLES:

sage: a = matrix(2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.column(1)
(1, 4)

If the column is negative, it wraps around, just like with list indexing, e.g., -1 gives the right-most column:

sage: a.column(-1)
(2, 5)

TESTS:

sage: a = matrix(2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.column(3)
...
IndexError: column index out of range
sage: a.column(-4)
...
IndexError: column index out of range

columns(copy=True)

Return a list of the columns of self.

INPUT:

• copy - (default: True) if True, return a copy of the list

  of columns which is safe to change.

If self is sparse, returns columns as sparse vectors, and if self is dense returns them as dense vectors.

EXAMPLES:

sage: matrix(3, [1..9]).columns()
[(1, 4, 7), (2, 5, 8), (3, 6, 9)]
sage: matrix(RR, 2, [sqrt(2), pi, exp(1), 0]).columns()
[(1.41421356237310, 2.71828182845905), (3.14159265358979, 0.000000000000000)]
sage: matrix(RR, 0, 2, []).columns()
[(), ()]
sage: matrix(RR, 2, 0, []).columns()
[]
sage: m = matrix(RR, 3, 3, {(1,2): pi, (2, 2): -1, (0,1): sqrt(2)})
sage: parent(m.columns()[0])
Sparse vector space of dimension 3 over Real Field with 53 bits of precision

dense_columns(copy=True)

Return list of the dense columns of self.

INPUT:

• copy - (default: True) if True, return a copy so you can modify it safely

EXAMPLES:

An example over the integers:

sage: a = matrix(3,3,range(9)); a
[0 1 2]
[3 4 5]
[6 7 8]
sage: a.dense_columns()
[(0, 3, 6), (1, 4, 7), (2, 5, 8)]        

We do an example over a polynomial ring:

sage: R.<x> = QQ[ ]
sage: a = matrix(R, 2, [x,x^2, 2/3*x,1+x^5]); a
[      x     x^2]
[  2/3*x x^5 + 1]
sage: a.dense_columns()
[(x, 2/3*x), (x^2, x^5 + 1)]
sage: a = matrix(R, 2, [x,x^2, 2/3*x,1+x^5], sparse=True)
sage: c = a.dense_columns(); c
[(x, 2/3*x), (x^2, x^5 + 1)]
sage: parent(c[1])
Ambient free module of rank 2 over the principal ideal domain Univariate Polynomial Ring in x over Rational Field

dense_matrix()

If this matrix is sparse, return a dense matrix with the same entries. If this matrix is dense, return this matrix (not a copy).

Note

The definition of “dense” and “sparse” in Sage have nothing to do with the number of nonzero entries. Sparse and dense are properties of the underlying representation of the matrix.

EXAMPLES:

sage: A = MatrixSpace(QQ,2, sparse=True)([1,2,0,1])
sage: A.is_sparse()
True
sage: B = A.dense_matrix()
sage: B.is_sparse()
False
sage: A*B
[1 4]
[0 1]
sage: A.parent()
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: B.parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field

In Sage, the product of a sparse and a dense matrix is always dense:

sage: (A*B).parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: (B*A).parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field

TESTS:

Make sure that subdivisions are preserved when switching between dense and sparse matrices:

sage: a = matrix(ZZ, 3, range(9))
sage: a.subdivide([1,2],2)
sage: a.get_subdivisions()
([1, 2], [2])
sage: b = a.sparse_matrix().dense_matrix()
sage: b.get_subdivisions()
([1, 2], [2])

dense_rows(copy=True)

Return list of the dense rows of self.

INPUT:

• copy - (default: True) if True, return a copy so you can modify it safely (note that the individual vectors in the copy should not be modified since they are mutable!)

EXAMPLES:

sage: m = matrix(3, range(9)); m
[0 1 2]
[3 4 5]
[6 7 8]
sage: v = m.dense_rows(); v
[(0, 1, 2), (3, 4, 5), (6, 7, 8)]
sage: v is m.dense_rows()
False
sage: m.dense_rows(copy=False) is m.dense_rows(copy=False)
True
sage: m[0,0] = 10
sage: m.dense_rows()
[(10, 1, 2), (3, 4, 5), (6, 7, 8)]

lift()

Return lift of self to the covering ring of the base ring R, which is by definition the ring returned by calling cover_ring() on R, or just R itself if the cover_ring method is not defined.

EXAMPLES:

sage: M = Matrix(Integers(7), 2, 2, [5, 9, 13, 15]) ; M
[5 2]
[6 1]
sage: M.lift()
[5 2]
[6 1]
sage: parent(M.lift())
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring

The field QQ doesn’t have a cover_ring method:

sage: hasattr(QQ, 'cover_ring')
False

So lifting a matrix over QQ gives back the same exact matrix.

sage: B = matrix(QQ, 2, [1..4])
sage: B.lift()
[1 2]
[3 4]
sage: B.lift() is B
True

matrix_from_columns(columns)

Return the matrix constructed from self using columns with indices in the columns list.

EXAMPLES:

sage: M = MatrixSpace(Integers(8),3,3)
sage: A = M(range(9)); A
[0 1 2]
[3 4 5]
[6 7 0]
sage: A.matrix_from_columns([2,1])
[2 1]
[5 4]
[0 7]

matrix_from_rows(rows)

Return the matrix constructed from self using rows with indices in the rows list.

EXAMPLES:

sage: M = MatrixSpace(Integers(8),3,3)
sage: A = M(range(9)); A
[0 1 2]
[3 4 5]
[6 7 0]
sage: A.matrix_from_rows([2,1])
[6 7 0]
[3 4 5]

matrix_from_rows_and_columns(rows, columns)

Return the matrix constructed from self from the given rows and columns.

EXAMPLES:

sage: M = MatrixSpace(Integers(8),3,3)
sage: A = M(range(9)); A
[0 1 2]
[3 4 5]
[6 7 0]
sage: A.matrix_from_rows_and_columns([1], [0,2])
[3 5]
sage: A.matrix_from_rows_and_columns([1,2], [1,2])
[4 5]
[7 0]

Note that row and column indices can be reordered or repeated:

sage: A.matrix_from_rows_and_columns([2,1], [2,1])
[0 7]
[5 4]

For example here we take from row 1 columns 2 then 0 twice, and do this 3 times.

sage: A.matrix_from_rows_and_columns([1,1,1],[2,0,0])
[5 3 3]
[5 3 3]
[5 3 3]

AUTHORS:

• Jaap Spies (2006-02-18)
• Didier Deshommes: some Pyrex speedups implemented

matrix_over_field()

Return copy of this matrix, but with entries viewed as elements of the fraction field of the base ring (assuming it is defined).

EXAMPLES:

sage: A = MatrixSpace(IntegerRing(),2)([1,2,3,4])
sage: B = A.matrix_over_field()
sage: B
[1 2]
[3 4]
sage: B.parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field

matrix_space(nrows=None, ncols=None, sparse=None)

Return the ambient matrix space of self.

INPUT:

• nrows, ncols - (optional) number of rows and columns in returned matrix space.
• sparse - whether the returned matrix space uses sparse or dense matrices.

EXAMPLES:

sage: m = matrix(3, [1..9])
sage: m.matrix_space()
Full MatrixSpace of 3 by 3 dense matrices over Integer Ring
sage: m.matrix_space(ncols=2)
Full MatrixSpace of 3 by 2 dense matrices over Integer Ring
sage: m.matrix_space(1)      
Full MatrixSpace of 1 by 3 dense matrices over Integer Ring
sage: m.matrix_space(1, 2, True) 
Full MatrixSpace of 1 by 2 sparse matrices over Integer Ring

new_matrix(nrows=None, ncols=None, entries=0, coerce=True, copy=True, sparse=None)

Create a matrix in the parent of this matrix with the given number of rows, columns, etc. The default parameters are the same as for self.

INPUT:

These three variables get sent to matrix_space():

• nrows, ncols - number of rows and columns in returned matrix. If not specified, defaults to None and will give a matrix of the same size as self.
• sparse - whether returned matrix is sparse or not. Defaults to same value as self.

The remaining three variables (coerce, entries, and copy) are used by sage.matrix.matrix_space.MatrixSpace() to construct the new matrix.

Warning

This function called with no arguments returns the zero matrix of the same dimension and sparseness of self.

EXAMPLES:

sage: A = matrix(ZZ,2,2,[1,2,3,4]); A [1 2] [3 4] sage: A.new_matrix() [0 0] [0 0] sage: A.new_matrix(1,1) [0] sage: A.new_matrix(3,3).parent() Full MatrixSpace of 3 by 3 dense matrices over Integer Ring

sage: A = matrix(RR,2,3,[1.1,2.2,3.3,4.4,5.5,6.6]); A
[1.10000000000000 2.20000000000000 3.30000000000000]
[4.40000000000000 5.50000000000000 6.60000000000000]
sage: A.new_matrix()
[0.000000000000000 0.000000000000000 0.000000000000000]
[0.000000000000000 0.000000000000000 0.000000000000000]
sage: A.new_matrix().parent()
Full MatrixSpace of 2 by 3 dense matrices over Real Field with 53 bits of precision

numpy(dtype=None)

Return the Numpy matrix associated to this matrix.

INPUT:

• dtype - The desired data-type for the array. If not given, then the type will be determined as the minimum type required to hold the objects in the sequence.

EXAMPLES:

sage: a = matrix(3,range(12))
sage: a.numpy()
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
sage: a.numpy('f')
array([[  0.,   1.,   2.,   3.],
       [  4.,   5.,   6.,   7.],
       [  8.,   9.,  10.,  11.]], dtype=float32)
sage: a.numpy('d')
array([[  0.,   1.,   2.,   3.],
       [  4.,   5.,   6.,   7.],
       [  8.,   9.,  10.,  11.]])
sage: a.numpy('B')
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]], dtype=uint8)

Type numpy.typecodes for a list of the possible typecodes:

sage: import numpy
sage: sorted(numpy.typecodes.items())
[('All', '?bhilqpBHILQPfdgFDGSUVO'), ('AllFloat', 'fdgFDG'), ('AllInteger', 'bBhHiIlLqQpP'), ('Character', 'c'), ('Complex', 'FDG'), ('Float', 'fdg'), ('Integer', 'bhilqp'), ('UnsignedInteger', 'BHILQP')]

Alternatively, numpy automatically calls this function (via the magic __array__() method) to convert Sage matrices to numpy arrays:

sage: import numpy
sage: b=numpy.array(a); b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
sage: b.dtype
dtype('int32')  # 32-bit
dtype('int64')  # 64-bit
sage: b.shape
(3, 4)

row(i, from_list=False)

Return the i‘th row of this matrix as a vector.

This row is a dense vector if and only if the matrix is a dense matrix.

INPUT:

• i - integer
• from_list - bool (default: False); if true, returns the i‘th element of self.rows() (see rows()), which may be faster, but requires building a list of all rows the first time it is called after an entry of the matrix is changed.

EXAMPLES:

sage: a = matrix(2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.row(0)
(0, 1, 2)
sage: a.row(1)
(3, 4, 5)
sage: a.row(-1)  # last row
(3, 4, 5)

TESTS:

sage: a = matrix(2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: a.row(2)
...
IndexError: row index out of range
sage: a.row(-3)
...
IndexError: row index out of range

rows(copy=True)

Return a list of the rows of self.

INPUT:

• copy - (default: True) if True, return a copy of the list of rows which is safe to change.

If self is sparse, returns rows as sparse vectors, and if self is dense returns them as dense vectors.

EXAMPLES:

sage: matrix(3, [1..9]).rows()
[(1, 2, 3), (4, 5, 6), (7, 8, 9)]
sage: matrix(RR, 2, [sqrt(2), pi, exp(1), 0]).rows()
[(1.41421356237310, 3.14159265358979), (2.71828182845905, 0.000000000000000)]
sage: matrix(RR, 0, 2, []).rows()
[]
sage: matrix(RR, 2, 0, []).rows()
[(), ()]
sage: m = matrix(RR, 3, 3, {(1,2): pi, (2, 2): -1, (0,1): sqrt(2)})
sage: parent(m.rows()[0])
Sparse vector space of dimension 3 over Real Field with 53 bits of precision

set_column(col, v)

Sets the entries of column col in self to be the entries of v.

EXAMPLES:

sage: A = matrix([[1,2],[3,4]]); A
[1 2]
[3 4]
sage: A.set_column(0, [0,0]); A
[0 2]
[0 4]
sage: A.set_column(1, [0,0]); A
[0 0]
[0 0]
sage: A.set_column(2, [0,0]); A
...
IndexError: index out of range

sage: A.set_column(0, [0,0,0])
...
ValueError: v must be of length 2

set_row(row, v)

Sets the entries of row row in self to be the entries of v.

EXAMPLES:

sage: A = matrix([[1,2],[3,4]]); A
[1 2]
[3 4]
sage: A.set_row(0, [0,0]); A
[0 0]
[3 4]
sage: A.set_row(1, [0,0]); A
[0 0]
[0 0]
sage: A.set_row(2, [0,0]); A
...
IndexError: index out of range

sage: A.set_row(0, [0,0,0])
...
ValueError: v must be of length 2

sparse_columns(copy=True)

Return list of the sparse columns of self.

INPUT:

• copy - (default: True) if True, return a copy so you can

  modify it safely

EXAMPLES:

sage: a = matrix(2,3,range(6)); a
[0 1 2]
[3 4 5]
sage: v = a.sparse_columns(); v
[(0, 3), (1, 4), (2, 5)]
sage: v[1].is_sparse()
True

sparse_matrix()

If this matrix is dense, return a sparse matrix with the same entries. If this matrix is sparse, return this matrix (not a copy).

Note

The definition of “dense” and “sparse” in Sage have nothing to do with the number of nonzero entries. Sparse and dense are properties of the underlying representation of the matrix.

EXAMPLES:

sage: A = MatrixSpace(QQ,2, sparse=False)([1,2,0,1])
sage: A.is_sparse()
False
sage: B = A.sparse_matrix()
sage: B.is_sparse()
True
sage: A
[1 2]
[0 1]
sage: B
[1 2]
[0 1]
sage: A*B
[1 4]
[0 1]
sage: A.parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: B.parent()
Full MatrixSpace of 2 by 2 sparse matrices over Rational Field
sage: (A*B).parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: (B*A).parent()
Full MatrixSpace of 2 by 2 dense matrices over Rational Field

sparse_rows(copy=True)

Return list of the sparse rows of self.

INPUT:

• copy - (default: True) if True, return a copy so you can

  modify it safely

EXAMPLES:

sage: m = Mat(ZZ,3,3,sparse=True)(range(9)); m
[0 1 2]
[3 4 5]
[6 7 8]
sage: v = m.sparse_rows(); v
[(0, 1, 2), (3, 4, 5), (6, 7, 8)]
sage: m.sparse_rows(copy=False) is m.sparse_rows(copy=False)
True
sage: v[1].is_sparse()
True
sage: m[0,0] = 10
sage: m.sparse_rows()
[(10, 1, 2), (3, 4, 5), (6, 7, 8)]

stack(other)

Return the augmented matrix self on top of other:

[ self  ]
[ other ]

EXAMPLES:

sage: M = Matrix(QQ, 2, 3, range(6))
sage: N = Matrix(QQ, 1, 3, [10,11,12])
sage: M.stack(N)
[ 0  1  2]
[ 3  4  5]
[10 11 12]

submatrix(row=0, col=0, nrows=-1, ncols=-1)

Return the matrix constructed from self using the specified range of rows and columns.

INPUT:

• row, col - index of the starting row and column. Indices start at zero.
• nrows, ncols - (optional) number of rows and columns to take. If not provided, take all rows below and all columns to the right of the starting entry.

SEE ALSO:

The functions matrix_from_rows(), matrix_from_columns(), and matrix_from_rows_and_columns() allow one to select arbitrary subsets of rows and/or columns.

EXAMPLES:

Take the 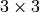submatrix starting from entry (1,1) in a 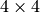matrix:

sage: m = matrix(4, [1..16])
sage: m.submatrix(1, 1)
[ 6  7  8]
[10 11 12]
[14 15 16]

Same thing, except take only two rows:

sage: m.submatrix(1, 1, 2)
[ 6  7  8]
[10 11 12]

And now take only one column:

sage: m.submatrix(1, 1, 2, 1)
[ 6]
[10]

You can take zero rows or columns if you want:

sage: m.submatrix(1, 1, 0)
[]
sage: parent(m.submatrix(1, 1, 0))
Full MatrixSpace of 0 by 3 dense matrices over Integer Ring