Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Graph Theory »

This module implements many graph theoretic operations and concepts.
AUTHORS:
Robert L. Miller (2006-10-22): initial version
William Stein (2006-12-05): Editing
Robert L. Miller (2007-01-13): refactoring, adjusting for NetworkX-0.33, fixed plotting bugs (2007-01-23): basic tutorial, edge labels, loops, multiple edges and arcs (2007-02-07): graph6 and sparse6 formats, matrix input
Emily Kirkmann (2007-02-11): added graph_border option to plot and show
Robert L. Miller (2007-02-12): vertex color-maps, graph boundaries, graph6 helper functions in Cython
Robert L. Miller Sage Days 3 (2007-02-17-21): 3d plotting in Tachyon
Robert L. Miller (2007-02-25): display a partition
Robert L. Miller (2007-02-28): associate arbitrary objects to vertices, edge and arc label display (in 2d), edge coloring
Robert L. Miller (2007-03-21): Automorphism group, isomorphism check, canonical label
Robert L. Miller (2007-06-07-09): NetworkX function wrapping
Michael W. Hansen (2007-06-09): Topological sort generation
Emily Kirkman, Robert L. Miller Sage Days 4: Finished wrapping NetworkX
Emily Kirkman (2007-07-21): Genus (including circular planar, all embeddings and all planar embeddings), all paths, interior paths
Bobby Moretti (2007-08-12): fixed up plotting of graphs with edge colors differentiated by label
Jason Grout (2007-09-25): Added functions, bug fixes, and general enhancements
Robert L. Miller (Sage Days 7): Edge labeled graph isomorphism
Tom Boothby (Sage Days 7): Miscellaneous awesomeness
Tom Boothby (2008-01-09): Added graphviz output
David Joyner (2009-2): Fixed docstring bug related to GAP.
Stephen Hartke (2009-07-26): Fixed bug in blocks_and_cut_vertices() that caused an incorrect result when the vertex 0 was a cut vertex.
Stephen Hartke (2009-08-22): Fixed bug in blocks_and_cut_vertices() where the list of cut_vertices is not treated as a set.
Anders Jonsson (2009-10-10): Counting of spanning trees and out-trees added.
and everything that uses Linear Programming and class numerical.MIP
Nicolas M. Thiery (2010-02): graph layout code refactoring, dot2tex/graphviz interface
Sage graphs are actually NetworkX graphs, wrapped in a Sage class. In fact, any graph can produce its underlying NetworkX graph. For example,
sage: import networkx
sage: G = graphs.PetersenGraph()
sage: N = G.networkx_graph()
sage: isinstance(N, networkx.graph.Graph)
True
The NetworkX graph is essentially a dictionary of dictionaries of dictionaries:
sage: N.adj
{0: {1: {}, 4: {}, 5: {}}, 1: {0: {}, 2: {}, 6: {}}, 2: {1: {}, 3: {}, 7: {}}, 3: {8: {}, 2: {}, 4: {}}, 4: {0: {}, 9: {}, 3: {}}, 5: {0: {}, 8: {}, 7: {}}, 6: {8: {}, 1: {}, 9: {}}, 7: {9: {}, 2: {}, 5: {}}, 8: {3: {}, 5: {}, 6: {}}, 9: {4: {}, 6: {}, 7: {}}}
Each dictionary key is a vertex label, and each key in the following dictionary is a neighbor of that vertex. In undirected graphs, there is redundancy: for example, the dictionary containing the entry 1: {2: {}} implies it must contain {2: {1: {}}. The innermost entry of {} is related to edge labeling (see section Labels).
Sage Graphs can be created from a wide range of inputs. A few examples are covered here.
NetworkX dictionary format:
sage: d = {0: [1,4,5], 1: [2,6], 2: [3,7], 3: [4,8], 4: [9], \
5: [7, 8], 6: [8,9], 7: [9]}
sage: G = Graph(d); G
Graph on 10 vertices
sage: G.plot().show() # or G.show()
A NetworkX graph:
sage: K = networkx.complete_bipartite_graph(12,7)
sage: G = Graph(K)
sage: G.degree()
[7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 12, 12, 12, 12, 12, 12, 12]
graph6 or sparse6 format:
sage: s = ':I`AKGsaOs`cI]Gb~'
sage: G = Graph(s, sparse=True); G
Looped multi-graph on 10 vertices
sage: G.plot().show() # or G.show()
Note that the \ character is an escape character in Python, and also a character used by graph6 strings:
sage: G = Graph('Ihe\n@GUA')
...
RuntimeError: The string (Ihe) seems corrupt: for n = 10, the string is too short.
In Python, the escaped character \ is represented by \\:
sage: G = Graph('Ihe\\n@GUA')
sage: G.plot().show() # or G.show()
adjacency matrix: In an adjacency matrix, each column and each
row represent a vertex. If a 1 shows up in row  , column
, column
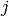 , there is an edge
, there is an edge 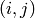 .
.
sage: M = Matrix([(0,1,0,0,1,1,0,0,0,0),(1,0,1,0,0,0,1,0,0,0), \
(0,1,0,1,0,0,0,1,0,0), (0,0,1,0,1,0,0,0,1,0),(1,0,0,1,0,0,0,0,0,1), \
(1,0,0,0,0,0,0,1,1,0), (0,1,0,0,0,0,0,0,1,1),(0,0,1,0,0,1,0,0,0,1), \
(0,0,0,1,0,1,1,0,0,0), (0,0,0,0,1,0,1,1,0,0)])
sage: M
[0 1 0 0 1 1 0 0 0 0]
[1 0 1 0 0 0 1 0 0 0]
[0 1 0 1 0 0 0 1 0 0]
[0 0 1 0 1 0 0 0 1 0]
[1 0 0 1 0 0 0 0 0 1]
[1 0 0 0 0 0 0 1 1 0]
[0 1 0 0 0 0 0 0 1 1]
[0 0 1 0 0 1 0 0 0 1]
[0 0 0 1 0 1 1 0 0 0]
[0 0 0 0 1 0 1 1 0 0]
sage: G = Graph(M); G
Graph on 10 vertices
sage: G.plot().show() # or G.show()
incidence matrix: In an incidence matrix, each row represents a vertex and each column represents an edge.
sage: M = Matrix([(-1,0,0,0,1,0,0,0,0,0,-1,0,0,0,0), \
(1,-1,0,0,0,0,0,0,0,0,0,-1,0,0,0),(0,1,-1,0,0,0,0,0,0,0,0,0,-1,0,0), \
(0,0,1,-1,0,0,0,0,0,0,0,0,0,-1,0),(0,0,0,1,-1,0,0,0,0,0,0,0,0,0,-1), \
(0,0,0,0,0,-1,0,0,0,1,1,0,0,0,0),(0,0,0,0,0,0,0,1,-1,0,0,1,0,0,0), \
(0,0,0,0,0,1,-1,0,0,0,0,0,1,0,0),(0,0,0,0,0,0,0,0,1,-1,0,0,0,1,0), \
(0,0,0,0,0,0,1,-1,0,0,0,0,0,0,1)])
sage: M
[-1 0 0 0 1 0 0 0 0 0 -1 0 0 0 0]
[ 1 -1 0 0 0 0 0 0 0 0 0 -1 0 0 0]
[ 0 1 -1 0 0 0 0 0 0 0 0 0 -1 0 0]
[ 0 0 1 -1 0 0 0 0 0 0 0 0 0 -1 0]
[ 0 0 0 1 -1 0 0 0 0 0 0 0 0 0 -1]
[ 0 0 0 0 0 -1 0 0 0 1 1 0 0 0 0]
[ 0 0 0 0 0 0 0 1 -1 0 0 1 0 0 0]
[ 0 0 0 0 0 1 -1 0 0 0 0 0 1 0 0]
[ 0 0 0 0 0 0 0 0 1 -1 0 0 0 1 0]
[ 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 1]
sage: G = Graph(M); G
Graph on 10 vertices
sage: G.plot().show() # or G.show()
sage: DiGraph(matrix(2,[0,0,-1,1]), format="incidence_matrix")
...
ValueError: There must be two nonzero entries (-1 & 1) per column.
If you wish to iterate through all the isomorphism types of graphs, type, for example:
sage: for g in graphs(4):
... print g.spectrum()
[0, 0, 0, 0]
[1, 0, 0, -1]
[1.4142135623..., 0, 0, -1.4142135623...]
[2, 0, -1, -1]
[1.7320508075..., 0, 0, -1.7320508075...]
[1, 1, -1, -1]
[1.6180339887..., 0.6180339887..., -0.6180339887..., -1.6180339887...]
[2.1700864866..., 0.3111078174..., -1, -1.4811943040...]
[2, 0, 0, -2]
[2.5615528128..., 0, -1, -1.5615528128...]
[3, -1, -1, -1]
For some commonly used graphs to play with, type
sage: graphs.[tab] # not tested
and hit {tab}. Most of these graphs come with their own custom plot, so you can see how people usually visualize these graphs.
sage: G = graphs.PetersenGraph()
sage: G.plot().show() # or G.show()
sage: G.degree_histogram()
[0, 0, 0, 10]
sage: G.adjacency_matrix()
[0 1 0 0 1 1 0 0 0 0]
[1 0 1 0 0 0 1 0 0 0]
[0 1 0 1 0 0 0 1 0 0]
[0 0 1 0 1 0 0 0 1 0]
[1 0 0 1 0 0 0 0 0 1]
[1 0 0 0 0 0 0 1 1 0]
[0 1 0 0 0 0 0 0 1 1]
[0 0 1 0 0 1 0 0 0 1]
[0 0 0 1 0 1 1 0 0 0]
[0 0 0 0 1 0 1 1 0 0]
sage: S = G.subgraph([0,1,2,3])
sage: S.plot().show() # or S.show()
sage: S.density()
1/2
sage: G = GraphQuery(display_cols=['graph6'], num_vertices=7, diameter=5)
sage: L = G.get_graphs_list()
sage: graphs_list.show_graphs(L)
Each vertex can have any hashable object as a label. These are
things like strings, numbers, and tuples. Each edge is given a
default label of None, but if specified, edges can
have any label at all. Edges between vertices 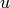 and
and
 are represented typically as (u, v, l), where
l is the label for the edge.
are represented typically as (u, v, l), where
l is the label for the edge.
Note that vertex labels themselves cannot be mutable items:
sage: M = Matrix( [[0,0],[0,0]] )
sage: G = Graph({ 0 : { M : None } })
...
TypeError: mutable matrices are unhashable
However, if one wants to define a dictionary, with the same keys and arbitrary objects for entries, one can make that association:
sage: d = {0 : graphs.DodecahedralGraph(), 1 : graphs.FlowerSnark(), \
2 : graphs.MoebiusKantorGraph(), 3 : graphs.PetersenGraph() }
sage: d[2]
Moebius-Kantor Graph: Graph on 16 vertices
sage: T = graphs.TetrahedralGraph()
sage: T.vertices()
[0, 1, 2, 3]
sage: T.set_vertices(d)
sage: T.get_vertex(1)
Flower Snark: Graph on 20 vertices
There is a database available for searching for graphs that satisfy a certain set of parameters, including number of vertices and edges, density, maximum and minimum degree, diameter, radius, and connectivity. To see a list of all search parameter keywords broken down by their designated table names, type
sage: graph_db_info()
{...}
For more details on data types or keyword input, enter
sage: GraphQuery? # not tested
The results of a query can be viewed with the show method, or can be viewed individually by iterating through the results:
sage: Q = GraphQuery(display_cols=['graph6'],num_vertices=7, diameter=5)
sage: Q.show()
Graph6
--------------------
F@?]O
F@OKg
F?`po
F?gqg
FIAHo
F@R@o
FA_pW
FGC{o
FEOhW
Show each graph as you iterate through the results:
sage: for g in Q:
... show(g)
To see a graph  you are working with, there
are three main options. You can view the graph in two dimensions via
matplotlib with show().
you are working with, there
are three main options. You can view the graph in two dimensions via
matplotlib with show().
sage: G = graphs.RandomGNP(15,.3)
sage: G.show()
And you can view it in three dimensions via jmol with show3d().
sage: G.show3d()
Or it can be rendered with 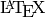 . This requires the right
additions to a standard
. This requires the right
additions to a standard 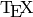 installation. Then standard
Sage commands, such as view(G) will display the graph, or
latex(G) will produce a string suitable for inclusion in a
installation. Then standard
Sage commands, such as view(G) will display the graph, or
latex(G) will produce a string suitable for inclusion in a
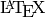 document. More details on this are at
the sage.graphs.graph_latex module.
document. More details on this are at
the sage.graphs.graph_latex module.
sage: from sage.graphs.graph_latex import check_tkz_graph
sage: check_tkz_graph() # random - depends on TeX installation
sage: latex(G)
\begin{tikzpicture}
...
\end{tikzpicture}
Bases: sage.graphs.generic_graph.GenericGraph
Undirected graph.
A graph is a set of vertices connected by edges. See also the Wikipedia article on graphs.
One can very easily create a graph in Sage by typing:
sage: g = Graph()
By typing the name of the graph, one can get some basic information about it:
sage: g
Graph on 0 vertices
This graph is not very interesting as it is by default the empty graph. But Sage contains a large collection of pre-defined graph classes that can be listed this way:
You will see a list of methods which will construct named graphs. For example:
sage: g = graphs.PetersenGraph()
sage: g.plot()
or:
sage: g = graphs.ChvatalGraph()
sage: g.plot()
In order to obtain more information about these graph constructors, access the documentation using the command graphs.RandomGNP?.
Once you have defined the graph you want, you can begin to work on it by using the almost 200 functions on graphs in the Sage library! If your graph is named g, you can list these functions as previously this way
As usual, you can get some information about what these functions do by typing (e.g. if you want to know about the diameter() method) g.diameter?.
If you have defined a graph g having several connected components (i.e. g.is_connected() returns False), you can print each one of its connected components with only two lines:
sage: for component in g.connected_components():
... g.subgraph(component).plot()
INPUT:
- A dictionary of dictionaries
- A dictionary of lists
- A NumPy matrix or ndarray
- A Sage adjacency matrix or incidence matrix
- A pygraphviz agraph
- A SciPy sparse matrix
- A NetworkX digraph
pos - a positioning dictionary: for example, the spring layout from NetworkX for the 5-cycle is:
{0: [-0.91679746, 0.88169588],
1: [ 0.47294849, 1.125 ],
2: [ 1.125 ,-0.12867615],
3: [ 0.12743933,-1.125 ],
4: [-1.125 ,-0.50118505]}
name - (must be an explicitly named parameter, i.e., name="complete") gives the graph a name
loops - boolean, whether to allow loops (ignored if data is an instance of the Graph class)
multiedges - boolean, whether to allow multiple edges (ignored if data is an instance of the Graph class)
weighted - whether graph thinks of itself as weighted or not. See self.weighted()
format - if None, Graph tries to guess- can be several values, including:
boundary - a list of boundary vertices, if empty, graph is considered as a ‘graph without boundary’
implementation - what to use as a backend for the graph. Currently, the options are either ‘networkx’ or ‘c_graph’
sparse - only for implementation == ‘c_graph’. Whether to use sparse or dense graphs as backend. Note that currently dense graphs do not have edge labels, nor can they be multigraphs
vertex_labels - only for implementation == ‘c_graph’. Whether to allow any object as a vertex (slower), or only the integers 0, ..., n-1, where n is the number of vertices.
EXAMPLES:
We illustrate the first six input formats (the other two involve packages that are currently not standard in Sage):
A dictionary of dictionaries:
sage: g = Graph({0:{1:'x',2:'z',3:'a'}, 2:{5:'out'}}); g
Graph on 5 vertices
The labels (‘x’, ‘z’, ‘a’, ‘out’) are labels for edges. For example, ‘out’ is the label for the edge on 2 and 5. Labels can be used as weights, if all the labels share some common parent.
sage: a,b,c,d,e,f = sorted(SymmetricGroup(3))
sage: Graph({b:{d:'c',e:'p'}, c:{d:'p',e:'c'}})
Graph on 4 vertices
A dictionary of lists:
sage: g = Graph({0:[1,2,3], 2:[4]}); g
Graph on 5 vertices
A list of vertices and a function describing adjacencies. Note that the list of vertices and the function must be enclosed in a list (i.e., [list of vertices, function]).
Construct the Paley graph over GF(13).
sage: g=Graph([GF(13), lambda i,j: i!=j and (i-j).is_square()])
sage: g.vertices()
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
sage: g.adjacency_matrix()
[0 1 0 1 1 0 0 0 0 1 1 0 1]
[1 0 1 0 1 1 0 0 0 0 1 1 0]
[0 1 0 1 0 1 1 0 0 0 0 1 1]
[1 0 1 0 1 0 1 1 0 0 0 0 1]
[1 1 0 1 0 1 0 1 1 0 0 0 0]
[0 1 1 0 1 0 1 0 1 1 0 0 0]
[0 0 1 1 0 1 0 1 0 1 1 0 0]
[0 0 0 1 1 0 1 0 1 0 1 1 0]
[0 0 0 0 1 1 0 1 0 1 0 1 1]
[1 0 0 0 0 1 1 0 1 0 1 0 1]
[1 1 0 0 0 0 1 1 0 1 0 1 0]
[0 1 1 0 0 0 0 1 1 0 1 0 1]
[1 0 1 1 0 0 0 0 1 1 0 1 0]
Construct the line graph of a complete graph.
sage: g=graphs.CompleteGraph(4)
sage: line_graph=Graph([g.edges(labels=false), \
lambda i,j: len(set(i).intersection(set(j)))>0], \
loops=False)
sage: line_graph.vertices()
[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]
sage: line_graph.adjacency_matrix()
[0 1 1 1 1 0]
[1 0 1 1 0 1]
[1 1 0 0 1 1]
[1 1 0 0 1 1]
[1 0 1 1 0 1]
[0 1 1 1 1 0]
A NumPy matrix or ndarray:
sage: import numpy
sage: A = numpy.array([[0,1,1],[1,0,1],[1,1,0]])
sage: Graph(A)
Graph on 3 vertices
A graph6 or sparse6 string: Sage automatically recognizes whether a string is in graph6 or sparse6 format:
sage: s = ':I`AKGsaOs`cI]Gb~'
sage: Graph(s,sparse=True)
Looped multi-graph on 10 vertices
sage: G = Graph('G?????')
sage: G = Graph("G'?G?C")
...
RuntimeError: The string seems corrupt: valid characters are
?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
sage: G = Graph('G??????')
...
RuntimeError: The string (G??????) seems corrupt: for n = 8, the string is too long.
sage: G = Graph(":I'AKGsaOs`cI]Gb~")
...
RuntimeError: The string seems corrupt: valid characters are
?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
There are also list functions to take care of lists of graphs:
sage: s = ':IgMoqoCUOqeb\n:I`AKGsaOs`cI]Gb~\n:I`EDOAEQ?PccSsge\N\n'
sage: graphs_list.from_sparse6(s)
[Looped multi-graph on 10 vertices, Looped multi-graph on 10 vertices, Looped multi-graph on 10 vertices]
A Sage matrix: Note: If format is not specified, then Sage assumes a symmetric square matrix is an adjacency matrix, otherwise an incidence matrix.
an adjacency matrix:
sage: M = graphs.PetersenGraph().am(); M
[0 1 0 0 1 1 0 0 0 0]
[1 0 1 0 0 0 1 0 0 0]
[0 1 0 1 0 0 0 1 0 0]
[0 0 1 0 1 0 0 0 1 0]
[1 0 0 1 0 0 0 0 0 1]
[1 0 0 0 0 0 0 1 1 0]
[0 1 0 0 0 0 0 0 1 1]
[0 0 1 0 0 1 0 0 0 1]
[0 0 0 1 0 1 1 0 0 0]
[0 0 0 0 1 0 1 1 0 0]
sage: Graph(M)
Graph on 10 vertices
sage: Graph(matrix([[1,2],[2,4]]),loops=True,sparse=True)
Looped multi-graph on 2 vertices
sage: M = Matrix([[0,1,-1],[1,0,-1/2],[-1,-1/2,0]]); M
[ 0 1 -1]
[ 1 0 -1/2]
[ -1 -1/2 0]
sage: G = Graph(M,sparse=True); G
Graph on 3 vertices
sage: G.weighted()
True
an incidence matrix:
sage: M = Matrix(6, [-1,0,0,0,1, 1,-1,0,0,0, 0,1,-1,0,0, 0,0,1,-1,0, 0,0,0,1,-1, 0,0,0,0,0]); M
[-1 0 0 0 1]
[ 1 -1 0 0 0]
[ 0 1 -1 0 0]
[ 0 0 1 -1 0]
[ 0 0 0 1 -1]
[ 0 0 0 0 0]
sage: Graph(M)
Graph on 6 vertices
sage: Graph(Matrix([[1],[1],[1]]))
...
ValueError: Non-symmetric or non-square matrix assumed to be an incidence matrix: There must be two nonzero entries (-1 & 1) per column.
sage: Graph(Matrix([[1],[1],[0]]))
...
ValueError: Non-symmetric or non-square matrix assumed to be an incidence matrix: Each column represents an edge: -1 goes to 1.
sage: M = Matrix([[0,1,-1],[1,0,-1],[-1,-1,0]]); M
[ 0 1 -1]
[ 1 0 -1]
[-1 -1 0]
sage: Graph(M,sparse=True)
Graph on 3 vertices
sage: M = Matrix([[0,1,1],[1,0,0],[0,0,0]]); M
[0 1 1]
[1 0 0]
[0 0 0]
sage: Graph(M)
...
ValueError: Non-symmetric or non-square matrix assumed to be an incidence matrix: There must be two nonzero entries (-1 & 1) per column.
sage: M = Matrix([[0,1,1],[1,0,1],[-1,-1,0]]); M
[ 0 1 1]
[ 1 0 1]
[-1 -1 0]
sage: Graph(M)
...
ValueError: Non-symmetric or non-square matrix assumed to be an incidence matrix: Each column represents an edge: -1 goes to 1.
A NetworkX MultiGraph:
sage: import networkx
sage: g = networkx.MultiGraph({0:[1,2,3], 2:[4]})
sage: Graph(g)
Graph on 5 vertices
A NetworkX graph:
sage: import networkx
sage: g = networkx.Graph({0:[1,2,3], 2:[4]})
sage: DiGraph(g)
Digraph on 5 vertices
Note that in all cases, we copy the NetworkX structure.
sage: import networkx sage: g = networkx.Graph({0:[1,2,3], 2:[4]}) sage: G = Graph(g, implementation='networkx') sage: H = Graph(g, implementation='networkx') sage: G._backend._nxg is H._backend._nxg False
Returns a dictionary with vertices as the keys and the color class as the values. Fails with an error if the graph is not bipartite.
EXAMPLES:
sage: graphs.CycleGraph(4).bipartite_color()
{0: 1, 1: 0, 2: 1, 3: 0}
sage: graphs.CycleGraph(5).bipartite_color()
...
RuntimeError: Graph is not bipartite.
Returns (X,Y) where X and Y are the nodes in each bipartite set of graph G. Fails with an error if graph is not bipartite.
EXAMPLES:
sage: graphs.CycleGraph(4).bipartite_sets()
(set([0, 2]), set([1, 3]))
sage: graphs.CycleGraph(5).bipartite_sets()
...
RuntimeError: Graph is not bipartite.
Returns the betweenness centrality (fraction of number of shortest paths that go through each vertex) as a dictionary keyed by vertices. The betweenness is normalized by default to be in range (0,1). This wraps NetworkX’s implementation of the algorithm described in [Brandes2003].
Measures of the centrality of a vertex within a graph determine the relative importance of that vertex to its graph. Vertices that occur on more shortest paths between other vertices have higher betweenness than vertices that occur on less.
INPUT:
REFERENCE:
| [Brandes2003] | Ulrik Brandes. (2003). Faster Evaluation of Shortest-Path Based Centrality Indices. [Online] Available: http://citeseer.nj.nec.com/brandes00faster.html |
EXAMPLES:
sage: (graphs.ChvatalGraph()).centrality_betweenness()
{0: 0.069696969696969688, 1: 0.069696969696969688, 2: 0.060606060606060601, 3: 0.060606060606060601, 4: 0.069696969696969688, 5: 0.069696969696969688, 6: 0.060606060606060601, 7: 0.060606060606060601, 8: 0.060606060606060601, 9: 0.060606060606060601, 10: 0.060606060606060601, 11: 0.060606060606060601}
sage: (graphs.ChvatalGraph()).centrality_betweenness(normalized=False)
{0: 7.6666666666666661, 1: 7.6666666666666661, 2: 6.6666666666666661, 3: 6.6666666666666661, 4: 7.6666666666666661, 5: 7.6666666666666661, 6: 6.6666666666666661, 7: 6.6666666666666661, 8: 6.6666666666666661, 9: 6.6666666666666661, 10: 6.6666666666666661, 11: 6.6666666666666661}
sage: D = DiGraph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: D.show(figsize=[2,2])
sage: D = D.to_undirected()
sage: D.show(figsize=[2,2])
sage: D.centrality_betweenness()
{0: 0.16666666666666666, 1: 0.16666666666666666, 2: 0.0, 3: 0.0}
Returns the closeness centrality (1/average distance to all vertices) as a dictionary of values keyed by vertex. The degree centrality is normalized to be in range (0,1).
Measures of the centrality of a vertex within a graph determine the relative importance of that vertex to its graph. ‘Closeness centrality may be defined as the total graph-theoretic distance of a given vertex from all other vertices... Closeness is an inverse measure of centrality in that a larger value indicates a less central actor while a smaller value indicates a more central actor,’ [Borgatti95].
INPUT:
REFERENCE:
| [Borgatti95] | Stephen P Borgatti. (1995). Centrality and AIDS. [Online] Available: http://www.analytictech.com/networks/centaids.htm |
EXAMPLES:
sage: (graphs.ChvatalGraph()).centrality_closeness()
{0: 0.61111111111111..., 1: 0.61111111111111..., 2: 0.61111111111111..., 3: 0.61111111111111..., 4: 0.61111111111111..., 5: 0.61111111111111..., 6: 0.61111111111111..., 7: 0.61111111111111..., 8: 0.61111111111111..., 9: 0.61111111111111..., 10: 0.61111111111111..., 11: 0.61111111111111...}
sage: D = DiGraph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: D.show(figsize=[2,2])
sage: D = D.to_undirected()
sage: D.show(figsize=[2,2])
sage: D.centrality_closeness()
{0: 1.0, 1: 1.0, 2: 0.75, 3: 0.75}
sage: D.centrality_closeness(v=1)
1.0
Returns the degree centrality (fraction of vertices connected to) as a dictionary of values keyed by vertex. The degree centrality is normalized to be in range (0,1).
Measures of the centrality of a vertex within a graph determine the relative importance of that vertex to its graph. Degree centrality measures the number of links incident upon a vertex.
INPUT:
EXAMPLES:
sage: (graphs.ChvatalGraph()).centrality_degree()
{0: 0.36363636363636365, 1: 0.36363636363636365, 2: 0.36363636363636365, 3: 0.36363636363636365, 4: 0.36363636363636365, 5: 0.36363636363636365, 6: 0.36363636363636365, 7: 0.36363636363636365, 8: 0.36363636363636365, 9: 0.36363636363636365, 10: 0.36363636363636365, 11: 0.36363636363636365}
sage: D = DiGraph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: D.show(figsize=[2,2])
sage: D = D.to_undirected()
sage: D.show(figsize=[2,2])
sage: D.centrality_degree()
{0: 1.0, 1: 1.0, 2: 0.66666666666666663, 3: 0.66666666666666663}
sage: D.centrality_degree(v=1)
1.0
Returns the minimal number of colors needed to color the vertices
of the graph  .
.
INPUT:
See also
For more functions related to graph coloring, see the module sage.graphs.graph_coloring.
EXAMPLES:
sage: G = Graph({0: [1, 2, 3], 1: [2]})
sage: G.chromatic_number(algorithm="DLX")
3
sage: G.chromatic_number(algorithm="MILP")
3
sage: G.chromatic_number(algorithm="CP")
3
TESTS:
sage: G = Graph({0: [1, 2, 3], 1: [2]})
sage: G.chromatic_number(algorithm="foo")
...
ValueError: The 'algorithm' keyword must be set to either 'DLX', 'MILP' or 'CP'.
Returns the chromatic polynomial of the graph G.
EXAMPLES:
sage: G = Graph({0:[1,2,3],1:[2]})
sage: factor(G.chromatic_polynomial())
(x - 2) * x * (x - 1)^2
sage: g = graphs.trees(5).next()
sage: g.chromatic_polynomial().factor()
x * (x - 1)^4
sage: seven_acre_wood = sum(graphs.trees(7), Graph())
sage: seven_acre_wood.chromatic_polynomial()
x^77 - 66*x^76 ... - 2515943049305400*x^60 ... - 66*x^12 + x^11
sage: for i in range(2,7):
... graphs.CompleteGraph(i).chromatic_polynomial().factor()
(x - 1) * x
(x - 2) * (x - 1) * x
(x - 3) * (x - 2) * (x - 1) * x
(x - 4) * (x - 3) * (x - 2) * (x - 1) * x
(x - 5) * (x - 4) * (x - 3) * (x - 2) * (x - 1) * x
Returns the clique complex of self. This is the largest simplicial complex on the vertices of self whose 1-skeleton is self.
This is only makes sense for undirected simple graphs.
EXAMPLES:
sage: g = Graph({0:[1,2],1:[2],4:[]})
sage: g.clique_complex()
Simplicial complex with vertex set (0, 1, 2, 4) and facets {(4,), (0, 1, 2)}
sage: h = Graph({0:[1,2,3,4],1:[2,3,4],2:[3]})
sage: x = h.clique_complex()
sage: x
Simplicial complex with vertex set (0, 1, 2, 3, 4) and facets {(0, 1, 4), (0, 1, 2, 3)}
sage: i = x.graph()
sage: i==h
True
sage: x==i.clique_complex()
True
Returns the vertex set of a maximal order complete subgraph.
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
ALGORITHM:
This function is based on Cliquer [NisOst2003].
EXAMPLES:
sage: C=graphs.PetersenGraph()
sage: C.clique_maximum()
[7, 9]
sage: C = Graph('DJ{')
sage: C.clique_maximum()
[1, 2, 3, 4]
Returns the order of the largest clique of the graph (the clique number).
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
INPUT:
- algorithm - either cliquer or networkx
- cliquer - This wraps the C program Cliquer [NisOst2003].
- networkx - This function is based on NetworkX’s implementation of the Bron and Kerbosch Algorithm [BroKer1973].
- cliques - an optional list of cliques that can be input if already computed. Ignored unless algorithm=='networkx'.
ALGORITHM:
This function is based on Cliquer [NisOst2003] and [BroKer1973].
EXAMPLES:
sage: C = Graph('DJ{')
sage: C.clique_number()
4
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.clique_number()
3
(Deprecated) alias for cliques_maximal. See that function for more details.
EXAMPLE:
sage: C = Graph('DJ{')
sage: C.cliques()
doctest:...: DeprecationWarning: The function 'cliques' has been deprecated. Use 'cliques_maximal' or 'cliques_maximum'.
[[4, 0], [4, 1, 2, 3]]
Returns the cliques containing each vertex, represented as a list of lists. (Returns a single list if only one input vertex).
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
INPUT:
EXAMPLES:
sage: C = Graph('DJ{')
sage: C.cliques_containing_vertex()
[[[4, 0]], [[4, 1, 2, 3]], [[4, 1, 2, 3]], [[4, 1, 2, 3]], [[4, 0], [4, 1, 2, 3]]]
sage: E = C.cliques_maximal()
sage: E
[[4, 0], [4, 1, 2, 3]]
sage: C.cliques_containing_vertex(cliques=E)
[[[4, 0]], [[4, 1, 2, 3]], [[4, 1, 2, 3]], [[4, 1, 2, 3]], [[4, 0], [4, 1, 2, 3]]]
sage: F = graphs.Grid2dGraph(2,3)
sage: X = F.cliques_containing_vertex(with_labels=True)
sage: for v in sorted(X.iterkeys()):
... print v, X[v]
(0, 0) [[(0, 1), (0, 0)], [(1, 0), (0, 0)]]
(0, 1) [[(0, 1), (0, 0)], [(0, 1), (0, 2)], [(0, 1), (1, 1)]]
(0, 2) [[(0, 1), (0, 2)], [(1, 2), (0, 2)]]
(1, 0) [[(1, 0), (0, 0)], [(1, 0), (1, 1)]]
(1, 1) [[(0, 1), (1, 1)], [(1, 2), (1, 1)], [(1, 0), (1, 1)]]
(1, 2) [[(1, 2), (0, 2)], [(1, 2), (1, 1)]]
sage: F.cliques_containing_vertex(vertices=[(0, 1), (1, 2)])
[[[(0, 1), (0, 0)], [(0, 1), (0, 2)], [(0, 1), (1, 1)]], [[(1, 2), (0, 2)], [(1, 2), (1, 1)]]]
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.cliques_containing_vertex()
[[[0, 1, 2], [0, 1, 3]], [[0, 1, 2], [0, 1, 3]], [[0, 1, 2]], [[0, 1, 3]]]
Returns a bipartite graph constructed such that maximal cliques are the right vertices and the left vertices are retained from the given graph. Right and left vertices are connected if the bottom vertex belongs to the clique represented by a top vertex.
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
EXAMPLES:
sage: (graphs.ChvatalGraph()).cliques_get_clique_bipartite()
Bipartite graph on 36 vertices
sage: ((graphs.ChvatalGraph()).cliques_get_clique_bipartite()).show(figsize=[2,2], vertex_size=20, vertex_labels=False)
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.cliques_get_clique_bipartite()
Bipartite graph on 6 vertices
sage: (G.cliques_get_clique_bipartite()).show(figsize=[2,2])
Returns a graph constructed with maximal cliques as vertices, and edges between maximal cliques with common members in the original graph.
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
INPUT:
EXAMPLES:
sage: (graphs.ChvatalGraph()).cliques_get_max_clique_graph()
Graph on 24 vertices
sage: ((graphs.ChvatalGraph()).cliques_get_max_clique_graph()).show(figsize=[2,2], vertex_size=20, vertex_labels=False)
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.cliques_get_max_clique_graph()
Graph on 2 vertices
sage: (G.cliques_get_max_clique_graph()).show(figsize=[2,2])
Returns the list of all maximal cliques, with each clique represented by a list of vertices. A clique is an induced complete subgraph, and a maximal clique is one not contained in a larger one.
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
ALGORITHM:
This function is based on NetworkX’s implementation of the Bron and Kerbosch Algorithm [BroKer1973].
REFERENCE:
| [BroKer1973] | (1, 2, 3, 4) Coen Bron and Joep Kerbosch. (1973). Algorithm 457: Finding All Cliques of an Undirected Graph. Commun. ACM. v 16. n 9. pages 575-577. ACM Press. [Online] Available: http://www.ram.org/computing/rambin/rambin.html |
EXAMPLES:
sage: graphs.ChvatalGraph().cliques_maximal()
[[0, 1], [0, 4], [0, 6], [0, 9], [2, 1], [2, 3], [2, 6], [2, 8], [3, 4], [3, 7], [3, 9], [5, 1], [5, 4], [5, 10], [5, 11], [7, 1], [7, 8], [7, 11], [8, 4], [8, 10], [10, 6], [10, 9], [11, 6], [11, 9]]
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.cliques_maximal()
[[0, 1, 2], [0, 1, 3]]
sage: C=graphs.PetersenGraph()
sage: C.cliques_maximal()
[[0, 1], [0, 4], [0, 5], [2, 1], [2, 3], [2, 7], [3, 4], [3, 8], [6, 1], [6, 8], [6, 9], [7, 5], [7, 9], [8, 5], [9, 4]]
sage: C = Graph('DJ{')
sage: C.cliques_maximal()
[[4, 0], [4, 1, 2, 3]]
Returns the list of all maximum cliques, with each clique represented by a list of vertices. A clique is an induced complete subgraph, and a maximum clique is one of maximal order.
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
ALGORITHM:
This function is based on Cliquer [NisOst2003].
REFERENCE:
| [NisOst2003] | (1, 2, 3, 4, 5, 6) Sampo Niskanen and Patric R. J. Ostergard, “Cliquer User’s Guide, Version 1.0,” Communications Laboratory, Helsinki University of Technology, Espoo, Finland, Tech. Rep. T48, 2003. |
EXAMPLES:
sage: graphs.ChvatalGraph().cliques_maximum()
[[0, 1], [0, 4], [0, 6], [0, 9], [1, 2], [1, 5], [1, 7], [2, 3], [2, 6], [2, 8], [3, 4], [3, 7], [3, 9], [4, 5], [4, 8], [5, 10], [5, 11], [6, 10], [6, 11], [7, 8], [7, 11], [8, 10], [9, 10], [9, 11]]
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.cliques_maximum()
[[0, 1, 2], [0, 1, 3]]
sage: C=graphs.PetersenGraph()
sage: C.cliques_maximum()
[[0, 1], [0, 4], [0, 5], [1, 2], [1, 6], [2, 3], [2, 7], [3, 4], [3, 8], [4, 9], [5, 7], [5, 8], [6, 8], [6, 9], [7, 9]]
sage: C = Graph('DJ{')
sage: C.cliques_maximum()
[[1, 2, 3, 4]]
Returns a list of the number of maximal cliques containing each vertex. (Returns a single value if only one input vertex).
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
INPUT:
EXAMPLES:
sage: C = Graph('DJ{')
sage: C.cliques_number_of()
[1, 1, 1, 1, 2]
sage: E = C.cliques_maximal()
sage: E
[[4, 0], [4, 1, 2, 3]]
sage: C.cliques_number_of(cliques=E)
[1, 1, 1, 1, 2]
sage: F = graphs.Grid2dGraph(2,3)
sage: X = F.cliques_number_of(with_labels=True)
sage: for v in sorted(X.iterkeys()):
... print v, X[v]
(0, 0) 2
(0, 1) 3
(0, 2) 2
(1, 0) 2
(1, 1) 3
(1, 2) 2
sage: F.cliques_number_of(vertices=[(0, 1), (1, 2)])
[3, 2]
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.cliques_number_of()
[2, 2, 1, 1]
Returns a list of sizes of the largest maximal cliques containing each vertex. (Returns a single value if only one input vertex).
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
INPUT:
algorithm - either cliquer or networkx
cliquer - This wraps the C program Cliquer [NisOst2003].
- networkx - This function is based on NetworkX’s implementation
of the Bron and Kerbosch Algorithm [BroKer1973].
EXAMPLES:
sage: C = Graph('DJ{')
sage: C.cliques_vertex_clique_number()
[2, 4, 4, 4, 4]
sage: E = C.cliques_maximal()
sage: E
[[4, 0], [4, 1, 2, 3]]
sage: C.cliques_vertex_clique_number(cliques=E,algorithm="networkx")
[2, 4, 4, 4, 4]
sage: F = graphs.Grid2dGraph(2,3)
sage: X = F.cliques_vertex_clique_number(with_labels=True,algorithm="networkx")
sage: for v in sorted(X.iterkeys()):
... print v, X[v]
(0, 0) 2
(0, 1) 2
(0, 2) 2
(1, 0) 2
(1, 1) 2
(1, 2) 2
sage: F.cliques_vertex_clique_number(vertices=[(0, 1), (1, 2)])
[2, 2]
sage: G = Graph({0:[1,2,3], 1:[2], 3:[0,1]})
sage: G.show(figsize=[2,2])
sage: G.cliques_vertex_clique_number()
[3, 3, 3, 3]
Returns the first (optimal) proper vertex-coloring found.
INPUT:
See also
For more functions related to graph coloring, see the module sage.graphs.graph_coloring.
EXAMPLES:
sage: G = Graph("Fooba")
sage: P = G.coloring(algorithm="MILP"); P
[[2, 1, 3], [0, 6, 5], [4]]
sage: P = G.coloring(algorithm="DLX"); P
[[1, 2, 3], [0, 5, 6], [4]]
sage: G.plot(partition=P)
sage: H = G.coloring(hex_colors=True, algorithm="MILP")
sage: for c in sorted(H.keys()):
... print c, H[c]
#0000ff [4]
#00ff00 [0, 6, 5]
#ff0000 [2, 1, 3]
sage: H = G.coloring(hex_colors=True, algorithm="DLX")
sage: for c in sorted(H.keys()):
... print c, H[c]
#0000ff [4]
#00ff00 [1, 2, 3]
#ff0000 [0, 5, 6]
sage: G.plot(vertex_colors=H)
TESTS:
sage: G.coloring(algorithm="foo")
...
ValueError: The 'algorithm' keyword must be set to either 'DLX' or 'MILP'.
Returns a degree-constrained subgraph.
Given a graph  and two functions
and two functions 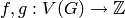 such that
such that 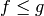 , a degree-constrained subgraph in
, a degree-constrained subgraph in  is
a subgraph
is
a subgraph 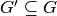 such that for any vertex
such that for any vertex 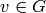 ,
,
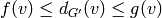 .
.
INPUT:
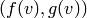 .
.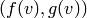 .
.OUTPUT:
Note
EXAMPLES:
Is there a perfect matching in an even cycle?
sage: g = graphs.CycleGraph(6)
sage: bounds = lambda x: [1,1]
sage: m = g.degree_constrained_subgraph(bounds=bounds)
sage: m.size()
3
Return a list of edges forming an eulerian circuit if one exists. Otherwise return False.
This is implemented using Fleury’s algorithm. This could be extended to find eulerian paths too (check for existence and make sure you start on an odd-degree vertex if one exists).
INPUT:
OUTPUT: either ([edges], [vertices]) or [edges] of an Eulerian circuit
EXAMPLES:
sage: g=graphs.CycleGraph(5);
sage: g.eulerian_circuit()
[(0, 1, {}), (1, 2, {}), (2, 3, {}), (3, 4, {}), (4, 0, {})]
sage: g.eulerian_circuit(labels=False)
[(0, 1), (1, 2), (2, 3), (3, 4), (4, 0)]
sage: g = graphs.CompleteGraph(7)
sage: edges, vertices = g.eulerian_circuit(return_vertices=True)
sage: vertices
[0, 1, 2, 0, 3, 1, 4, 0, 5, 1, 6, 2, 3, 4, 2, 5, 3, 6, 4, 5, 6, 0]
sage: graphs.CompleteGraph(4).eulerian_circuit()
False
Returns a Gomory-Hu tree of self.
Given a tree 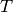 with labeled edges representing capacities, it is very
easy to determine the maximal flow between any pair of vertices :
it is the minimal label on the edges of the unique path between them.
with labeled edges representing capacities, it is very
easy to determine the maximal flow between any pair of vertices :
it is the minimal label on the edges of the unique path between them.
Given a graph  , a Gomory-Hu tree
, a Gomory-Hu tree 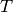 of
of  is a tree
with the same set of vertices, and such that the maximal flow
between any two vertices is the same in
is a tree
with the same set of vertices, and such that the maximal flow
between any two vertices is the same in  as in
as in 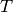 . See the
Wikipedia article on Gomory-Hu tree.
Note that, in general, a graph admits more than one Gomory-Hu tree.
. See the
Wikipedia article on Gomory-Hu tree.
Note that, in general, a graph admits more than one Gomory-Hu tree.
OUTPUT:
graph with labeled edges
EXAMPLE:
Taking the Petersen graph:
sage: g = graphs.PetersenGraph()
sage: t = g.gomory_hu_tree()
Obviously, this graph is a tree:
sage: t.is_tree()
True
Note that if the original graph is not connected, then the Gomory-Hu tree is in fact a forest:
sage: (2*g).gomory_hu_tree().is_forest()
True
sage: (2*g).gomory_hu_tree().is_connected()
False
On the other hand, such a tree has lost nothing of the initial graph connectedness:
sage: all([ t.flow(u,v) == g.flow(u,v) for u,v in Subsets( g.vertices(), 2 ) ])
True
Just to make sure, we can check that the same is true for two vertices in a random graph:
sage: g = graphs.RandomGNP(20,.3)
sage: t = g.gomory_hu_tree()
sage: g.flow(0,1) == t.flow(0,1)
True
And also the min cut:
sage: g.edge_connectivity() == min(t.edge_labels())
True
Returns the graph6 representation of the graph as an ASCII string. Only valid for simple (no loops, multiple edges) graphs on 0 to 262143 vertices.
EXAMPLES:
sage: G = graphs.KrackhardtKiteGraph()
sage: G.graph6_string()
'IvUqwK@?G'
Returns a maximal independent set, which is a set of vertices which induces an empty subgraph. Uses Cliquer [NisOst2003].
Note
Currently only implemented for undirected graphs. Use to_undirected to convert a digraph to an undirected graph.
EXAMPLES:
sage: C=graphs.PetersenGraph()
sage: C.independent_set()
[0, 3, 6, 7]
Returns an independent set of representatives.
Given a graph  and and a family
and and a family ![F=\{F_i:i\in [1,...,k]\}](../../_images/math/1d5e20f47b717d2bf9980de8fff156fa98b19673.png) of
subsets of g.vertices(), an Independent Set of Reprersentatives
(ISR) is an assignation of a vertex
of
subsets of g.vertices(), an Independent Set of Reprersentatives
(ISR) is an assignation of a vertex 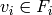 to each set
to each set 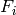 such that
such that 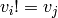 if
if 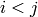 (they are represdentatives) and the
set
(they are represdentatives) and the
set 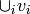 is an independent set in
is an independent set in  .
.
It generalizes, for example, graph coloring and graph list coloring.
(See [AhaBerZiv07] for more information.)
INPUT:
 (actually, a Family of subsets of G.vertices()).
(actually, a Family of subsets of G.vertices()).OUTPUT:
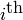 element is the representativeof the
element is the representativeof the
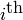 element of the family list. If there is no ISR,
None is returned.
element of the family list. If there is no ISR,
None is returned.EXAMPLES:
For a bipartite graph missing one edge, the solution is as expected:
sage: g = graphs.CompleteBipartiteGraph(3,3)
sage: g.delete_edge(1,4)
sage: g.independent_set_of_representatives([[0,1,2],[3,4,5]])
[1, 4]
The Petersen Graph is 3-colorable, which can be expressed as an independent set of representatives problem : take 3 disjoint copies of the Petersen Graph, each one representing one color. Then take as a partition of the set of vertices the family defined by the three copies of each vertex. The ISR of such a family defines a 3-coloring:
sage: g = 3 * graphs.PetersenGraph()
sage: n = g.order()/3
sage: f = [[i,i+n,i+2*n] for i in xrange(n)]
sage: isr = g.independent_set_of_representatives(f)
sage: c = [floor(i/n) for i in isr]
sage: color_classes = [[],[],[]]
sage: for v,i in enumerate(c):
... color_classes[i].append(v)
sage: for classs in color_classes:
... g.subgraph(classs).size() == 0
True
True
True
REFERENCE:
| [AhaBerZiv07] | R. Aharoni and E. Berger and R. Ziv Independent systems of representatives in weighted graphs Combinatorica vol 27, num 3, p253–267 2007 |
Returns True if graph G is bipartite, False if not.
Traverse the graph G with depth-first-search and color nodes. This function uses the corresponding NetworkX function.
EXAMPLES:
sage: graphs.CycleGraph(4).is_bipartite()
True
sage: graphs.CycleGraph(5).is_bipartite()
False
Since graph is undirected, returns False.
EXAMPLES:
sage: Graph().is_directed()
False
Tests whether self contains an induced even hole.
A Hole is a cycle of length at least 4 (included). It is said to be even (resp. odd) if its length is even (resp. odd).
Even-hole-free graphs always contain a bisimplicial vertex, which ensures that their chromatic number is at most twice their clique number [ABCHRS08].
INPUT:
EXAMPLE:
Is the Petersen Graph even-hole-free
sage: g = graphs.PetersenGraph()
sage: g.is_even_hole_free()
False
As any chordal graph is hole-free, interval graphs behave the same way:
sage: g = graphs.RandomInterval(20)
sage: g.is_even_hole_free()
True
It is clear, though, that a random Bipartite Graph which is not a forest has an even hole:
sage: g = graphs.RandomBipartite(10, 10, .5)
sage: g.is_even_hole_free()
False
We can check the certificate returned is indeed an even cycle:
sage: cycle = g.is_even_hole_free(certificate = True)
sage: cycle.order() % 2 == 0
True
sage: cycle.is_isomorphic(graphs.CycleGraph(cycle.order()))
True
REFERENCE:
| [ABCHRS08] | L. Addario-Berry, M. Chudnovsky, F. Havet, B. Reed, P. Seymour Bisimplicial vertices in even-hole-free graphs Journal of Combinatorial Theory, Series B vol 98, n.6 pp 1119-1164, 2008 |
Tests whether self contains an induced odd hole.
A Hole is a cycle of length at least 4 (included). It is said to be even (resp. odd) if its length is even (resp. odd).
It is interesting to notice that while it is polynomial to check whether a graph has an odd hole or an odd antihole [CRST06], it is not known whether testing for one of these two cases independently is polynomial too.
INPUT:
EXAMPLE:
Is the Petersen Graph odd-hole-free
sage: g = graphs.PetersenGraph()
sage: g.is_odd_hole_free()
False
Which was to be expected, as its girth is 5
sage: g.girth()
5
We can check the certificate returned is indeed a 5-cycle:
sage: cycle = g.is_odd_hole_free(certificate = True)
sage: cycle.is_isomorphic(graphs.CycleGraph(5))
True
As any chordal graph is hole-free, no interval graph has an odd hole:
sage: g = graphs.RandomInterval(20)
sage: g.is_odd_hole_free()
True
REFERENCES:
| [CRST06] | M. Chudnovsky, G. Cornuejols, X. Liu, P. Seymour, K. Vuskovic Recognizing berge graphs Combinatorica vol 25, n 2, pages 143–186 2005 |
Returns True if the graph is a Split graph, False otherwise.
A Graph  is said to be a split graph if its vertices
is said to be a split graph if its vertices 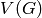 can be partitioned into two sets
can be partitioned into two sets 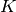 and
and 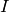 such that the
vertices of
such that the
vertices of 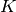 induce a complete graphe, and those of
induce a complete graphe, and those of 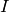 are
an independent set.
are
an independent set.
There is a simple test to check whether a graph is a split graph (see, for instance, the book “Graph Classes, a survey” [GraphClasses] page 203) :
Given the degree sequence 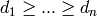 of
of  , a graph
is a split graph if and only if :
, a graph
is a split graph if and only if :
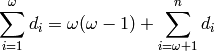
where 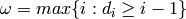 .
.
EXAMPLES:
Split graphs are, in particular, chordal graphs. Hence, The Petersen graph can not be split:
sage: graphs.PetersenGraph().is_split()
False
We can easily build some “random” split graph by creating a complete graph, and adding vertices only connected to some random vertices of the clique:
sage: g = graphs.CompleteGraph(10)
sage: sets = Subsets(Set(range(10)))
sage: for i in range(10, 25):
... g.add_edges([(i,k) for k in sets.random_element()])
sage: g.is_split()
True
REFERENCES:
| [GraphClasses] | A. Brandstadt, VB Le and JP Spinrad Graph classes: a survey SIAM Monographs on Discrete Mathematics and Applications}, 1999 |
Returns whether self is triangle-free
EXAMPLE:
The Petersen Graph is triangle-free:
sage: g = graphs.PetersenGraph()
sage: g.is_triangle_free()
True
or a complete Bipartite Graph:
sage: g = graphs.CompleteBipartiteGraph(5,6)
sage: g.is_triangle_free()
True
a tripartite graph, though, contains many triangles
sage: g = (3 * graphs.CompleteGraph(5)).complement()
sage: g.is_triangle_free()
False
Returns the edges of a minimum spanning tree, if one exists, otherwise returns False.
INPUT:
OUTPUT: the edges of a minimum spanning tree.
EXAMPLES:
sage: g=graphs.CompleteGraph(5)
sage: len(g.min_spanning_tree())
4
sage: weight = lambda e: 1/( (e[0]+1)*(e[1]+1) )
sage: g.min_spanning_tree(weight_function=weight)
[(3, 4, {}), (2, 4, {}), (1, 4, {}), (0, 4, {})]
sage: g.min_spanning_tree(algorithm='Prim edge', starting_vertex=2, weight_function=weight)
[(2, 4, {}), (3, 4, {}), (1, 4, {}), (0, 4, {})]
sage: g.min_spanning_tree(algorithm='Prim fringe', starting_vertex=2, weight_function=weight)
[(2, 4), (4, 3), (4, 1), (4, 0)]
Returns the vertices of a minor isomorphic to 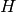 in the current graph.
in the current graph.
We say that a graph  has a
has a 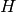 -minor (or that it has
a graph isomorphic to
-minor (or that it has
a graph isomorphic to 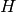 as a minor), if for all
as a minor), if for all 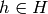 ,
there exist disjoint sets
,
there exist disjoint sets 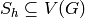 such that
once the vertices of each
such that
once the vertices of each 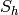 have been merged to create
a new graph
have been merged to create
a new graph 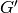 , this new graph contains
, this new graph contains 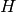 as a subgraph.
as a subgraph.
For more information, see the Wikipedia article on graph minor.
INPUT:
OUTPUT:
A dictionary associating to each vertex of 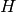 the set of vertices
in the current graph representing it.
the set of vertices
in the current graph representing it.
ALGORITHM:
Mixed Integer Linear Programming
COMPLEXITY:
Theoretically, when 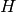 is fixed, testing for the existence of
a
is fixed, testing for the existence of
a 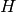 -minor is polynomial. The known algorithms are highly
exponential in
-minor is polynomial. The known algorithms are highly
exponential in 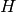 , though.
, though.
Note
This function can be expected to be very slow, especially where the minor does not exist.
EXAMPLES:
Trying to find a minor isomorphic to 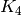 in
the
in
the 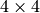 grid:
grid:
sage: g = graphs.GridGraph([4,4])
sage: h = graphs.CompleteGraph(4)
sage: L = g.minor(h)
sage: gg = g.subgraph(flatten(L.values(), max_level = 1))
sage: _ = [gg.merge_vertices(l) for l in L.values() if len(l)>1]
sage: gg.is_isomorphic(h)
True
We can also try to prove this way that the Petersen graph
is not planar, as it has a 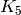 minor:
minor:
sage: g = graphs.PetersenGraph()
sage: K5_minor = g.minor(graphs.CompleteGraph(5)) # long
And even a 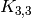 minor:
minor:
sage: K33_minor = g.minor(graphs.CompleteBipartiteGraph(3,3)) # long
(It is much faster to use the linear-time test of planarity in this situation, though.)
As there is no cycle in a tree, looking for a 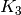 minor is useless.
This function will raise an exception in this case:
minor is useless.
This function will raise an exception in this case:
sage: g = graphs.RandomGNP(20,.5)
sage: g = g.subgraph(edges = g.min_spanning_tree())
sage: g.is_tree()
True
sage: L = g.minor(graphs.CompleteGraph(3))
...
ValueError: This graph has no minor isomorphic to H !
Returns the sparse6 representation of the graph as an ASCII string. Only valid for undirected graphs on 0 to 262143 vertices, but loops and multiple edges are permitted.
EXAMPLES:
sage: G = graphs.BullGraph()
sage: G.sparse6_string()
':Da@en'
sage: G = Graph()
sage: G.sparse6_string()
':?'
sage: G = Graph(loops=True, multiedges=True,sparse=True)
sage: Graph(':?',sparse=True) == G
True
Returns a strongly connected orientation of the current graph. See also the Wikipedia article on strongly connected component.
An orientation of an undirected graph is a digraph obtained by giving an unique direction to each of its edges. An orientation is said to be strong if there is a directed path between each pair of vertices.
If the graph is 2-edge-connected, a strongly connected orientation can be found in linear time. If the given graph is not 2-connected, the orientation returned will ensure that each 2-connected component has a strongly connected orientation.
OUTPUT:
A digraph representing an orientation of the current graph.
Note
EXAMPLE:
For a 2-regular graph, a strong orientation gives to each vertex an out-degree equal to 1:
sage: g = graphs.CycleGraph(5)
sage: g.strong_orientation().out_degree()
[1, 1, 1, 1, 1]
The Petersen Graph is 2-edge connected. It then has a strongly connected orientation:
sage: g = graphs.PetersenGraph()
sage: o = g.strong_orientation()
sage: len(o.strongly_connected_components())
1
The same goes for the CubeGraph in any dimension
sage: for i in range(2,5):
... g = graphs.CubeGraph(i)
... o = g.strong_orientation()
... len(o.strongly_connected_components())
1
1
1
Returns a directed version of the graph. A single edge becomes two edges, one in each direction.
EXAMPLES:
sage: graphs.PetersenGraph().to_directed()
Petersen graph: Digraph on 10 vertices
Since the graph is already undirected, simply returns a copy of itself.
EXAMPLES:
sage: graphs.PetersenGraph().to_undirected()
Petersen graph: Graph on 10 vertices
Returns a decomposition of the graph into 2-factors.
Petersen’s 2-factor decomposition theorem asserts that any
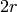 -regular graph
-regular graph  can be decomposed into 2-factors.
Equivalently, it means that the edges of any
can be decomposed into 2-factors.
Equivalently, it means that the edges of any 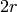 -regular
graphs can be partitionned in
-regular
graphs can be partitionned in  sets
sets 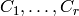 such
that for all
such
that for all  , the set
, the set 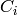 is a disjoint union of cycles
( a 2-regular graph ).
is a disjoint union of cycles
( a 2-regular graph ).
As any graph of maximal degree 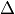 can be completed into
a regular graph of degree
can be completed into
a regular graph of degree 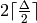 , this
result also means that the edges of any graph of degree
, this
result also means that the edges of any graph of degree 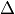 can be partitionned in
can be partitionned in 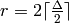 sets
sets
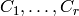 such that for all
such that for all  , the set
, the set 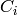 is a
graph of maximal degree
is a
graph of maximal degree 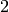 ( a disjoint union of paths
and cycles ).
( a disjoint union of paths
and cycles ).
EXAMPLE:
The Complete Graph on 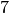 vertices is a
vertices is a 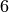 -regular graph, so it can
be edge-partitionned into
-regular graph, so it can
be edge-partitionned into 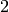 -regular graphs:
-regular graphs:
sage: g = graphs.CompleteGraph(7)
sage: classes = g.two_factor_petersen()
sage: for c in classes:
... gg = Graph()
... gg.add_edges(c)
... print max(gg.degree())<=2
True
True
True
sage: Set(set(classes[0]) | set(classes[1]) | set(classes[2])).cardinality() == g.size()
True
sage: g = graphs.CirculantGraph(24, [7, 11])
sage: cl = g.two_factor_petersen()
sage: g.plot(edge_colors={'black':cl[0], 'red':cl[1]})
Writes a plot of the graph to filename in eps format.
INPUT:
- filename – a string
- **options – same layout options as layout()
EXAMPLES:
sage: P = graphs.PetersenGraph()
sage: P.write_to_eps(tmp_dir() + 'sage.eps')
It is relatively simple to include this file in a LaTeX document. \usepackagegraphics must appear in the preamble, and \includegraphics{filename.eps} will include the file. To compile the document to pdf with pdflatex the file needs first to be converted to pdf, for example with ps2pdf filename.eps filename.pdf.
Compare edge x to edge y, return -1 if x y, 1 if x y, else 0.
EXAMPLES:
sage: G = graphs.PetersenGraph()
sage: E = G.edges()
sage: from sage.graphs.graph import compare_edges
sage: compare_edges(E[0], E[2])
-1
sage: compare_edges(E[0], E[1])
-1
sage: compare_edges(E[0], E[0])
0
sage: compare_edges(E[1], E[0])
1