Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Graph Theory »

This module implements functions and operations involving directed graphs.
Bases: sage.graphs.generic_graph.GenericGraph
Directed graph.
A digraph or directed graph is a set of vertices connected by oriented edges. For more information, see the Wikipedia article on digraphs.
One can very easily create a directed graph in Sage by typing:
sage: g = DiGraph()
By typing the name of the digraph, one can get some basic information about it:
sage: g
Digraph on 0 vertices
This digraph is not very interesting as it is by default the empty graph. But Sage contains several pre-defined digraph classes that can be listed this way:
You will see a list of methods which will construct named digraphs. For example:
sage: g = digraphs.ButterflyGraph(3)
sage: g.plot()
You can also use the collection of pre-defined graphs, then create a digraph from them.
sage: g = DiGraph(graphs.PetersenGraph())
sage: g.plot()
Calling Digraph on a graph returns the original graph in which every edge is replaced by two different edges going toward opposite directions.
In order to obtain more information about these digraph constructors, access the documentation by typing digraphs.RandomDirectedGNP?.
Once you have defined the digraph you want, you can begin to work on it by using the almost 200 functions on graphs and digraphs in the Sage library! If your digraph is named g, you can list these functions as previously this way
As usual, you can get some information about what these functions do by typing (e.g. if you want to know about the diameter() method) g.diameter?.
If you have defined a digraph g having several connected components ( i.e. g.is_connected() returns False ), you can print each one of its connected components with only two lines:
sage: for component in g.connected_components():
... g.subgraph(component).plot()
INPUT:
data - can be any of the following:
pos - a positioning dictionary: for example, the spring layout from NetworkX for the 5-cycle is:
{0: [-0.91679746, 0.88169588],
1: [ 0.47294849, 1.125 ],
2: [ 1.125 ,-0.12867615],
3: [ 0.12743933,-1.125 ],
4: [-1.125 ,-0.50118505]}
name - (must be an explicitly named parameter, i.e., name=”complete”) gives the graph a name
loops - boolean, whether to allow loops (ignored if data is an instance of the DiGraph class)
multiedges - boolean, whether to allow multiple edges (ignored if data is an instance of the DiGraph class)
weighted - whether digraph thinks of itself as weighted or not. See self.weighted()
format - if None, DiGraph tries to guess- can be several values, including:
boundary - a list of boundary vertices, if none, digraph is considered as a ‘digraph without boundary’
implementation - what to use as a backend for the graph. Currently, the options are either ‘networkx’ or ‘c_graph’
sparse - only for implementation == ‘c_graph’. Whether to use sparse or dense graphs as backend. Note that currently dense graphs do not have edge labels, nor can they be multigraphs
vertex_labels - only for implementation == ‘c_graph’. Whether to allow any object as a vertex (slower), or only the integers 0, ..., n-1, where n is the number of vertices.
EXAMPLES:
A dictionary of dictionaries:
sage: g = DiGraph({0:{1:'x',2:'z',3:'a'}, 2:{5:'out'}}); g
Digraph on 5 vertices
The labels (‘x’, ‘z’, ‘a’, ‘out’) are labels for edges. For example, ‘out’ is the label for the edge from 2 to 5. Labels can be used as weights, if all the labels share some common parent.
A dictionary of lists:
sage: g = DiGraph({0:[1,2,3], 2:[4]}); g
Digraph on 5 vertices
A list of vertices and a function describing adjacencies. Note that the list of vertices and the function must be enclosed in a list (i.e., [list of vertices, function]).
We construct a graph on the integers 1 through 12 such that there is a directed edge from i to j if and only if i divides j.
sage: g=DiGraph([[1..12],lambda i,j: i!=j and i.divides(j)])
sage: g.vertices()
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
sage: g.adjacency_matrix()
[0 1 1 1 1 1 1 1 1 1 1 1]
[0 0 0 1 0 1 0 1 0 1 0 1]
[0 0 0 0 0 1 0 0 1 0 0 1]
[0 0 0 0 0 0 0 1 0 0 0 1]
[0 0 0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 0 0 0 1]
[0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0]
A numpy matrix or ndarray:
sage: import numpy
sage: A = numpy.array([[0,1,0],[1,0,0],[1,1,0]])
sage: DiGraph(A)
Digraph on 3 vertices
A Sage matrix: Note: If format is not specified, then Sage assumes a square matrix is an adjacency matrix, and a nonsquare matrix is an incidence matrix.
an adjacency matrix:
sage: M = Matrix([[0, 1, 1, 1, 0],[0, 0, 0, 0, 0],[0, 0, 0, 0, 1],[0, 0, 0, 0, 0],[0, 0, 0, 0, 0]]); M
[0 1 1 1 0]
[0 0 0 0 0]
[0 0 0 0 1]
[0 0 0 0 0]
[0 0 0 0 0]
sage: DiGraph(M)
Digraph on 5 vertices
an incidence matrix:
sage: M = Matrix(6, [-1,0,0,0,1, 1,-1,0,0,0, 0,1,-1,0,0, 0,0,1,-1,0, 0,0,0,1,-1, 0,0,0,0,0]); M
[-1 0 0 0 1]
[ 1 -1 0 0 0]
[ 0 1 -1 0 0]
[ 0 0 1 -1 0]
[ 0 0 0 1 -1]
[ 0 0 0 0 0]
sage: DiGraph(M)
Digraph on 6 vertices
A c_graph implemented DiGraph can be constructed from a networkx implemented DiGraph:
sage: D = DiGraph({0:[1],1:[2],2:[0]}, implementation="networkx")
sage: E = DiGraph(D,implementation="c_graph")
sage: D == E
True
A dig6 string: Sage automatically recognizes whether a string is in dig6 format, which is a directed version of graph6:
sage: D = DiGraph('IRAaDCIIOWEOKcPWAo')
sage: D
Digraph on 10 vertices
sage: D = DiGraph('IRAaDCIIOEOKcPWAo')
...
RuntimeError: The string (IRAaDCIIOEOKcPWAo) seems corrupt: for n = 10, the string is too short.
sage: D = DiGraph("IRAaDCI'OWEOKcPWAo")
...
RuntimeError: The string seems corrupt: valid characters are
?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~
A NetworkX XDiGraph:
sage: import networkx
sage: g = networkx.MultiDiGraph({0:[1,2,3], 2:[4]})
sage: DiGraph(g)
Digraph on 5 vertices
A NetworkX digraph:
sage: import networkx
sage: g = networkx.DiGraph({0:[1,2,3], 2:[4]})
sage: DiGraph(g)
Digraph on 5 vertices
Note that in all cases, we copy the NetworkX structure.
sage: import networkx
sage: g = networkx.DiGraph({0:[1,2,3], 2:[4]})
sage: G = DiGraph(g, implementation='networkx')
sage: H = DiGraph(g, implementation='networkx')
sage: G._backend._nxg is H._backend._nxg
False
Returns an iterator over all the cycles of self starting with one of the given vertices. The cycles are enumerated in increasing length order.
INPUT:
OUTPUT:
iterator
Note
See also all_simple_cycles(...).
AUTHOR:
Alexandre Blondin Masse
EXAMPLES:
sage: g = DiGraph({'a' : ['a', 'b'], 'b' : ['c'], 'c' : ['d'], 'd' : ['c']}, loops=True)
sage: it = g.all_cycles_iterator()
sage: for _ in range(7): print it.next()
['a', 'a']
['a', 'a', 'a']
['c', 'd', 'c']
['a', 'a', 'a', 'a']
['a', 'a', 'a', 'a', 'a']
['c', 'd', 'c', 'd', 'c']
['a', 'a', 'a', 'a', 'a', 'a']
There are no cycles in the empty graph and in acyclic graphs:
sage: g = DiGraph()
sage: it = g.all_cycles_iterator()
sage: list(it)
[]
sage: g = DiGraph({0:[1]})
sage: it = g.all_cycles_iterator()
sage: list(it)
[]
It is possible to restrict the starting vertices of the cycles:
sage: g = DiGraph({'a' : ['a', 'b'], 'b' : ['c'], 'c' : ['d'], 'd' : ['c']}, loops=True)
sage: it = g.all_cycles_iterator(starting_vertices=['b', 'c'])
sage: for _ in range(3): print it.next()
['c', 'd', 'c']
['c', 'd', 'c', 'd', 'c']
['c', 'd', 'c', 'd', 'c', 'd', 'c']
Also, one can bound the length of the cycles:
sage: it = g.all_cycles_iterator(max_length=3)
sage: list(it)
[['a', 'a'], ['a', 'a', 'a'], ['c', 'd', 'c'], ['a', 'a', 'a', 'a']]
By default, cycles differing only by their starting point are not all enumerated, but this may be parametrized:
sage: it = g.all_cycles_iterator(max_length=3, rooted=False)
sage: list(it)
[['a', 'a'], ['a', 'a', 'a'], ['c', 'd', 'c'], ['a', 'a', 'a', 'a']]
sage: it = g.all_cycles_iterator(max_length=3, rooted=True)
sage: list(it)
[['a', 'a'], ['a', 'a', 'a'], ['c', 'd', 'c'], ['d', 'c', 'd'], ['a', 'a', 'a', 'a']]
One may prefer to enumerate simple cycles, i.e. cycles such that the only vertex occuring twice in it is the starting and ending one (see also all_simple_cycles(...):
sage: it = g.all_cycles_iterator(simple=True)
sage: list(it)
[['a', 'a'], ['c', 'd', 'c']]
sage: g = digraphs.Circuit(4)
sage: list(g.all_cycles_iterator(simple=True))
[[0, 1, 2, 3, 0]]
Returns an iterator over the paths of self. The paths are enumerated in increasing length order.
INPUT:
OUTPUT:
iterator
AUTHOR:
Alexandre Blondin Masse
EXAMPLES:
sage: g = DiGraph({'a' : ['a', 'b'], 'b' : ['c'], 'c' : ['d'], 'd' : ['c']}, loops=True)
sage: pi = g.all_paths_iterator()
sage: for _ in range(7): print pi.next()
['a', 'a']
['a', 'b']
['b', 'c']
['c', 'd']
['d', 'c']
['a', 'a', 'a']
['a', 'a', 'b']
It is possible to precise the allowed starting and/or ending vertices:
sage: pi = g.all_paths_iterator(starting_vertices=['a'])
sage: for _ in range(5): print pi.next()
['a', 'a']
['a', 'b']
['a', 'a', 'a']
['a', 'a', 'b']
['a', 'b', 'c']
sage: pi = g.all_paths_iterator(starting_vertices=['a'], ending_vertices=['b'])
sage: for _ in range(5): print pi.next()
['a', 'b']
['a', 'a', 'b']
['a', 'a', 'a', 'b']
['a', 'a', 'a', 'a', 'b']
['a', 'a', 'a', 'a', 'a', 'b']
One may prefer to enumerate only simple paths (see all_simple_paths(...)):
sage: pi = g.all_paths_iterator(simple=True)
sage: list(pi)
[['a', 'a'], ['a', 'b'], ['b', 'c'], ['c', 'd'], ['d', 'c'], ['a', 'b', 'c'], ['b', 'c', 'd'], ['c', 'd', 'c'], ['d', 'c', 'd'], ['a', 'b', 'c', 'd'], ['b', 'c', 'd', 'c'], ['a', 'b', 'c', 'd', 'c']]
Or simply bound the length of the enumerated paths:
sage: pi = g.all_paths_iterator(starting_vertices=['a'], ending_vertices=['b', 'c'], max_length=6)
sage: list(pi)
[['a', 'b'], ['a', 'a', 'b'], ['a', 'b', 'c'], ['a', 'a', 'a', 'b'], ['a', 'a', 'b', 'c'], ['a', 'a', 'a', 'a', 'b'], ['a', 'a', 'a', 'b', 'c'], ['a', 'b', 'c', 'd', 'c'], ['a', 'a', 'a', 'a', 'a', 'b'], ['a', 'a', 'a', 'a', 'b', 'c'], ['a', 'a', 'b', 'c', 'd', 'c'], ['a', 'a', 'a', 'a', 'a', 'a', 'b'], ['a', 'a', 'a', 'a', 'a', 'b', 'c'], ['a', 'a', 'a', 'b', 'c', 'd', 'c'], ['a', 'b', 'c', 'd', 'c', 'd', 'c']]
By default, empty paths are not enumerated, but it may be parametrized:
sage: pi = g.all_paths_iterator(simple=True, trivial=True)
sage: list(pi)
[['a'], ['b'], ['c'], ['d'], ['a', 'a'], ['a', 'b'], ['b', 'c'], ['c', 'd'], ['d', 'c'], ['a', 'b', 'c'], ['b', 'c', 'd'], ['c', 'd', 'c'], ['d', 'c', 'd'], ['a', 'b', 'c', 'd'], ['b', 'c', 'd', 'c'], ['a', 'b', 'c', 'd', 'c']]
sage: pi = g.all_paths_iterator(simple=True, trivial=False)
sage: list(pi)
[['a', 'a'], ['a', 'b'], ['b', 'c'], ['c', 'd'], ['d', 'c'], ['a', 'b', 'c'], ['b', 'c', 'd'], ['c', 'd', 'c'], ['d', 'c', 'd'], ['a', 'b', 'c', 'd'], ['b', 'c', 'd', 'c'], ['a', 'b', 'c', 'd', 'c']]
Returns a list of all simple cycles of self.
INPUT:
OUTPUT:
list
Note
Although the number of simple cycles of a finite graph is always finite, computing all its cycle may take a very long time.
EXAMPLES:
sage: g = DiGraph({'a' : ['a', 'b'], 'b' : ['c'], 'c' : ['d'], 'd' : ['c']}, loops=True)
sage: g.all_simple_cycles()
[['a', 'a'], ['c', 'd', 'c']]
The directed version of the Petersen graph:
sage: g = graphs.PetersenGraph().to_directed()
sage: g.all_simple_cycles(max_length=4)
[[0, 1, 0], [0, 4, 0], [0, 5, 0], [1, 2, 1], [1, 6, 1], [2, 3, 2], [2, 7, 2], [3, 8, 3], [3, 4, 3], [4, 9, 4], [5, 8, 5], [5, 7, 5], [6, 8, 6], [6, 9, 6], [7, 9, 7]]
sage: g.all_simple_cycles(max_length=6)
[[0, 1, 0], [0, 4, 0], [0, 5, 0], [1, 2, 1], [1, 6, 1], [2, 3, 2], [2, 7, 2], [3, 8, 3], [3, 4, 3], [4, 9, 4], [5, 8, 5], [5, 7, 5], [6, 8, 6], [6, 9, 6], [7, 9, 7], [0, 1, 2, 3, 4, 0], [0, 1, 2, 7, 5, 0], [0, 1, 6, 8, 5, 0], [0, 1, 6, 9, 4, 0], [0, 4, 9, 6, 1, 0], [0, 4, 9, 7, 5, 0], [0, 4, 3, 8, 5, 0], [0, 4, 3, 2, 1, 0], [0, 5, 8, 3, 4, 0], [0, 5, 8, 6, 1, 0], [0, 5, 7, 9, 4, 0], [0, 5, 7, 2, 1, 0], [1, 2, 3, 8, 6, 1], [1, 2, 7, 9, 6, 1], [1, 6, 8, 3, 2, 1], [1, 6, 9, 7, 2, 1], [2, 3, 8, 5, 7, 2], [2, 3, 4, 9, 7, 2], [2, 7, 9, 4, 3, 2], [2, 7, 5, 8, 3, 2], [3, 8, 6, 9, 4, 3], [3, 4, 9, 6, 8, 3], [5, 8, 6, 9, 7, 5], [5, 7, 9, 6, 8, 5], [0, 1, 2, 3, 8, 5, 0], [0, 1, 2, 7, 9, 4, 0], [0, 1, 6, 8, 3, 4, 0], [0, 1, 6, 9, 7, 5, 0], [0, 4, 9, 6, 8, 5, 0], [0, 4, 9, 7, 2, 1, 0], [0, 4, 3, 8, 6, 1, 0], [0, 4, 3, 2, 7, 5, 0], [0, 5, 8, 3, 2, 1, 0], [0, 5, 8, 6, 9, 4, 0], [0, 5, 7, 9, 6, 1, 0], [0, 5, 7, 2, 3, 4, 0], [1, 2, 3, 4, 9, 6, 1], [1, 2, 7, 5, 8, 6, 1], [1, 6, 8, 5, 7, 2, 1], [1, 6, 9, 4, 3, 2, 1], [2, 3, 8, 6, 9, 7, 2], [2, 7, 9, 6, 8, 3, 2], [3, 8, 5, 7, 9, 4, 3], [3, 4, 9, 7, 5, 8, 3]]
The complete graph (without loops) on 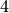 vertices:
vertices:
sage: g = graphs.CompleteGraph(4).to_directed()
sage: g.all_simple_cycles()
[[0, 1, 0], [0, 2, 0], [0, 3, 0], [1, 2, 1], [1, 3, 1], [2, 3, 2], [0, 1, 2, 0], [0, 1, 3, 0], [0, 2, 1, 0], [0, 2, 3, 0], [0, 3, 1, 0], [0, 3, 2, 0], [1, 2, 3, 1], [1, 3, 2, 1], [0, 1, 2, 3, 0], [0, 1, 3, 2, 0], [0, 2, 1, 3, 0], [0, 2, 3, 1, 0], [0, 3, 1, 2, 0], [0, 3, 2, 1, 0]]
If the graph contains a large number of cycles, one can bound the length of the cycles, or simply restrict the possible starting vertices of the cycles:
sage: g = graphs.CompleteGraph(20).to_directed()
sage: g.all_simple_cycles(max_length=2)
[[0, 1, 0], [0, 2, 0], [0, 3, 0], [0, 4, 0], [0, 5, 0], [0, 6, 0], [0, 7, 0], [0, 8, 0], [0, 9, 0], [0, 10, 0], [0, 11, 0], [0, 12, 0], [0, 13, 0], [0, 14, 0], [0, 15, 0], [0, 16, 0], [0, 17, 0], [0, 18, 0], [0, 19, 0], [1, 2, 1], [1, 3, 1], [1, 4, 1], [1, 5, 1], [1, 6, 1], [1, 7, 1], [1, 8, 1], [1, 9, 1], [1, 10, 1], [1, 11, 1], [1, 12, 1], [1, 13, 1], [1, 14, 1], [1, 15, 1], [1, 16, 1], [1, 17, 1], [1, 18, 1], [1, 19, 1], [2, 3, 2], [2, 4, 2], [2, 5, 2], [2, 6, 2], [2, 7, 2], [2, 8, 2], [2, 9, 2], [2, 10, 2], [2, 11, 2], [2, 12, 2], [2, 13, 2], [2, 14, 2], [2, 15, 2], [2, 16, 2], [2, 17, 2], [2, 18, 2], [2, 19, 2], [3, 4, 3], [3, 5, 3], [3, 6, 3], [3, 7, 3], [3, 8, 3], [3, 9, 3], [3, 10, 3], [3, 11, 3], [3, 12, 3], [3, 13, 3], [3, 14, 3], [3, 15, 3], [3, 16, 3], [3, 17, 3], [3, 18, 3], [3, 19, 3], [4, 5, 4], [4, 6, 4], [4, 7, 4], [4, 8, 4], [4, 9, 4], [4, 10, 4], [4, 11, 4], [4, 12, 4], [4, 13, 4], [4, 14, 4], [4, 15, 4], [4, 16, 4], [4, 17, 4], [4, 18, 4], [4, 19, 4], [5, 6, 5], [5, 7, 5], [5, 8, 5], [5, 9, 5], [5, 10, 5], [5, 11, 5], [5, 12, 5], [5, 13, 5], [5, 14, 5], [5, 15, 5], [5, 16, 5], [5, 17, 5], [5, 18, 5], [5, 19, 5], [6, 7, 6], [6, 8, 6], [6, 9, 6], [6, 10, 6], [6, 11, 6], [6, 12, 6], [6, 13, 6], [6, 14, 6], [6, 15, 6], [6, 16, 6], [6, 17, 6], [6, 18, 6], [6, 19, 6], [7, 8, 7], [7, 9, 7], [7, 10, 7], [7, 11, 7], [7, 12, 7], [7, 13, 7], [7, 14, 7], [7, 15, 7], [7, 16, 7], [7, 17, 7], [7, 18, 7], [7, 19, 7], [8, 9, 8], [8, 10, 8], [8, 11, 8], [8, 12, 8], [8, 13, 8], [8, 14, 8], [8, 15, 8], [8, 16, 8], [8, 17, 8], [8, 18, 8], [8, 19, 8], [9, 10, 9], [9, 11, 9], [9, 12, 9], [9, 13, 9], [9, 14, 9], [9, 15, 9], [9, 16, 9], [9, 17, 9], [9, 18, 9], [9, 19, 9], [10, 11, 10], [10, 12, 10], [10, 13, 10], [10, 14, 10], [10, 15, 10], [10, 16, 10], [10, 17, 10], [10, 18, 10], [10, 19, 10], [11, 12, 11], [11, 13, 11], [11, 14, 11], [11, 15, 11], [11, 16, 11], [11, 17, 11], [11, 18, 11], [11, 19, 11], [12, 13, 12], [12, 14, 12], [12, 15, 12], [12, 16, 12], [12, 17, 12], [12, 18, 12], [12, 19, 12], [13, 14, 13], [13, 15, 13], [13, 16, 13], [13, 17, 13], [13, 18, 13], [13, 19, 13], [14, 15, 14], [14, 16, 14], [14, 17, 14], [14, 18, 14], [14, 19, 14], [15, 16, 15], [15, 17, 15], [15, 18, 15], [15, 19, 15], [16, 17, 16], [16, 18, 16], [16, 19, 16], [17, 18, 17], [17, 19, 17], [18, 19, 18]]
sage: g = graphs.CompleteGraph(20).to_directed()
sage: g.all_simple_cycles(max_length=2, starting_vertices=[0])
[[0, 1, 0], [0, 2, 0], [0, 3, 0], [0, 4, 0], [0, 5, 0], [0, 6, 0], [0, 7, 0], [0, 8, 0], [0, 9, 0], [0, 10, 0], [0, 11, 0], [0, 12, 0], [0, 13, 0], [0, 14, 0], [0, 15, 0], [0, 16, 0], [0, 17, 0], [0, 18, 0], [0, 19, 0]]
One may prefer to distinguish equivalent cycles having distinct starting vertices (compare the following examples):
sage: g = graphs.CompleteGraph(4).to_directed()
sage: g.all_simple_cycles(max_length=2, rooted=False)
[[0, 1, 0], [0, 2, 0], [0, 3, 0], [1, 2, 1], [1, 3, 1], [2, 3, 2]]
sage: g.all_simple_cycles(max_length=2, rooted=True)
[[0, 1, 0], [0, 2, 0], [0, 3, 0], [1, 0, 1], [1, 2, 1], [1, 3, 1], [2, 0, 2], [2, 1, 2], [2, 3, 2], [3, 0, 3], [3, 1, 3], [3, 2, 3]]
Returns a list of all the simple paths of self starting with one of the given vertices. A path is simple if no vertex occurs twice in it except possibly the starting and ending one. The paths are enumerated in increasing length order.
INPUT:
OUTPUT:
list
Note
Although the number of simple paths of a finite graph is always finite, computing all its paths may take a very long time.
EXAMPLES:
sage: g = DiGraph({'a' : ['a', 'b'], 'b' : ['c'], 'c' : ['d'], 'd' : ['c']}, loops=True)
sage: g.all_simple_paths()
[['a', 'a'], ['a', 'b'], ['b', 'c'], ['c', 'd'], ['d', 'c'], ['a', 'b', 'c'], ['b', 'c', 'd'], ['c', 'd', 'c'], ['d', 'c', 'd'], ['a', 'b', 'c', 'd'], ['b', 'c', 'd', 'c'], ['a', 'b', 'c', 'd', 'c']]
One may compute all paths having specific starting and/or ending vertices:
sage: g.all_simple_paths(starting_vertices=['a'])
[['a', 'a'], ['a', 'b'], ['a', 'b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b', 'c', 'd', 'c']]
sage: g.all_simple_paths(starting_vertices=['a'], ending_vertices=['c'])
[['a', 'b', 'c'], ['a', 'b', 'c', 'd', 'c']]
sage: g.all_simple_paths(starting_vertices=['a'], ending_vertices=['b', 'c'])
[['a', 'b'], ['a', 'b', 'c'], ['a', 'b', 'c', 'd', 'c']]
It is also possible to bound the length of the paths:
sage: g.all_simple_paths(max_length=2)
[['a', 'a'], ['a', 'b'], ['b', 'c'], ['c', 'd'], ['d', 'c'], ['a', 'b', 'c'], ['b', 'c', 'd'], ['c', 'd', 'c'], ['d', 'c', 'd']]
By default, empty paths are not enumerated, but this can be parametrized:
sage: g.all_simple_paths(starting_vertices=['a'], trivial=True)
[['a'], ['a', 'a'], ['a', 'b'], ['a', 'b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b', 'c', 'd', 'c']]
sage: g.all_simple_paths(starting_vertices=['a'], trivial=False)
[['a', 'a'], ['a', 'b'], ['a', 'b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b', 'c', 'd', 'c']]
Returns the dig6 representation of the digraph as an ASCII string. Valid for single (no multiple edges) digraphs on 0 to 262143 vertices.
EXAMPLES:
sage: D = DiGraph()
sage: D.dig6_string()
'?'
sage: D.add_edge(0,1)
sage: D.dig6_string()
'AO'
Computes the minimum feedback edge set of a digraph (also called feedback arc set).
The minimum feedback edge set of a digraph is a set of edges
that intersect all the circuits of the digraph.
Equivalently, a minimum feedback arc set of a DiGraph is a set
 of arcs such that the digraph
of arcs such that the digraph 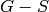 is acyclic. For more
information, see the
Wikipedia article on feedback arc sets.
is acyclic. For more
information, see the
Wikipedia article on feedback arc sets.
INPUT:
This problem is solved using Linear Programming, which certainly is not the best way and will have to be updated. The program to be solved is the following:
![\mbox{Minimize : }&\sum_{(u,v)\in G} b_{(u,v)}\\
\mbox{Such that : }&\\
&\forall v\in G, \sum_{i\in [0,\dots,n-1]}x_{v,i}=1\\
&\forall i\in [0,\dots,n-1], \sum_{v\in G}x_{v,i}=1\\
&\forall v\in G,\sum_{i\in [0,\dots,n-1]} ix_{v,i}=d_v\\
&\forall (u,v)\in G, d_u-d_v+nb_{(u,v)}\geq 0\\](../../_images/math/995c66bf775c2f49852c05e216b4e0dd9d844852.png)
An explanation:
An acyclic digraph can be seen as a poset, and every poset has
a linear extension. This means that in any acyclic digraph
the vertices can be ordered with a total order 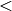 in such a way
that if
in such a way
that if 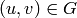 , then
, then 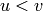 .
.
Thus, this linear program is built in order to assign to each vertex
 a unique number
a unique number ![d_v\in [0,\dots,n-1]](../../_images/math/dfc994bc5815fd6926037ed7ddf529c29ba58f97.png) such that if there exists
an edge
such that if there exists
an edge 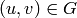 such that
such that 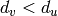 , then the edge
, then the edge 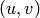 is
removed (
is
removed (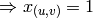 ).
).
The number of edges removed is then minimized, which is the objective.
EXAMPLES:
If the digraph is created from a graph, and hence is symmetric
(if 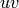 is an edge, then
is an edge, then 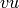 is an edge too), then
obviously the cardinality of its feedback arc set is the number
of edges in the first graph:
is an edge too), then
obviously the cardinality of its feedback arc set is the number
of edges in the first graph:
sage: cycle=graphs.CycleGraph(5)
sage: dcycle=DiGraph(cycle)
sage: cycle.size()
5
sage: dcycle.feedback_edge_set(value_only=True)
5.0
And in this situation, for any edge 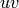 of the first graph,
of the first graph, 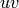 of
of 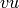 is in the returned feedback arc set:
is in the returned feedback arc set:
sage: g = graphs.RandomGNP(5,.3)
sage: dg = DiGraph(g)
sage: feedback = dg.feedback_edge_set()
sage: (u,v,l) = g.edge_iterator().next()
sage: (u,v) in feedback or (v,u) in feedback
True
Computes the minimum feedback vertex set of a digraph.
The minimum feedback vertex set of a digraph is a set of vertices
that intersect all the circuits of the digraph.
Equivalently, a minimum feedback vertex set of a DiGraph is a set
 of vertices such that the digraph
of vertices such that the digraph 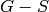 is acyclic. For more
information, see the
Wikipedia article on feedback vertex sets.
is acyclic. For more
information, see the
Wikipedia article on feedback vertex sets.
INPUT:
ALGORITHM:
This problem is solved using Linear Programming, which certainly is not the best way and will have to be replaced by a better algorithm. The program to be solved is the following:
![\mbox{Minimize : }&\sum_{v\in G} b_v\\
\mbox{Such that : }&\\
&\forall v\in G, \sum_{i\in [0,\dots,n-1]}x_{v,i}=1\\
&\forall i\in [0,\dots,n-1], \sum_{v\in G}x_{v,i}=1\\
&\forall v\in G,\sum_{i\in [0,\dots,n-1]} ix_{v,i}=d_v\\
&\forall (u,v)\in G, d_u-d_v+nb_u+nb_v\geq 0\\](../../_images/math/d43742f893e73f0bc1288495743903de22c49b53.png)
A brief explanation:
An acyclic digraph can be seen as a poset, and every poset has
a linear extension. This means that in any acyclic digraph
the vertices can be ordered with a total order 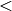 in such a way
that if
in such a way
that if 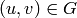 , then
, then 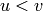 .
Thus, this linear program is built in order to assign to each vertex
.
Thus, this linear program is built in order to assign to each vertex
 an unique number
an unique number ![d_v\in [0,\dots,n-1]](../../_images/math/dfc994bc5815fd6926037ed7ddf529c29ba58f97.png) such that if there exists
an edge
such that if there exists
an edge 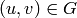 such that
such that 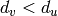 , then either
, then either 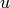 is removed
(
is removed
(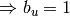 ) or
) or  is removed (
is removed (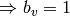 ).
The number of vertices removed is then minimized, which is
the objective.
).
The number of vertices removed is then minimized, which is
the objective.
EXAMPLES:
In a digraph built from a graph, any edge is replaced by arcs going in the two opposite directions, thus creating a cycle of length two. Hence, to remove all the cycles from the graph, each edge must see one of its neighbors removed : a feedback vertex set is in this situation a vertex cover:
sage: cycle=graphs.CycleGraph(5)
sage: dcycle=DiGraph(cycle)
sage: cycle.vertex_cover(value_only=True)
3
sage: feedback = dcycle.feedback_vertex_set()
sage: feedback.cardinality()
3
sage: (u,v,l) = cycle.edge_iterator().next()
sage: u in feedback or v in feedback
True
For a circuit, the minimum feedback arc set is clearly 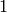 :
:
sage: circuit = digraphs.Circuit(5)
sage: circuit.feedback_vertex_set(value_only=True) == 1
True
Same as degree, but for in degree.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.in_degree(vertices = [0,1,2], labels=True)
{0: 2, 1: 2, 2: 2}
sage: D.in_degree()
[2, 2, 2, 2, 1, 1]
sage: G = graphs.PetersenGraph().to_directed()
sage: G.in_degree(0)
3
Same as degree_iterator, but for in degree.
EXAMPLES:
sage: D = graphs.Grid2dGraph(2,4).to_directed()
sage: for i in D.in_degree_iterator():
... print i
3
3
2
3
2
2
2
3
sage: for i in D.in_degree_iterator(labels=True):
... print i
((0, 1), 3)
((1, 2), 3)
((0, 0), 2)
((0, 2), 3)
((1, 3), 2)
((1, 0), 2)
((0, 3), 2)
((1, 1), 3)
Return the indegree sequence of this digraph.
EXAMPLES:
The indegree sequences of two digraphs:
sage: g = DiGraph({1: [2, 5, 6], 2: [3, 6], 3: [4, 6], 4: [6], 5: [4, 6]})
sage: g.in_degree_sequence()
[5, 2, 1, 1, 1, 0]
sage: V = [2, 3, 5, 7, 8, 9, 10, 11]
sage: E = [[], [8, 10], [11], [8, 11], [9], [], [], [2, 9, 10]]
sage: g = DiGraph(dict(zip(V, E)))
sage: g.in_degree_sequence()
[2, 2, 2, 2, 1, 0, 0, 0]
Return an iterator over all arriving edges from vertices, or over all edges if vertices is None.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: for a in D.incoming_edge_iterator([0]):
... print a
(1, 0, None)
(4, 0, None)
Returns a list of edges arriving at vertices.
INPUT:
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.incoming_edges([0])
[(1, 0, None), (4, 0, None)]
Since digraph is directed, returns True.
EXAMPLES:
sage: DiGraph().is_directed()
True
Returns whether the digraph is acyclic or not.
A directed graph is acyclic if for any vertex v, there is no directed path that starts and ends at v. Every directed acyclic graph (dag) corresponds to a partial ordering of its vertices, however multiple dags may lead to the same partial ordering.
EXAMPLES:
sage: D = DiGraph({ 0:[1,2,3], 4:[2,5], 1:[8], 2:[7], 3:[7], 5:[6,7], 7:[8], 6:[9], 8:[10], 9:[10] })
sage: D.plot(layout='circular').show()
sage: D.is_directed_acyclic()
True
sage: D.add_edge(9,7)
sage: D.is_directed_acyclic()
True
sage: D.add_edge(7,4)
sage: D.is_directed_acyclic()
False
Returns whether the current DiGraph is strongly connected.
EXAMPLE:
The circuit is obviously strongly connected
sage: g = digraphs.Circuit(5)
sage: g.is_strongly_connected()
True
But a transitive triangle is not:
sage: g = DiGraph({ 0 : [1,2], 1 : [2]})
sage: g.is_strongly_connected()
False
Computes a ranked layout so that all edges point upward. To this end, the heights of the vertices are set according to the level set decomposition of the graph (see level_sets()).
This is achieved by calling graphviz and dot2tex if available (see layout_acyclic_graphviz()), and using a random horizontal placement of the vertices otherwise (see layout_acyclic_dummy()).
Non acyclic graphs are partially supported by graphviz, which then chooses some edges to point down.
EXAMPLES:
sage: H = DiGraph({0:[1,2],1:[3],2:[3],3:[],5:[1,6],6:[2,3]})
sage: H.layout_acyclic()
{0: [..., ...], 1: [..., ...], 2: [..., ...], 3: [..., ...], 5: [..., ...], 6: [..., ...]}
Computes a (dummy) ranked layout of an acyclic graph so that all edges point upward. To this end, the heights of the vertices are set according to the level set decomposition of the graph (see level_sets()).
EXAMPLES:
sage: H = DiGraph({0:[1,2],1:[3],2:[3],3:[],5:[1,6],6:[2,3]})
sage: H.layout_acyclic_dummy()
{0: [..., 0], 1: [..., 1], 2: [..., 2], 3: [..., 3], 5: [..., 0], 6: [..., 1]}
sage: H = DiGraph({0:[1,2],1:[3],2:[3],3:[1],5:[1,6],6:[2,3]})
sage: H.layout_acyclic_dummy()
...
AssertionError: `self` should be an acyclic graph
OUTPUT:
- a list of non empty lists of vertices of this graph
Returns the level set decomposition of the graph. This a list
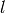 such that the level
such that the level ![l[i]](../../_images/math/8c08621a77c92ecbdc25becfa1e9aae7a26528b7.png) contains all the vertices
having all their predecessors in the levels
contains all the vertices
having all their predecessors in the levels ![l[j]](../../_images/math/14828b65a68c019fc048494713ec9ec64459956f.png) for
for 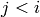 ,
and at least one in level
,
and at least one in level ![l[i-1]](../../_images/math/2bfc0ca1f7e52b1b5e83431b71e5d0a76386858a.png) (unless
(unless 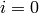 ).
).
The level decomposition contains exactly the vertices not occuring in any cycle of the graph. In particular, the graph is acyclic if and only if the decomposition forms a set partition of its vertices, and we recover the usual level set decomposition of the corresponding poset.
EXAMPLES:
sage: H = DiGraph({0:[1,2],1:[3],2:[3],3:[],5:[1,6],6:[2,3]})
sage: H.level_sets()
[[0, 5], [1, 6], [2], [3]]
sage: H = DiGraph({0:[1,2],1:[3],2:[3],3:[1],5:[1,6],6:[2,3]})
sage: H.level_sets()
[[0, 5], [6], [2]]
This routine is mostly used for Hasse diagrams of posets:
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2],1:[3],2:[3],3:[]})
sage: [len(x) for x in H.level_sets()]
[1, 2, 1]
sage: from sage.combinat.posets.hasse_diagram import HasseDiagram
sage: H = HasseDiagram({0:[1,2], 1:[3], 2:[4], 3:[4]})
sage: [len(x) for x in H.level_sets()]
[1, 2, 1, 1]
Complexity: 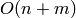 in time and
in time and 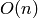 in memory (besides the
storage of the graph itself), where
in memory (besides the
storage of the graph itself), where  and
and 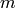 are
respectively the number of vertices and edges (assuming that
appending to a list is constant time, which it is not quite).
are
respectively the number of vertices and edges (assuming that
appending to a list is constant time, which it is not quite).
Returns an iterator over the in-neighbors of vertex.
An vertex 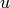 is an in-neighbor of a vertex
is an in-neighbor of a vertex  if
if 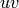 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: for a in D.neighbor_in_iterator(0):
... print a
1
4
Returns an iterator over the out-neighbors of a given vertex.
An vertex 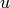 is an out-neighbor of a vertex
is an out-neighbor of a vertex  if
if 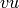 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: for a in D.neighbor_out_iterator(0):
... print a
1
2
3
Returns the list of the in-neighbors of a given vertex.
An vertex 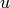 is an in-neighbor of a vertex
is an in-neighbor of a vertex  if
if 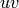 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.neighbors_in(0)
[1, 4]
Returns the list of the out-neighbors of a given vertex.
An vertex 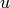 is an out-neighbor of a vertex
is an out-neighbor of a vertex  if
if 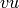 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.neighbors_out(0)
[1, 2, 3]
Same as degree, but for out degree.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.out_degree(vertices = [0,1,2], labels=True)
{0: 3, 1: 2, 2: 1}
sage: D.out_degree()
[3, 2, 1, 1, 2, 1]
Same as degree_iterator, but for out degree.
EXAMPLES:
sage: D = graphs.Grid2dGraph(2,4).to_directed()
sage: for i in D.out_degree_iterator():
... print i
3
3
2
3
2
2
2
3
sage: for i in D.out_degree_iterator(labels=True):
... print i
((0, 1), 3)
((1, 2), 3)
((0, 0), 2)
((0, 2), 3)
((1, 3), 2)
((1, 0), 2)
((0, 3), 2)
((1, 1), 3)
Return the outdegree sequence of this digraph.
EXAMPLES:
The outdegree sequences of two digraphs:
sage: g = DiGraph({1: [2, 5, 6], 2: [3, 6], 3: [4, 6], 4: [6], 5: [4, 6]})
sage: g.out_degree_sequence()
[3, 2, 2, 2, 1, 0]
sage: V = [2, 3, 5, 7, 8, 9, 10, 11]
sage: E = [[], [8, 10], [11], [8, 11], [9], [], [], [2, 9, 10]]
sage: g = DiGraph(dict(zip(V, E)))
sage: g.out_degree_sequence()
[3, 2, 2, 1, 1, 0, 0, 0]
Return an iterator over all departing edges from vertices, or over all edges if vertices is None.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: for a in D.outgoing_edge_iterator([0]):
... print a
(0, 1, None)
(0, 2, None)
(0, 3, None)
Returns a list of edges departing from vertices.
INPUT:
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.outgoing_edges([0])
[(0, 1, None), (0, 2, None), (0, 3, None)]
Returns an iterator over the in-neighbors of vertex.
An vertex 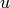 is an in-neighbor of a vertex
is an in-neighbor of a vertex  if
if 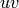 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: for a in D.neighbor_in_iterator(0):
... print a
1
4
Returns the list of the in-neighbors of a given vertex.
An vertex 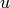 is an in-neighbor of a vertex
is an in-neighbor of a vertex  if
if 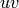 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.neighbors_in(0)
[1, 4]
Returns a copy of digraph with edges reversed in direction.
EXAMPLES:
sage: D = DiGraph({ 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] })
sage: D.reverse()
Reverse of (): Digraph on 6 vertices
Returns the set of vertices whose strongly connected component is the same as v’s.
INPUT:
EXAMPLE:
In the symmetric digraph of a graph, the strongly connected components are the connected components:
sage: g = graphs.PetersenGraph()
sage: d = DiGraph(g)
sage: d.strongly_connected_component_containing_vertex(0)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Returns a list of lists of vertices, each list representing a strongly connected component.
EXAMPLES:
sage: D = DiGraph( { 0 : [1, 3], 1 : [2], 2 : [3], 4 : [5, 6], 5 : [6] } )
sage: D.connected_components()
[[0, 1, 2, 3], [4, 5, 6]]
sage: D = DiGraph( { 0 : [1, 3], 1 : [2], 2 : [3], 4 : [5, 6], 5 : [6] } )
sage: D.strongly_connected_components()
[[0], [1], [2], [3], [4], [5], [6]]
sage: D.add_edge([2,0])
sage: D.strongly_connected_components()
[[0, 1, 2], [3], [4], [5], [6]]
Returns the digraph of the strongly connected components
The digraph of the strongly connected components of a graph  has
a vertex per strongly connected component included in
has
a vertex per strongly connected component included in  . There
is an edge from a component
. There
is an edge from a component 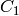 to a component
to a component 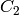 if there is
an edge from one to the other in
if there is
an edge from one to the other in  .
.
EXAMPLE:
Such a digraph is always acyclic
sage: g = digraphs.RandomDirectedGNP(15,.1)
sage: scc_digraph = g.strongly_connected_components_digraph()
sage: scc_digraph.is_directed_acyclic()
True
The vertices of the digraph of strongly connected components are exactly the strongly connected components:
sage: g = digraphs.ButterflyGraph(2)
sage: scc_digraph = g.strongly_connected_components_digraph()
sage: g.is_directed_acyclic()
True
sage: all([ Set(scc) in scc_digraph.vertices() for scc in g.strongly_connected_components()])
True
Returns the strongly connected components as a list of subgraphs.
EXAMPLE:
In the symmetric digraph of a graph, the strongly connected components are the connected components:
sage: g = graphs.PetersenGraph()
sage: d = DiGraph(g)
sage: d.strongly_connected_components_subgraphs()
[Subgraph of (Petersen graph): Digraph on 10 vertices]
Returns an iterator over the out-neighbors of a given vertex.
An vertex 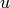 is an out-neighbor of a vertex
is an out-neighbor of a vertex  if
if 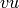 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: for a in D.neighbor_out_iterator(0):
... print a
1
2
3
Returns the list of the out-neighbors of a given vertex.
An vertex 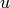 is an out-neighbor of a vertex
is an out-neighbor of a vertex  if
if 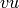 in an edge.
in an edge.
EXAMPLES:
sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } )
sage: D.neighbors_out(0)
[1, 2, 3]
Since the graph is already directed, simply returns a copy of itself.
EXAMPLES:
sage: DiGraph({0:[1,2,3],4:[5,1]}).to_directed()
Digraph on 6 vertices
Returns an undirected version of the graph. Every directed edge becomes an edge.
EXAMPLES:
sage: D = DiGraph({0:[1,2],1:[0]})
sage: G = D.to_undirected()
sage: D.edges(labels=False)
[(0, 1), (0, 2), (1, 0)]
sage: G.edges(labels=False)
[(0, 1), (0, 2)]
Returns a topological sort of the digraph if it is acyclic, and raises a TypeError if the digraph contains a directed cycle.
A topological sort is an ordering of the vertices of the digraph such that each vertex comes before all of its successors. That is, if u comes before v in the sort, then there may be a directed path from u to v, but there will be no directed path from v to u.
EXAMPLES:
sage: D = DiGraph({ 0:[1,2,3], 4:[2,5], 1:[8], 2:[7], 3:[7], 5:[6,7], 7:[8], 6:[9], 8:[10], 9:[10] })
sage: D.plot(layout='circular').show()
sage: D.topological_sort()
[4, 5, 6, 9, 0, 1, 2, 3, 7, 8, 10]
sage: D.add_edge(9,7)
sage: D.topological_sort()
[4, 5, 6, 9, 0, 1, 2, 3, 7, 8, 10]
sage: D.add_edge(7,4)
sage: D.topological_sort()
...
TypeError: Digraph is not acyclic-- there is no topological sort.
Note
There is a recursive version of this in NetworkX, but it has problems:
sage: import networkx
sage: D = DiGraph({ 0:[1,2,3], 4:[2,5], 1:[8], 2:[7], 3:[7], 5:[6,7], 7:[8], 6:[9], 8:[10], 9:[10] })
sage: N = D.networkx_graph()
sage: networkx.topological_sort(N)
[4, 5, 6, 9, 0, 1, 2, 3, 7, 8, 10]
sage: networkx.topological_sort_recursive(N) is None
True
Returns a list of all topological sorts of the digraph if it is acyclic, and raises a TypeError if the digraph contains a directed cycle.
A topological sort is an ordering of the vertices of the digraph such that each vertex comes before all of its successors. That is, if u comes before v in the sort, then there may be a directed path from u to v, but there will be no directed path from v to u. See also Graph.topological_sort().
AUTHORS:
REFERENCE:
EXAMPLES:
sage: D = DiGraph({ 0:[1,2], 1:[3], 2:[3,4] })
sage: D.plot(layout='circular').show()
sage: D.topological_sort_generator()
[[0, 1, 2, 3, 4], [0, 1, 2, 4, 3], [0, 2, 1, 3, 4], [0, 2, 1, 4, 3], [0, 2, 4, 1, 3]]
sage: for sort in D.topological_sort_generator():
... for edge in D.edge_iterator():
... u,v,l = edge
... if sort.index(u) > sort.index(v):
... print "This should never happen."