Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Cryptography »

Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Linear feedback shift register cryptosystem class
Bases: sage.crypto.cryptosystem.SymmetricKeyCryptosystem
Shrinking generator cryptosystem class
The Blum-Blum-Shub (BBS) pseudorandom bit generator.
See the original paper by Blum, Blum and Shub [BlumBlumShub1986]. The BBS algorithm is also discussed in section 5.5.2 of [MenezesEtAl1996].
INPUT:
 and
and  are Blum primes, then
seed is a quadratic residue in the multiplicative group
are Blum primes, then
seed is a quadratic residue in the multiplicative group
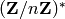 where
where 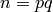 . If seed=None, then the function
would generate its own random quadratic residue in
. If seed=None, then the function
would generate its own random quadratic residue in 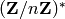 .
If you provide a value for seed, then it is your responsibility to
ensure that the seed is a quadratic residue in the multiplicative group
.
If you provide a value for seed, then it is your responsibility to
ensure that the seed is a quadratic residue in the multiplicative group
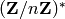 .
. and
and  can be. So we
have 0 < lbound <= p, q <= ubound. The lower bound must be
distinct from the upper bound.
can be. So we
have 0 < lbound <= p, q <= ubound. The lower bound must be
distinct from the upper bound. and
and  can be. So we have
0 < lbound <= p, q <= ubound. The lower bound must be distinct
from the upper bound.
can be. So we have
0 < lbound <= p, q <= ubound. The lower bound must be distinct
from the upper bound.OUTPUT:
Here is a common use case for this function. If you want this
function to use pre-computed values for  and
and  , you should pass
those pre-computed values to this function. In that case, you only need
to specify values for length, p and q, and you do not need
to worry about doing anything with the parameters lbound and
ubound. The pre-computed values
, you should pass
those pre-computed values to this function. In that case, you only need
to specify values for length, p and q, and you do not need
to worry about doing anything with the parameters lbound and
ubound. The pre-computed values  and
and  must be Blum primes.
It is your responsibility to check that both
must be Blum primes.
It is your responsibility to check that both  and
and  are Blum primes.
are Blum primes.
Here is another common use case. If you want the function to generate
its own values for  and
and  , you must specify the lower and upper
bounds within which these two primes must lie. In that case, you must
specify values for length, lbound and ubound, and you do
not need to worry about values for the parameters p and q. The
parameter ntries is only relevant when you want this function to
generate p and q.
, you must specify the lower and upper
bounds within which these two primes must lie. In that case, you must
specify values for length, lbound and ubound, and you do
not need to worry about values for the parameters p and q. The
parameter ntries is only relevant when you want this function to
generate p and q.
Note
Beware that there might not be any primes between the lower and upper bounds. So make sure that these two bounds are “sufficiently” far apart from each other for there to be primes congruent to 3 modulo 4. In particular, there should be at least two distinct primes within these bounds, each prime being congruent to 3 modulo 4. This function uses the function random_blum_prime() to generate random primes that are congruent to 3 modulo 4.
ALGORITHM:
The BBS algorithm as described below is adapted from the presentation in Algorithm 5.40, page 186 of [MenezesEtAl1996].
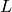 be the desired number of bits in the output bit sequence.
That is,
be the desired number of bits in the output bit sequence.
That is, 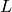 is the desired length of the bit string.
is the desired length of the bit string. and
and  be two large distinct primes, each congruent to 3
modulo 4.
be two large distinct primes, each congruent to 3
modulo 4.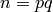 be the product of
be the product of  and
and  .
.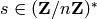 , where
, where
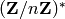 is the multiplicative group of
is the multiplicative group of 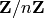 .
.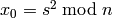 .
. from 1 to
from 1 to 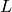 , do
, do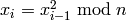 .
.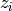 be the least significant bit of
be the least significant bit of 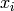 .
.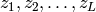 .
.EXAMPLES:
A BBS pseudorandom bit sequence with a specified seed:
sage: from sage.crypto.stream import blum_blum_shub
sage: blum_blum_shub(length=6, seed=3, p=11, q=19)
110000
You could specify the length of the bit string, with given values for p and q:
sage: blum_blum_shub(length=6, p=11, q=19) # random
001011
Or you could specify the length of the bit string, with given values for the lower and upper bounds:
sage: blum_blum_shub(length=6, lbound=10**4, ubound=10**5) # random
110111
Under some reasonable hypotheses, Blum-Blum-Shub [BlumBlumShub1982]
sketch a proof that the period of the BBS stream cipher is equal to
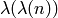 , where
, where 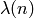 is the Carmichael function of
is the Carmichael function of
 . This is verified below in a few examples by using the function
lfsr_connection_polynomial()
(written by Tim Brock) which computes the connection polynomial of a
linear feedback shift register sequence. The degree of that polynomial
is the period.
. This is verified below in a few examples by using the function
lfsr_connection_polynomial()
(written by Tim Brock) which computes the connection polynomial of a
linear feedback shift register sequence. The degree of that polynomial
is the period.
sage: from sage.crypto.stream import blum_blum_shub
sage: from sage.crypto.util import carmichael_lambda
sage: carmichael_lambda(carmichael_lambda(7*11))
4
sage: s = [GF(2)(int(str(x))) for x in blum_blum_shub(60, p=7, q=11, seed=13)]
sage: lfsr_connection_polynomial(s)
x^3 + x^2 + x + 1
sage: carmichael_lambda(carmichael_lambda(11*23))
20
sage: s = [GF(2)(int(str(x))) for x in blum_blum_shub(60, p=11, q=23, seed=13)]
sage: lfsr_connection_polynomial(s)
x^19 + x^18 + x^17 + x^16 + x^15 + x^14 + x^13 + x^12 + x^11 + x^10 + x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1
TESTS:
Make sure that there is at least one Blum prime between the lower and upper bounds. In the following example, we have lbound=24 and ubound=30 with 29 being the only prime within those bounds. But 29 is not a Blum prime.
sage: from sage.crypto.stream import blum_blum_shub
sage: blum_blum_shub(6, lbound=24, ubound=30, ntries=10)
...
ValueError: No Blum primes within the specified closed interval.
Both the lower and upper bounds must be greater than 2:
sage: blum_blum_shub(6, lbound=2, ubound=3)
...
ValueError: Both the lower and upper bounds must be > 2.
sage: blum_blum_shub(6, lbound=3, ubound=2)
...
ValueError: Both the lower and upper bounds must be > 2.
sage: blum_blum_shub(6, lbound=2, ubound=2)
...
ValueError: Both the lower and upper bounds must be > 2.
The lower and upper bounds must be distinct from each other:
sage: blum_blum_shub(6, lbound=3, ubound=3)
...
ValueError: The lower and upper bounds must be distinct.
The lower bound must be less than the upper bound:
sage: blum_blum_shub(6, lbound=4, ubound=3)
...
ValueError: The lower bound must be less than the upper bound.
REFERENCES:
| [BlumBlumShub1982] | L. Blum, M. Blum, and M. Shub. Comparison of Two Pseudo-Random Number Generators. Advances in Cryptology: Proceedings of Crypto ‘82, pp.61–78, 1982. |
| [BlumBlumShub1986] | L. Blum, M. Blum, and M. Shub. A Simple Unpredictable Pseudo-Random Number Generator. SIAM Journal on Computing, 15(2):364–383, 1986. |