Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Cryptography »

Miscellaneous utility functions for cryptographic purposes.
AUTHORS:
Return the ASCII integer corresponding to the binary string B.
INPUT:
OUTPUT:
EXAMPLES:
The ASCII integers of some binary strings:
sage: from sage.crypto.util import ascii_integer
sage: bin = BinaryStrings()
sage: B = bin.encoding("A"); B
01000001
sage: ascii_integer(B)
65
sage: B = bin.encoding("C"); list(B)
[0, 1, 0, 0, 0, 0, 1, 1]
sage: ascii_integer(list(B))
67
sage: ascii_integer("01000100")
68
sage: ascii_integer([0, 1, 0, 0, 0, 1, 0, 1])
69
TESTS:
The input B must be a non-empty string or a non-empty list of bits:
sage: from sage.crypto.util import ascii_integer
sage: ascii_integer("")
...
ValueError: B must consist of 8 bits.
sage: ascii_integer([])
...
ValueError: B must consist of 8 bits.
The input B must be an 8-bit string or a list of 8 bits:
sage: from sage.crypto.util import ascii_integer
sage: ascii_integer("101")
...
ValueError: B must consist of 8 bits.
sage: ascii_integer([1, 0, 1, 1])
...
ValueError: B must consist of 8 bits.
Return the binary representation of the ASCII string A.
INPUT:
OUTPUT:
ALGORITHM:
Let 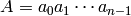 be an ASCII string, where each
be an ASCII string, where each 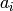 is
an ASCII character. Let
is
an ASCII character. Let 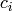 be the ASCII integer corresponding to
be the ASCII integer corresponding to 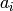 and let
and let 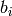 be the binary representation of
be the binary representation of 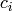 . The binary
representation
. The binary
representation  of
of  is
is 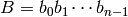 .
.
EXAMPLES:
The binary representation of some ASCII strings:
sage: from sage.crypto.util import ascii_to_bin
sage: ascii_to_bin("A")
01000001
sage: ascii_to_bin("Abc123")
010000010110001001100011001100010011001000110011
The empty string is different from the string with one space character. For the empty string and the empty list, this function returns the same result:
sage: from sage.crypto.util import ascii_to_bin
sage: ascii_to_bin("")
<BLANKLINE>
sage: ascii_to_bin(" ")
00100000
sage: ascii_to_bin([])
<BLANKLINE>
This function also accepts a list of ASCII characters. You can also pass in a list of strings:
sage: from sage.crypto.util import ascii_to_bin
sage: ascii_to_bin(["A", "b", "c", "1", "2", "3"])
010000010110001001100011001100010011001000110011
sage: ascii_to_bin(["A", "bc", "1", "23"])
010000010110001001100011001100010011001000110011
TESTS:
For a list of ASCII characters or strings, do not mix characters or strings with integers:
sage: from sage.crypto.util import ascii_to_bin
sage: ascii_to_bin(["A", "b", "c", 1, 2, 3])
...
TypeError: sequence item 3: expected string, sage.rings.integer.Integer found
sage: ascii_to_bin(["Abc", 1, 2, 3])
...
TypeError: sequence item 1: expected string, sage.rings.integer.Integer found
Return the ASCII representation of the binary string B.
INPUT:
OUTPUT:
ALGORITHM:
Consider a block of bits 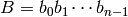 where each
sub-block
where each
sub-block 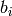 is a binary string of length 8. Then the total number
of bits is a multiple of 8 and is given by
is a binary string of length 8. Then the total number
of bits is a multiple of 8 and is given by 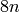 . Let
. Let 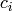 be the
integer representation of
be the
integer representation of 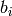 . We can consider
. We can consider 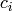 as the integer
representation of an ASCII character. Then the ASCII representation
as the integer
representation of an ASCII character. Then the ASCII representation
 of
of  is
is 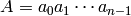 .
.
EXAMPLES:
Convert some ASCII strings to their binary representations and recover the ASCII strings from the binary representations:
sage: from sage.crypto.util import ascii_to_bin
sage: from sage.crypto.util import bin_to_ascii
sage: A = "Abc"
sage: B = ascii_to_bin(A); B
010000010110001001100011
sage: bin_to_ascii(B)
'Abc'
sage: bin_to_ascii(B) == A
True
sage: A = "123 \" #"
sage: B = ascii_to_bin(A); B
00110001001100100011001100100000001000100010000000100011
sage: bin_to_ascii(B)
'123 " #'
sage: bin_to_ascii(B) == A
True
This function also accepts strings and lists of bits:
sage: from sage.crypto.util import bin_to_ascii
sage: bin_to_ascii("010000010110001001100011")
'Abc'
sage: bin_to_ascii([0, 1, 0, 0, 0, 0, 0, 1])
'A'
TESTS:
The number of bits in B must be non-empty and a multiple of 8:
sage: from sage.crypto.util import bin_to_ascii
sage: bin_to_ascii("")
...
ValueError: B must be a non-empty binary string.
sage: bin_to_ascii([])
...
ValueError: B must be a non-empty binary string.
sage: bin_to_ascii(" ")
...
ValueError: The number of bits in B must be a multiple of 8.
sage: bin_to_ascii("101")
...
ValueError: The number of bits in B must be a multiple of 8.
sage: bin_to_ascii([1, 0, 1])
...
ValueError: The number of bits in B must be a multiple of 8.
Return the Carmichael function of a positive integer n.
The Carmichael function of  , denoted
, denoted 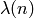 , is the smallest
positive integer
, is the smallest
positive integer  such that
such that 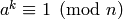 for all
for all
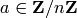 satisfying
satisfying 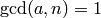 . Thus,
. Thus, 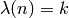 is the exponent of the multiplicative group
is the exponent of the multiplicative group 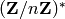 .
.
INPUT:
OUTPUT:
ALGORITHM:
If 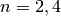 then
then 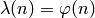 . Let
. Let 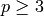 be an odd
prime and let
be an odd
prime and let  be a positive integer. Then
be a positive integer. Then
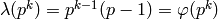 . If
. If 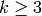 , then
, then
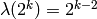 . Now consider the case where
. Now consider the case where 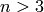 is
composite and let
is
composite and let 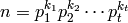 be the
prime factorization of
be the
prime factorization of  . Then
. Then
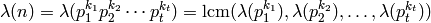
EXAMPLES:
The Carmichael function of all positive integers up to and including 10:
sage: from sage.crypto.util import carmichael_lambda
sage: map(carmichael_lambda, [1..10])
[1, 1, 2, 2, 4, 2, 6, 2, 6, 4]
The Carmichael function of the first ten primes:
sage: map(carmichael_lambda, primes_first_n(10))
[1, 2, 4, 6, 10, 12, 16, 18, 22, 28]
Cases where the Carmichael function is equivalent to the Euler phi function:
sage: carmichael_lambda(2) == euler_phi(2)
True
sage: carmichael_lambda(4) == euler_phi(4)
True
sage: p = random_prime(1000, lbound=3, proof=True)
sage: k = randint(1, 1000)
sage: carmichael_lambda(p^k) == euler_phi(p^k)
True
A case where 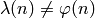 :
:
sage: k = randint(1, 1000)
sage: carmichael_lambda(2^k) == 2^(k - 2)
True
sage: carmichael_lambda(2^k) == 2^(k - 2) == euler_phi(2^k)
False
Verifying the current implementation of the Carmichael function using
another implemenation. The other implementation that we use for
verification is an exhaustive search for the exponent of the
multiplicative group 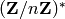 .
.
sage: from sage.crypto.util import carmichael_lambda
sage: n = randint(1, 500)
sage: c = carmichael_lambda(n)
sage: def coprime(n):
... return [i for i in xrange(n) if gcd(i, n) == 1]
...
sage: def znpower(n, k):
... L = coprime(n)
... return map(power_mod, L, [k]*len(L), [n]*len(L))
...
sage: def my_carmichael(n):
... for k in xrange(1, n):
... L = znpower(n, k)
... ones = [1] * len(L)
... T = [L[i] == ones[i] for i in xrange(len(L))]
... if all(T):
... return k
...
sage: c == my_carmichael(n)
True
Carmichael’s theorem states that 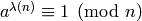 for all elements
for all elements  of the multiplicative group
of the multiplicative group 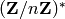 .
Here, we verify Carmichael’s theorem.
.
Here, we verify Carmichael’s theorem.
sage: from sage.crypto.util import carmichael_lambda
sage: n = randint(1, 1000)
sage: c = carmichael_lambda(n)
sage: ZnZ = IntegerModRing(n)
sage: M = ZnZ.list_of_elements_of_multiplicative_group()
sage: ones = [1] * len(M)
sage: P = [power_mod(a, c, n) for a in M]
sage: P == ones
True
TESTS:
The input n must be a positive integer:
sage: from sage.crypto.util import carmichael_lambda
sage: carmichael_lambda(0)
...
ValueError: Input n must be a positive integer.
sage: carmichael_lambda(randint(-10, 0))
...
ValueError: Input n must be a positive integer.
Bug reported in trac #8283:
sage: from sage.crypto.util import carmichael_lambda
sage: type(carmichael_lambda(16))
<type 'sage.rings.integer.Integer'>
REFERENCES:
| [Carmichael2010] | Carmichael function, http://en.wikipedia.org/wiki/Carmichael_function |
Determine whether or not there is a Blum prime within the specified closed interval.
INPUT:
OUTPUT:
ALGORITHM:
Let  and
and 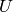 be distinct positive integers. Let
be distinct positive integers. Let  be the set of all
odd primes
be the set of all
odd primes  such that
such that 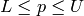 . Our main focus is on Blum
primes, i.e. odd primes that are congruent to 3 modulo 4, so we assume
that the lower bound
. Our main focus is on Blum
primes, i.e. odd primes that are congruent to 3 modulo 4, so we assume
that the lower bound 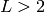 . The closed interval
. The closed interval ![[L, U]](../../_images/math/ff7d09c3fd7e7b2fa52079404b6c254d1f9cdf00.png) has a Blum
prime if and only if the set
has a Blum
prime if and only if the set  has a Blum prime.
has a Blum prime.
EXAMPLES:
Testing for the presence of Blum primes within some closed intervals.
The interval ![[4, 100]](../../_images/math/4934c5f26a19cfabb0409a8b6b9318925f0df2e6.png) has a Blum prime, the smallest such prime being
7. The interval
has a Blum prime, the smallest such prime being
7. The interval ![[24, 28]](../../_images/math/97abdb43e914727c929aaae6454541471dc1fbe6.png) has no primes, hence no Blum primes.
has no primes, hence no Blum primes.
sage: from sage.crypto.util import has_blum_prime
sage: from sage.crypto.util import is_blum_prime
sage: has_blum_prime(4, 100)
True
sage: for n in xrange(4, 100):
... if is_blum_prime(n):
... print n
... break
...
7
sage: has_blum_prime(24, 28)
False
TESTS:
Both the lower and upper bounds must be greater than 2:
sage: from sage.crypto.util import has_blum_prime
sage: has_blum_prime(2, 3)
...
ValueError: Both the lower and upper bounds must be > 2.
sage: has_blum_prime(3, 2)
...
ValueError: Both the lower and upper bounds must be > 2.
sage: has_blum_prime(2, 2)
...
ValueError: Both the lower and upper bounds must be > 2.
The lower and upper bounds must be distinct from each other:
sage: has_blum_prime(3, 3)
...
ValueError: The lower and upper bounds must be distinct.
The lower bound must be less than the upper bound:
sage: has_blum_prime(4, 3)
...
ValueError: The lower bound must be less than the upper bound.
Determine whether or not n is a Blum prime.
INPUT:
OUTPUT:
Let  be a positive prime. Then
be a positive prime. Then  is a Blum prime if
is a Blum prime if  is
congruent to 3 modulo 4, i.e.
is
congruent to 3 modulo 4, i.e. 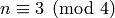 .
.
EXAMPLES:
Testing some integers to see if they are Blum primes:
sage: from sage.crypto.util import is_blum_prime
sage: from sage.crypto.util import random_blum_prime
sage: is_blum_prime(101)
False
sage: is_blum_prime(7)
True
sage: p = random_blum_prime(10**3, 10**5)
sage: is_blum_prime(p)
True
Return the k least significant bits of n.
INPUT:
OUTPUT:
 be the
binary representation of n, where
be the
binary representation of n, where  is the length of the
binary string
is the length of the
binary string  . If
. If 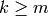 , then return the binary
representation of n.
, then return the binary
representation of n.EXAMPLES:
Obtain the parity bits of some integers:
sage: from sage.crypto.util import least_significant_bits
sage: least_significant_bits(0, 1)
[0]
sage: least_significant_bits(2, 1)
[0]
sage: least_significant_bits(3, 1)
[1]
sage: least_significant_bits(-2, 1)
[0]
sage: least_significant_bits(-3, 1)
[1]
Obtain the 4 least significant bits of some integers:
sage: least_significant_bits(101, 4)
[0, 1, 0, 1]
sage: least_significant_bits(-101, 4)
[0, 1, 0, 1]
sage: least_significant_bits(124, 4)
[1, 1, 0, 0]
sage: least_significant_bits(-124, 4)
[1, 1, 0, 0]
The binary representation of 123:
sage: n = 123; b = n.binary(); b
'1111011'
sage: least_significant_bits(n, len(b))
[1, 1, 1, 1, 0, 1, 1]
A random Blum prime within the specified bounds.
Let  be a positive prime. Then
be a positive prime. Then  is a Blum prime if
is a Blum prime if  is
congruent to 3 modulo 4, i.e.
is
congruent to 3 modulo 4, i.e. 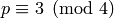 .
.
INPUT:
 can be. So we have
0 < lbound <= p <= ubound. The lower bound must be distinct from
the upper bound.
can be. So we have
0 < lbound <= p <= ubound. The lower bound must be distinct from
the upper bound. can be. So we have
0 < lbound <= p <= ubound. The lower bound must be distinct
from the upper bound.
can be. So we have
0 < lbound <= p <= ubound. The lower bound must be distinct
from the upper bound.OUTPUT:
Note
Beware that there might not be any primes between the lower and upper bounds. So make sure that these two bounds are “sufficiently” far apart from each other for there to be primes congruent to 3 modulo 4. In particular, there should be at least two distinct Blum primes within the specified bounds.
EXAMPLES:
Choose a random prime and check that it is a Blum prime:
sage: from sage.crypto.util import random_blum_prime
sage: p = random_blum_prime(10**4, 10**5)
sage: is_prime(p)
True
sage: mod(p, 4) == 3
True
TESTS:
Make sure that there is at least one Blum prime between the lower and upper bounds. In the following example, we have lbound=24 and ubound=30 with 29 being the only prime within those bounds. But 29 is not a Blum prime.
sage: from sage.crypto.util import random_blum_prime
sage: random_blum_prime(24, 30, ntries=10)
...
ValueError: No Blum primes within the specified closed interval.
sage: random_blum_prime(24, 28)
...
ValueError: No Blum primes within the specified closed interval.