Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Cryptography »

The Blum-Goldwasser probabilistic public-key encryption scheme. This scheme was originally described in [BlumGoldwasser1985]. See also section 8.7.2 of [MenezesEtAl1996] and the Wikipedia article on this scheme.
REFERENCES:
| [BlumGoldwasser1985] | M. Blum and S. Goldwasser. An Efficient Probabilistic Public-Key Encryption Scheme Which Hides All Partial Information. In Proceedings of CRYPTO 84 on Advances in Cryptology, pp. 289–299, Springer, 1985. |
| [MenezesEtAl1996] | (1, 2, 3, 4, 5, 6, 7, 8) A. J. Menezes, P. C. van Oorschot, and S. A. Vanstone. Handbook of Applied Cryptography. CRC Press, 1996. |
AUTHORS:
Bases: sage.crypto.cryptosystem.PublicKeyCryptosystem
The Blum-Goldwasser probabilistic public-key encryption scheme.
The Blum-Goldwasser encryption and decryption algorithms as described in
encrypt() and
decrypt(), respectively, make use of the
least significant bit of a binary string. A related concept is the  least significant bits of a binary string. For example, given a positive
integer
least significant bits of a binary string. For example, given a positive
integer  , let
, let 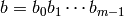 be the binary representation
of
be the binary representation
of  so that
so that  is a binary string of length
is a binary string of length  . Then the least
significant bit of
. Then the least
significant bit of  is
is 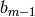 . If
. If 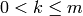 , then the
, then the  least
significant bits of
least
significant bits of  are
are 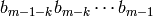 . The least
significant bit of an integer is also referred to as its parity bit,
because this bit determines whether the integer is even or odd. In the
following example, we obtain the least significant bit of an integer:
. The least
significant bit of an integer is also referred to as its parity bit,
because this bit determines whether the integer is even or odd. In the
following example, we obtain the least significant bit of an integer:
sage: n = 123
sage: b = n.binary(); b
'1111011'
sage: n % 2
1
sage: b[-1]
'1'
Now find the 4 least significant bits of the integer 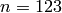 :
:
sage: b
'1111011'
sage: b[-4:]
'1011'
The last two examples could be worked through as follows:
sage: from sage.crypto.util import least_significant_bits
sage: least_significant_bits(123, 1)
[1]
sage: least_significant_bits(123, 4)
[1, 0, 1, 1]
EXAMPLES:
The following encryption/decryption example is taken from Example 8.57, pages 309–310 of [MenezesEtAl1996]:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser(); bg
The Blum-Goldwasser public-key encryption scheme.
sage: p = 499; q = 547
sage: pubkey = bg.public_key(p, q); pubkey
272953
sage: prikey = bg.private_key(p, q); prikey
(499, 547, -57, 52)
sage: P = "10011100000100001100"
sage: C = bg.encrypt(P, pubkey, seed=159201); C
([[0, 0, 1, 0], [0, 0, 0, 0], [1, 1, 0, 0], [1, 1, 1, 0], [0, 1, 0, 0]], 139680)
sage: M = bg.decrypt(C, prikey); M
[[1, 0, 0, 1], [1, 1, 0, 0], [0, 0, 0, 1], [0, 0, 0, 0], [1, 1, 0, 0]]
sage: M = "".join(map(lambda x: str(x), flatten(M))); M
'10011100000100001100'
sage: M == P
True
Generate a pair of random public/private keys. Use the public key to encrypt a plaintext. Then decrypt the resulting ciphertext using the private key. Finally, compare the decrypted message with the original plaintext.
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: from sage.crypto.util import bin_to_ascii
sage: bg = BlumGoldwasser()
sage: pubkey, prikey = bg.random_key(10**4, 10**6)
sage: P = "A fixed plaintext."
sage: C = bg.encrypt(P, pubkey)
sage: M = bg.decrypt(C, prikey)
sage: bin_to_ascii(flatten(M)) == P
True
If 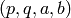 is a private key, then
is a private key, then 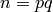 is the corresponding
public key. Furthermore, we have
is the corresponding
public key. Furthermore, we have 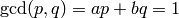 .
.
sage: p, q, a, b = prikey
sage: pubkey == p * q
True
sage: gcd(p, q) == a*p + b*q == 1
True
Apply the Blum-Goldwasser scheme to decrypt the ciphertext C using the private key K.
INPUT:
 must
be of the form
must
be of the form 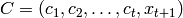 . Each
. Each 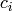 is a sub-block of binary string and
is a sub-block of binary string and 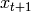 is the result of the
is the result of the
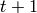 -th iteration of the Blum-Blum-Shub algorithm.
-th iteration of the Blum-Blum-Shub algorithm.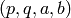 where
where  and
and  are
distinct Blum primes and
are
distinct Blum primes and 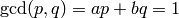 .
.OUTPUT:
ALGORITHM:
The Blum-Goldwasser decryption algorithm is described in Algorithm 8.56, page 309 of [MenezesEtAl1996]. The algorithm works as follows:
 be the ciphertext
be the ciphertext 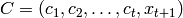 .
Then
.
Then  is the number of ciphertext sub-blocks and
is the number of ciphertext sub-blocks and 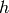 is the
length of each binary string sub-block
is the
length of each binary string sub-block 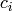 .
.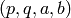 be the private key whose corresponding
public key is
be the private key whose corresponding
public key is 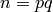 . Note that
. Note that 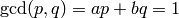 .
.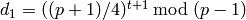 .
.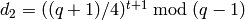 .
.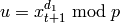 .
.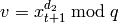 .
.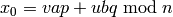 .
. from 1 to
from 1 to  , do:
, do: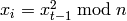 .
.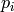 be the
be the 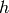 least significant bits of
least significant bits of 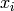 .
.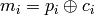 .
.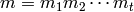 .
.EXAMPLES:
The following decryption example is taken from Example 8.57, pages 309–310 of [MenezesEtAl1996]. Here we decrypt a binary string:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: p = 499; q = 547
sage: C = ([[0, 0, 1, 0], [0, 0, 0, 0], [1, 1, 0, 0], [1, 1, 1, 0], [0, 1, 0, 0]], 139680)
sage: K = bg.private_key(p, q); K
(499, 547, -57, 52)
sage: P = bg.decrypt(C, K); P
[[1, 0, 0, 1], [1, 1, 0, 0], [0, 0, 0, 1], [0, 0, 0, 0], [1, 1, 0, 0]]
Convert the plaintext sub-blocks into a binary string:
sage: bin = BinaryStrings()
sage: bin(flatten(P))
10011100000100001100
Decrypt a longer ciphertext and convert the resulting plaintext into an ASCII string:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: from sage.crypto.util import bin_to_ascii
sage: bg = BlumGoldwasser()
sage: p = 78307; q = 412487
sage: K = bg.private_key(p, q)
sage: C = ([[1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0], \
... [1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1], \
... [0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0], \
... [0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1], \
... [1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0], \
... [0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1], \
... [1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0], \
... [1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1], \
... [0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0], \
... [1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1], \
... [1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1], \
... [1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0], \
... [0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1]], 3479653279)
sage: P = bg.decrypt(C, K)
sage: bin_to_ascii(flatten(P))
'Blum-Goldwasser encryption'
TESTS:
The private key 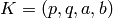 must be such that
must be such that  and
and  are
distinct Blum primes. Even if
are
distinct Blum primes. Even if  and
and  pass this criterion, they
must also satisfy the requirement
pass this criterion, they
must also satisfy the requirement 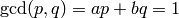 .
.
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: C = ([[0, 0, 1, 0], [0, 0, 0, 0], [1, 1, 0, 0], [1, 1, 1, 0], [0, 1, 0, 0]], 139680)
sage: K = (7, 7, 1, 2)
sage: bg.decrypt(C, K)
...
ValueError: p and q must be distinct Blum primes.
sage: K = (7, 23, 1, 2)
sage: bg.decrypt(C, K)
...
ValueError: a and b must satisfy gcd(p, q) = ap + bq = 1.
sage: K = (11, 29, 8, -3)
sage: bg.decrypt(C, K)
...
ValueError: p and q must be distinct Blum primes.
Apply the Blum-Goldwasser scheme to encrypt the plaintext P using the public key K.
INPUT:
 and
and  are Blum primes and
are Blum primes and
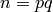 is a public key, then seed is a quadratic residue in
the multiplicative group
is a public key, then seed is a quadratic residue in
the multiplicative group 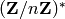 . If seed=None,
then the function would generate its own random quadratic residue
in
. If seed=None,
then the function would generate its own random quadratic residue
in 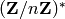 . Where a value for seed is provided,
it is your responsibility to ensure that the seed is a
quadratic residue in the multiplicative group
. Where a value for seed is provided,
it is your responsibility to ensure that the seed is a
quadratic residue in the multiplicative group 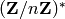 .
.OUTPUT:
 is of the form
is of the form
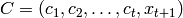 . Each
. Each 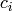 is a
sub-block of binary string and
is a
sub-block of binary string and 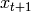 is the result of the
is the result of the
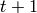 -th iteration of the Blum-Blum-Shub algorithm.
-th iteration of the Blum-Blum-Shub algorithm.ALGORITHM:
The Blum-Goldwasser encryption algorithm is described in Algorithm 8.56, page 309 of [MenezesEtAl1996]. The algorithm works as follows:
 be a public key, where
be a public key, where 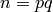 is the product of two
distinct Blum primes
is the product of two
distinct Blum primes  and
and  .
.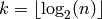 and
and
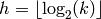 .
.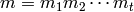 be the message (plaintext) where
each
be the message (plaintext) where
each 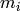 is a binary string of length
is a binary string of length 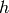 .
.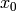 , which is a quadratic residue in
the multiplicative group
, which is a quadratic residue in
the multiplicative group 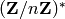 . That is, choose
a random
. That is, choose
a random 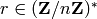 and compute
and compute
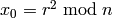 .
. from 1 to
from 1 to  , do:
, do: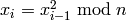 .
.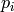 be the
be the 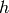 least significant bits of
least significant bits of 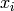 .
.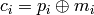 .
.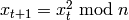 .
.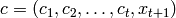 .
.The value 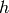 in the algorithm is the sub-block length. If the
binary string representing the message cannot be divided into blocks
of length
in the algorithm is the sub-block length. If the
binary string representing the message cannot be divided into blocks
of length 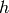 each, then other sub-block lengths would be used
instead. The sub-block lengths to fall back on are in the
following order: 16, 8, 4, 2, 1.
each, then other sub-block lengths would be used
instead. The sub-block lengths to fall back on are in the
following order: 16, 8, 4, 2, 1.
EXAMPLES:
The following encryption example is taken from Example 8.57, pages 309–310 of [MenezesEtAl1996]. Here, we encrypt a binary string:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: p = 499; q = 547; n = p * q
sage: P = "10011100000100001100"
sage: C = bg.encrypt(P, n, seed=159201); C
([[0, 0, 1, 0], [0, 0, 0, 0], [1, 1, 0, 0], [1, 1, 1, 0], [0, 1, 0, 0]], 139680)
Convert the ciphertext sub-blocks into a binary string:
sage: bin = BinaryStrings()
sage: bin(flatten(C[0]))
00100000110011100100
Now encrypt an ASCII string. The result is random; no seed is provided to the encryption function so the function generates its own random seed:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: K = 32300619509
sage: P = "Blum-Goldwasser encryption"
sage: bg.encrypt(P, K) # random
([[1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0], \
[1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1], \
[0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0], \
[0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1], \
[1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0], \
[0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1], \
[1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0], \
[1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1], \
[0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0], \
[1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1], \
[1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1], \
[1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0], \
[0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1]], 3479653279)
TESTS:
The plaintext cannot be an empty string.
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: bg.encrypt("", 3)
...
ValueError: The plaintext cannot be an empty string.
Return the Blum-Goldwasser private key corresponding to the distinct Blum primes p and q.
INPUT:
OUTPUT:
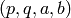 where
where
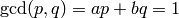 .
.Both p and q must be distinct Blum primes. Let  be a
positive prime. Then
be a
positive prime. Then  is a Blum prime if
is a Blum prime if  is congruent to 3
modulo 4, i.e.
is congruent to 3
modulo 4, i.e. 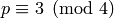 .
.
EXAMPLES:
Obtain two distinct Blum primes and compute the Blum-Goldwasser private key corresponding to those two Blum primes:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: from sage.crypto.util import is_blum_prime
sage: bg = BlumGoldwasser()
sage: P = primes_first_n(10); P
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
sage: map(is_blum_prime, P)
[False, True, False, True, True, False, False, True, True, False]
sage: bg.private_key(19, 23)
(19, 23, -6, 5)
Choose two distinct random Blum primes, compute the Blum-Goldwasser
private key corresponding to those two primes, and test that the
resulting private key 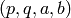 satisfies
satisfies
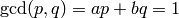 :
:
sage: from sage.crypto.util import random_blum_prime
sage: p = random_blum_prime(10**4, 10**5)
sage: q = random_blum_prime(10**4, 10**5)
sage: while q == p:
... q = random_blum_prime(10**4, 10**5)
...
sage: p, q, a, b = bg.private_key(p, q)
sage: gcd(p, q) == a*p + b*q == 1
True
TESTS:
Both of the input p and q must be distinct Blum primes.
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: bg.private_key(78307, 78307)
...
ValueError: p and q must be distinct Blum primes.
sage: bg.private_key(7, 4)
...
ValueError: p and q must be distinct Blum primes.
Return the Blum-Goldwasser public key corresponding to the distinct Blum primes p and q.
INPUT:
OUTPUT:
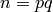 .
.Both p and q must be distinct Blum primes. Let  be a
positive prime. Then
be a
positive prime. Then  is a Blum prime if
is a Blum prime if  is congruent to 3
modulo 4, i.e.
is congruent to 3
modulo 4, i.e. 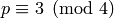 .
.
EXAMPLES:
Obtain two distinct Blum primes and compute the Blum-Goldwasser public key corresponding to those two Blum primes:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: from sage.crypto.util import is_blum_prime
sage: bg = BlumGoldwasser()
sage: P = primes_first_n(10); P
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
sage: map(is_blum_prime, P)
[False, True, False, True, True, False, False, True, True, False]
sage: bg.public_key(3, 7)
21
Choose two distinct random Blum primes, compute the Blum-Goldwasser public key corresponding to those two primes, and test that the public key factorizes into Blum primes:
sage: from sage.crypto.util import random_blum_prime
sage: p = random_blum_prime(10**4, 10**5)
sage: q = random_blum_prime(10**4, 10**5)
sage: while q == p:
... q = random_blum_prime(10**4, 10**5)
...
sage: n = bg.public_key(p, q)
sage: f = factor(n)
sage: is_blum_prime(f[0][0]); is_blum_prime(f[1][0])
True
True
sage: p * q == f[0][0] * f[1][0]
True
TESTS:
The input p and q must be distinct Blum primes.
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: bg.public_key(3, 3)
...
ValueError: p and q must be distinct Blum primes.
sage: bg.public_key(23, 29)
...
ValueError: p and q must be distinct Blum primes.
Return a pair of random public and private keys.
INPUT:
 and
and  can be. So we have
0 < lower_bound <= p, q <= upper_bound. The lower bound must
be distinct from the upper bound.
can be. So we have
0 < lower_bound <= p, q <= upper_bound. The lower bound must
be distinct from the upper bound. and
and  can be. So we have
0 < lower_bound <= p, q <= upper_bound. The lower bound must
be distinct from the upper bound.
can be. So we have
0 < lower_bound <= p, q <= upper_bound. The lower bound must
be distinct from the upper bound.OUTPUT:
 and
and  are guaranteed to be Blum primes. The
public key is
are guaranteed to be Blum primes. The
public key is 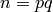 , and the private key is
, and the private key is 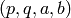 where
where
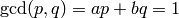 .
.ALGORITHM:
The key generation algorithm is described in Algorithm 8.55, page 308 of [MenezesEtAl1996]. The algorithm works as follows:
 and
and  be distinct large random primes, each congruent
to 3 modulo 4. That is,
be distinct large random primes, each congruent
to 3 modulo 4. That is,  and
and  are Blum primes.
are Blum primes.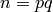 be the product of
be the product of  and
and  .
. and
and
 such that
such that 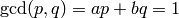 .
. and the corresponding private key is
and the corresponding private key is
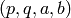 .
.Note
Beware that there might not be any primes between the lower and upper bounds. So make sure that these two bounds are “sufficiently” far apart from each other for there to be primes congruent to 3 modulo 4. In particular, there should be at least two distinct primes within these bounds, each prime being congruent to 3 modulo 4.
EXAMPLES:
Choosing a random pair of public and private keys. We then test to see if they satisfy the requirements of the Blum-Goldwasser scheme:
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: from sage.crypto.util import is_blum_prime
sage: bg = BlumGoldwasser()
sage: pubkey, prikey = bg.random_key(10**4, 10**5)
sage: p, q, a, b = prikey
sage: is_blum_prime(p); is_blum_prime(q)
True
True
sage: p == q
False
sage: pubkey == p*q
True
sage: gcd(p, q) == a*p + b*q == 1
True
TESTS:
Make sure that there is at least one Blum prime between the lower and upper bounds. In the following example, we have lbound=24 and ubound=30 with 29 being the only prime within those bounds. But 29 is not a Blum prime.
sage: from sage.crypto.public_key.blum_goldwasser import BlumGoldwasser
sage: bg = BlumGoldwasser()
sage: pubkey, privkey = bg.random_key(24, 30)
...
ValueError: No Blum primes within the specified closed interval.