Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Cryptography »

A simplified variant of the Advanced Encryption Standard (AES). Note that Mini-AES is for educational purposes only. It is a small-scale version of the AES designed to help beginners understand the basic structure of AES.
AUTHORS:
Bases: sage.structure.sage_object.SageObject
This class implements the Mini Advanced Encryption Standard (Mini-AES) described in [P02]. Note that Phan’s Mini-AES is for educational purposes only and is not secure for practical purposes. Mini-AES is a version of the AES with all parameters significantly reduced, but at the same time preserving the structure of AES. The goal of Mini-AES is to allow a beginner to understand the structure of AES, thus laying a foundation for a thorough study of AES. Its goal is as a teaching tool and is different from the SR small scale variants of the AES. SR defines a family of parameterizable variants of the AES suitable as a framework for comparing different cryptanalytic techniques that can be brought to bear on the AES.
EXAMPLES:
Encrypt a plaintext:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: P = MS([K("x^3 + x"), K("x^2 + 1"), K("x^2 + x"), K("x^3 + x^2")]); P
<BLANKLINE>
[ x^3 + x x^2 + 1]
[ x^2 + x x^3 + x^2]
sage: key = MS([K("x^3 + x^2"), K("x^3 + x"), K("x^3 + x^2 + x"), K("x^2 + x + 1")]); key
<BLANKLINE>
[ x^3 + x^2 x^3 + x]
[x^3 + x^2 + x x^2 + x + 1]
sage: C = maes.encrypt(P, key); C
<BLANKLINE>
[ x x^2 + x]
[x^3 + x^2 + x x^3 + x]
Decrypt the result:
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt; P
<BLANKLINE>
[ x^3 + x x^2 + 1]
[ x^2 + x x^3 + x^2]
<BLANKLINE>
[ x^3 + x x^2 + 1]
[ x^2 + x x^3 + x^2]
sage: plaintxt == P
True
We can also work directly with binary strings:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: bin = BinaryStrings()
sage: key = bin.encoding("KE"); key
0100101101000101
sage: P = bin.encoding("Encrypt this secret message!"); P
01000101011011100110001101110010011110010111000001110100001000000111010001101000011010010111001100100000011100110110010101100011011100100110010101110100001000000110110101100101011100110111001101100001011001110110010100100001
sage: C = maes(P, key, algorithm="encrypt"); C
10001000101001101111000001111000010011001110110101000111011011010101001011101111101011001110011100100011101100101010100010100111110110011001010001000111011011010010000011000110001100000111000011100110101111000000001110001001
sage: plaintxt = maes(C, key, algorithm="decrypt")
sage: plaintxt == P
True
Now we work with integers  such that
such that 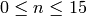 :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: P = [n for n in xrange(16)]; P
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
sage: key = [2, 3, 11, 0]; key
[2, 3, 11, 0]
sage: P = maes.integer_to_binary(P); P
0000000100100011010001010110011110001001101010111100110111101111
sage: key = maes.integer_to_binary(key); key
0010001110110000
sage: C = maes(P, key, algorithm="encrypt"); C
1100100000100011111001010101010101011011100111110001000011100001
sage: plaintxt = maes(C, key, algorithm="decrypt")
sage: plaintxt == P
True
Generate some random plaintext and a random secret key. Encrypt the plaintext using that secret key and decrypt the result. Then compare the decrypted plaintext with the original plaintext:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: MS = MatrixSpace(FiniteField(16, "x"), 2, 2)
sage: P = MS.random_element()
sage: key = maes.random_key()
sage: C = maes.encrypt(P, key)
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt == P
True
REFERENCES:
| [P02] | R. C.-W. Phan. Mini advanced encryption standard (mini-AES): a testbed for cryptanalysis students. Cryptologia, 26(4):283–306, 2002. |
Return the binary representation of G.
If G is an element of the finite field  , then
obtain the binary representation of G. If G is a list of
elements belonging to
, then
obtain the binary representation of G. If G is a list of
elements belonging to  , obtain the 4-bit
representation of each element of the list, then concatenate the
resulting 4-bit strings into a binary string. If G is a matrix
with entries over
, obtain the 4-bit
representation of each element of the list, then concatenate the
resulting 4-bit strings into a binary string. If G is a matrix
with entries over  , convert each matrix entry to its
4-bit representation, then concatenate the 4-bit strings. The
concatenation is performed starting from the top-left corner of the
matrix, working across left to right, top to bottom. Each element of
, convert each matrix entry to its
4-bit representation, then concatenate the 4-bit strings. The
concatenation is performed starting from the top-left corner of the
matrix, working across left to right, top to bottom. Each element of
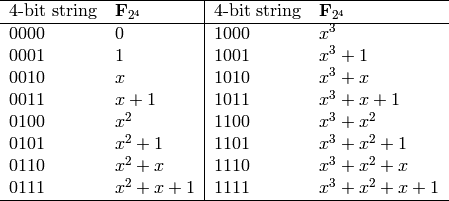
 can be associated with a unique 4-bit string
according to the following table:
can be associated with a unique 4-bit string
according to the following table:
INPUT:
 , a list of elements of
, a list of elements of
 , or a matrix over
, or a matrix over 
OUTPUT:
EXAMPLES:
Obtain the binary representation of all elements of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: S = Set(K); len(S) # GF(2^4) has this many elements
16
sage: [maes.GF_to_binary(S[i]) for i in xrange(len(S))]
<BLANKLINE>
[0000,
0001,
0010,
0011,
0100,
0101,
0110,
0111,
1000,
1001,
1010,
1011,
1100,
1101,
1110,
1111]
The binary representation of a list of elements belonging to
 :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: G = [K("x^2 + x + 1"), K("x^3 + x^2"), K("x"), K("x^3 + x + 1"), K("x^3 + x^2 + x + 1"), K("x^2 + x"), K("1"), K("x^2 + x + 1")]
sage: maes.GF_to_binary(G)
01111100001010111111011000010111
The binary representation of a matrix over  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: G = MS([K("x^3 + x^2"), K("x + 1"), K("x^2 + x + 1"), K("x^3 + x^2 + x")]); G
<BLANKLINE>
[ x^3 + x^2 x + 1]
[ x^2 + x + 1 x^3 + x^2 + x]
sage: maes.GF_to_binary(G)
1100001101111110
sage: MS = MatrixSpace(K, 2, 4)
sage: G = MS([K("x^2 + x + 1"), K("x^3 + x^2"), K("x"), K("x^3 + x + 1"), K("x^3 + x^2 + x + 1"), K("x^2 + x"), K("1"), K("x^2 + x + 1")]); G
<BLANKLINE>
[ x^2 + x + 1 x^3 + x^2 x x^3 + x + 1]
[x^3 + x^2 + x + 1 x^2 + x 1 x^2 + x + 1]
sage: maes.GF_to_binary(G)
01111100001010111111011000010111
TESTS:
Input must be an element of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(8, "x")
sage: G = K.random_element()
sage: maes.GF_to_binary(G)
...
TypeError: input G must be an element of GF(16), a list of elements of GF(16), or a matrix over GF(16)
A list of elements belonging to  :
:
sage: maes.GF_to_binary([])
...
ValueError: input G must be an element of GF(16), a list of elements of GF(16), or a matrix over GF(16)
sage: G = [K.random_element() for i in xrange(5)]
sage: maes.GF_to_binary(G)
...
KeyError:...
A matrix over  :
:
sage: MS = MatrixSpace(FiniteField(7, "x"), 4, 5)
sage: maes.GF_to_binary(MS.random_element())
...
TypeError: input G must be an element of GF(16), a list of elements of GF(16), or a matrix over GF(16)
Return the integer representation of the finite field element G.
If G is an element of the finite field  , then
obtain the integer representation of G. If G is a list of
elements belonging to
, then
obtain the integer representation of G. If G is a list of
elements belonging to  , obtain the integer
representation of each element of the list, and return the result
as a list of integers. If G is a matrix with entries over
, obtain the integer
representation of each element of the list, and return the result
as a list of integers. If G is a matrix with entries over
 , convert each matrix entry to its integer representation,
and return the result as a list of integers. The resulting list is
obtained by starting from the top-left corner of the matrix, working
across left to right, top to bottom. Each element of
, convert each matrix entry to its integer representation,
and return the result as a list of integers. The resulting list is
obtained by starting from the top-left corner of the matrix, working
across left to right, top to bottom. Each element of  can
be associated with a unique integer according to the following table:
can
be associated with a unique integer according to the following table:

INPUT:
 , a list of elements belonging to
, a list of elements belonging to
 , or a matrix over
, or a matrix over 
OUTPUT:
EXAMPLES:
Obtain the integer representation of all elements of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: S = Set(K); len(S) # GF(2^4) has this many elements
16
sage: [maes.GF_to_integer(S[i]) for i in xrange(len(S))]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
The integer representation of a list of elements belonging to
 :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: G = [K("x^2 + x + 1"), K("x^3 + x^2"), K("x"), K("x^3 + x + 1"), K("x^3 + x^2 + x + 1"), K("x^2 + x"), K("1"), K("x^2 + x + 1")]
sage: maes.GF_to_integer(G)
[7, 12, 2, 11, 15, 6, 1, 7]
The integer representation of a matrix over  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: G = MS([K("x^3 + x^2"), K("x + 1"), K("x^2 + x + 1"), K("x^3 + x^2 + x")]); G
<BLANKLINE>
[ x^3 + x^2 x + 1]
[ x^2 + x + 1 x^3 + x^2 + x]
sage: maes.GF_to_integer(G)
[12, 3, 7, 14]
sage: MS = MatrixSpace(K, 2, 4)
sage: G = MS([K("x^2 + x + 1"), K("x^3 + x^2"), K("x"), K("x^3 + x + 1"), K("x^3 + x^2 + x + 1"), K("x^2 + x"), K("1"), K("x^2 + x + 1")]); G
<BLANKLINE>
[ x^2 + x + 1 x^3 + x^2 x x^3 + x + 1]
[x^3 + x^2 + x + 1 x^2 + x 1 x^2 + x + 1]
sage: maes.GF_to_integer(G)
[7, 12, 2, 11, 15, 6, 1, 7]
TESTS:
Input must be an element of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(7, "x")
sage: G = K.random_element()
sage: maes.GF_to_integer(G)
...
TypeError: input G must be an element of GF(16), a list of elements of GF(16), or a matrix over GF(16)
A list of elements belonging to  :
:
sage: maes.GF_to_integer([])
...
ValueError: input G must be an element of GF(16), a list of elements of GF(16), or a matrix over GF(16)
sage: G = [K.random_element() for i in xrange(5)]
sage: maes.GF_to_integer(G)
...
KeyError:...
A matrix over  :
:
sage: MS = MatrixSpace(FiniteField(7, "x"), 4, 5)
sage: maes.GF_to_integer(MS.random_element())
...
TypeError: input G must be an element of GF(16), a list of elements of GF(16), or a matrix over GF(16)
Return the matrix addition of block and rkey. Both block
and rkey are  matrices over the finite field
matrices over the finite field
 . This method just return the matrix addition of
these two matrices.
. This method just return the matrix addition of
these two matrices.
INPUT:
 matrix with entries over
matrix with entries over

 matrix with entries over
matrix with entries over

OUTPUT:
EXAMPLES:
We can work with elements of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: D = MS([ [K("x^3 + x^2 + x + 1"), K("x^3 + x")], [K("0"), K("x^3 + x^2")] ]); D
<BLANKLINE>
[x^3 + x^2 + x + 1 x^3 + x]
[ 0 x^3 + x^2]
sage: k = MS([ [K("x^2 + 1"), K("x^3 + x^2 + x + 1")], [K("x + 1"), K("0")] ]); k
<BLANKLINE>
[ x^2 + 1 x^3 + x^2 + x + 1]
[ x + 1 0]
sage: maes.add_key(D, k)
<BLANKLINE>
[ x^3 + x x^2 + 1]
[ x + 1 x^3 + x^2]
Or work with binary strings:
sage: bin = BinaryStrings()
sage: B = bin.encoding("We"); B
0101011101100101
sage: B = MS(maes.binary_to_GF(B)); B
<BLANKLINE>
[ x^2 + 1 x^2 + x + 1]
[ x^2 + x x^2 + 1]
sage: key = bin.encoding("KY"); key
0100101101011001
sage: key = MS(maes.binary_to_GF(key)); key
<BLANKLINE>
[ x^2 x^3 + x + 1]
[ x^2 + 1 x^3 + 1]
sage: maes.add_key(B, key)
<BLANKLINE>
[ 1 x^3 + x^2]
[ x + 1 x^3 + x^2]
We can also work with integers  such that
such that 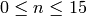 :
:
sage: N = [2, 3, 5, 7]; N
[2, 3, 5, 7]
sage: key = [9, 11, 13, 15]; key
[9, 11, 13, 15]
sage: N = MS(maes.integer_to_GF(N)); N
<BLANKLINE>
[ x x + 1]
[ x^2 + 1 x^2 + x + 1]
sage: key = MS(maes.integer_to_GF(key)); key
<BLANKLINE>
[ x^3 + 1 x^3 + x + 1]
[ x^3 + x^2 + 1 x^3 + x^2 + x + 1]
sage: maes.add_key(N, key)
<BLANKLINE>
[x^3 + x + 1 x^3]
[ x^3 x^3]
TESTS:
The input block and key must each be a matrix:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MSB = MatrixSpace(K, 2, 2)
sage: B = MSB([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ])
sage: maes.add_key(B, "key")
...
TypeError: round key must be a 2 x 2 matrix over GF(16)
sage: maes.add_key("block", "key")
...
TypeError: input block must be a 2 x 2 matrix over GF(16)
In addition, the dimensions of the input matrices must each be
 :
:
sage: MSB = MatrixSpace(K, 1, 2)
sage: B = MSB([ [K("x^3 + 1"), K("x^2 + x")] ])
sage: maes.add_key(B, "key")
...
TypeError: input block must be a 2 x 2 matrix over GF(16)
sage: MSB = MatrixSpace(K, 2, 2)
sage: B = MSB([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ])
sage: MSK = MatrixSpace(K, 1, 2)
sage: key = MSK([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")]])
sage: maes.add_key(B, key)
...
TypeError: round key must be a 2 x 2 matrix over GF(16)
Return a list of elements of  that represents the
binary string B. The number of bits in B must be greater
than zero and a multiple of 4. Each nibble (or 4-bit string) is
uniquely associated with an element of
that represents the
binary string B. The number of bits in B must be greater
than zero and a multiple of 4. Each nibble (or 4-bit string) is
uniquely associated with an element of  as
specified by the following table:
as
specified by the following table:

INPUT:
OUTPUT:
 that
represent the binary string B.
that
represent the binary string B.EXAMPLES:
Obtain all the elements of the finite field  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: bin = BinaryStrings()
sage: B = bin("0000000100100011010001010110011110001001101010111100110111101111")
sage: maes.binary_to_GF(B)
<BLANKLINE>
[0,
1,
x,
x + 1,
x^2,
x^2 + 1,
x^2 + x,
x^2 + x + 1,
x^3,
x^3 + 1,
x^3 + x,
x^3 + x + 1,
x^3 + x^2,
x^3 + x^2 + 1,
x^3 + x^2 + x,
x^3 + x^2 + x + 1]
TESTS:
The input B must be a non-empty binary string, where the number of bits is a multiple of 4:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.binary_to_GF("")
...
ValueError: the number of bits in the binary string B must be positive and a multiple of 4
sage: maes.binary_to_GF("101")
...
ValueError: the number of bits in the binary string B must be positive and a multiple of 4
Return a list of integers representing the binary string B. The number of bits in B must be greater than zero and a multiple of 4. Each nibble (or 4-bit string) is uniquely associated with an integer as specified by the following table:

INPUT:
OUTPUT:
EXAMPLES:
Obtain the integer representation of every 4-bit string:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: bin = BinaryStrings()
sage: B = bin("0000000100100011010001010110011110001001101010111100110111101111")
sage: maes.binary_to_integer(B)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
TESTS:
The input B must be a non-empty binary string, where the number of bits is a multiple of 4:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.binary_to_integer("")
...
ValueError: the number of bits in the binary string B must be positive and a multiple of 4
sage: maes.binary_to_integer("101")
...
ValueError: the number of bits in the binary string B must be positive and a multiple of 4
Return the block length of Phan’s Mini-AES block cipher. A key in
Phan’s Mini-AES is a block of 16 bits. Each nibble of a key can be
considered as an element of the finite field  .
Therefore the key consists of four elements from
.
Therefore the key consists of four elements from  .
.
OUTPUT:
EXAMPLES:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.block_length()
16
Use Phan’s Mini-AES to decrypt the ciphertext C with the secret
key key. Both C and key must be  matrices over
the finite field
matrices over
the finite field  . Let
. Let 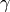 denote the
operation of nibble-sub,
denote the
operation of nibble-sub, 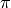 denote shift-row,
denote shift-row, 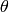 denote
mix-column, and
denote
mix-column, and 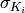 denote add-key with the round key
denote add-key with the round key
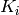 . Then decryption
. Then decryption  using Phan’s Mini-AES is the function
composition
using Phan’s Mini-AES is the function
composition
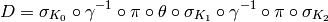
where 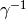 is the nibble-sub operation that uses the S-box
for decryption, and the order of execution is from right to left.
is the nibble-sub operation that uses the S-box
for decryption, and the order of execution is from right to left.
INPUT:
 matrix over
the finite field
matrix over
the finite field 
 matrix over the finite field
matrix over the finite field 
OUTPUT:
EXAMPLES:
We encrypt a plaintext, decrypt the ciphertext, then compare the
decrypted plaintext with the original plaintext. Here we work with
elements of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: P = MS([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ]); P
<BLANKLINE>
[ x^3 + 1 x^2 + x]
[x^3 + x^2 x + 1]
sage: key = MS([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")], [K("x + 1"), K("0")] ]); key
<BLANKLINE>
[ x^3 + x^2 x^3 + x^2 + x + 1]
[ x + 1 0]
sage: C = maes.encrypt(P, key); C
<BLANKLINE>
[x^2 + x + 1 x^3 + x^2]
[ x x^2 + x]
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt; P
<BLANKLINE>
[ x^3 + 1 x^2 + x]
[x^3 + x^2 x + 1]
<BLANKLINE>
[ x^3 + 1 x^2 + x]
[x^3 + x^2 x + 1]
sage: plaintxt == P
True
But we can also work with binary strings:
sage: bin = BinaryStrings()
sage: P = bin.encoding("de"); P
0110010001100101
sage: P = MS(maes.binary_to_GF(P)); P
<BLANKLINE>
[x^2 + x x^2]
[x^2 + x x^2 + 1]
sage: key = bin.encoding("ke"); key
0110101101100101
sage: key = MS(maes.binary_to_GF(key)); key
<BLANKLINE>
[ x^2 + x x^3 + x + 1]
[ x^2 + x x^2 + 1]
sage: C = maes.encrypt(P, key)
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt == P
True
Here we work with integers  such that
such that 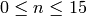 :
:
sage: P = [3, 5, 7, 14]; P
[3, 5, 7, 14]
sage: key = [2, 6, 7, 8]; key
[2, 6, 7, 8]
sage: P = MS(maes.integer_to_GF(P)); P
<BLANKLINE>
[ x + 1 x^2 + 1]
[ x^2 + x + 1 x^3 + x^2 + x]
sage: key = MS(maes.integer_to_GF(key)); key
<BLANKLINE>
[ x x^2 + x]
[x^2 + x + 1 x^3]
sage: C = maes.encrypt(P, key)
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt == P
True
TESTS:
The input block must be a matrix:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: key = MS([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")], [K("x + 1"), K("0")] ])
sage: maes.decrypt("C", key)
...
TypeError: ciphertext block must be a 2 x 2 matrix over GF(16)
sage: C = MS([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ])
sage: maes.decrypt(C, "key")
...
TypeError: secret key must be a 2 x 2 matrix over GF(16)
In addition, the dimensions of the input matrices must be
 :
:
sage: MS = MatrixSpace(K, 1, 2)
sage: C = MS([ [K("x^3 + 1"), K("x^2 + x")]])
sage: maes.decrypt(C, "key")
...
TypeError: ciphertext block must be a 2 x 2 matrix over GF(16)
sage: MSC = MatrixSpace(K, 2, 2)
sage: C = MSC([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ])
sage: MSK = MatrixSpace(K, 1, 2)
sage: key = MSK([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")]])
sage: maes.decrypt(C, key)
...
TypeError: secret key must be a 2 x 2 matrix over GF(16)
Use Phan’s Mini-AES to encrypt the plaintext P with the secret
key key. Both P and key must be  matrices
over the finite field
matrices
over the finite field  . Let
. Let 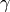 denote the
operation of nibble-sub,
denote the
operation of nibble-sub, 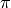 denote shift-row,
denote shift-row, 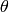 denote
mix-column, and
denote
mix-column, and 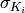 denote add-key with the round key
denote add-key with the round key
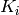 . Then encryption
. Then encryption  using Phan’s Mini-AES is the function
composition
using Phan’s Mini-AES is the function
composition
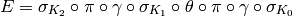
where the order of execution is from right to left. Note that
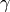 is the nibble-sub operation that uses the S-box for
encryption.
is the nibble-sub operation that uses the S-box for
encryption.
INPUT:
 matrix over
the finite field
matrix over
the finite field 
 matrix over the finite field
matrix over the finite field 
OUTPUT:
EXAMPLES:
Here we work with elements of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: P = MS([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ]); P
<BLANKLINE>
[ x^3 + 1 x^2 + x]
[x^3 + x^2 x + 1]
sage: key = MS([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")], [K("x + 1"), K("0")] ]); key
<BLANKLINE>
[ x^3 + x^2 x^3 + x^2 + x + 1]
[ x + 1 0]
sage: maes.encrypt(P, key)
<BLANKLINE>
[x^2 + x + 1 x^3 + x^2]
[ x x^2 + x]
But we can also work with binary strings:
sage: bin = BinaryStrings()
sage: P = bin.encoding("de"); P
0110010001100101
sage: P = MS(maes.binary_to_GF(P)); P
<BLANKLINE>
[x^2 + x x^2]
[x^2 + x x^2 + 1]
sage: key = bin.encoding("ke"); key
0110101101100101
sage: key = MS(maes.binary_to_GF(key)); key
<BLANKLINE>
[ x^2 + x x^3 + x + 1]
[ x^2 + x x^2 + 1]
sage: C = maes.encrypt(P, key)
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt == P
True
Now we work with integers  such that
such that 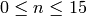 :
:
sage: P = [1, 5, 8, 12]; P
[1, 5, 8, 12]
sage: key = [5, 9, 15, 0]; key
[5, 9, 15, 0]
sage: P = MS(maes.integer_to_GF(P)); P
<BLANKLINE>
[ 1 x^2 + 1]
[ x^3 x^3 + x^2]
sage: key = MS(maes.integer_to_GF(key)); key
<BLANKLINE>
[ x^2 + 1 x^3 + 1]
[x^3 + x^2 + x + 1 0]
sage: C = maes.encrypt(P, key)
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt == P
True
TESTS:
The input block must be a matrix:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: key = MS([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")], [K("x + 1"), K("0")] ])
sage: maes.encrypt("P", key)
...
TypeError: plaintext block must be a 2 x 2 matrix over GF(16)
sage: P = MS([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ])
sage: maes.encrypt(P, "key")
...
TypeError: secret key must be a 2 x 2 matrix over GF(16)
In addition, the dimensions of the input matrices must be
 :
:
sage: MS = MatrixSpace(K, 1, 2)
sage: P = MS([ [K("x^3 + 1"), K("x^2 + x")]])
sage: maes.encrypt(P, "key")
...
TypeError: plaintext block must be a 2 x 2 matrix over GF(16)
sage: MSP = MatrixSpace(K, 2, 2)
sage: P = MSP([ [K("x^3 + 1"), K("x^2 + x")], [K("x^3 + x^2"), K("x + 1")] ])
sage: MSK = MatrixSpace(K, 1, 2)
sage: key = MSK([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")]])
sage: maes.encrypt(P, key)
...
TypeError: secret key must be a 2 x 2 matrix over GF(16)
Return the finite field representation of N. If  is an
integer such that
is an
integer such that 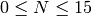 , return the element of
, return the element of
 that represents N. If N is a list of integers
each of which is
that represents N. If N is a list of integers
each of which is 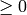 and
and 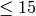 , then obtain the element
of
, then obtain the element
of  that represents each such integer, and return a list
of such finite field representations. Each integer between 0 and 15,
inclusive, can be associated with a unique element of
that represents each such integer, and return a list
of such finite field representations. Each integer between 0 and 15,
inclusive, can be associated with a unique element of  according to the following table:
according to the following table:

INPUT:
OUTPUT:
 .
.EXAMPLES:
Obtain the element of  representing an integer
representing an integer  , where
, where
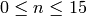 :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.integer_to_GF(0)
0
sage: maes.integer_to_GF(2)
x
sage: maes.integer_to_GF(7)
x^2 + x + 1
Obtain the finite field elements corresponding to all non-negative integers less than or equal to 15:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: lst = [n for n in xrange(16)]; lst
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
sage: maes.integer_to_GF(lst)
<BLANKLINE>
[0,
1,
x,
x + 1,
x^2,
x^2 + 1,
x^2 + x,
x^2 + x + 1,
x^3,
x^3 + 1,
x^3 + x,
x^3 + x + 1,
x^3 + x^2,
x^3 + x^2 + 1,
x^3 + x^2 + x,
x^3 + x^2 + x + 1]
TESTS:
The input N can be an integer, but it must be such that
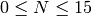 :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.integer_to_GF(-1)
...
KeyError:...
sage: maes.integer_to_GF(16)
...
KeyError:...
sage: maes.integer_to_GF("2")
...
TypeError: N must be an integer 0 <= N <= 15 or a list of such integers
The input N can be a list of integers, but each integer  in
the list must be bounded such that
in
the list must be bounded such that 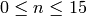 :
:
sage: maes.integer_to_GF([])
...
ValueError: N must be an integer 0 <= N <= 15 or a list of such integers
sage: maes.integer_to_GF([""])
...
KeyError:...
sage: maes.integer_to_GF([0, 2, 3, "4"])
...
KeyError:...
sage: maes.integer_to_GF([0, 2, 3, 16])
...
KeyError:...
Return the binary representation of N. If  is an integer such
that
is an integer such
that 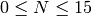 , return the binary representation of N.
If N is a list of integers each of which is
, return the binary representation of N.
If N is a list of integers each of which is 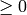 and
and
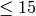 , then obtain the binary representation of each integer,
and concatenate the individual binary representations into a single
binary string. Each integer between 0 and 15, inclusive, can be
associated with a unique 4-bit string according to the following
table:
, then obtain the binary representation of each integer,
and concatenate the individual binary representations into a single
binary string. Each integer between 0 and 15, inclusive, can be
associated with a unique 4-bit string according to the following
table:

INPUT:
OUTPUT:
EXAMPLES:
The binary representations of all integers between 0 and 15, inclusive:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: lst = [n for n in xrange(16)]; lst
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
sage: maes.integer_to_binary(lst)
0000000100100011010001010110011110001001101010111100110111101111
The binary representation of an integer between 0 and 15, inclusive:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.integer_to_binary(3)
0011
sage: maes.integer_to_binary(5)
0101
sage: maes.integer_to_binary(7)
0111
TESTS:
The input N can be an integer, but must be bounded such that
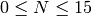 :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.integer_to_binary(-1)
...
KeyError:...
sage: maes.integer_to_binary("1")
...
TypeError: N must be an integer 0 <= N <= 15 or a list of such integers
sage: maes.integer_to_binary("")
...
TypeError: N must be an integer 0 <= N <= 15 or a list of such integers
The input N can be a list of integers, but each integer  of
the list must be
of
the list must be 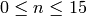 :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.integer_to_binary([])
...
ValueError: N must be an integer 0 <= N <= 15 or a list of such integers
sage: maes.integer_to_binary([""])
...
KeyError:...
sage: maes.integer_to_binary([0, 1, 2, 16])
...
KeyError:...
Return the matrix multiplication of block with a constant matrix. The constant matrix is
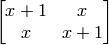
If the input block is
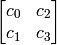
then the output block is
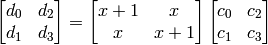
INPUT:
 matrix with entries over
matrix with entries over

OUTPUT:
 matrix resulting from multiplying the above constant
matrix with the input matrix block.
matrix resulting from multiplying the above constant
matrix with the input matrix block.EXAMPLES:
Here we work with elements of  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: mat = MS([ [K("x^2 + x + 1"), K("x^3 + x^2 + 1")], [K("x^3"), K("x")] ])
sage: maes.mix_column(mat)
<BLANKLINE>
[ x^3 + x 0]
[ x^2 + 1 x^3 + x^2 + x + 1]
Multiplying by the identity matrix should leave the constant matrix unchanged:
sage: eye = MS([ [K("1"), K("0")], [K("0"), K("1")] ])
sage: maes.mix_column(eye)
<BLANKLINE>
[x + 1 x]
[ x x + 1]
We can also work with binary strings:
sage: bin = BinaryStrings()
sage: B = bin.encoding("rT"); B
0111001001010100
sage: B = MS(maes.binary_to_GF(B)); B
<BLANKLINE>
[x^2 + x + 1 x]
[ x^2 + 1 x^2]
sage: maes.mix_column(B)
<BLANKLINE>
[ x + 1 x^3 + x^2 + x]
[ 1 x^3]
We can also work with integers  such that
such that 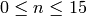 :
:
sage: P = [10, 5, 2, 7]; P
[10, 5, 2, 7]
sage: P = MS(maes.integer_to_GF(P)); P
<BLANKLINE>
[ x^3 + x x^2 + 1]
[ x x^2 + x + 1]
sage: maes.mix_column(P)
<BLANKLINE>
[x^3 + 1 1]
[ 1 x + 1]
TESTS:
The input block must be a matrix:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.mix_column("mat")
...
TypeError: input block must be a 2 x 2 matrix over GF(16)
In addition, the dimensions of the input matrix must be  :
:
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 1, 2)
sage: mat = MS([[K("x^3 + x^2 + x + 1"), K("0")]])
sage: maes.mix_column(mat)
...
TypeError: input block must be a 2 x 2 matrix over GF(16)
Substitute a nibble (or a block of 4 bits) using the following S-box:
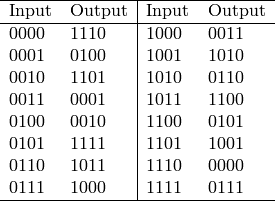
The values in the above S-box are taken from the first row of the first
S-box of the Data Encryption Standard (DES). Each nibble can be
thought of as an element of the finite field  of 16
elements. Thus in terms of
of 16
elements. Thus in terms of  , the S-box can also be
specified as:
, the S-box can also be
specified as:

Note that the above S-box is used for encryption. The S-box for decryption is obtained from the above S-box by reversing the role of the Input and Output columns. Thus the previous Input column for encryption now becomes the Output column for decryption, and the previous Output column for encryption is now the Input column for decryption. The S-box used for decryption can be specified as:

INPUT:
 matrix with entries over
matrix with entries over

OUTPUT:
 matrix resulting from applying an S-box on
entries of the
matrix resulting from applying an S-box on
entries of the  matrix block.
matrix block.EXAMPLES:
Here we work with elements of the finite field  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: mat = MS([[K("x^3 + x^2 + x + 1"), K("0")], [K("x^2 + x + 1"), K("x^3 + x")]])
sage: maes.nibble_sub(mat, algorithm="encrypt")
<BLANKLINE>
[ x^2 + x + 1 x^3 + x^2 + x]
[ x^3 x^2 + x]
But we can also work with binary strings:
sage: bin = BinaryStrings()
sage: B = bin.encoding("bi"); B
0110001001101001
sage: B = MS(maes.binary_to_GF(B)); B
<BLANKLINE>
[x^2 + x x]
[x^2 + x x^3 + 1]
sage: maes.nibble_sub(B, algorithm="encrypt")
<BLANKLINE>
[ x^3 + x + 1 x^3 + x^2 + 1]
[ x^3 + x + 1 x^3 + x]
sage: maes.nibble_sub(B, algorithm="decrypt")
<BLANKLINE>
[ x^3 + x x^2]
[ x^3 + x x^3 + x^2 + 1]
Here we work with integers  such that
such that 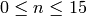 :
:
sage: P = [2, 6, 8, 14]; P
[2, 6, 8, 14]
sage: P = MS(maes.integer_to_GF(P)); P
<BLANKLINE>
[ x x^2 + x]
[ x^3 x^3 + x^2 + x]
sage: maes.nibble_sub(P, algorithm="encrypt")
<BLANKLINE>
[x^3 + x^2 + 1 x^3 + x + 1]
[ x + 1 0]
sage: maes.nibble_sub(P, algorithm="decrypt")
<BLANKLINE>
[ x^2 x^3 + x]
[x^2 + x + 1 0]
TESTS:
The input block must be a matrix:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.nibble_sub("mat")
...
TypeError: input block must be a 2 x 2 matrix over GF(16)
In addition, the dimensions of the input matrix must be  :
:
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 1, 2)
sage: mat = MS([[K("x^3 + x^2 + x + 1"), K("0")]])
sage: maes.nibble_sub(mat)
...
TypeError: input block must be a 2 x 2 matrix over GF(16)
The value for the option algorithm must be either the string "encrypt" or "decrypt":
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: mat = MS([[K("x^3 + x^2 + x + 1"), K("0")], [K("x^2 + x + 1"), K("x^3 + x")]])
sage: maes.nibble_sub(mat, algorithm="abc")
...
ValueError: the algorithm for nibble-sub must be either 'encrypt' or 'decrypt'
sage: maes.nibble_sub(mat, algorithm="e")
...
ValueError: the algorithm for nibble-sub must be either 'encrypt' or 'decrypt'
sage: maes.nibble_sub(mat, algorithm="d")
...
ValueError: the algorithm for nibble-sub must be either 'encrypt' or 'decrypt'
A random key within the key space of this Mini-AES block cipher. Like
the AES, Phan’s Mini-AES is a symmetric-key block cipher. A Mini-AES
key is a block of 16 bits, or a  matrix with entries over
the finite field
matrix with entries over
the finite field  . Thus the number of possible keys is
. Thus the number of possible keys is
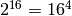 .
.
OUTPUT:
 matrix over the finite field
matrix over the finite field  , used
as a secret key for this Mini-AES block cipher.
, used
as a secret key for this Mini-AES block cipher.EXAMPLES:
Each nibble of a key is an element of the finite field
 :
:
sage: K = FiniteField(16, "x")
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: key = maes.random_key()
sage: [key[i][j] in K for i in xrange(key.nrows()) for j in xrange(key.ncols())]
[True, True, True, True]
Generate a random key, then perform encryption and decryption using that key:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: key = maes.random_key()
sage: P = MS.random_element()
sage: C = maes.encrypt(P, key)
sage: plaintxt = maes.decrypt(C, key)
sage: plaintxt == P
True
Return the round key for round n. Phan’s Mini-AES is defined to
have two rounds. The round key 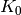 is generated and used prior to
the first round, with round keys
is generated and used prior to
the first round, with round keys 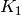 and
and 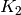 being used in rounds
1 and 2 respectively. In total, there are three round keys, each
generated from the secret key key.
being used in rounds
1 and 2 respectively. In total, there are three round keys, each
generated from the secret key key.
INPUT:
OUTPUT:
 -th round key.
-th round key.EXAMPLES:
Obtaining the round keys from the secret key:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: key = MS([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")], [K("x + 1"), K("0")] ])
sage: maes.round_key(key, 0)
<BLANKLINE>
[ x^3 + x^2 x^3 + x^2 + x + 1]
[ x + 1 0]
sage: key
<BLANKLINE>
[ x^3 + x^2 x^3 + x^2 + x + 1]
[ x + 1 0]
sage: maes.round_key(key, 1)
<BLANKLINE>
[ x + 1 x^3 + x^2 + x + 1]
[ 0 x^3 + x^2 + x + 1]
sage: maes.round_key(key, 2)
<BLANKLINE>
[x^2 + x x^3 + 1]
[x^2 + x x^2 + x]
TESTS:
Only two rounds are defined for this AES variant:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: key = MS([ [K("x^3 + x^2"), K("x^3 + x^2 + x + 1")], [K("x + 1"), K("0")] ])
sage: maes.round_key(key, -1)
...
ValueError: Mini-AES only defines two rounds
sage: maes.round_key(key, 3)
...
ValueError: Mini-AES only defines two rounds
The input key must be a matrix:
sage: maes.round_key("key", 0)
...
TypeError: secret key must be a 2 x 2 matrix over GF(16)
In addition, the dimensions of the key matrix must be  :
:
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 1, 2)
sage: key = MS([[K("x^3 + x^2 + x + 1"), K("0")]])
sage: maes.round_key(key, 2)
...
TypeError: secret key must be a 2 x 2 matrix over GF(16)
Return the S-box of Mini-AES.
EXAMPLES:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.sbox()
(14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7)
Rotate each row of block to the left by different nibble
amounts. The first or zero-th row is left unchanged, while the
second or row one is rotated left by one nibble. This has the effect
of only interchanging the nibbles in the second row. Let
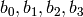 be four nibbles arranged as the following
be four nibbles arranged as the following
 matrix
matrix
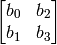
Then the operation of shift-row is the mapping
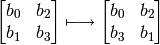
INPUT:
 matrix with entries over
matrix with entries over

OUTPUT:
 matrix resulting from applying shift-row on block.
matrix resulting from applying shift-row on block.EXAMPLES:
Here we work with elements of the finite field  :
:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 2, 2)
sage: mat = MS([[K("x^3 + x^2 + x + 1"), K("0")], [K("x^2 + x + 1"), K("x^3 + x")]])
sage: maes.shift_row(mat)
<BLANKLINE>
[x^3 + x^2 + x + 1 0]
[ x^3 + x x^2 + x + 1]
sage: mat
<BLANKLINE>
[x^3 + x^2 + x + 1 0]
[ x^2 + x + 1 x^3 + x]
But we can also work with binary strings:
sage: bin = BinaryStrings()
sage: B = bin.encoding("Qt"); B
0101000101110100
sage: B = MS(maes.binary_to_GF(B)); B
<BLANKLINE>
[ x^2 + 1 1]
[x^2 + x + 1 x^2]
sage: maes.shift_row(B)
<BLANKLINE>
[ x^2 + 1 1]
[ x^2 x^2 + x + 1]
Here we work with integers  such that
such that 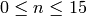 :
:
sage: P = [3, 6, 9, 12]; P
[3, 6, 9, 12]
sage: P = MS(maes.integer_to_GF(P)); P
<BLANKLINE>
[ x + 1 x^2 + x]
[ x^3 + 1 x^3 + x^2]
sage: maes.shift_row(P)
<BLANKLINE>
[ x + 1 x^2 + x]
[x^3 + x^2 x^3 + 1]
TESTS:
The input block must be a matrix:
sage: from sage.crypto.block_cipher.miniaes import MiniAES
sage: maes = MiniAES()
sage: maes.shift_row("block")
...
TypeError: input block must be a 2 x 2 matrix over GF(16)
In addition, the dimensions of the input matrix must be  :
:
sage: K = FiniteField(16, "x")
sage: MS = MatrixSpace(K, 1, 2)
sage: mat = MS([[K("x^3 + x^2 + x + 1"), K("0")]])
sage: maes.shift_row(mat)
...
TypeError: input block must be a 2 x 2 matrix over GF(16)