Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Cryptography »

A simplified variant of the Data Encryption Standard (DES). Note that Simplified DES or S-DES is for educational purposes only. It is a small-scale version of the DES designed to help beginners understand the basic structure of DES.
AUTHORS:
Bases: sage.structure.sage_object.SageObject
This class implements the Simplified Data Encryption Standard (S-DES) described in [Sch96]. Schaefer’s S-DES is for educational purposes only and is not secure for practical purposes. S-DES is a version of the DES with all parameters significantly reduced, but at the same time preserving the structure of DES. The goal of S-DES is to allow a beginner to understand the structure of DES, thus laying a foundation for a thorough study of DES. Its goal is as a teaching tool in the same spirit as Phan’s Mini-AES [Pha02].
EXAMPLES:
Encrypt a random block of 8-bit plaintext using a random key, decrypt the ciphertext, and compare the result with the original plaintext:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES(); sdes
Simplified DES block cipher with 10-bit keys
sage: bin = BinaryStrings()
sage: P = [bin(str(randint(0, 1))) for i in xrange(8)]
sage: K = sdes.random_key()
sage: C = sdes.encrypt(P, K)
sage: plaintxt = sdes.decrypt(C, K)
sage: plaintxt == P
True
We can also encrypt binary strings that are larger than 8 bits in length. However, the number of bits in that binary string must be positive and a multiple of 8:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: bin = BinaryStrings()
sage: P = bin.encoding("Encrypt this using S-DES!")
sage: Mod(len(P), 8) == 0
True
sage: K = sdes.list_to_string(sdes.random_key())
sage: C = sdes(P, K, algorithm="encrypt")
sage: plaintxt = sdes(C, K, algorithm="decrypt")
sage: plaintxt == P
True
REFERENCES:
| [Pha02] | R. C.-W. Phan. Mini advanced encryption standard (mini-AES): a testbed for cryptanalysis students. Cryptologia, 26(4):283–306, 2002. |
| [Sch96] | E. Schaefer. A simplified data encryption algorithm. Cryptologia, 20(1):77–84, 1996. |
Return the block length of Schaefer’s S-DES block cipher. A key in Schaefer’s S-DES is a block of 10 bits.
OUTPUT:
EXAMPLES:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.block_length()
10
Return an 8-bit plaintext corresponding to the ciphertext C,
using S-DES decryption with key K. The decryption process of
S-DES is as follows. Let  be the initial permutation function,
be the initial permutation function,
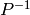 the corresponding inverse permutation,
the corresponding inverse permutation, 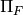 the
permutation/substitution function, and
the
permutation/substitution function, and 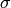 the switch function.
The ciphertext block C first goes through
the switch function.
The ciphertext block C first goes through  , the output of
which goes through
, the output of
which goes through 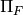 using the second subkey. Then we apply
the switch function to the output of the last function, and the
result is then fed into
using the second subkey. Then we apply
the switch function to the output of the last function, and the
result is then fed into 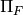 using the first subkey. Finally,
run the output through
using the first subkey. Finally,
run the output through 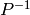 to get the plaintext.
to get the plaintext.
INPUT:
OUTPUT:
The 8-bit plaintext corresponding to C, obtained using the key K.
EXAMPLES:
Decrypt an 8-bit ciphertext block:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: C = [0, 1, 0, 1, 0, 1, 0, 1]
sage: K = [1, 0, 1, 0, 0, 0, 0, 0, 1, 0]
sage: sdes.decrypt(C, K)
[0, 0, 0, 1, 0, 1, 0, 1]
We can also work with strings of bits:
sage: C = "01010101"
sage: K = "1010000010"
sage: sdes.decrypt(sdes.string_to_list(C), sdes.string_to_list(K))
[0, 0, 0, 1, 0, 1, 0, 1]
TESTS:
The ciphertext must be a block of 8 bits:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.decrypt("C", "K")
...
TypeError: ciphertext must be a list of 8 bits
sage: sdes.decrypt([], "K")
...
ValueError: ciphertext must be a list of 8 bits
sage: sdes.decrypt([1, 2, 3, 4], "K")
...
ValueError: ciphertext must be a list of 8 bits
The key must be a block of 10 bits:
sage: sdes.decrypt([1, 0, 1, 0, 1, 1, 0, 1], "K")
...
TypeError: the key must be a list of 10 bits
sage: sdes.decrypt([1, 0, 1, 0, 1, 1, 0, 1], [])
...
TypeError: the key must be a list of 10 bits
sage: sdes.decrypt([1, 0, 1, 0, 1, 1, 0, 1], [1, 2, 3, 4, 5])
...
TypeError: the key must be a list of 10 bits
The value of each element of C or K must be either 0 or 1:
sage: C = [1, 2, 3, 4, 5, 6, 7, 8]
sage: K = [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
sage: sdes.decrypt(C, K)
...
TypeError: Argument x (= 2) is not a valid string.
sage: C = [0, 1, 0, 0, 1, 1, 1, 0]
sage: K = [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
sage: sdes.decrypt(C, K)
...
TypeError: Argument x (= 13) is not a valid string.
Return an 8-bit ciphertext corresponding to the plaintext P,
using S-DES encryption with key K. The encryption process of
S-DES is as follows. Let  be the initial permutation function,
be the initial permutation function,
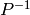 the corresponding inverse permutation,
the corresponding inverse permutation, 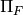 the
permutation/substitution function, and
the
permutation/substitution function, and 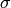 the switch function.
The plaintext block P first goes through
the switch function.
The plaintext block P first goes through  , the output of
which goes through
, the output of
which goes through 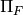 using the first subkey. Then we apply
the switch function to the output of the last function, and the
result is then fed into
using the first subkey. Then we apply
the switch function to the output of the last function, and the
result is then fed into 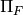 using the second subkey. Finally,
run the output through
using the second subkey. Finally,
run the output through 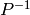 to get the ciphertext.
to get the ciphertext.
INPUT:
OUTPUT:
The 8-bit ciphertext corresponding to P, obtained using the key K.
EXAMPLES:
Encrypt an 8-bit plaintext block:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: P = [0, 1, 0, 1, 0, 1, 0, 1]
sage: K = [1, 0, 1, 0, 0, 0, 0, 0, 1, 0]
sage: sdes.encrypt(P, K)
[1, 1, 0, 0, 0, 0, 0, 1]
We can also work with strings of bits:
sage: P = "01010101"
sage: K = "1010000010"
sage: sdes.encrypt(sdes.string_to_list(P), sdes.string_to_list(K))
[1, 1, 0, 0, 0, 0, 0, 1]
TESTS:
The plaintext must be a block of 8 bits:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.encrypt("P", "K")
...
TypeError: plaintext must be a list of 8 bits
sage: sdes.encrypt([], "K")
...
ValueError: plaintext must be a list of 8 bits
sage: sdes.encrypt([1, 2, 3, 4], "K")
...
ValueError: plaintext must be a list of 8 bits
The key must be a block of 10 bits:
sage: sdes.encrypt([1, 0, 1, 0, 1, 1, 0, 1], "K")
...
TypeError: the key must be a list of 10 bits
sage: sdes.encrypt([1, 0, 1, 0, 1, 1, 0, 1], [])
...
TypeError: the key must be a list of 10 bits
sage: sdes.encrypt([1, 0, 1, 0, 1, 1, 0, 1], [1, 2, 3, 4, 5])
...
TypeError: the key must be a list of 10 bits
The value of each element of P or K must be either 0 or 1:
sage: P = [1, 2, 3, 4, 5, 6, 7, 8]
sage: K = [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
sage: sdes.encrypt(P, K)
...
TypeError: Argument x (= 2) is not a valid string.
sage: P = [0, 1, 0, 0, 1, 1, 1, 0]
sage: K = [11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
sage: sdes.encrypt(P, K)
...
TypeError: Argument x (= 13) is not a valid string.
Return the initial permutation of B. Denote the initial
permutation function by  and let
and let 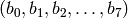 be a vector of 8 bits, where each
be a vector of 8 bits, where each 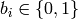 . Then
. Then
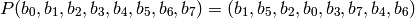
The inverse permutation is 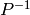 :
:
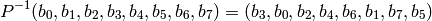
INPUT:
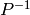 ; if False then use the initial
permutation
; if False then use the initial
permutation 
OUTPUT:
The initial permutation of B if inverse=False, or the inverse permutation of B if inverse=True.
EXAMPLES:
The initial permutation of a list of 8 bits:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: B = [1, 0, 1, 1, 0, 1, 0, 0]
sage: P = sdes.initial_permutation(B); P
[0, 1, 1, 1, 1, 0, 0, 0]
Recovering the original list of 8 bits from the permutation:
sage: Pinv = sdes.initial_permutation(P, inverse=True)
sage: Pinv; B
[1, 0, 1, 1, 0, 1, 0, 0]
[1, 0, 1, 1, 0, 1, 0, 0]
We can also work with a string of bits:
sage: S = "10110100"
sage: L = sdes.string_to_list(S)
sage: P = sdes.initial_permutation(L); P
[0, 1, 1, 1, 1, 0, 0, 0]
sage: sdes.initial_permutation(sdes.string_to_list("01111000"), inverse=True)
[1, 0, 1, 1, 0, 1, 0, 0]
TESTS:
The input block must be a list:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.initial_permutation("B")
...
TypeError: input block must be a list of 8 bits
sage: sdes.initial_permutation(())
...
TypeError: input block must be a list of 8 bits
The input block must be a list of 8 bits:
sage: sdes.initial_permutation([])
...
ValueError: input block must be a list of 8 bits
sage: sdes.initial_permutation([1, 2, 3, 4, 5, 6, 7, 8, 9])
...
ValueError: input block must be a list of 8 bits
The value of each element of the list must be either 0 or 1:
sage: sdes.initial_permutation([1, 2, 3, 4, 5, 6, 7, 8])
...
TypeError: Argument x (= 2) is not a valid string.
Return a circular left shift of B by n positions. Let
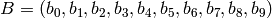 be a vector
of 10 bits. Then the left shift operation
be a vector
of 10 bits. Then the left shift operation 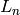 is performed on the
first 5 bits and the last 5 bits of
is performed on the
first 5 bits and the last 5 bits of  separately. That is, if the
number of shift positions is n=1, then
separately. That is, if the
number of shift positions is n=1, then 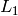 is defined as
is defined as
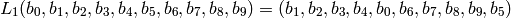
If the number of shift positions is n=2, then 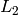 is given by
is given by
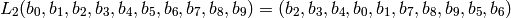
INPUT:
OUTPUT:
The circular left shift of each half of B.
EXAMPLES:
Circular left shift by 1 position of a 10-bit string:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: B = [1, 0, 0, 0, 0, 0, 1, 1, 0, 0]
sage: sdes.left_shift(B)
[0, 0, 0, 0, 1, 1, 1, 0, 0, 0]
sage: sdes.left_shift([1, 0, 1, 0, 0, 0, 0, 0, 1, 0])
[0, 1, 0, 0, 1, 0, 0, 1, 0, 0]
Circular left shift by 2 positions of a 10-bit string:
sage: B = [0, 0, 0, 0, 1, 1, 1, 0, 0, 0]
sage: sdes.left_shift(B, n=2)
[0, 0, 1, 0, 0, 0, 0, 0, 1, 1]
Here we work with a string of bits:
sage: S = "1000001100"
sage: L = sdes.string_to_list(S)
sage: sdes.left_shift(L)
[0, 0, 0, 0, 1, 1, 1, 0, 0, 0]
sage: sdes.left_shift(sdes.string_to_list("1010000010"), n=2)
[1, 0, 0, 1, 0, 0, 1, 0, 0, 0]
TESTS:
The input block must be a list:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.left_shift("B")
...
TypeError: input block must be a list of 10 bits
sage: sdes.left_shift(())
...
TypeError: input block must be a list of 10 bits
The input block must be a list of 10 bits:
sage: sdes.left_shift([])
...
ValueError: input block must be a list of 10 bits
sage: sdes.left_shift([1, 2, 3, 4, 5])
...
ValueError: input block must be a list of 10 bits
The value of each element of the list must be either 0 or 1:
sage: sdes.left_shift([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
...
TypeError: Argument x (= 2) is not a valid string.
The number of shift positions must be either 1 or 2:
sage: B = [0, 0, 0, 0, 1, 1, 1, 0, 0, 0]
sage: sdes.left_shift(B, n=-1)
...
ValueError: input n must be either 1 or 2
sage: sdes.left_shift(B, n=3)
...
ValueError: input n must be either 1 or 2
Return a binary string representation of the list B.
INPUT:
OUTPUT:
The binary string representation of B.
EXAMPLES:
A binary string representation of a list of bits:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: L = [0, 0, 0, 0, 1, 1, 0, 1, 0, 0]
sage: sdes.list_to_string(L)
0000110100
TESTS:
Input B must be a non-empty list:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.list_to_string("L")
...
TypeError: input B must be a non-empty list of bits
sage: sdes.list_to_string([])
...
ValueError: input B must be a non-empty list of bits
Input must be a non-empty list of bits:
sage: sdes.list_to_string([0, 1, 2])
...
IndexError: tuple index out of range
Return a permutation of a 10-bit string. This permutation is called
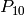 and is specified as follows. Let
and is specified as follows. Let
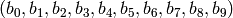 be a vector of
10 bits where each
be a vector of
10 bits where each 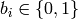 . Then
. Then 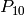 is given by
is given by
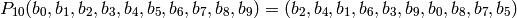
INPUT:
OUTPUT:
A permutation of B.
EXAMPLES:
Permute a 10-bit string:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: B = [1, 1, 0, 0, 1, 0, 0, 1, 0, 1]
sage: sdes.permutation10(B)
[0, 1, 1, 0, 0, 1, 1, 0, 1, 0]
sage: sdes.permutation10([0, 1, 1, 0, 1, 0, 0, 1, 0, 1])
[1, 1, 1, 0, 0, 1, 0, 0, 1, 0]
sage: sdes.permutation10([1, 0, 1, 0, 0, 0, 0, 0, 1, 0])
[1, 0, 0, 0, 0, 0, 1, 1, 0, 0]
Here we work with a string of bits:
sage: S = "1100100101"
sage: L = sdes.string_to_list(S)
sage: sdes.permutation10(L)
[0, 1, 1, 0, 0, 1, 1, 0, 1, 0]
sage: sdes.permutation10(sdes.string_to_list("0110100101"))
[1, 1, 1, 0, 0, 1, 0, 0, 1, 0]
TESTS:
The input block must be a list:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.permutation10("B")
...
TypeError: input block must be a list of 10 bits
sage: sdes.permutation10(())
...
TypeError: input block must be a list of 10 bits
The input block must be a list of 10 bits:
sage: sdes.permutation10([])
...
ValueError: input block must be a list of 10 bits
sage: sdes.permutation10([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
...
ValueError: input block must be a list of 10 bits
The value of each element of the list must be either 0 or 1:
sage: sdes.permutation10([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
...
TypeError: Argument x (= 3) is not a valid string.
Return a permutation of a 4-bit string. This permutation is called
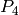 and is specified as follows. Let
and is specified as follows. Let
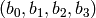 be a vector of 4 bits where each
be a vector of 4 bits where each
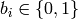 . Then
. Then 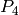 is defined by
is defined by
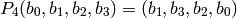
INPUT:
OUTPUT:
A permutation of B.
EXAMPLES:
Permute a 4-bit string:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: B = [1, 1, 0, 0]
sage: sdes.permutation4(B)
[1, 0, 0, 1]
sage: sdes.permutation4([0, 1, 0, 1])
[1, 1, 0, 0]
We can also work with a string of bits:
sage: S = "1100"
sage: L = sdes.string_to_list(S)
sage: sdes.permutation4(L)
[1, 0, 0, 1]
sage: sdes.permutation4(sdes.string_to_list("0101"))
[1, 1, 0, 0]
TESTS:
The input block must be a list:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.permutation4("B")
...
TypeError: input block must be a list of 4 bits
sage: sdes.permutation4(())
...
TypeError: input block must be a list of 4 bits
The input block must be a list of 4 bits:
sage: sdes.permutation4([])
...
ValueError: input block must be a list of 4 bits
sage: sdes.permutation4([1, 2, 3, 4, 5])
...
ValueError: input block must be a list of 4 bits
The value of each element of the list must be either 0 or 1:
sage: sdes.permutation4([1, 2, 3, 4])
...
TypeError: Argument x (= 2) is not a valid string.
Return a permutation of an 8-bit string. This permutation is called
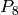 and is specified as follows. Let
and is specified as follows. Let
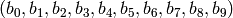 be a vector of
10 bits where each
be a vector of
10 bits where each 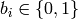 . Then
. Then 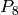 picks out 8 of
those 10 bits and permutes those 8 bits:
picks out 8 of
those 10 bits and permutes those 8 bits:
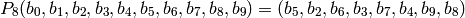
INPUT:
OUTPUT:
Pick out 8 of the 10 bits of B and permute those 8 bits.
EXAMPLES:
Permute a 10-bit string:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: B = [1, 1, 0, 0, 1, 0, 0, 1, 0, 1]
sage: sdes.permutation8(B)
[0, 0, 0, 0, 1, 1, 1, 0]
sage: sdes.permutation8([0, 1, 1, 0, 1, 0, 0, 1, 0, 1])
[0, 1, 0, 0, 1, 1, 1, 0]
sage: sdes.permutation8([0, 0, 0, 0, 1, 1, 1, 0, 0, 0])
[1, 0, 1, 0, 0, 1, 0, 0]
We can also work with a string of bits:
sage: S = "1100100101"
sage: L = sdes.string_to_list(S)
sage: sdes.permutation8(L)
[0, 0, 0, 0, 1, 1, 1, 0]
sage: sdes.permutation8(sdes.string_to_list("0110100101"))
[0, 1, 0, 0, 1, 1, 1, 0]
TESTS:
The input block must be a list:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.permutation8("B")
...
TypeError: input block must be a list of 10 bits
sage: sdes.permutation8(())
...
TypeError: input block must be a list of 10 bits
The input block must be a list of 10 bits:
sage: sdes.permutation8([])
...
ValueError: input block must be a list of 10 bits
sage: sdes.permutation8([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
...
ValueError: input block must be a list of 10 bits
The value of each element of the list must be either 0 or 1:
sage: sdes.permutation8([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
...
TypeError: Argument x (= 6) is not a valid string.
Apply the function 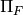 on the block B using subkey key.
Let
on the block B using subkey key.
Let 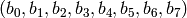 be a vector of 8 bits where each
be a vector of 8 bits where each 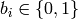 , let
, let  and
and
 be the leftmost 4 bits and rightmost 4 bits of B
respectively, and let
be the leftmost 4 bits and rightmost 4 bits of B
respectively, and let 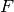 be a function mapping 4-bit strings to
4-bit strings. Then
be a function mapping 4-bit strings to
4-bit strings. Then
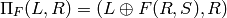
where  is a subkey and
is a subkey and 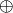 denotes the bit-wise
exclusive-OR function.
denotes the bit-wise
exclusive-OR function.
The function 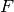 can be described as follows. Its 4-bit input block
can be described as follows. Its 4-bit input block
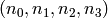 is first expanded into an 8-bit block
to become
is first expanded into an 8-bit block
to become 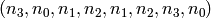 . This is
usually represented as follows
. This is
usually represented as follows
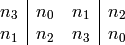
Let 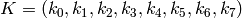 be an 8-bit
subkey. Then
be an 8-bit
subkey. Then  is added to the above expanded input block using
exclusive-OR to produce
is added to the above expanded input block using
exclusive-OR to produce
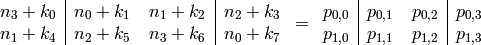
Now read the first row as the 4-bit string
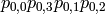 and input this 4-bit string through
S-box
and input this 4-bit string through
S-box 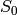 to get a 2-bit output.
to get a 2-bit output.
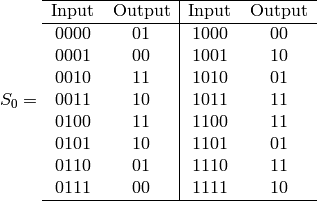
Next read the second row as the 4-bit string
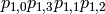 and input this 4-bit string through
S-box
and input this 4-bit string through
S-box 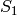 to get another 2-bit output.
to get another 2-bit output.
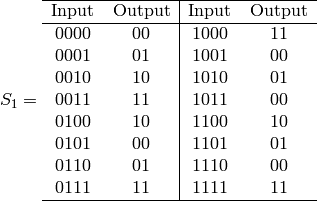
Denote the 4 bits produced by 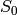 and
and 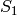 as
as 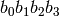 .
This 4-bit string undergoes another permutation called
.
This 4-bit string undergoes another permutation called 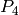 as
follows:
as
follows:
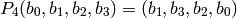
The output of 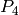 is the output of the function
is the output of the function 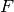 .
.
INPUT:
OUTPUT:
The result of applying the function 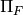 to B.
to B.
EXAMPLES:
Applying the function 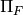 to an 8-bit block and an 8-bit subkey:
to an 8-bit block and an 8-bit subkey:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: B = [1, 0, 1, 1, 1, 1, 0, 1]
sage: K = [1, 1, 0, 1, 0, 1, 0, 1]
sage: sdes.permute_substitute(B, K)
[1, 0, 1, 0, 1, 1, 0, 1]
We can also work with strings of bits:
sage: B = "10111101"
sage: K = "11010101"
sage: B = sdes.string_to_list(B); K = sdes.string_to_list(K)
sage: sdes.permute_substitute(B, K)
[1, 0, 1, 0, 1, 1, 0, 1]
TESTS:
The input B must be a block of 8 bits:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.permute_substitute("B", "K")
...
TypeError: input B must be an 8-bit string
sage: sdes.permute_substitute([], "K")
...
ValueError: input B must be an 8-bit string
The input key must be an 8-bit subkey:
sage: sdes.permute_substitute([0, 1, 0, 0, 1, 1, 1, 0], "K")
...
TypeError: input key must be an 8-bit subkey
sage: sdes.permute_substitute([0, 1, 0, 0, 1, 1, 1, 0], [])
...
ValueError: input key must be an 8-bit subkey
The value of each element of B or key must be either 0 or 1:
sage: B = [1, 2, 3, 4, 5, 6, 7, 8]
sage: K = [0, 1, 2, 3, 4, 5, 6, 7]
sage: sdes.permute_substitute(B, K)
...
TypeError: Argument x (= 2) is not a valid string.
sage: B = [0, 1, 0, 0, 1, 1, 1, 0]
sage: K = [1, 2, 3, 4, 5, 6, 7, 8]
sage: sdes.permute_substitute(B, K)
...
TypeError: Argument x (= 2) is not a valid string.
Return a random 10-bit key.
EXAMPLES:
The size of each key is the same as the block size:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: key = sdes.random_key()
sage: len(key) == sdes.block_length()
True
Return the S-boxes of simplified DES.
EXAMPLES:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sbox = sdes.sbox()
sage: sbox[0]; sbox[1]
(1, 0, 3, 2, 3, 2, 1, 0, 0, 2, 1, 3, 3, 1, 3, 2)
(0, 1, 2, 3, 2, 0, 1, 3, 3, 0, 1, 0, 2, 1, 0, 3)
Return a list representation of the binary string S.
INPUT:
OUTPUT:
A list representation of the string S.
EXAMPLES:
A list representation of a string of bits:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: S = "0101010110"
sage: sdes.string_to_list(S)
[0, 1, 0, 1, 0, 1, 0, 1, 1, 0]
TESTS:
Input must be a non-empty string:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.string_to_list("")
...
ValueError: input S must be a non-empty string of bits
sage: sdes.string_to_list(1)
...
TypeError: input S must be a non-empty string of bits
Input must be a non-empty string of bits:
sage: sdes.string_to_list("0123")
...
TypeError: Argument x (= 2) is not a valid string.
Return the n-th subkey based on the key K.
INPUT:
OUTPUT:
The n-th subkey based on the secret key K.
EXAMPLES:
Obtain the first subkey from a secret key:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: key = [1, 0, 1, 0, 0, 0, 0, 0, 1, 0]
sage: sdes.subkey(key, n=1)
[1, 0, 1, 0, 0, 1, 0, 0]
Obtain the second subkey from a secret key:
sage: key = [1, 0, 1, 0, 0, 0, 0, 0, 1, 0]
sage: sdes.subkey(key, n=2)
[0, 1, 0, 0, 0, 0, 1, 1]
We can also work with strings of bits:
sage: K = "1010010010"
sage: L = sdes.string_to_list(K)
sage: sdes.subkey(L, n=1)
[1, 0, 1, 0, 0, 1, 0, 1]
sage: sdes.subkey(sdes.string_to_list("0010010011"), n=2)
[0, 1, 1, 0, 1, 0, 1, 0]
TESTS:
Input K must be a 10-bit key:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.subkey("K")
...
TypeError: input K must be a 10-bit key
sage: sdes.subkey([])
...
ValueError: input K must be a 10-bit key
There are only two subkeys:
sage: key = [1, 0, 1, 0, 0, 0, 0, 0, 1, 0]
sage: sdes.subkey(key, n=0)
...
ValueError: input n must be either 1 or 2
sage: sdes.subkey(key, n=3)
...
ValueError: input n must be either 1 or 2
Interchange the first 4 bits with the last 4 bits in the list B
of 8 bits. Let 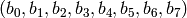 be a vector of 8 bits, where each
be a vector of 8 bits, where each 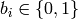 . Then the
switch function
. Then the
switch function 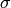 is given by
is given by
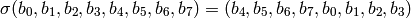
INPUT:
OUTPUT:
A block of the same dimension, but in which the first 4 bits from B has been switched for the last 4 bits in B.
EXAMPLES:
Interchange the first 4 bits with the last 4 bits:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: B = [1, 1, 1, 0, 1, 0, 0, 0]
sage: sdes.switch(B)
[1, 0, 0, 0, 1, 1, 1, 0]
sage: sdes.switch([1, 1, 1, 1, 0, 0, 0, 0])
[0, 0, 0, 0, 1, 1, 1, 1]
We can also work with a string of bits:
sage: S = "11101000"
sage: L = sdes.string_to_list(S)
sage: sdes.switch(L)
[1, 0, 0, 0, 1, 1, 1, 0]
sage: sdes.switch(sdes.string_to_list("11110000"))
[0, 0, 0, 0, 1, 1, 1, 1]
TESTS:
The input block must be a list:
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: sdes.switch("B")
...
TypeError: input block must be a list of 8 bits
sage: sdes.switch(())
...
TypeError: input block must be a list of 8 bits
The input block must be a list of 8 bits:
sage: sdes.switch([])
...
ValueError: input block must be a list of 8 bits
sage: sdes.switch([1, 2, 3, 4, 5, 6, 7, 8, 9])
...
ValueError: input block must be a list of 8 bits
The value of each element of the list must be either 0 or 1:
sage: sdes.switch([1, 2, 3, 4, 5, 6, 7, 8])
...
TypeError: Argument x (= 5) is not a valid string.