Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Cryptography »

Sage supports polynomial system generation for small scale (and full
scale) AES variants over 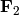 and
and 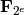 . Also, Sage supports
both the specification of SR as given in the papers [CMR05] and
[CMR06] and a variant of SR* which is equivalent to AES.
. Also, Sage supports
both the specification of SR as given in the papers [CMR05] and
[CMR06] and a variant of SR* which is equivalent to AES.
SR is a family of parameterizable variants of the AES suitable as a framework for comparing different cryptanalytic techniques that can be brought to bear on the AES. It is different from Mini-AES, whose purpose is as a teaching tool to help beginners understand the basic structure and working of the full AES.
AUTHORS:
EXAMPLES:
We construct SR(1,1,1,4) and study its properties.
sage: sr = mq.SR(1, 1, 1, 4)
n is the number of rounds, r the number of rows in the state array, c the number of columns in the state array, and e the degree of the underlying field.
sage: sr.n, sr.r, sr.c, sr.e
(1, 1, 1, 4)
By default variables are ordered reverse to as they appear, e.g.:
sage: print sr.R.repr_long()
Polynomial Ring
Base Ring : Finite Field in a of size 2^4
Size : 20 Variables
Block 0 : Ordering : degrevlex
Names : k100, k101, k102, k103, x100, x101, x102, x103, w100, w101, w102, w103, s000, s001, s002, s003, k000, k001, k002, k003
However, this can be prevented by passing in reverse_variables=False to the constructor.
For SR(1, 1, 1, 4) the ShiftRows matrix isn’t that interesting.:
sage: sr.ShiftRows
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
Also, the MixColumns matrix is the identity matrix.:
sage: sr.MixColumns
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
Lin, however, is not the identity matrix.:
sage: sr.Lin
[ a^2 + 1 1 a^3 + a^2 a^2 + 1]
[ a a 1 a^3 + a^2 + a + 1]
[ a^3 + a a^2 a^2 1]
[ 1 a^3 a + 1 a + 1]
M and Mstar are identical for SR(1, 1, 1, 4):
sage: sr.M
[ a^2 + 1 1 a^3 + a^2 a^2 + 1]
[ a a 1 a^3 + a^2 + a + 1]
[ a^3 + a a^2 a^2 1]
[ 1 a^3 a + 1 a + 1]
sage: sr.Mstar
[ a^2 + 1 1 a^3 + a^2 a^2 + 1]
[ a a 1 a^3 + a^2 + a + 1]
[ a^3 + a a^2 a^2 1]
[ 1 a^3 a + 1 a + 1]
We can compute a Groebner basis for the ideals spanned by SR instances to recover all solutions to the system.:
sage: sr = mq.SR(1,1,1,4, gf2=True, polybori=True)
sage: K = sr.base_ring()
sage: a = K.gen()
sage: K = [a]
sage: P = [1]
sage: F,s = sr.polynomial_system(P=P, K=K)
sage: F.groebner_basis()
[k100, k101 + 1, k102, k103 + k003,
x100 + 1, x101 + k003 + 1, x102 + k003 + 1,
x103 + k003, w100, w101, w102 + 1, w103 + k003 + 1,
s000 + 1, s001 + k003, s002 + k003, s003 + k003 + 1,
k000, k001, k002 + 1]
Note that the order of k000, k001, k002 and k003 is
little endian. Thus the result k002 + 1, k001, k000 indicates that
the key is either  or
or 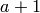 . We can verify that both keys encrypt P
to the same ciphertext:
. We can verify that both keys encrypt P
to the same ciphertext:
sage: sr(P,[a])
[0]
sage: sr(P,[a+1])
[0]
All solutions can easily be recovered using the variety function for ideals.:
sage: I = F.ideal()
sage: for V in I.variety():
... for k,v in sorted(V.iteritems()):
... print k,v
... print
k003 0
k002 1
k001 0
k000 0
s003 1
s002 0
s001 0
s000 1
w103 1
w102 1
w101 0
w100 0
x103 0
x102 1
x101 1
x100 1
k103 0
k102 0
k101 1
k100 0
<BLANKLINE>
k003 1
k002 1
k001 0
k000 0
s003 0
s002 1
s001 1
s000 1
w103 0
w102 1
w101 0
w100 0
x103 1
x102 0
x101 0
x100 1
k103 1
k102 0
k101 1
k100 0
We can also verify the correctness of the variety by evaluating all ideal generators on all points.:
sage: for V in I.variety():
... for f in I.gens():
... if f.subs(V) != 0:
... print "epic fail"
Note that the S-Box object for SR can be constructed with a call to sr.sbox():
sage: sr = mq.SR(1,1,1,4, gf2=True, polybori=True)
sage: S = sr.sbox()
For example, we can now study the difference distribution matrix of S:
sage: S.difference_distribution_matrix()
[16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 2 2 2 2 0 0 0 2 0 0 0 2 4 0 0]
[ 0 2 0 4 2 2 2 0 0 2 0 0 0 0 0 2]
[ 0 2 4 0 0 2 0 0 2 2 0 2 0 0 2 0]
[ 0 0 2 0 4 2 0 0 0 0 2 0 2 0 2 2]
[ 0 0 0 2 0 0 0 2 4 2 0 0 2 0 2 2]
[ 0 4 0 0 0 2 0 2 0 2 2 0 2 2 0 0]
[ 0 2 0 0 0 0 2 0 0 0 0 2 4 2 2 2]
[ 0 2 2 0 0 0 2 2 2 0 2 0 0 0 0 4]
[ 0 0 2 2 0 0 0 0 0 2 2 4 0 2 0 2]
[ 0 0 2 0 2 0 2 2 0 4 0 2 2 0 0 0]
[ 0 0 0 0 2 0 2 0 2 2 4 0 0 2 2 0]
[ 0 0 0 2 0 4 2 0 2 0 2 2 2 0 0 0]
[ 0 0 0 0 2 2 0 4 2 0 0 2 0 2 0 2]
[ 0 0 2 2 0 2 4 2 0 0 0 0 0 2 2 0]
[ 0 2 0 2 2 0 0 2 0 0 2 2 0 0 4 0]
or use S to find alternative polynomial representations for the S-Box.:
sage: S.polynomials(degree=3)
[x0*x1 + x1*x2 + x0*x3 + x0*y2 + x1 + y0 + y1 + 1,
x0*x1 + x0*x2 + x0*y0 + x0*y1 + x0*y2 + x1 + x2 + y0 + y1 + y2,
x0*x1 + x0*x2 + x0*x3 + x1*x3 + x0*y0 + x1*y0 + x0*y1 + x0*y3,
x0*x1 + x0*x2 + x0*x3 + x1*x3 + x0*y0 + x1*y1 + x0*y3 + x1 + y0 + y1 + 1,
x0*x1 + x0*x2 + x0*y2 + x1*y2 + x0*y3 + x0 + x1,
x0*x3 + x1*x3 + x0*y1 + x0*y2 + x1*y3 + x0 + x1 + x2 + x3 + y0 + y1 + y3 + 1,
x0*x1 + x1*x3 + x2*x3 + x0*y0 + x0*y2 + x0*y3 + x2 + y0 + y3,
x0*x1 + x0*x2 + x0*x3 + x1*x3 + x2*y0 + x0*y2 + x0 + x2 + x3 + y3,
x0*x3 + x1*x3 + x0*y0 + x2*y1 + x0*y2 + x3 + y3,
x0*x1 + x0*x2 + x0*y0 + x0*y1 + x2*y2 + x0*y3 + x1 + y0 + y1 + 1,
x0*x3 + x1*x3 + x0*y0 + x0*y1 + x0*y3 + x2*y3 + y0 + y3,
x0*x1 + x0*x2 + x3*y0 + x0*y1 + x0*y3 + y0,
x0*y0 + x0*y1 + x3*y1 + x0 + x2 + y0 + y3,
x0*y0 + x3*y2 + y0,
x0*x1 + x0*x2 + x0*x3 + x1*x3 + x0*y0 + x0*y2 + x3*y3 + y0,
x0*x2 + x0*x3 + x0*y1 + y0*y1 + x0*y3 + x2 + x3 + y3,
x0*x2 + x0*y0 + y0*y2 + x0*y3 + x0 + y0,
x0*x1 + x0*x2 + x1*x3 + x0*y2 + y0*y3 + y0,
x0*x1 + x0*y0 + y1*y2 + x0*y3 + x1 + x2 + y0 + 1,
x0*x2 + x1*x3 + x0*y1 + x0*y2 + x0*y3 + y1*y3 + x0 + y0 + y3,
x0*x1 + x0*x2 + x0*x3 + x0*y1 + x0*y2 + x0*y3 + y2*y3 + x0 + x1 + x2 + x3 + y1 + y3 + 1,
x0*x1*x2 + x0*x3 + x0*y0 + x0*y1 + x0*y2 + x0,
x0*x1*x3 + x0*x2 + x0*x3 + x0*y1 + x0*y3 + x0,
x0*x1*y0 + x0*x1 + x0*y0 + x0,
x0*x1*y1,
x0*x1*y2 + x0*x2 + x0*y2 + x0*y3 + x0,
x0*x1*y3 + x0*x1 + x0*x3 + x0*y0 + x0*y1 + x0*y2 + x0,
x0*x2*x3 + x0*x1 + x0*x3 + x0*y1 + x0*y2 + x0*y3 + x0,
x0*x2*y0 + x0*x1 + x0*x2 + x0*x3 + x0*y1 + x0*y2,
x0*x2*y1 + x0*x2 + x0*x3 + x0*y0 + x0*y1 + x0*y2 + x0,
x0*x2*y2 + x0*x2 + x0*y3 + x0,
x0*x2*y3 + x0*x2 + x0*y3 + x0,
x0*x3*y0 + x0*x1 + x0*x2 + x0*y0 + x0*y1 + x0*y3,
x0*x3*y1 + x0*x2 + x0*y1 + x0*y3 + x0,
x0*x3*y2,
x0*x3*y3 + x0*x1 + x0*y1 + x0*y2 + x0*y3 + x0,
x0*y0*y1 + x0*y1,
x0*y0*y2 + x0*x2 + x0*y3 + x0,
x0*y0*y3 + x0*x1 + x0*x3 + x0*y0 + x0*y1 + x0*y2 + x0*y3 + x0,
x0*y1*y2 + x0*x2 + x0*y3 + x0,
x0*y1*y3 + x0*x3 + x0*y0 + x0*y2 + x0*y3,
x0*y2*y3 + x0*y2,
x1*x2*x3 + x0*x1 + x1*x3 + x0*y0 + x0*y1 + x2 + x3 + y3,
x1*x2*y0 + x0*x1 + x1*x3 + x0*y0 + x0*y1 + x2 + x3 + y3,
x1*x2*y1 + x0*x1 + x1*x3 + x0*y0 + x1 + x2 + x3 + y0 + y1 + y3 + 1,
x1*x2*y2 + x0*x1 + x0*y0 + x0*y1 + x0 + x1 + y0 + y1 + 1,
x1*x2*y3 + x0*x1 + x1*x3 + x0*y0 + x1 + x2 + x3 + y0 + y1 + y3 + 1,
x1*x3*y0 + x0*x1 + x0*x2 + x0*x3 + x1*x3 + x0*y0 + x0*y1 + x0*y3,
x1*x3*y1 + x0*x2 + x0*x3 + x0*y3 + x2 + x3 + y3,
x1*x3*y2 + x0*x2 + x0*x3 + x1*x3 + x0*y1 + x0*y3 + x0,
x1*x3*y3 + x0*x1 + x0*x2 + x0*x3 + x0*y0 + x0*y1 + x0*y3,
x1*y0*y1 + x0*x2 + x0*x3 + x0*y3 + x2 + x3 + y3,
x1*y0*y2 + x0*x2 + x0*x3 + x1*x3 + x0*y1 + x0*y3 + x0,
x1*y0*y3,
x1*y1*y2 + x0*x1 + x0*x2 + x0*x3 + x1*x3 + x0*y0 + x0*y3 + x1 + y0 + y1 + 1,
x1*y1*y3 + x0*x1 + x1*x3 + x0*y0 + x1 + x2 + x3 + y0 + y1 + y3 + 1,
x1*y2*y3 + x0*x1 + x0*x2 + x1*x3 + x0*y0 + x0*y2 + x0*y3 + x0 + x1 + x2 + x3 + y0 + y1 + y3 + 1,
x2*x3*y0 + x0*x1 + x0*x3 + x1*x3 + x0*y2 + x0*y3 + x2 + x3 + y3,
x2*x3*y1 + x0*y1 + x0*y2 + x0*y3 + x3 + y0,
x2*x3*y2 + x1*x3 + x0*y1 + x0 + x2 + x3 + y3,
x2*x3*y3,
x2*y0*y1 + x0*x2 + x0*x3 + x0*y0 + x0*y1 + x0*y2 + x0,
x2*y0*y2 + x0*x2 + x1*x3 + x0*y1 + x0*y3 + x2 + x3 + y3,
x2*y0*y3 + x0*x2 + x0*y3 + x0,
x2*y1*y2 + x0*x1 + x0*x2 + x1*x3 + x0*y0 + x0*y3 + x0 + x1 + x2 + x3 + y0 + y1 + y3 + 1,
x2*y1*y3 + x0*x3 + x1*x3 + x0*y0 + x0*y1 + x0*y3 + y0 + y3,
x2*y2*y3 + x0*x1 + x0*x2 + x1*x3 + x0*y0 + x0*y3 + x0 + x1 + x2 + x3 + y0 + y1 + y3 + 1,
x3*y0*y1 + x0*x3 + x0*y1 + x0 + x2 + x3 + y3,
x3*y0*y2 + x0*y0 + y0,
x3*y0*y3 + x1*x3 + x0*y1 + x0*y2 + x0*y3 + y0,
x3*y1*y2 + x0*x2 + x0*x3 + x0*y3 + x2 + x3 + y3,
x3*y1*y3 + x0*x2 + x0*x3 + x0*y0 + x0*y2 + x0,
x3*y2*y3 + x0*x2 + x0*x3 + x1*x3 + x0*y0 + x0*y1 + x0*y3 + x0 + y0,
y0*y1*y2 + x0*x3 + x0 + x2 + x3 + y3,
y0*y1*y3 + x0*x3 + x0*y0 + x0*y2 + x0*y3,
y0*y2*y3 + x0*x3 + x1*x3 + x0*y0 + x0*y1 + y0,
y1*y2*y3 + x0*x1 + x0*x2 + x1*x3 + x0*y0 + x0*y3 + x0 + x1 + x2 + x3 + y0 + y1 + y3 + 1]
sage: S.interpolation_polynomial()
(a^2 + 1)*x^14 + x^13 + (a^3 + a^2)*x^11 + (a^2 + 1)*x^7 + a^2 + a
The SR_gf2_2 gives an example how use alternative polynomial representations of the S-Box for construction of polynomial systems.
TESTS:
sage: sr == loads(dumps(sr))
True
REFERENCES:
| [CMR05] | C. Cid, S. Murphy, M. Robshaw Small Scale Variants of the AES; in Proceedings of Fast Software Encryption 2005; LNCS 3557; Springer Verlag 2005; available at http://www.isg.rhul.ac.uk/~sean/smallAES-fse05.pdf |
| [CMR06] | C. Cid, S. Murphy, and M. Robshaw Algebraic Aspects of the Advanced Encryption Standard; Springer Verlag 2006 |
| [MR02] | (1, 2, 3, 4) S. Murphy, M. Robshaw Essential Algebraic Structure Within the AES; in Advances in Cryptology - CRYPTO 2002; LNCS 2442; Springer Verlag 2002 |
Return a small scale variant of the AES polynomial system constructor subject to the following conditions:
INPUT:
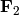 rather than
over
rather than
over 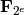 (default: False)
(default: False)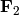 only)
only)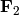 only)
only)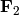 only)
only)EXAMPLES:
sage: sr = mq.SR(1, 1, 1, 4)
sage: ShiftRows = sr.shift_rows_matrix()
sage: MixColumns = sr.mix_columns_matrix()
sage: Lin = sr.lin_matrix()
sage: M = MixColumns * ShiftRows * Lin
sage: print sr.hex_str_matrix(M)
5 1 C 5
2 2 1 F
A 4 4 1
1 8 3 3
sage: sr = mq.SR(1, 2, 1, 4)
sage: ShiftRows = sr.shift_rows_matrix()
sage: MixColumns = sr.mix_columns_matrix()
sage: Lin = sr.lin_matrix()
sage: M = MixColumns * ShiftRows * Lin
sage: print sr.hex_str_matrix(M)
F 3 7 F A 2 B A
A A 5 6 8 8 4 9
7 8 8 2 D C C 3
4 6 C C 5 E F F
A 2 B A F 3 7 F
8 8 4 9 A A 5 6
D C C 3 7 8 8 2
5 E F F 4 6 C C
sage: sr = mq.SR(1, 2, 2, 4)
sage: ShiftRows = sr.shift_rows_matrix()
sage: MixColumns = sr.mix_columns_matrix()
sage: Lin = sr.lin_matrix()
sage: M = MixColumns * ShiftRows * Lin
sage: print sr.hex_str_matrix(M)
F 3 7 F 0 0 0 0 0 0 0 0 A 2 B A
A A 5 6 0 0 0 0 0 0 0 0 8 8 4 9
7 8 8 2 0 0 0 0 0 0 0 0 D C C 3
4 6 C C 0 0 0 0 0 0 0 0 5 E F F
A 2 B A 0 0 0 0 0 0 0 0 F 3 7 F
8 8 4 9 0 0 0 0 0 0 0 0 A A 5 6
D C C 3 0 0 0 0 0 0 0 0 7 8 8 2
5 E F F 0 0 0 0 0 0 0 0 4 6 C C
0 0 0 0 A 2 B A F 3 7 F 0 0 0 0
0 0 0 0 8 8 4 9 A A 5 6 0 0 0 0
0 0 0 0 D C C 3 7 8 8 2 0 0 0 0
0 0 0 0 5 E F F 4 6 C C 0 0 0 0
0 0 0 0 F 3 7 F A 2 B A 0 0 0 0
0 0 0 0 A A 5 6 8 8 4 9 0 0 0 0
0 0 0 0 7 8 8 2 D C C 3 0 0 0 0
0 0 0 0 4 6 C C 5 E F F 0 0 0 0
Bases: sage.crypto.mq.mpolynomialsystemgenerator.MPolynomialSystemGenerator
Perform the AddRoundKey operation on d using key.
INPUT:
EXAMPLE:
sage: sr = mq.SR(10, 4, 4, 4)
sage: D = sr.random_state_array()
sage: K = sr.random_state_array()
sage: sr.add_round_key(D, K) == K + D
True
Return the base field of self as determined by self.e.
EXAMPLE:
sage: sr = mq.SR(10, 2, 2, 4)
sage: sr.base_ring().polynomial()
a^4 + a + 1
The Rijndael polynomial:
sage: sr = mq.SR(10, 4, 4, 8)
sage: sr.base_ring().polynomial()
a^8 + a^4 + a^3 + a + 1
Return a block order for self where each round is a block.
EXAMPLE:
sage: sr = mq.SR(2, 1, 1, 4)
sage: sr.block_order()
degrevlex(16),degrevlex(16),degrevlex(4) term order
sage: P = sr.ring(order='block')
sage: print P.repr_long()
Polynomial Ring
Base Ring : Finite Field in a of size 2^4
Size : 36 Variables
Block 0 : Ordering : degrevlex
Names : k200, k201, k202, k203, x200, x201, x202, x203, w200, w201, w202, w203, s100, s101, s102, s103
Block 1 : Ordering : degrevlex
Names : k100, k101, k102, k103, x100, x101, x102, x103, w100, w101, w102, w103, s000, s001, s002, s003
Block 2 : Ordering : degrevlex
Names : k000, k001, k002, k003
Return a hex string for the provided AES state array/matrix.
INPUT:
EXAMPLE:
sage: sr = mq.SR(2, 2, 2, 4)
sage: k = sr.base_ring()
sage: A = matrix(k, 2, 2, [1, k.gen(), 0, k.gen()^2])
sage: sr.hex_str(A)
' 1 2 \n 0 4 \n'
sage: sr.hex_str(A, typ='vector')
'1024'
Return a two-dimensional AES-like representation of the matrix M.
That is, show the finite field elements as hex strings.
INPUT:
EXAMPLE:
sage: sr = mq.SR(2, 2, 2, 4)
sage: k = sr.base_ring()
sage: A = matrix(k, 2, 2, [1, k.gen(), 0, k.gen()^2])
sage: sr.hex_str_matrix(A)
' 1 2 \n 0 4 \n'
Return a one-dimensional AES-like representation of the matrix M.
That is, show the finite field elements as hex strings.
INPUT:
EXAMPLE:
sage: sr = mq.SR(2, 2, 2, 4)
sage: k = sr.base_ring()
sage: A = matrix(k, 2, 2, [1, k.gen(), 0, k.gen()^2])
sage: sr.hex_str_vector(A)
'1024'
Return True if d is a state array, i.e. has the correct dimensions and base field.
EXAMPLE:
sage: sr = mq.SR(2, 2, 4, 8)
sage: k = sr.base_ring()
sage: sr.is_state_array( matrix(k, 2, 4) )
True
sage: sr = mq.SR(2, 2, 4, 8)
sage: k = sr.base_ring()
sage: sr.is_state_array( matrix(k, 4, 4) )
False
Return 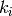 for a given
for a given  and
and 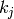 with
with 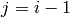 .
.
EXAMPLES:
sage: sr = mq.SR(10, 4, 4, 8, star=True, allow_zero_inversions=True)
sage: ki = sr.state_array()
sage: for i in range(10):
... ki = sr.key_schedule(ki, i+1)
sage: print sr.hex_str_matrix(ki)
B4 3E 23 6F
EF 92 E9 8F
5B E2 51 18
CB 11 CF 8E
Return polynomials for the  -th round of the key
schedule.
-th round of the key
schedule.
INPUT:
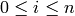 )
)EXAMPLE:
sage: sr = mq.SR(1, 1, 1, 4, gf2=True)
The 0-th subkey is the user provided key, so only conjugacy relations are added.
sage: sr.key_schedule_polynomials(0)
(k000^2 + k000, k001^2 + k001, k002^2 + k002, k003^2 + k003)
The 1-th subkey is derived from the user provided key according to the key schedule which is non-linear.
sage: sr.key_schedule_polynomials(1)
(k100 + s000 + s002 + s003,
k101 + s000 + s001 + s003 + 1,
k102 + s000 + s001 + s002 + 1,
k103 + s001 + s002 + s003 + 1,
k100^2 + k100, k101^2 + k101, k102^2 + k102, k103^2 + k103,
s000^2 + s000, s001^2 + s001, s002^2 + s002, s003^2 + s003,
s000*k000 + s003*k000 + s002*k001 + s001*k002 + s000*k003,
s000*k000 + s001*k000 + s000*k001 + s003*k001 + s002*k002 + s001*k003,
s001*k000 + s002*k000 + s000*k001 + s001*k001 + s000*k002 + s003*k002 + s002*k003,
s000*k000 + s002*k000 + s003*k000 + s000*k001 + s001*k001 + s002*k002 + s000*k003 + k000,
s001*k000 + s003*k000 + s001*k001 + s002*k001 + s000*k002 + s003*k002 + s001*k003 + k001,
s000*k000 + s002*k000 + s000*k001 + s002*k001 + s003*k001 + s000*k002 + s001*k002 + s002*k003 + k002,
s001*k000 + s002*k000 + s000*k001 + s003*k001 + s001*k002 + s003*k003 + k003,
s000*k000 + s001*k000 + s003*k000 + s001*k001 + s000*k002 + s002*k002 + s000*k003 + s000,
s002*k000 + s000*k001 + s001*k001 + s003*k001 + s001*k002 + s000*k003 + s002*k003 + s001,
s000*k000 + s001*k000 + s002*k000 + s002*k001 + s000*k002 + s001*k002 + s003*k002 + s001*k003 + s002,
s001*k000 + s000*k001 + s002*k001 + s000*k002 + s001*k003 + s003*k003 + s003,
s002*k000 + s001*k001 + s000*k002 + s003*k003 + 1)
Perform the MixColumns operation on d.
INPUT:
EXAMPLES:
sage: sr = mq.SR(10, 4, 4, 4)
sage: E = sr.state_array() + 1; E
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
sage: sr.mix_columns(E)
[ a a + 1 1 1]
[ 1 a a + 1 1]
[ 1 1 a a + 1]
[a + 1 1 1 a]
Return a new SR instance equal to this instance except for the parameters passed explicitly to this function.
INPUT:
EXAMPLE:
sage: sr = mq.SR(2,1,1,4); sr
SR(2,1,1,4)
sage: sr.ring().base_ring()
Finite Field in a of size 2^4
sage: sr2 = sr.new_generator(gf2=True); sr2
SR(2,1,1,4)
sage: sr2.ring().base_ring()
Finite Field of size 2
sage: sr3 = sr2.new_generator(correct_only=True)
sage: len(sr2.inversion_polynomials_single_sbox())
20
sage: len(sr3.inversion_polynomials_single_sbox())
19
Return a polynomial system for this small scale AES variant for a given plaintext-key pair.
If neither P, K nor C are provided, a random pair (P, K) will be generated. If P and C are provided no K needs to be provided.
INPUT:
EXAMPLE:
sage: sr = mq.SR(1, 1, 1, 4, gf2=True, polybori=True)
sage: P = sr.vector([0, 0, 1, 0])
sage: K = sr.vector([1, 0, 0, 1])
sage: F, s = sr.polynomial_system(P, K)
This returns a polynomial system:
sage: F
Polynomial System with 36 Polynomials in 20 Variables
and a solution:
sage: s # random -- maybe we need a better doctest here?
{k000: 1, k001: 0, k003: 1, k002: 0}
This solution is not the only solution that we can learn from the Groebner basis of the system.
sage: F.groebner_basis()[-3:]
[k000 + 1, k001, k003 + 1]
In particular we have two solutions:
sage: len(F.ideal().variety())
2
In the following example we provide C explicitly:
sage: C = sr(P,K)
sage: F,s = sr.polynomial_system(P=P, C=C)
sage: F
Polynomial System with 36 Polynomials in 20 Variables
Alternatively, we can use symbols for the P and C. First, we have to create a polynomial ring:
sage: sr = mq.SR(1, 1, 1, 4, gf2=True, polybori=True)
sage: R = sr.R
sage: vn = sr.varstrs("P",0,1,4) + R.variable_names() + sr.varstrs("C",0,1,4)
sage: R = BooleanPolynomialRing(len(vn),vn)
sage: sr.R = R
Now, we can construct the purely symbolic equation system:
sage: C = sr.vars("C",0); C
(C000, C001, C002, C003)
sage: P = sr.vars("P",0)
sage: F,s = sr.polynomial_system(P=P,C=C)
sage: [(k,v) for k,v in sorted(s.iteritems())] # this can be ignored
[(k003, 1), (k002, 1), (k001, 0), (k000, 0)]
sage: F
Polynomial System with 36 Polynomials in 28 Variables
sage: F.round(0)
(P000 + w100 + k000, P001 + w101 + k001, P002 + w102 + k002, P003 + w103 + k003)
sage: F.round(-2)
(k100 + x100 + x102 + x103 + C000, k101 + x100 + x101 + x103 + C001 + 1, ...)
Return a random element for self.
INPUT:
EXAMPLE:
sage: sr = mq.SR()
sage: sr.random_element()
[ a^3 + a + 1]
[ a^3 + 1]
[a^3 + a^2 + 1]
[a^3 + a^2 + a]
sage: sr.random_element('state_array')
[a + 1]
Return a random element in MatrixSpace(self.base_ring(), self.r, self.c).
EXAMPLE:
sage: sr = mq.SR(2, 2, 2, 4)
sage: sr.random_state_array()
[a^3 + a + 1 a + 1]
[ a + 1 a^2]
Return a random vector as it might appear in the algebraic expression of self.
EXAMPLE:
sage: sr = mq.SR(2, 2, 2, 4)
sage: sr.random_vector()
[ a^3 + a + 1]
[ a^3 + 1]
[a^3 + a^2 + 1]
[a^3 + a^2 + a]
[ a + 1]
[ a^2 + 1]
[ a]
[ a^2]
[ a + 1]
[ a^2 + 1]
[ a]
[ a^2]
[ a^2]
[ a + 1]
[ a^2 + 1]
[ a]
Note
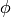 was already applied to the result.
was already applied to the result.
Construct a ring as a base ring for the polynomial system.
By default, variables are ordered in the reverse of their natural ordering, i.e. the reverse of as they appear.
INPUT:
The variable assignment is as follows:
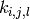 - subkey round
- subkey round  word
word  conjugate/bit
conjugate/bit 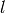
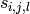 - subkey inverse round
- subkey inverse round  word
word  conjugate/bit
conjugate/bit 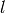
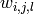 - inversion input round
- inversion input round  word
word  conjugate/bit
conjugate/bit 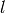
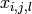 - inversion output round
- inversion output round  word
word  conjugate/bit
conjugate/bit 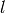
Note that the variables are ordered in column major ordering in the state array and that the bits are ordered in little endian ordering.
For example, if 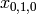 is a variable over
is a variable over 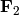 for
for
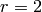 and
and 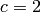 then refers to the most significant bit of
the entry in the position (1,0) in the state array matrix.
then refers to the most significant bit of
the entry in the position (1,0) in the state array matrix.
EXAMPLE:
sage: sr = mq.SR(2, 1, 1, 4)
sage: P = sr.ring(order='block')
sage: print P.repr_long()
Polynomial Ring
Base Ring : Finite Field in a of size 2^4
Size : 36 Variables
Block 0 : Ordering : degrevlex
Names : k200, k201, k202, k203, x200, x201, x202, x203, w200, w201, w202, w203, s100, s101, s102, s103
Block 1 : Ordering : degrevlex
Names : k100, k101, k102, k103, x100, x101, x102, x103, w100, w101, w102, w103, s000, s001, s002, s003
Block 2 : Ordering : degrevlex
Names : k000, k001, k002, k003
Return list of polynomials for a given round  .
.
If i == 0 a plaintext must be provided, if i == n a ciphertext must be provided.
INPUT:
OUTPUT: MPolynomialRoundSystem
EXAMPLE:
sage: sr = mq.SR(1, 1, 1, 4)
sage: k = sr.base_ring()
sage: p = [k.random_element() for _ in range(sr.r*sr.c)]
sage: sr.round_polynomials(0, plaintext=p)
(w100 + k000 + (a^2 + 1), w101 + k001 + (a), w102 + k002 + (a^2), w103 + k003 + (a + 1))
Return an S-Box object for this SR instance.
INPUT:
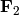 affine map when
computing the S-Box (default: False)
affine map when
computing the S-Box (default: False)EXAMPLE:
sage: sr = mq.SR(1,2,2,4, allow_zero_inversions=True)
sage: S = sr.sbox(); S
(6, 11, 5, 4, 2, 14, 7, 10, 9, 13, 15, 12, 3, 1, 0, 8)
sage: sr.sub_byte(0)
a^2 + a
sage: sage_eval(str(sr.sub_byte(0)), {'a':2})
6
sage: S(0)
6
sage: sr.sub_byte(1)
a^3 + a + 1
sage: sage_eval(str(sr.sub_byte(1)), {'a':2})
11
sage: S(1)
11
sage: sr = mq.SR(1,2,2,8, allow_zero_inversions=True)
sage: S = sr.sbox(); S
(99, 124, 119, 123, 242, 107, 111, 197, 48, 1, 103, 43,
254, 215, 171, 118, 202, 130, 201, 125, 250, 89, 71, 240,
173, 212, 162, 175, 156, 164, 114, 192, 183, 253, 147, 38,
54, 63, 247, 204, 52, 165, 229, 241, 113, 216, 49, 21, 4,
199, 35, 195, 24, 150, 5, 154, 7, 18, 128, 226, 235, 39,
178, 117, 9, 131, 44, 26, 27, 110, 90, 160, 82, 59, 214,
179, 41, 227, 47, 132, 83, 209, 0, 237, 32, 252, 177, 91,
106, 203, 190, 57, 74, 76, 88, 207, 208, 239, 170, 251,
67, 77, 51, 133, 69, 249, 2, 127, 80, 60, 159, 168, 81,
163, 64, 143, 146, 157, 56, 245, 188, 182, 218, 33, 16,
255, 243, 210, 205, 12, 19, 236, 95, 151, 68, 23, 196,
167, 126, 61, 100, 93, 25, 115, 96, 129, 79, 220, 34, 42,
144, 136, 70, 238, 184, 20, 222, 94, 11, 219, 224, 50, 58,
10, 73, 6, 36, 92, 194, 211, 172, 98, 145, 149, 228, 121,
231, 200, 55, 109, 141, 213, 78, 169, 108, 86, 244, 234,
101, 122, 174, 8, 186, 120, 37, 46, 28, 166, 180, 198,
232, 221, 116, 31, 75, 189, 139, 138, 112, 62, 181, 102,
72, 3, 246, 14, 97, 53, 87, 185, 134, 193, 29, 158, 225,
248, 152, 17, 105, 217, 142, 148, 155, 30, 135, 233, 206,
85, 40, 223, 140, 161, 137, 13, 191, 230, 66, 104, 65,
153, 45, 15, 176, 84, 187, 22)
sage: sr.sub_byte(0)
a^6 + a^5 + a + 1
sage: sage_eval(str(sr.sub_byte(0)), {'a':2})
99
sage: S(0)
99
sage: sr.sub_byte(1)
a^6 + a^5 + a^4 + a^3 + a^2
sage: sage_eval(str(sr.sub_byte(1)), {'a':2})
124
sage: S(1)
124
sage: sr = mq.SR(1,2,2,4, allow_zero_inversions=True)
sage: S = sr.sbox(inversion_only=True); S
(0, 1, 9, 14, 13, 11, 7, 6, 15, 2, 12, 5, 10, 4, 3, 8)
sage: S(0)
0
sage: S(1)
1
sage: S(sr.k.gen())
a^3 + 1
Return the S-Box constant which is added after 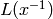 was
performed. That is 0x63 if e == 8 or 0x6 if e ==
4.
was
performed. That is 0x63 if e == 8 or 0x6 if e ==
4.
EXAMPLE:
sage: sr = mq.SR(10, 1, 1, 8)
sage: sr.sbox_constant()
a^6 + a^5 + a + 1
Perform the ShiftRows operation on d.
INPUT:
EXAMPLES:
sage: sr = mq.SR(10, 4, 4, 4)
sage: E = sr.state_array() + 1; E
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
sage: sr.shift_rows(E)
[1 0 0 0]
[1 0 0 0]
[1 0 0 0]
[1 0 0 0]
Convert the parameter to a state array.
INPUT:
EXAMPLES:
sage: sr = mq.SR(2, 2, 2, 4)
sage: k = sr.base_ring()
sage: e1 = [k.fetch_int(e) for e in range(2*2)]; e1
[0, 1, a, a + 1]
sage: e2 = sr.phi( Matrix(k, 2*2, 1, e1) )
sage: sr.state_array(e1) # note the column major ordering
[ 0 a]
[ 1 a + 1]
sage: sr.state_array(e2)
[ 0 a]
[ 1 a + 1]
sage: sr.state_array()
[0 0]
[0 0]
Perform SubByte on a single byte/halfbyte b.
A ZeroDivision exception is raised if an attempt is made to perform an inversion on the zero element. This can be disabled by passing allow_zero_inversion=True to the constructor. A zero inversion can result in an inconsistent equation system.
INPUT:
EXAMPLE:
The S-Box table for  :
:
sage: sr = mq.SR(1, 1, 1, 4, allow_zero_inversions=True)
sage: for e in sr.base_ring():
... print '% 20s % 20s'%(e, sr.sub_byte(e))
0 a^2 + a
a a^2 + 1
a^2 a
a^3 a^3 + 1
a + 1 a^2
a^2 + a a^2 + a + 1
a^3 + a^2 a + 1
a^3 + a + 1 a^3 + a^2
a^2 + 1 a^3 + a^2 + a
a^3 + a a^3 + a^2 + a + 1
a^2 + a + 1 a^3 + a
a^3 + a^2 + a 0
a^3 + a^2 + a + 1 a^3
a^3 + a^2 + 1 1
a^3 + 1 a^3 + a^2 + 1
1 a^3 + a + 1
Perform the non-linear transform on d.
INPUT:
EXAMPLE:
sage: sr = mq.SR(2, 1, 2, 8, gf2=True)
sage: k = sr.base_ring()
sage: A = Matrix(k, 1, 2 , [k(1), k.gen()])
sage: sr.sub_bytes(A)
[ a^6 + a^5 + a^4 + a^3 + a^2 a^6 + a^5 + a^4 + a^2 + a + 1]
Return a format string which is understood by print et al.
If a numerical value is omitted, the default value of self is used. The numerical values (n, rc, e) are used to determine the width of the respective fields in the format string.
INPUT:
EXAMPLE:
sage: sr = mq.SR(1, 2, 2, 4)
sage: sr.varformatstr('x')
'x%01d%01d%01d'
sage: sr.varformatstr('x', n=1000)
'x%03d%03d%03d'
Return a dictionary to access variables in self.R by their names.
EXAMPLE:
sage: sr = mq.SR(1,1,1,4)
sage: sr.variable_dict()
{'x101': x101, 'x100': x100, 'x103': x103, 'x102': x102,
's002': s002, 'w100': w100, 'w101': w101, 'w102': w102,
'w103': w103, 'k100': k100, 'k101': k101, 'k102': k102,
'k103': k103, 's003': s003, 's001': s001, 'k002': k002,
'k001': k001, 'k000': k000, 'k003': k003, 's000': s000}
sage: sr = mq.SR(1,1,1,4,gf2=True)
sage: sr.variable_dict()
{'x101': x101, 'x100': x100, 'x103': x103, 'x102': x102,
's002': s002, 'w100': w100, 'w101': w101, 'w102': w102,
'w103': w103, 'k100': k100, 'k101': k101, 'k102': k102,
'k103': k103, 's003': s003, 's001': s001, 'k002': k002,
'k001': k001, 'k000': k000, 'k003': k003, 's000': s000}
Return a list of variables in self.
INPUT:
EXAMPLE:
sage: sr = mq.SR(10, 1, 2, 4)
sage: sr.vars('x', 2)
(x200, x201, x202, x203, x210, x211, x212, x213)
Return a string representing a variable for the small scale AES subject to the given constraints.
INPUT:
EXAMPLE:
sage: sr = mq.SR(10, 1, 2, 4)
sage: sr.varstr('x', 2, 1, 1)
'x211'
Return a list of strings representing variables in self.
INPUT:
EXAMPLE:
sage: sr = mq.SR(10, 1, 2, 4)
sage: sr.varstrs('x', 2)
('x200', 'x201', 'x202', 'x203', 'x210', 'x211', 'x212', 'x213')
Bases: sage.crypto.mq.sr.SR_generic
The operation 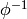 from [MR02] or the inverse of self.phi.
from [MR02] or the inverse of self.phi.
INPUT:
EXAMPLE:
sage: sr = mq.SR(gf2=True)
sage: A = sr.random_state_array()
sage: A
[a^3 + a + 1]
sage: sr.antiphi(sr.phi(A)) == A
True
Return list of field polynomials for a given round i and name name.
INPUT:
EXAMPLE:
sage: sr = mq.SR(3, 1, 1, 8, gf2=True)
sage: sr.field_polynomials('x', 2)
[x200^2 + x200, x201^2 + x201,
x202^2 + x202, x203^2 + x203,
x204^2 + x204, x205^2 + x205,
x206^2 + x206, x207^2 + x207]
sage: sr = mq.SR(3, 1, 1, 8, gf2=True, polybori=True)
sage: sr.field_polynomials('x', 2)
[]
Return polynomials to represent the inversion in the AES S-Box.
INPUT:
EXAMPLE:
sage: sr = mq.SR(1, 1, 1, 8, gf2=True)
sage: xi = sr.vars('x', 1)
sage: wi = sr.vars('w', 1)
sage: sr.inversion_polynomials(xi, wi, len(xi))[:3]
[x100*w100 + x102*w100 + x103*w100 + x107*w100 + x101*w101
+ x102*w101 + x106*w101 + x100*w102 + x101*w102 +
x105*w102 + x100*w103 + x104*w103 + x103*w104 + x102*w105
+ x101*w106 + x100*w107, x101*w100 + x103*w100 + x104*w100
+ x100*w101 + x102*w101 + x103*w101 + x107*w101 +
x101*w102 + x102*w102 + x106*w102 + x100*w103 + x101*w103
+ x105*w103 + x100*w104 + x104*w104 + x103*w105 +
x102*w106 + x101*w107, x102*w100 + x104*w100 + x105*w100 +
x101*w101 + x103*w101 + x104*w101 + x100*w102 + x102*w102
+ x103*w102 + x107*w102 + x101*w103 + x102*w103 +
x106*w103 + x100*w104 + x101*w104 + x105*w104 + x100*w105
+ x104*w105 + x103*w106 + x102*w107]
Return inversion polynomials of a single S-Box.
INPUT:
EXAMPLES:
sage: sr = mq.SR(1, 1, 1, 8, gf2=True)
sage: len(sr.inversion_polynomials_single_sbox())
24
sage: len(sr.inversion_polynomials_single_sbox(correct_only=True))
23
sage: len(sr.inversion_polynomials_single_sbox(biaffine_only=False))
40
sage: len(sr.inversion_polynomials_single_sbox(biaffine_only=False, correct_only=True))
39
sage: sr = mq.SR(1, 1, 1, 8, gf2=True)
sage: l0 = sr.inversion_polynomials_single_sbox(); len(l0)
24
sage: l1 = sr.inversion_polynomials_single_sbox(correct_only=True); len(l1)
23
sage: l2 = sr.inversion_polynomials_single_sbox(biaffine_only=False); len(l2)
40
sage: l3 = sr.inversion_polynomials_single_sbox(biaffine_only=False, correct_only=True); len(l3)
39
sage: set(l0) == set(sr._inversion_polynomials_single_sbox())
True
sage: set(l1) == set(sr._inversion_polynomials_single_sbox(correct_only=True))
True
sage: set(l2) == set(sr._inversion_polynomials_single_sbox(biaffine_only=False))
True
sage: set(l3) == set(sr._inversion_polynomials_single_sbox(biaffine_only=False, correct_only=True))
True
sage: sr = mq.SR(1, 1, 1, 4, gf2=True)
sage: l0 = sr.inversion_polynomials_single_sbox(); len(l0)
12
sage: l1 = sr.inversion_polynomials_single_sbox(correct_only=True); len(l1)
11
sage: l2 = sr.inversion_polynomials_single_sbox(biaffine_only=False); len(l2)
20
sage: l3 = sr.inversion_polynomials_single_sbox(biaffine_only=False, correct_only=True); len(l3)
19
sage: set(l0) == set(sr._inversion_polynomials_single_sbox())
True
sage: set(l1) == set(sr._inversion_polynomials_single_sbox(correct_only=True))
True
sage: set(l2) == set(sr._inversion_polynomials_single_sbox(biaffine_only=False))
True
sage: set(l3) == set(sr._inversion_polynomials_single_sbox(biaffine_only=False, correct_only=True))
True
Return True if the given matrix satisfies the conditions for a vector as it appears in the algebraic expression of self.
INPUT:
EXAMPLE:
sage: sr = mq.SR(gf2=True)
sage: sr
SR(1,1,1,4)
sage: k = sr.base_ring()
sage: A = Matrix(k, 1, 1, [k.gen()])
sage: B = sr.vector(A)
sage: sr.is_vector(A)
False
sage: sr.is_vector(B)
True
Return the Lin matrix.
If no length is provided, the standard state space size is used. The key schedule calls this method with an explicit length argument because only self.r S-Box applications are performed in the key schedule.
INPUT:
EXAMPLE:
sage: sr = mq.SR(1, 1, 1, 4, gf2=True)
sage: sr.lin_matrix()
[1 0 1 1]
[1 1 0 1]
[1 1 1 0]
[0 1 1 1]
Return the MixColumns matrix.
EXAMPLE:
sage: sr = mq.SR(1, 2, 2, 4, gf2=True)
sage: s = sr.random_state_array()
sage: r1 = sr.mix_columns(s)
sage: r2 = sr.state_array(sr.mix_columns_matrix() * sr.vector(s))
sage: r1 == r2
True
The operation 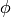 from [MR02]
from [MR02]
Given a list/matrix of elements in 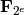 , return a
matching list/matrix of elements in
, return a
matching list/matrix of elements in 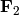 .
.
INPUT:
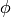 on.
on.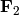 as l over
as l over 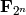 (default: False).
(default: False).EXAMPLE:
sage: sr = mq.SR(2, 1, 2, 4, gf2=True)
sage: k = sr.base_ring()
sage: A = matrix(k, 1, 2, [k.gen(), 0] )
sage: sr.phi(A)
[0 0]
[0 0]
[1 0]
[0 0]
Return the ShiftRows matrix.
EXAMPLE:
sage: sr = mq.SR(1, 2, 2, 4, gf2=True)
sage: s = sr.random_state_array()
sage: r1 = sr.shift_rows(s)
sage: r2 = sr.state_array( sr.shift_rows_matrix() * sr.vector(s) )
sage: r1 == r2
True
Constructs a vector suitable for the algebraic representation of SR.
INPUT:
EXAMPLE:
sage: sr = mq.SR(gf2=True)
sage: sr
SR(1,1,1,4)
sage: k = sr.base_ring()
sage: A = Matrix(k, 1, 1, [k.gen()])
sage: sr.vector(A)
[0]
[0]
[1]
[0]
Bases: sage.crypto.mq.sr.SR_gf2
This is an example how to customize the SR constructor.
In this example, we replace the S-Box inversion polynomials by the polynomials generated by the S-Box class.
Return inversion polynomials of a single S-Box.
INPUT:
EXAMPLES:
sage: from sage.crypto.mq.sr import SR_gf2_2
sage: e = 4
sage: sr = SR_gf2_2(1, 1, 1, e)
sage: P = PolynomialRing(GF(2),['x%d'%i for i in range(e)] + ['w%d'%i for i in range(e)],order='lex')
sage: X,W = P.gens()[:e],P.gens()[e:]
sage: sr.inversion_polynomials_single_sbox(X, W, groebner=True)
[x0 + w0*w1*w2 + w0*w1 + w0*w2 + w0*w3 + w0 + w1 + w2,
x1 + w0*w1*w3 + w0*w3 + w0 + w1*w3 + w1 + w2*w3,
x2 + w0*w2*w3 + w0*w2 + w0 + w1*w2 + w1*w3 + w2*w3,
x3 + w0*w1*w2 + w0 + w1*w2*w3 + w1*w2 + w1*w3 + w1 + w2 + w3]
sage: from sage.crypto.mq.sr import SR_gf2_2
sage: e = 4
sage: sr = SR_gf2_2(1, 1, 1, e)
sage: sr.inversion_polynomials_single_sbox()
[w3*w1 + w3*w0 + w3*x2 + w3*x1 + w3 + w2*w1 + w1 + x3 + x2 + x1,
w3*w2 + w3*w1 + w3*x3 + w2 + w1 + x3,
w3*w2 + w3*w1 + w3*x2 + w3 + w2*x3 + x2 + x1,
w3*w2 + w3*w1 + w3*x3 + w3*x2 + w3*x1 + w3 + w2*x2 + w0 + x3 + x2 + x1 + x0,
w3*w2 + w3*w1 + w3*x1 + w3*x0 + w2*x1 + w0 + x3 + x0,
w3*w2 + w3*w1 + w3*w0 + w3*x2 + w3*x1 + w2*w0 + w2*x0 + w0 + x3 + x2 + x1 + x0,
w3*w2 + w3*x1 + w3 + w2*w0 + w1*w0 + w1 + x3 + x2,
w3*w2 + w3*w1 + w3*x1 + w1*x3 + x3 + x2 + x1,
w3*x3 + w3*x2 + w3*x0 + w3 + w1*x2 + w1 + w0 + x2 + x0,
w3*w2 + w3*w1 + w3*x2 + w3*x1 + w1*x1 + w1 + w0 + x2 + x0,
w3*w2 + w3*w1 + w3*w0 + w3*x3 + w3*x1 + w2*w0 + w1*x0 + x3 + x2,
w3*w2 + w3*w1 + w3*x2 + w3*x1 + w3*x0 + w3 + w1 + w0*x3 + x3 + x2,
w3*w2 + w3*w1 + w3*w0 + w3*x3 + w3 + w2*w0 + w1 + w0*x2 + x3 + x2,
w3*w0 + w3*x2 + w2*w0 + w0*x1 + w0 + x3 + x1 + x0,
w3*w0 + w3*x3 + w3*x0 + w2*w0 + w1 + w0*x0 + w0 + x3 + x2,
w3*w2 + w3 + w1 + x3*x2 + x3 + x1,
w3*w2 + w3*x3 + w1 + x3*x1 + x3 + x2,
w3*w2 + w3*w0 + w3*x3 + w3*x2 + w3*x1 + w0 + x3*x0 + x1 + x0,
w3*w2 + w3*w1 + w3*w0 + w3*x3 + w1 + w0 + x2*x1 + x2 + x0,
w3*w2 + w2*w0 + w1 + x3 + x2*x0,
w3*x3 + w3*x1 + w2*w0 + w1 + x3 + x2 + x1*x0 + x1]
TESTS:
Note that biaffine_only and correct_only are always ignored. The former is always false while the second is always true. They are only accepted for compatibility with the base class.
sage: from sage.crypto.mq.sr import SR_gf2_2 sage: e = 4 sage: sr = SR_gf2_2(1, 1, 1, e) sage: l = sr.inversion_polynomials_single_sbox() sage: l == sr.inversion_polynomials_single_sbox(biaffine_only=True, correct_only=False) True
Bases: sage.crypto.mq.sr.SR_generic
Small Scale Variants of the AES polynomial system constructor over
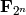 .
.
The operation 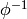 from [MR02] or the inverse of self.phi.
from [MR02] or the inverse of self.phi.
INPUT:
EXAMPLE:
sage: sr = mq.SR()
sage: A = sr.random_state_array()
sage: A
[a^3 + a + 1]
sage: sr.antiphi(sr.phi(A)) == A
True
Return list of conjugacy polynomials for a given round i and name name.
INPUT:
EXAMPLE:
sage: sr = mq.SR(3, 1, 1, 8)
sage: sr.field_polynomials('x', 2)
[x200^2 + x201,
x201^2 + x202,
x202^2 + x203,
x203^2 + x204,
x204^2 + x205,
x205^2 + x206,
x206^2 + x207,
x207^2 + x200]
Return polynomials to represent the inversion in the AES S-Box.
INPUT:
EXAMPLE:
sage: sr = mq.SR(1, 1, 1, 8)
sage: R = sr.ring()
sage: xi = Matrix(R, 8, 1, sr.vars('x', 1))
sage: wi = Matrix(R, 8, 1, sr.vars('w', 1))
sage: sr.inversion_polynomials(xi, wi, 8)
[x100*w100 + 1,
x101*w101 + 1,
x102*w102 + 1,
x103*w103 + 1,
x104*w104 + 1,
x105*w105 + 1,
x106*w106 + 1,
x107*w107 + 1]
Return True if d can be used as a vector for self.
EXAMPLE:
sage: sr = mq.SR()
sage: sr
SR(1,1,1,4)
sage: k = sr.base_ring()
sage: A = Matrix(k, 1, 1, [k.gen()])
sage: B = sr.vector(A)
sage: sr.is_vector(A)
False
sage: sr.is_vector(B)
True
Return the Lin matrix.
If no length is provided, the standard state space size is used. The key schedule calls this method with an explicit length argument because only self.r S-Box applications are performed in the key schedule.
INPUT:
EXAMPLE:
sage: sr = mq.SR(1, 1, 1, 4)
sage: sr.lin_matrix()
[ a^2 + 1 1 a^3 + a^2 a^2 + 1]
[ a a 1 a^3 + a^2 + a + 1]
[ a^3 + a a^2 a^2 1]
[ 1 a^3 a + 1 a + 1]
Return the MixColumns matrix.
EXAMPLE:
sage: sr = mq.SR(1, 2, 2, 4)
sage: s = sr.random_state_array()
sage: r1 = sr.mix_columns(s)
sage: r2 = sr.state_array(sr.mix_columns_matrix() * sr.vector(s))
sage: r1 == r2
True
The operation 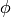 from [MR02]
from [MR02]
Projects state arrays to their algebraic representation.
INPUT:
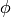 on.
on.EXAMPLE:
sage: sr = mq.SR(2, 1, 2, 4)
sage: k = sr.base_ring()
sage: A = matrix(k, 1, 2, [k.gen(), 0] )
sage: sr.phi(A)
[ a 0]
[ a^2 0]
[ a + 1 0]
[a^2 + 1 0]
Return the ShiftRows matrix.
EXAMPLE:
sage: sr = mq.SR(1, 2, 2, 4)
sage: s = sr.random_state_array()
sage: r1 = sr.shift_rows(s)
sage: r2 = sr.state_array( sr.shift_rows_matrix() * sr.vector(s) )
sage: r1 == r2
True
Constructs a vector suitable for the algebraic representation of SR, i.e. BES.
INPUT:
EXAMPLE:
sage: sr = mq.SR()
sage: sr
SR(1,1,1,4)
sage: k = sr.base_ring()
sage: A = Matrix(k, 1, 1, [k.gen()])
sage: sr.vector(A)
[ a]
[ a^2]
[ a + 1]
[a^2 + 1]
Test all combinations of r, c, e and n in (1,
2) for consistency of random encryptions and their polynomial
systems. 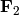 and
and 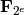 systems are tested. This test takes
a while.
systems are tested. This test takes
a while.
INPUT:
TESTS:
sage: from sage.crypto.mq.sr import test_consistency
sage: test_consistency(1) # long time -- calling w/ max_n = 2 requires a LOT of RAM (>> 2GB, evidently). Calling w/ max_n = 1 is far more manageable.
True
The above doctest used to fail on a machine with “only” 2GB RAM. Using max_n = 1 appears to be a more reasonable memory usage.