Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »

A skew partition 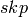 of size
of size  is a pair of
partitions
is a pair of
partitions ![[p_1, p_2]](../../_images/math/f01667d0f571e3ef2e2db26a28916da4ea9653af.png) where
where 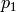 is a
partition of the integer
is a
partition of the integer 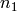 ,
, 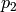 is a
partition of the integer
is a
partition of the integer 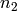 ,
, 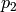 is an inner
partition of
is an inner
partition of 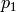 , and
, and 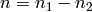 . We say
that
. We say
that 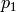 and
and 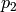 are respectively the inner
and outer partitions of
are respectively the inner
and outer partitions of 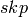 .
.
A skew partition can be depicted by a diagram made of rows of
cells, in the same way as a partition. Only the cells of the outer
partition 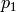 which are not in the inner partition
which are not in the inner partition
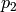 appear in the picture. For example, this is the
diagram of the skew partition [[5,4,3,1],[3,3,1]].
appear in the picture. For example, this is the
diagram of the skew partition [[5,4,3,1],[3,3,1]].
sage: print SkewPartition([[5,4,3,1],[3,3,1]]).diagram()
##
#
##
#
A skew partition can be connected, which can easily be described in graphic terms: for each pair of consecutive rows, there are at least two cells (one in each row) which have a common edge. This is the diagram of the connected skew partition [[5,4,3,1],[3,1]]:
sage: print SkewPartition([[5,4,3,1],[3,1]]).diagram()
##
###
###
#
sage: SkewPartition([[5,4,3,1],[3,1]]).is_connected()
True
The first example of a skew partition is not a connected one.
Applying a reflection with respect to the main diagonal yields the diagram of the conjugate skew partition, here [[4,3,3,2,1],[3,3,2]]:
sage: SkewPartition([[5,4,3,1],[3,3,1]]).conjugate()
[[4, 3, 3, 2, 1], [3, 2, 2]]
sage: print SkewPartition([[5,4,3,1],[3,3,1]]).conjugate().diagram()
#
#
#
##
#
The outer corners of a skew partition are the corners of its outer partition. The inner corners are the internal corners of the outer partition when the inner partition is taken off. Shown below are the coordinates of the inner and outer corners.
sage: SkewPartition([[5,4,3,1],[3,3,1]]).outer_corners()
[(0, 4), (1, 3), (2, 2), (3, 0)]
sage: SkewPartition([[5,4,3,1],[3,3,1]]).inner_corners()
[(0, 3), (2, 1), (3, 0)]
EXAMPLES:
There are 9 skew partitions of size 3, with no empty row nor empty column:
sage: SkewPartitions(3).cardinality()
9
sage: SkewPartitions(3).list()
[[[3], []],
[[2, 1], []],
[[3, 1], [1]],
[[2, 2], [1]],
[[3, 2], [2]],
[[1, 1, 1], []],
[[2, 2, 1], [1, 1]],
[[2, 1, 1], [1]],
[[3, 2, 1], [2, 1]]]
There are 4 connected skew partitions of size 3:
sage: SkewPartitions(3, overlap=1).cardinality()
4
sage: SkewPartitions(3, overlap=1).list()
[[[3], []], [[2, 1], []], [[2, 2], [1]], [[1, 1, 1], []]]
This is the conjugate of the skew partition [[4,3,1],[2]]
sage: SkewPartition([[4,3,1],[2]]).conjugate()
[[3, 2, 2, 1], [1, 1]]
Geometrically, we just applied a reflection with respect to the main diagonal on the diagram of the partition. Of course, this operation is an involution:
sage: SkewPartition([[4,3,1],[2]]).conjugate().conjugate()
[[4, 3, 1], [2]]
The jacobi_trudy() method computes the Jacobi-Trudi matrix. See Macdonald I.-G., (1995), “Symmetric Functions and Hall Polynomials”, Oxford Science Publication for a definition and discussion.
sage: SkewPartition([[4,3,1],[2]]).jacobi_trudi()
[h[2] h[] 0]
[h[5] h[3] h[]]
[h[6] h[4] h[1]]
This example shows how to compute the corners of a skew partition.
sage: SkewPartition([[4,3,1],[2]]).inner_corners()
[(0, 2), (1, 0)]
sage: SkewPartition([[4,3,1],[2]]).outer_corners()
[(0, 3), (1, 2), (2, 0)]
Returns the skew partition object corresponding to skp.
EXAMPLES:
sage: skp = SkewPartition([[3,2,1],[2,1]]); skp
[[3, 2, 1], [2, 1]]
sage: skp.inner()
[2, 1]
sage: skp.outer()
[3, 2, 1]
Bases: sage.combinat.combinat.CombinatorialObject
Returns the coordinates of the cells of self. Coordinates are given as (row-index, column-index) and are 0 based.
EXAMPLES:
sage: SkewPartition([[4, 3, 1], [2]]).cells()
[(0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (2, 0)]
sage: SkewPartition([[4, 3, 1], []]).cells()
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (2, 0)]
sage: SkewPartition([[2], []]).cells()
[(0, 0), (0, 1)]
Returns the column lengths of the skew partition.
EXAMPLES:
sage: SkewPartition([[3,2,1],[1,1]]).column_lengths()
[1, 2, 1]
sage: SkewPartition([[5,2,2,2],[2,1]]).column_lengths()
[2, 3, 1, 1, 1]
Returns the set of cells in the lines of lambda which intersect the skew partition.
EXAMPLES:
sage: skp = SkewPartition([[3,2,1],[2,1]])
sage: cells = Set([ (0,0), (0, 1), (0,2), (1, 0), (1, 1), (2, 0)])
sage: skp.columns_intersection_set() == cells
True
Returns the conjugate of the skew partition skp.
EXAMPLES:
sage: SkewPartition([[3,2,1],[2]]).conjugate()
[[3, 2, 1], [1, 1]]
Returns the Ferrers diagram of self.
EXAMPLES:
sage: print SkewPartition([[5,4,3,1],[3,3,1]]).ferrers_diagram()
##
#
##
#
sage: print SkewPartition([[5,4,3,1],[3,1]]).diagram()
##
###
###
#
Returns the Ferrers diagram of self.
EXAMPLES:
sage: print SkewPartition([[5,4,3,1],[3,3,1]]).ferrers_diagram()
##
#
##
#
sage: print SkewPartition([[5,4,3,1],[3,1]]).diagram()
##
###
###
#
Returns the inner partition of the skew partition.
EXAMPLES:
sage: SkewPartition([[3,2,1],[1,1]]).inner()
[1, 1]
Returns a list of the inner corners of the skew partition skp.
EXAMPLES:
sage: SkewPartition([[4, 3, 1], [2]]).inner_corners()
[(0, 2), (1, 0)]
sage: SkewPartition([[4, 3, 1], []]).inner_corners()
[(0, 0)]
Returns True if self is a connected skew partition.
A skew partition is said to be connected if for each pair of consecutive rows, there are at least two cells (one in each row) which have a common edge.
EXAMPLES:
sage: SkewPartition([[5,4,3,1],[3,3,1]]).is_connected()
False
sage: SkewPartition([[5,4,3,1],[3,1]]).is_connected()
True
Returns True if n = self.overlap()
See also
EXAMPLES:
sage: SkewPartition([[5,4,3,1],[3,1]]).is_overlap(1)
True
EXAMPLES:
sage: SkewPartition([[3,2,1],[2,1]]).jacobi_trudi()
[h[1] 0 0]
[h[3] h[1] 0]
[h[5] h[3] h[1]]
sage: SkewPartition([[4,3,2],[2,1]]).jacobi_trudi()
[h[2] h[] 0]
[h[4] h[2] h[]]
[h[6] h[4] h[2]]
Returns the k-conjugate of the skew partition.
EXAMPLES:
sage: SkewPartition([[3,2,1],[2,1]]).k_conjugate(3)
[[2, 1, 1, 1, 1], [2, 1]]
sage: SkewPartition([[3,2,1],[2,1]]).k_conjugate(4)
[[2, 2, 1, 1], [2, 1]]
sage: SkewPartition([[3,2,1],[2,1]]).k_conjugate(5)
[[3, 2, 1], [2, 1]]
Returns the outer partition of the skew partition.
EXAMPLES:
sage: SkewPartition([[3,2,1],[1,1]]).outer()
[3, 2, 1]
Returns a list of the outer corners of the skew partition skp.
EXAMPLES:
sage: SkewPartition([[4, 3, 1], [2]]).outer_corners()
[(0, 3), (1, 2), (2, 0)]
Returns the overlap of self.
The overlap of two consecutive rows in a skew partition is the number of pairs of cells (one in each row) that share a common edge. This number can be positive, zero, or negative.
The overlap of a skew partition is the minimum of the overlap of the consecutive rows, or infinity in the case of at most one row. If the overlap is positive, then the skew partition is called connected.
EXAMPLES:
sage: SkewPartition([[],[]]).overlap()
+Infinity
sage: SkewPartition([[1],[]]).overlap()
+Infinity
sage: SkewPartition([[10],[]]).overlap()
+Infinity
sage: SkewPartition([[10],[2]]).overlap()
+Infinity
sage: SkewPartition([[10,1],[2]]).overlap()
-1
sage: SkewPartition([[10,10],[1]]).overlap()
9
Computation of the coefficients which appear in the Pieri formula for Macdonald polynomials given in his book ( Chapter 6.6 formula 6.24(ii) )
EXAMPLES:
sage: SkewPartition([[3,2,1],[2,1]]).pieri_macdonald_coeffs()
1
sage: SkewPartition([[3,2,1],[2,2]]).pieri_macdonald_coeffs()
(q^2*t^3 - q^2*t - t^2 + 1)/(q^2*t^3 - q*t^2 - q*t + 1)
sage: SkewPartition([[3,2,1],[2,2,1]]).pieri_macdonald_coeffs()
(q^6*t^8 - q^6*t^6 - q^4*t^7 - q^5*t^5 + q^4*t^5 - q^3*t^6 + q^5*t^3 + 2*q^3*t^4 + q*t^5 - q^3*t^2 + q^2*t^3 - q*t^3 - q^2*t - t^2 + 1)/(q^6*t^8 - q^5*t^7 - q^5*t^6 - q^4*t^6 + q^3*t^5 + 2*q^3*t^4 + q^3*t^3 - q^2*t^2 - q*t^2 - q*t + 1)
sage: SkewPartition([[3,3,2,2],[3,2,2,1]]).pieri_macdonald_coeffs()
(q^5*t^6 - q^5*t^5 + q^4*t^6 - q^4*t^5 - q^4*t^3 + q^4*t^2 - q^3*t^3 - q^2*t^4 + q^3*t^2 + q^2*t^3 - q*t^4 + q*t^3 + q*t - q + t - 1)/(q^5*t^6 - q^4*t^5 - q^3*t^4 - q^3*t^3 + q^2*t^3 + q^2*t^2 + q*t - 1)
The quotient map extended to skew partitions.
EXAMPLES:
sage: SkewPartition([[3, 3, 2, 1], [2, 1]]).quotient(2)
[[[3], []], [[], []]]
Returns the row lengths of the skew partition.
EXAMPLES:
sage: SkewPartition([[3,2,1],[1,1]]).row_lengths()
[2, 1, 1]
Returns the set of cells in the lines of lambda which intersect the skew partition.
EXAMPLES:
sage: skp = SkewPartition([[3,2,1],[2,1]])
sage: cells = Set([ (0,0), (0, 1), (0,2), (1, 0), (1, 1), (2, 0)])
sage: skp.rows_intersection_set() == cells
True
Returns the size of the skew partition.
EXAMPLES:
sage: SkewPartition([[3,2,1],[1,1]]).size()
4
Returns a directed acyclic graph corresponding to the skew partition.
EXAMPLES:
sage: dag = SkewPartition([[3, 2, 1], [1, 1]]).to_dag()
sage: dag.edges()
[('0,1', '0,2', None), ('0,1', '1,1', None)]
sage: dag.vertices()
['0,1', '0,2', '1,1', '2,0']
Returns self as a list of lists.
EXAMPLES:
sage: s = SkewPartition([[4,3,1],[2]])
sage: s.to_list()
[[4, 3, 1], [2]]
sage: type(s.to_list())
<type 'list'>
Returns the combinatorial class of skew partitions.
EXAMPLES:
sage: SkewPartitions(4)
Skew partitions of 4
sage: SkewPartitions(4).cardinality()
28
sage: SkewPartitions(row_lengths=[2,1,2])
Skew partitions with row lengths [2, 1, 2]
sage: SkewPartitions(4, overlap=2)
Skew partitions of 4 with overlap of 2
sage: SkewPartitions(4, overlap=2).list()
[[[4], []], [[2, 2], []]]
Bases: sage.combinat.combinat.CombinatorialClass
TESTS:
sage: SkewPartitions().list()
...
NotImplementedError
Bases: sage.combinat.combinat.CombinatorialClass
The combinatorial class of skew partitions with given size (and horizontal minimal overlap).
Returns the number of skew partitions of the integer n.
EXAMPLES:
sage: SkewPartitions(0).cardinality()
1
sage: SkewPartitions(4).cardinality()
28
sage: SkewPartitions(5).cardinality()
87
sage: SkewPartitions(4, overlap=1).cardinality()
9
sage: SkewPartitions(5, overlap=1).cardinality()
20
sage: s = SkewPartitions(5, overlap=-1)
sage: s.cardinality() == len(s.list())
True
Bases: sage.combinat.combinat.CombinatorialClass
The combinatorial class of all skew partitions with given row lengths.
Returns a list of all the skew partitions that have row lengths given by the composition self.co.
EXAMPLES:
sage: SkewPartitions(row_lengths=[2,2]).list()
[[[2, 2], []], [[3, 2], [1]], [[4, 2], [2]]]
sage: SkewPartitions(row_lengths=[2,2], overlap=1).list()
[[[2, 2], []], [[3, 2], [1]]]
Construct a partition from its row lengths and column lengths.
INPUT:
- rowL – a composition or a list of positive integers
- colL – a composition or a list of positive integers
OUTPUT:
- If it exists the unique skew-partitions with row lengths rowL and column lengths colL.
- Raise a ValueError if rowL and colL are not compatible.
EXAMPLES:
sage: from sage.combinat.skew_partition import from_row_and_column_length
sage: print from_row_and_column_length([3,1,2,2],[2,3,1,1,1]).diagram()
###
#
##
##
sage: from_row_and_column_length([],[])
[[], []]
sage: from_row_and_column_length([1],[1])
[[1], []]
sage: from_row_and_column_length([2,1],[2,1])
[[2, 1], []]
sage: from_row_and_column_length([1,2],[1,2])
[[2, 2], [1]]
sage: from_row_and_column_length([1,2],[1,3])
...
ValueError: Sum mismatch : [1, 2] and [1, 3]
sage: from_row_and_column_length([3,2,1,2],[2,3,1,1,1])
...
ValueError: Incompatible row and column length : [3, 2, 1, 2] and [2, 3, 1, 1, 1]
Warning
If some rows and columns have length zero, there is no way to retrieve unambiguously the skew partition. We therefore raise a ValueError. For examples here are two skew partitions with the same row and column lengths:
sage: skp1 = SkewPartition([[2,2],[2,2]])
sage: skp2 = SkewPartition([[2,1],[2,1]])
sage: skp1.row_lengths(), skp1.column_lengths()
([0, 0], [0, 0])
sage: skp2.row_lengths(), skp2.column_lengths()
([0, 0], [0, 0])
sage: from_row_and_column_length([0,0], [0,0])
...
ValueError: row and column length must be positive
TESTS:
sage: all(from_row_and_column_length(p.row_lengths(), p.column_lengths()) == p
... for i in range(8) for p in SkewPartitions(i))
True
EXAMPLES:
sage: from sage.combinat.skew_partition import row_lengths_aux
sage: row_lengths_aux([[5,4,3,1],[3,3,1]])
[2, 1, 2]
sage: row_lengths_aux([[5,4,3,1],[3,1]])
[2, 3]