Subsets

The combinatorial class of the subsets of a finite set. The set can be given as a list or a Set or else as an integer which encodes the set 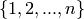. See Subsets for more information and examples.

AUTHORS:

• Mike Hansen: initial version
• Florent Hivert (2009/02/06): doc improvements + new methods

class sage.combinat.subset.SubMultiset_s(s)

Bases: sage.combinat.combinat.CombinatorialClass

The combinatorial class of the sub multisets of s.

EXAMPLES:

sage: S = Subsets([1,2,2,3], submultiset=True)
sage: S._s
[1, 2, 2, 3]

The positions of the unique elements in s are stored in:

sage: S._indices
[0, 1, 3]

and their multiplicities in:

sage: S._multiplicities
[1, 2, 1]
sage: Subsets([1,2,3,3], submultiset=True).cardinality()
12
sage: TestSuite(S).run()

class sage.combinat.subset.SubMultiset_sk(s, k)

Bases: sage.combinat.subset.SubMultiset_s

The combinatorial class of the subsets of size k of a multiset s. Note that each subset is represented by a list of the elements rather than a set since we can have multiplicities (no multiset data structure yet in sage).

EXAMPLES:

sage: S = Subsets([1,2,3,3],2, submultiset=True)
sage: S._k
2
sage: S.cardinality()
4
sage: S.first()
[1, 2]
sage: S.last()
[3, 3]
sage: [sub for sub in S]
[[1, 2], [1, 3], [2, 3], [3, 3]]
sage: TestSuite(S).run()

sage.combinat.subset.Subsets(s, k=None, submultiset=False)

Returns the combinatorial class of the subsets of the finite set s. The set can be given as a list, Set or any iterable convertible to a set. It can alternatively be given a non-negative integer which encode the set 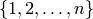(i.e. the Sage range(1,s+1)).

A second optional parameter k can be given. In this case, Subsets returns the combinatorial class of subsets of s of size k.

Finally the option submultiset allows one to deal with sets with repeated elements usually called multisets.

EXAMPLES:

sage: S = Subsets([1, 2, 3]); S
Subsets of {1, 2, 3}
sage: S.cardinality()
8
sage: S.first()
{}
sage: S.last()
{1, 2, 3}
sage: S.random_element()
{2}
sage: S.list()
[{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}]

Here is the same example where the set is given as an integer:

sage: S = Subsets(3)
sage: S.list()
[{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}]

We demonstrate various the effect of the various options:

sage: S = Subsets(3, 2); S
Subsets of {1, 2, 3} of size 2
sage: S.list()
[{1, 2}, {1, 3}, {2, 3}]

sage: S = Subsets([1, 2, 2], submultiset=True); S
SubMultiset of [1, 2, 2]
sage: S.list()
[[], [1], [2], [1, 2], [2, 2], [1, 2, 2]]

sage: S = Subsets([1, 2, 2, 3], 3, submultiset=True); S
SubMultiset of [1, 2, 2, 3] of size 3
sage: S.list()
[[1, 2, 2], [1, 2, 3], [2, 2, 3]]

class sage.combinat.subset.Subsets_s(s)

Bases: sage.combinat.combinat.CombinatorialClass

cardinality()

Returns the number of subsets of the set s.

This is given by .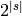

EXAMPLES:

sage: Subsets(Set([1,2,3])).cardinality()
8
sage: Subsets([1,2,3,3]).cardinality()
8
sage: Subsets(3).cardinality()
8

element_class

alias of Set_object_enumerated

first()

Returns the first subset of s. Since we aren’t restricted to subsets of a certain size, this is always the empty set.

EXAMPLES:

sage: Subsets([1,2,3]).first()
{}
sage: Subsets(3).first()
{}

last()

Returns the last subset of s. Since we aren’t restricted to subsets of a certain size, this is always the set s itself.

EXAMPLES:

sage: Subsets([1,2,3]).last()
{1, 2, 3}
sage: Subsets(3).last()
{1, 2, 3}

random_element()

Returns a random element of the class of subsets of s (in other words, a random subset of s).

EXAMPLES:

sage: Subsets(3).random_element()
{2}
sage: Subsets([4,5,6]).random_element()
{5}

rank(sub)

Returns the rank of sub as a subset of s.

EXAMPLES:

sage: Subsets(3).rank([])
0
sage: Subsets(3).rank([1,2])
4
sage: Subsets(3).rank([1,2,3])
7
sage: Subsets(3).rank([2,3,4]) == None
True

unrank(r)

Returns the subset of s that has rank k.

EXAMPLES:

sage: Subsets(3).unrank(0)
{}
sage: Subsets([2,4,5]).unrank(1)
{2}

class sage.combinat.subset.Subsets_sk(s, k)

Bases: sage.combinat.combinat.CombinatorialClass

cardinality()

EXAMPLES:

sage: Subsets(Set([1,2,3]), 2).cardinality()
3
sage: Subsets([1,2,3,3], 2).cardinality()
3
sage: Subsets([1,2,3], 1).cardinality()
3
sage: Subsets([1,2,3], 3).cardinality()
1
sage: Subsets([1,2,3], 0).cardinality()
1
sage: Subsets([1,2,3], 4).cardinality()
0
sage: Subsets(3,2).cardinality()
3
sage: Subsets(3,4).cardinality()
0

element_class

alias of Set_object_enumerated

first()

Returns the first subset of s of size k.

EXAMPLES:

sage: Subsets(Set([1,2,3]), 2).first()
{1, 2}
sage: Subsets([1,2,3,3], 2).first()
{1, 2}
sage: Subsets(3,2).first()
{1, 2}
sage: Subsets(3,4).first()

last()

Returns the last subset of s of size k.

EXAMPLES:

sage: Subsets(Set([1,2,3]), 2).last()
{2, 3}
sage: Subsets([1,2,3,3], 2).last()
{2, 3}
sage: Subsets(3,2).last()
{2, 3}
sage: Subsets(3,4).last()

random_element()

Returns a random element of the class of subsets of s of size k (in other words, a random subset of s of size k).

EXAMPLES:

sage: Subsets(3, 2).random_element()
{1, 2}
sage: Subsets(3,4).random_element() is None
True

rank(sub)

Returns the rank of sub as a subset of s of size k.

EXAMPLES:

sage: Subsets(3,2).rank([1,2])
0
sage: Subsets([2,3,4],2).rank([3,4])
2
sage: Subsets([2,3,4],2).rank([2])
sage: Subsets([2,3,4],4).rank([2,3,4,5])

unrank(r)

Returns the subset of s that has rank k.

EXAMPLES:

sage: Subsets(3,2).unrank(0)
{1, 2}
sage: Subsets([2,4,5],2).unrank(0)
{2, 4}