Set Partitions

A set partition s of a set set is a partition of set, into subsets called parts and represented as a set of sets. By extension, a set partition of a nonnegative integer n is the set partition of the integers from 1 to n. The number of set partitions of n is called the n-th Bell number.

There is a natural integer partition associated with a set partition, that is the non-decreasing sequence of sizes of all its parts.

There is a classical lattice associated with all set partitions of n. The infimum of two set partitions is the set partition obtained by intersecting all the parts of both set partitions. The supremum is obtained by transitive closure of the relation i related to j iff they are in the same part in at least one of the set partitions.

EXAMPLES: There are 5 set partitions of the set 1,2,3.

sage: SetPartitions(3).cardinality()
5

Here is the list of them

sage: SetPartitions(3).list() #random due to the sets
[{{1, 2, 3}}, {{2, 3}, {1}}, {{1, 3}, {2}}, {{1, 2}, {3}}, {{2}, {3}, {1}}]

There are 6 set partitions of 1,2,3,4 whose underlying partition is [2, 1, 1]:

sage: SetPartitions(4, [2,1,1]).list() #random due to the sets
[{{3, 4}, {2}, {1}},
 {{2, 4}, {3}, {1}},
 {{4}, {2, 3}, {1}},
 {{1, 4}, {2}, {3}},
 {{1, 3}, {4}, {2}},
 {{1, 2}, {4}, {3}}]

AUTHORS:

• Mike Hansen
• MuPAD-Combinat developers (for algorithms and design inspiration).

sage.combinat.set_partition.SetPartitions(s, part=None)

An unordered partition of a set is a set of pairwise disjoint nonempty subsets with union and is represented by a sorted list of such subsets.

SetPartitions(s) returns the class of all set partitions of the set s, which can be a set or a string; if a string, each character is considered an element.

SetPartitions(n), where n is an integer, returns the class of all set partitions of the set [1, 2,..., n].

You may specify a second argument k. If k is an integer, SetPartitions returns the class of set partitions into k parts; if it is an integer partition, SetPartitions returns the class of set partitions whose block sizes correspond to that integer partition.

The Bell number 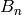, named in honor of Eric Temple Bell, is the number of different partitions of a set with n elements.

EXAMPLES:

sage: S = [1,2,3,4]
sage: SetPartitions(S,2)
Set partitions of [1, 2, 3, 4] with 2 parts
sage: SetPartitions([1,2,3,4], [3,1]).list()
[{{2, 3, 4}, {1}}, {{1, 3, 4}, {2}}, {{3}, {1, 2, 4}}, {{4}, {1, 2, 3}}]
sage: SetPartitions(7, [3,3,1]).cardinality()
70

In strings, repeated letters are considered distinct:

sage: SetPartitions('aabcd').cardinality()
52
sage: SetPartitions('abcde').cardinality()
52

REFERENCES:

• http://en.wikipedia.org/wiki/Partition_of_a_set

class sage.combinat.set_partition.SetPartitions_set(set)

Bases: sage.combinat.set_partition.SetPartitions_setparts

cardinality()

EXAMPLES:

sage: SetPartitions(4).cardinality()
15
sage: bell_number(4)
15

class sage.combinat.set_partition.SetPartitions_setn(set, n)

Bases: sage.combinat.set_partition.SetPartitions_setparts

cardinality()

The Stirling number of the second kind is the number of partitions of a set of size n into k blocks.

EXAMPLES:

sage: SetPartitions(5, 3).cardinality()
25
sage: stirling_number2(5,3)
25

class sage.combinat.set_partition.SetPartitions_setparts(set, parts)

Bases: sage.combinat.combinat.CombinatorialClass

Element

alias of Set_object_enumerated

cardinality()

Returns the number of set partitions of set. This number is given by the n-th Bell number where n is the number of elements in the set.

If a partition or partition length is specified, then count will generate all of the set partitions.

EXAMPLES:

sage: SetPartitions([1,2,3,4]).cardinality()
15
sage: SetPartitions(3).cardinality()
5
sage: SetPartitions(3,2).cardinality()
3
sage: SetPartitions([]).cardinality()
1

sage.combinat.set_partition.inf(s, t)

Returns the infimum of the two set partitions s and t.

EXAMPLES:

sage: sp1 = Set([Set([2,3,4]),Set([1])])
sage: sp2 = Set([Set([1,3]), Set([2,4])])
sage: s = Set([ Set([2,4]), Set([3]), Set([1])]) #{{2, 4}, {3}, {1}}
sage: sage.combinat.set_partition.inf(sp1, sp2) == s
True

sage.combinat.set_partition.less(s, t)

Returns True if s < t otherwise it returns False.

EXAMPLES:

sage: z = SetPartitions(3).list()
sage: sage.combinat.set_partition.less(z[0], z[1])
False
sage: sage.combinat.set_partition.less(z[4], z[1])
True
sage: sage.combinat.set_partition.less(z[4], z[0])
True
sage: sage.combinat.set_partition.less(z[3], z[0])
True
sage: sage.combinat.set_partition.less(z[2], z[0])
True
sage: sage.combinat.set_partition.less(z[1], z[0])
True
sage: sage.combinat.set_partition.less(z[0], z[0])
False

sage.combinat.set_partition.standard_form(sp)

Returns the set partition as a list of lists.

EXAMPLES:

sage: map(sage.combinat.set_partition.standard_form, SetPartitions(4, [2,2]))
[[[3, 4], [1, 2]], [[2, 4], [1, 3]], [[2, 3], [1, 4]]]

sage.combinat.set_partition.sup(s, t)

Returns the supremum of the two set partitions s and t.

EXAMPLES:

sage: sp1 = Set([Set([2,3,4]),Set([1])])
sage: sp2 = Set([Set([1,3]), Set([2,4])])
sage: s = Set([ Set([1,2,3,4]) ])
sage: sage.combinat.set_partition.sup(sp1, sp2) == s
True