Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Combinatorics »

IMPORTANT NOTE (2009/02): The internal functions in this file will be deprecated soon. Please only use them through IntegerListsLex.
Bases: sage.combinat.combinat.CombinatorialClass
A combinatorial class  for integer lists satisfying certain
sum, length, upper/lower bound and regularity constraints. The
purpose of this tool is mostly to provide a Constant Amortized
Time iterator through those lists, in lexicographic order.
for integer lists satisfying certain
sum, length, upper/lower bound and regularity constraints. The
purpose of this tool is mostly to provide a Constant Amortized
Time iterator through those lists, in lexicographic order.
INPUT:
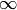
 (or list); defaults to lambda i: 0
(or list); defaults to lambda i: 0 (or list); defaults to lambda i: infinity
(or list); defaults to lambda i: infinity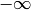 ; defaults to
; defaults to 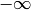
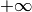 ; defaults to
; defaults to 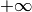
An integer list is a list 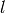 of nonnegative integers, its
parts. The length of
of nonnegative integers, its
parts. The length of 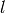 is the number of its parts;
the sum of
is the number of its parts;
the sum of 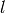 is the sum of its parts.
is the sum of its parts.
Note
Two valid integer lists are considered equivalent if they only differ by trailing zeroes. In this case, only the list with the least number of trailing zeroes will be produced.
The constraints on the lists are as follow:
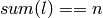
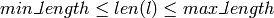
![floor(i) \leq l[i] \leq ceiling(i)](../../_images/math/f807e7cb18d61bcdd2a174c3b6918f70267da11e.png) , for
, for 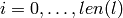
![minSlope \leq l[i+1]-l[i] \leq maxSlope](../../_images/math/cc8f1106246c94ff591190ecfe727e8f3c46c2e0.png) , for
, for 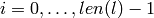
This is a generic low level tool. The interface has been designed with efficiency in mind. It is subject to incompatible changes in the future. More user friendly interfaces are provided by high level tools like Partitions or Compositions.
EXAMPLES:
We create the combinatorial class of lists of length 3 and sum 2:
sage: C = IntegerListsLex(2, length=3)
sage: C
Integer lists of sum 2 satisfying certain constraints
sage: C.cardinality()
6
sage: [p for p in C]
[[2, 0, 0], [1, 1, 0], [1, 0, 1], [0, 2, 0], [0, 1, 1], [0, 0, 2]]
sage: [2, 0, 0] in C
True
sage: [2, 0, 1] in C
False
sage: "a" in C
False
sage: ["a"] in C
False
sage: C.first()
[2, 0, 0]
One can specify lower and upper bound on each part:
sage: list(IntegerListsLex(5, length = 3, floor = [1,2,0], ceiling = [3,2,3]))
[[3, 2, 0], [2, 2, 1], [1, 2, 2]]
Using the slope condition, one can generate integer partitions (but see sage.combinat.partition.Partitions):
sage: list(IntegerListsLex(4, max_slope=0))
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 1, 1, 1]]
This is the list of all partitions of 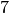 with parts at least
with parts at least  :
:
sage: list(IntegerListsLex(7, max_slope = 0, min_part = 2))
[[7], [5, 2], [4, 3], [3, 2, 2]]
This is the list of all partitions of 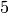 and length at most 3
which are bounded below by [2,1,1]:
and length at most 3
which are bounded below by [2,1,1]:
sage: list(IntegerListsLex(5, max_slope = 0, max_length = 3, floor = [2,1,1]))
[[5], [4, 1], [3, 2], [3, 1, 1], [2, 2, 1]]
Note that [5] is considered valid, because the lower bound constraint only apply to existing positions in the list. To obtain instead the partitions containing [2,1,1], one need to use min_length:
sage: list(IntegerListsLex(5, max_slope = 0, min_length = 3, max_length = 3, floor = [2,1,1]))
[[3, 1, 1], [2, 2, 1]]
This is the list of all partitions of 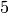 which are contained in [3,2,2]:
which are contained in [3,2,2]:
sage: list(IntegerListsLex(5, max_slope = 0, max_length = 3, ceiling = [3,2,2]))
[[3, 2], [3, 1, 1], [2, 2, 1]]
This is the list of all compositions of 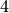 (but see Compositions):
(but see Compositions):
sage: list(IntegerListsLex(4, min_part = 1))
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 3], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
This is the list of all integer vectors of sum 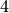 and length
and length 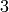 :
:
sage: list(IntegerListsLex(4, length = 3))
[[4, 0, 0], [3, 1, 0], [3, 0, 1], [2, 2, 0], [2, 1, 1], [2, 0, 2], [1, 3, 0], [1, 2, 1], [1, 1, 2], [1, 0, 3], [0, 4, 0], [0, 3, 1], [0, 2, 2], [0, 1, 3], [0, 0, 4]]
There are all the lists of sum 4 and length 4 such that l[i] <= i:
sage: list(IntegerListsLex(4, length=4, ceiling=lambda i: i))
[[0, 1, 2, 1], [0, 1, 1, 2], [0, 1, 0, 3], [0, 0, 2, 2], [0, 0, 1, 3]]
This is the list of all monomials of degree 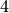 which divide the
monomial
which divide the
monomial 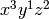 (a monomial being identified with its
exponent vector):
(a monomial being identified with its
exponent vector):
sage: R.<x,y,z> = QQ[]
sage: m = [3,1,2]
sage: def term(exponents):
... return x^exponents[0] * y^exponents[1] * z^exponents[2]
...
sage: list( IntegerListsLex(4, length = len(m), ceiling = m, element_constructor = term) )
[x^3*y, x^3*z, x^2*y*z, x^2*z^2, x*y*z^2]
Note the use of the element_constructor feature.
In general, the complexity of the iteration algorithm is constant
time amortized for each integer list produced. There is one
degenerate case though where the algorithm may run forever without
producing anything. If max_length is 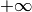 and max_slope
and max_slope 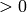 ,
testing whether there exists a valid integer list of sum
,
testing whether there exists a valid integer list of sum  may
be only semi-decidable. In the following example, the algorithm
will enter an infinite loop, because it needs to decide whether
may
be only semi-decidable. In the following example, the algorithm
will enter an infinite loop, because it needs to decide whether
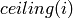 is nonzero for some
is nonzero for some  :
:
sage: list( IntegerListsLex(1, ceiling = lambda i: 0) ) # todo: not implemented
Note
Caveat: counting is done by brute force generation. In some special cases, it would be possible to do better by counting techniques for integral point in polytopes.
Note
Caveat: with the current implementation, the constraints should satisfy the following conditions:
Those conditions are not checked by the algorithm, and the result may be completely incorrect if they are not satisfied:
In the following example, the slope condition is not satisfied by the upper bound on the parts, and [3,3] is erroneously included in the result:
sage: list(IntegerListsLex(6, max_part=3,max_slope=-1))
[[3, 3], [3, 2, 1]]
With some work, this could be fixed without affecting the overall
complexity and efficiency. Also, the generation algorithm could be
extended to deal with non-constant slope constraints and with
negative parts, as well as to accept a range parameter instead of
a single integer for the sum  of the lists (the later was
readily implemented in MuPAD-Combinat). Encouragements,
suggestions, and help are welcome.
of the lists (the later was
readily implemented in MuPAD-Combinat). Encouragements,
suggestions, and help are welcome.
TODO: integrate all remaining tests from http://mupad-combinat.svn.sourceforge.net/viewvc/mupad-combinat/trunk/MuPAD-Combinat/lib/COMBINAT/TEST/MachineIntegerListsLex.tst
TESTS:
sage: g = lambda x: lambda i: x
sage: list(IntegerListsLex(0, floor = g(1), min_slope = 0))
[[]]
sage: list(IntegerListsLex(0, floor = g(1), min_slope = 0, max_slope = 0))
[[]]
sage: list(IntegerListsLex(0, max_length=0, floor = g(1), min_slope = 0, max_slope = 0))
[[]]
sage: list(IntegerListsLex(0, max_length=0, floor = g(0), min_slope = 0, max_slope = 0))
[[]]
sage: list(IntegerListsLex(0, min_part = 1, min_slope = 0))
[[]]
sage: list(IntegerListsLex(1, min_part = 1, min_slope = 0))
[[1]]
sage: list(IntegerListsLex(0, min_length = 1, min_part = 1, min_slope = 0))
[]
sage: list(IntegerListsLex(0, min_length = 1, min_slope = 0))
[[0]]
sage: list(IntegerListsLex(3, max_length=2, ))
[[3], [2, 1], [1, 2], [0, 3]]
sage: partitions = {"min_part": 1, "max_slope": 0}
sage: partitions_min_2 = {"floor": g(2), "max_slope": 0}
sage: compositions = {"min_part": 1}
sage: integer_vectors = lambda l: {"length": l}
sage: lower_monomials = lambda c: {"length": c, "floor": lambda i: c[i]}
sage: upper_monomials = lambda c: {"length": c, "ceiling": lambda i: c[i]}
sage: constraints = { "min_part":1, "min_slope": -1, "max_slope": 0}
sage: list(IntegerListsLex(6, **partitions))
[[6],
[5, 1],
[4, 2],
[4, 1, 1],
[3, 3],
[3, 2, 1],
[3, 1, 1, 1],
[2, 2, 2],
[2, 2, 1, 1],
[2, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]]
sage: list(IntegerListsLex(6, **constraints))
[[6],
[3, 3],
[3, 2, 1],
[2, 2, 2],
[2, 2, 1, 1],
[2, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]]
sage: list(IntegerListsLex(1, **partitions_min_2))
[]
sage: list(IntegerListsLex(2, **partitions_min_2))
[[2]]
sage: list(IntegerListsLex(3, **partitions_min_2))
[[3]]
sage: list(IntegerListsLex(4, **partitions_min_2))
[[4], [2, 2]]
sage: list(IntegerListsLex(5, **partitions_min_2))
[[5], [3, 2]]
sage: list(IntegerListsLex(6, **partitions_min_2))
[[6], [4, 2], [3, 3], [2, 2, 2]]
sage: list(IntegerListsLex(7, **partitions_min_2))
[[7], [5, 2], [4, 3], [3, 2, 2]]
sage: list(IntegerListsLex(9, **partitions_min_2))
[[9], [7, 2], [6, 3], [5, 4], [5, 2, 2], [4, 3, 2], [3, 3, 3], [3, 2, 2, 2]]
sage: list(IntegerListsLex(10, **partitions_min_2))
[[10],
[8, 2],
[7, 3],
[6, 4],
[6, 2, 2],
[5, 5],
[5, 3, 2],
[4, 4, 2],
[4, 3, 3],
[4, 2, 2, 2],
[3, 3, 2, 2],
[2, 2, 2, 2, 2]]
sage: list(IntegerListsLex(4, **compositions))
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 3], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
Returns a list of arguments that can be passed into the pre-existing first,next,is_a, ... functions in this module.
n is currently not included in this list.
EXAMPLES:
sage: C = IntegerListsLex(2, length=3)
sage: C.build_args()
[3,
3,
<function <lambda> at 0x...>,
<function <lambda> at 0x...>,
-Infinity,
+Infinity]
Returns the maximum part that can appear in the 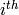 position in any list produced.
position in any list produced.
EXAMPLES:
sage: C = IntegerListsLex(4, length=2, max_part=3)
sage: C.ceiling(0)
3
sage: C = IntegerListsLex(4, length=2, ceiling=[3,2])
sage: C.ceiling(0)
3
sage: C.ceiling(1)
2
Default brute force implementation of count by iteration through all the objects.
Note that this skips the call to _element_constructor, unlike the default implementation from CombinatorialClass
TODO: do the iteration in place to save on copying time
Returns the lexicographically maximal element in this combinatorial class.
EXAMPLES:
sage: C = IntegerListsLex(2, length=3)
sage: C.first()
[2, 0, 0]
Returns the minimum part that can appear in the 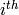 position in any
list produced.
position in any
list produced.
EXAMPLES:
sage: C = IntegerListsLex(4, length=2, min_part=1)
sage: C.floor(0)
1
sage: C = IntegerListsLex(4, length=2, floor=[1,2])
sage: C.floor(0)
1
sage: C.floor(1)
2
Given a composition, returns the lowest regular function N->N below it.
EXAMPLES:
sage: from sage.combinat.integer_list import comp2ceil
sage: f = comp2ceil([2, 1, 1],-1,0)
sage: [f(i) for i in range(10)]
[2, 1, 1, 1, 2, 3, 4, 5, 6, 7]
Given a composition, returns the lowest regular function N->N above it.
EXAMPLES:
sage: from sage.combinat.integer_list import comp2floor
sage: f = comp2floor([2, 1, 1],-1,0)
sage: [f(i) for i in range(10)]
[2, 1, 1, 1, 2, 3, 4, 5, 6, 7]
Returns the lexicographically smallest valid composition of n satisfying the conditions.
Warning
INTERNAL FUNCTION! DO NOT USE DIRECTLY!
Preconditions:
TESTS:
sage: import sage.combinat.integer_list as integer_list
sage: f = lambda l: lambda i: l[i-1]
sage: f([0,1,2,3,4,5])(1)
0
sage: integer_list.first(12, 4, 4, f([0,0,0,0]), f([4,4,4,4]), -1, 1)
[4, 3, 3, 2]
sage: integer_list.first(36, 9, 9, f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -1, 1)
[7, 6, 5, 5, 4, 3, 3, 2, 1]
sage: integer_list.first(25, 9, 9, f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -2, 1)
[7, 6, 5, 4, 2, 1, 0, 0, 0]
sage: integer_list.first(36, 9, 9, f([3,3,3,2,1,4,2,0,0]), f([7,6,5,5,5,5,5,4,4]), -2, 1)
[7, 6, 5, 5, 5, 4, 3, 1, 0]
Returns True if comp meets the constraints imposed by the arguments.
Warning
INTERNAL FUNCTION! DO NOT USE DIRECTLY!
EXAMPLES:
sage: from sage.combinat.integer_list import is_a
sage: IV = IntegerVectors(2,3,min_slope=0)
sage: params = IV._parameters()
sage: all([is_a(iv, *params) for iv in IV])
True
Warning
INTERNAL FUNCTION! DO NOT USE DIRECTLY!
EXAMPLES:
sage: from sage.combinat.integer_list import iterator
sage: IV = IntegerVectors(2,3,min_slope=0)
sage: params = IV._parameters()
sage: list(iterator(2,*params))
[[0, 1, 1], [0, 0, 2]]
Warning
THIS FUNCTION IS DEPRECATED!
Please use IntegersListsLex(...) instead
EXAMPLES:
sage: import sage.combinat.integer_list as integer_list
sage: g = lambda x: lambda i: x
sage: integer_list.list(0,0,infinity,g(1),g(infinity),0,infinity)
[[]]
sage: integer_list.list(0,0,infinity,g(1),g(infinity),0,0)
[[]]
sage: integer_list.list(0, 0, 0, g(1), g(infinity), 0, 0)
[[]]
sage: integer_list.list(0, 0, 0, g(0), g(infinity), 0, 0)
[[]]
sage: integer_list.list(0, 0, infinity, g(1), g(infinity), 0, infinity)
[[]]
sage: integer_list.list(1, 0, infinity, g(1), g(infinity), 0, infinity)
[[1]]
sage: integer_list.list(0, 1, infinity, g(1), g(infinity), 0, infinity)
[]
sage: integer_list.list(0, 1, infinity, g(0), g(infinity), 0, infinity)
[[0]]
sage: integer_list.list(3, 0, 2, g(0), g(infinity), -infinity, infinity)
[[3], [2, 1], [1, 2], [0, 3]]
sage: partitions = (0, infinity, g(0), g(infinity), -infinity, 0)
sage: partitions_min_2 = (0, infinity, g(2), g(infinity), -infinity, 0)
sage: compositions = (0, infinity, g(1), g(infinity), -infinity, infinity)
sage: integer_vectors = lambda l: (l, l, g(0), g(infinity), -infinity, infinity)
sage: lower_monomials = lambda c: (len(c), len(c), g(0), lambda i: c[i], -infinity, infinity)
sage: upper_monomials = lambda c: (len(c), len(c), g(0), lambda i: c[i], -infinity, infinity)
sage: constraints = (0, infinity, g(1), g(infinity), -1, 0)
sage: integer_list.list(6, *partitions)
[[6],
[5, 1],
[4, 2],
[4, 1, 1],
[3, 3],
[3, 2, 1],
[3, 1, 1, 1],
[2, 2, 2],
[2, 2, 1, 1],
[2, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]]
sage: integer_list.list(6, *constraints)
[[6],
[3, 3],
[3, 2, 1],
[2, 2, 2],
[2, 2, 1, 1],
[2, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]]
sage: integer_list.list(1, *partitions_min_2)
[]
sage: integer_list.list(2, *partitions_min_2)
[[2]]
sage: integer_list.list(3, *partitions_min_2)
[[3]]
sage: integer_list.list(4, *partitions_min_2)
[[4], [2, 2]]
sage: integer_list.list(5, *partitions_min_2)
[[5], [3, 2]]
sage: integer_list.list(6, *partitions_min_2)
[[6], [4, 2], [3, 3], [2, 2, 2]]
sage: integer_list.list(7, *partitions_min_2)
[[7], [5, 2], [4, 3], [3, 2, 2]]
sage: integer_list.list(9, *partitions_min_2)
[[9], [7, 2], [6, 3], [5, 4], [5, 2, 2], [4, 3, 2], [3, 3, 3], [3, 2, 2, 2]]
sage: integer_list.list(10, *partitions_min_2)
[[10],
[8, 2],
[7, 3],
[6, 4],
[6, 2, 2],
[5, 5],
[5, 3, 2],
[4, 4, 2],
[4, 3, 3],
[4, 2, 2, 2],
[3, 3, 2, 2],
[2, 2, 2, 2, 2]]
sage: integer_list.list(4, *compositions)
[[4], [3, 1], [2, 2], [2, 1, 1], [1, 3], [1, 2, 1], [1, 1, 2], [1, 1, 1, 1]]
Returns the uppest regular composition below comp
TESTS:
sage: import sage.combinat.integer_list as integer_list
sage: integer_list.lower_regular([4,2,6], -1, 1)
[3, 2, 3]
sage: integer_list.lower_regular([4,2,6], -1, infinity)
[3, 2, 6]
sage: integer_list.lower_regular([1,4,2], -1, 1)
[1, 2, 2]
sage: integer_list.lower_regular([4,2,6,3,7], -2, 1)
[4, 2, 3, 3, 4]
sage: integer_list.lower_regular([4,2,infinity,3,7], -2, 1)
[4, 2, 3, 3, 4]
sage: integer_list.lower_regular([1, infinity, 2], -1, 1)
[1, 2, 2]
sage: integer_list.lower_regular([infinity, 4, 2], -1, 1)
[4, 3, 2]
Returns the next integer list after comp that satisfies the constraints.
Warning
INTERNAL FUNCTION! DO NOT USE DIRECTLY!
EXAMPLES:
sage: from sage.combinat.integer_list import next
sage: IV = IntegerVectors(2,3,min_slope=0)
sage: params = IV._parameters()
sage: next([0,1,1], *params)
[0, 0, 2]
TESTS:
sage: import sage.combinat.integer_list as integer_list
sage: f = lambda l: lambda i: l[i-1]
sage: integer_list.rightmost_pivot([7,6,5,5,4,3,3,2,1], 9, 9, f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -1, 0)
[7, 2]
sage: integer_list.rightmost_pivot([7,6,5,5,4,3,3,2,1], 9, 9,f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -2, 0)
[7, 1]
sage: integer_list.rightmost_pivot([7,6,5,5,4,3,3,2,1], 9, 9,f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -2, 4)
[8, 1]
sage: integer_list.rightmost_pivot([7,6,5,5,4,3,3,2,1], 9, 9,f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -2, 1)
[8, 1]
sage: integer_list.rightmost_pivot([7,6,5,5,5,5,5,4,4], 9, 9,f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -2, 1)
sage: integer_list.rightmost_pivot([3,3,3,2,1,1,0,0,0], 9, 9,f([3,3,3,2,1,1,0,0,0]), f([7,6,5,5,5,5,5,4,4]), -2, 1)
sage: g = lambda x: lambda i: x
sage: integer_list.rightmost_pivot([1],1,1,g(0),g(2),-10, 10)
sage: integer_list.rightmost_pivot([1,2],2,2,g(0),g(2),-10, 10)
sage: integer_list.rightmost_pivot([1,2],2,2,g(1),g(2), -10, 10)
sage: integer_list.rightmost_pivot([1,2],2,3,g(1),g(2), -10, 10)
[2, 1]
sage: integer_list.rightmost_pivot([2,2],2,3,g(2),g(2),-10, 10)
sage: integer_list.rightmost_pivot([2,3],2,3,g(2),g(2),-10,+10)
sage: integer_list.rightmost_pivot([3,2],2,3,g(2),g(2),-10,+10)
sage: integer_list.rightmost_pivot([3,3],2,3,g(2),g(2),-10,+10)
[1, 2]
sage: integer_list.rightmost_pivot([6],1,3,g(0),g(6),-1,0)
[1, 0]
sage: integer_list.rightmost_pivot([6],1,3,g(0),g(6),-2,0)
[1, 0]
sage: integer_list.rightmost_pivot([7,9,8,7],1,5,g(0),g(10),-1,10)
[2, 6]
sage: integer_list.rightmost_pivot([7,9,8,7],1,5,g(5),g(10),-10,10)
[3, 5]
sage: integer_list.rightmost_pivot([7,9,8,7],1,5,g(5),g(10),-1,10)
[2, 6]
sage: integer_list.rightmost_pivot([7,9,8,7],1,5,g(4),g(10),-2,10)
[3, 7]
sage: integer_list.rightmost_pivot([9,8,7],1,4,g(4),g(10),-2,0)
[1, 4]
sage: integer_list.rightmost_pivot([1,3],1,5,lambda i: i,g(10),-10,10)
sage: integer_list.rightmost_pivot([1,4],1,5,lambda i: i,g(10),-10,10)
sage: integer_list.rightmost_pivot([2,4],1,5,lambda i: i,g(10),-10,10)
[1, 1]
Compute a coarse upper bound on the size of a vector satisfying the constraints.
TESTS:
sage: import sage.combinat.integer_list as integer_list
sage: f = lambda x: lambda i: x
sage: integer_list.upper_bound(0,4,f(0), f(1),-infinity,infinity)
4
sage: integer_list.upper_bound(0, infinity, f(0), f(1), -infinity, infinity)
+Infinity
sage: integer_list.upper_bound(0, infinity, f(0), f(1), -infinity, -1)
1
sage: integer_list.upper_bound(0, infinity, f(0), f(5), -infinity, -1)
15
sage: integer_list.upper_bound(0, infinity, f(0), f(5), -infinity, -2)
9
Returns the uppest regular composition above comp.
TESTS:
sage: import sage.combinat.integer_list as integer_list
sage: integer_list.upper_regular([4,2,6],-1,1)
[4, 5, 6]
sage: integer_list.upper_regular([4,2,6],-2, 1)
[4, 5, 6]
sage: integer_list.upper_regular([4,2,6,3,7],-2, 1)
[4, 5, 6, 6, 7]
sage: integer_list.upper_regular([4,2,6,1], -2, 1)
[4, 5, 6, 4]