Direct Sum of Crystals

class sage.combinat.crystals.direct_sum.DirectSumOfCrystals(crystals, **options)

Bases: sage.sets.disjoint_union_enumerated_sets.DisjointUnionEnumeratedSets

Direct sum of crystals.

Given a list of crystals 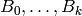of the same Cartan type, one can form the direct sum .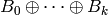

INPUT:

• crystals – a list of crystals of the same Cartan type
• keepkey – a boolean

The option keepkey is by default set to False, assuming that the crystals are all distinct. In this case the elements of the direct sum are just represented by the elements in the crystals 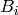. If the crystals are not all distinct, one should set the keepkey option to True. In this case, the elements of the direct sum are represented as tuples 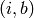where .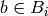

EXAMPLES:

sage: C = CrystalOfLetters(['A',2])
sage: C1 = CrystalOfTableaux(['A',2],shape=[1,1])
sage: B = DirectSumOfCrystals([C,C1])
sage: B.list()
[1, 2, 3, [[1], [2]], [[1], [3]], [[2], [3]]]
sage: [b.f(1) for b in B]
[2, None, None, None, [[2], [3]], None]
sage: B.module_generators
[1, [[1], [2]]]

sage: B = DirectSumOfCrystals([C,C], keepkey=True)
sage: B.list()
[(0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3)]
sage: B.module_generators
[(0, 1), (1, 1)]
sage: b = B( tuple([0,C(1)]) )
sage: b
(0, 1)
sage: b.weight()
(1, 0, 0)

class Element(value, parent)

Bases: sage.structure.element_wrapper.ElementWrapper

A class for elements of direct sums of crystals

e(i)

Returns the action of 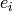on self.

EXAMPLES:

sage: C = CrystalOfLetters(['A',2])
sage: B = DirectSumOfCrystals([C,C], keepkey=True)
sage: [[b, b.e(2)] for b in B]
[[(0, 1), None], [(0, 2), None], [(0, 3), (0, 2)], [(1, 1), None], [(1, 2), None], [(1, 3), (1, 2)]]

epsilon(i)

EXAMPLES:

sage: C = CrystalOfLetters(['A',2])
sage: B = DirectSumOfCrystals([C,C], keepkey=True)
sage: b = B( tuple([0,C(2)]) )
sage: b.epsilon(2)
0

f(i)

Returns the action of 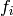on self.

EXAMPLES:

sage: C = CrystalOfLetters(['A',2])
sage: B = DirectSumOfCrystals([C,C], keepkey=True)
sage: [[b,b.f(1)] for b in B]
[[(0, 1), (0, 2)], [(0, 2), None], [(0, 3), None], [(1, 1), (1, 2)], [(1, 2), None], [(1, 3), None]]

phi(i)

EXAMPLES:

sage: C = CrystalOfLetters(['A',2])
sage: B = DirectSumOfCrystals([C,C], keepkey=True)
sage: b = B( tuple([0,C(2)]) )
sage: b.phi(2)
1

weight()

Returns the weight of self.

EXAMPLES:

sage: C = CrystalOfLetters(['A',2])
sage: B = DirectSumOfCrystals([C,C], keepkey=True)
sage: b = B( tuple([0,C(2)]) )
sage: b
(0, 2)
sage: b.weight()
(0, 1, 0)