Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Category Theory »

AUTHORS: - Nicolas Thiery (2008): initial revision - Jason Bandlow & Florent Hivert (2010): Triangular Morphisms
Bases: sage.categories.modules_with_basis.ModuleMorphismByLinearity
A class for diagonal module morphisms.
See ModulesWithBasis.ParentMethods.module_morphism()
Todo:
- implement an optimized _call_ function
- generalize to a mapcoeffs
- generalize to a mapterms
Bases: sage.categories.morphism.Morphism
A class for module morphisms obtained by extending a function by linearity
Returns the action of this morphism on basis elements, as per ModulesWithBasis.HomCategory.ElementMethods.on_basis().
OUTPUT:
EXAMPLES:
sage: X = CombinatorialFreeModule(ZZ, [-2, -1, 1, 2])
sage: Y = CombinatorialFreeModule(ZZ, [1, 2])
sage: phi_on_basis = Y.monomial * abs
sage: phi = sage.categories.modules_with_basis.ModuleMorphismByLinearity(X, on_basis = phi_on_basis, codomain = Y)
sage: x = X.basis()
sage: phi.on_basis()(-2)
B[2]
sage: phi.on_basis() == phi_on_basis
True
Note: could probably be inherited from the categories
Bases: sage.categories.category_types.Category_over_base_ring
The category of modules with a distinguished basis
The elements are represented by expanding them in the distinguished basis. The morphisms are not required to respect the distinguished basis.
EXAMPLES:
sage: ModulesWithBasis(ZZ)
Category of modules with basis over Integer Ring
sage: ModulesWithBasis(ZZ).super_categories()
[Category of modules over Integer Ring]
If the base ring is actually a field, this is a subcategory of the category of abstract vector fields:
sage: ModulesWithBasis(RationalField()).super_categories()
[Category of vector spaces over Rational Field]
Let  and
and 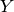 be two modules with basis. We can build
be two modules with basis. We can build 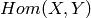 :
:
sage: X = CombinatorialFreeModule(QQ, [1,2]); X.__custom_name = "X"
sage: Y = CombinatorialFreeModule(QQ, [3,4]); Y.__custom_name = "Y"
sage: H = Hom(X, Y); H
Set of Morphisms from X to Y in Category of modules with basis over Rational Field
The simplest morphism is the zero map:
sage: H.zero() # todo: move this test into module once we have an example
Generic morphism:
From: X
To: Y
which we can apply to elements of X:
sage: x = X.monomial(1) + 3 * X.monomial(2)
sage: H.zero()(x)
0
TESTS:
sage: f = H.zero().on_basis()
sage: f(1)
0
sage: f(2)
0
EXAMPLES:
We now construct a more interesting morphism by extending a function by linearity:
sage: phi = H(on_basis = lambda i: Y.monomial(i+2)); phi
Generic morphism:
From: X
To: Y
sage: phi(x)
B[3] + 3*B[4]
We can retrieve the function acting on indices of the basis:
sage: f = phi.on_basis()
sage: f(1), f(2)
(B[3], B[4])
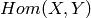 has a natural module structure (except for the zero,
the operations are not yet implemented though). However since the
dimension is not necessarily finite, it is not a module with
basis; but see FiniteDimensionalModulesWithBasis and
GradedModulesWithBasis:
has a natural module structure (except for the zero,
the operations are not yet implemented though). However since the
dimension is not necessarily finite, it is not a module with
basis; but see FiniteDimensionalModulesWithBasis and
GradedModulesWithBasis:
sage: H in ModulesWithBasis(QQ), H in Modules(QQ)
(False, True)
Some more playing around with categories and higher order homsets:
sage: H.category()
Category of hom sets in Category of modules with basis over Rational Field
sage: Hom(H, H).category()
Category of hom sets in Category of modules over Rational Field
# TODO: End(X) is an algebra
TESTS:
sage: TestSuite(ModulesWithBasis(ZZ)).run()
Bases: sage.categories.cartesian_product.CartesianProductsCategory
The category of modules with basis constructed by cartesian products of modules with basis
EXAMPLES:
sage: ModulesWithBasis(QQ).CartesianProducts().extra_super_categories()
[Category of modules with basis over Rational Field]
sage: ModulesWithBasis(QQ).CartesianProducts().super_categories()
[Category of modules with basis over Rational Field, Category of Cartesian products of sets]
Bases: sage.categories.dual.DualObjectsCategory
EXAMPLES:
sage: ModulesWithBasis(ZZ).DualObjects().extra_super_categories()
[Category of modules over Integer Ring]
sage: ModulesWithBasis(QQ).DualObjects().extra_super_categories()
[Category of vector spaces over Rational Field]
Returns the leading coefficient of self.
This is the coefficient of the term whose corresponding basis element is maximal. Note that this may not be the term which actually appears first when self is printed. If the default term ordering is not what is desired, a comparison function, cmp(x,y), can be provided. This should return a negative value if x < y, 0 if x == y and a positive value if x > y.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X")
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + X.monomial(3)
sage: x.leading_coefficient()
1
sage: def cmp(x,y): return y-x
sage: x.leading_coefficient(cmp=cmp)
3
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.leading_coefficient()
-5
Returns the pair (k, c) where c * (the basis elt. indexed by k) is the leading term of self.
‘leading term’ means that the corresponding basis element is
maximal. Note that this may not be the term which actually appears
first when self is printed. If the default term ordering is not
what is desired, a comparison function, cmp(x,y), can be
provided. This should return a negative value if 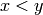 ,
,  if
if
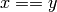 and a positive value if
and a positive value if 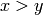 .
.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + 4*X.monomial(3)
sage: x.leading_item()
(3, 4)
sage: def cmp(x,y): return y-x
sage: x.leading_item(cmp=cmp)
(1, 3)
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.leading_item()
([3], -5)
Returns the leading monomial of self.
This is the monomial whose corresponding basis element is maximal. Note that this may not be the term which actually appears first when self is printed. If the default term ordering is not what is desired, a comparison function, cmp(x,y), can be provided. This should return a negative value if x < y, 0 if x == y and a positive value if x > y.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + X.monomial(3)
sage: x.leading_monomial()
B[3]
sage: def cmp(x,y): return y-x
sage: x.leading_monomial(cmp=cmp)
B[1]
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.leading_monomial()
s[3]
Returns the maximal element of the support of self. Note that this may not be the term which actually appears first when self is printed.
If the default ordering of the basis elements is not what is
desired, a comparison function, cmp(x,y), can be provided.
This should return a negative value if 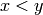 ,
,  if
if 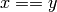 and a positive value if
and a positive value if 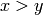 .
.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + 4*X.monomial(3)
sage: x.leading_support()
3
sage: def cmp(x,y): return y-x
sage: x.leading_support(cmp=cmp)
1
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.leading_support()
[3]
Returns the leading term of self.
This is the term whose corresponding basis element is maximal. Note that this may not be the term which actually appears first when self is printed. If the default term ordering is not what is desired, a comparison function, cmp(x,y), can be provided. This should return a negative value if x < y, 0 if x == y and a positive value if x > y.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + X.monomial(3)
sage: x.leading_term()
B[3]
sage: def cmp(x,y): return y-x
sage: x.leading_term(cmp=cmp)
3*B[1]
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.leading_term()
-5*s[3]
Mapping a function on coefficients
INPUT:
- f – an endofunction on the coefficient ring of the free module
Returns a new element of self.parent() obtained by applying the
function  to all of the coefficients of self.
to all of the coefficients of self.
EXAMPLES:
sage: F = CombinatorialFreeModule(QQ, ['a','b','c'])
sage: B = F.basis()
sage: f = B['a'] - 3*B['c']
sage: f.map_coefficients(lambda x: x+5)
6*B['a'] + 2*B['c']
Killed coefficients are handled properly:
sage: f.map_coefficients(lambda x: 0)
0
sage: list(f.map_coefficients(lambda x: 0))
[]
sage: s = SFASchur(QQ)
sage: a = s([2,1])+2*s([3,2])
sage: a.map_coefficients(lambda x: x*2)
2*s[2, 1] + 4*s[3, 2]
Mapping a function on items
INPUT:
- f – a function mapping pairs (index, coeff) to other such pairs
Returns a new element of self.parent() obtained by
applying the function  to all items (index,coeff) of
self.
to all items (index,coeff) of
self.
EXAMPLES:
sage: B = CombinatorialFreeModule(ZZ, [-1, 0, 1])
sage: x = B.an_element(); x
2*B[-1] + 2*B[0] + 3*B[1]
sage: x.map_item(lambda i, c: (-i, 2*c))
6*B[-1] + 4*B[0] + 4*B[1]
f needs not be injective:
sage: x.map_item(lambda i, c: (1, 2*c))
14*B[1]
sage: s = SFASchur(QQ)
sage: f = lambda m,c: (m.conjugate(), 2*c)
sage: a = s([2,1]) + s([1,1,1])
sage: a.map_item(f)
2*s[2, 1] + 2*s[3]
The following methods are deprecated:
sage: a.map_term(f)
doctest:1: DeprecationWarning: (Since Sage Version 4.4.2) map_term is deprecated. Please use map_item instead.
2*s[2, 1] + 2*s[3]
sage: a.map_mc(f)
doctest:1: DeprecationWarning: (Since Sage Version 4.4.2) map_mc is deprecated. Please use map_item instead.
2*s[2, 1] + 2*s[3]
Mapping a function on items
INPUT:
- f – a function mapping pairs (index, coeff) to other such pairs
Returns a new element of self.parent() obtained by
applying the function  to all items (index,coeff) of
self.
to all items (index,coeff) of
self.
EXAMPLES:
sage: B = CombinatorialFreeModule(ZZ, [-1, 0, 1])
sage: x = B.an_element(); x
2*B[-1] + 2*B[0] + 3*B[1]
sage: x.map_item(lambda i, c: (-i, 2*c))
6*B[-1] + 4*B[0] + 4*B[1]
f needs not be injective:
sage: x.map_item(lambda i, c: (1, 2*c))
14*B[1]
sage: s = SFASchur(QQ)
sage: f = lambda m,c: (m.conjugate(), 2*c)
sage: a = s([2,1]) + s([1,1,1])
sage: a.map_item(f)
2*s[2, 1] + 2*s[3]
The following methods are deprecated:
sage: a.map_term(f)
doctest:1: DeprecationWarning: (Since Sage Version 4.4.2) map_term is deprecated. Please use map_item instead.
2*s[2, 1] + 2*s[3]
sage: a.map_mc(f)
doctest:1: DeprecationWarning: (Since Sage Version 4.4.2) map_mc is deprecated. Please use map_item instead.
2*s[2, 1] + 2*s[3]
Mapping a function on the support
INPUT:
- f – an endofunction on the indices of the free module
Returns a new element of self.parent() obtained by
applying the function  to all of the objects indexing
the basis elements.
to all of the objects indexing
the basis elements.
EXAMPLES:
sage: B = CombinatorialFreeModule(ZZ, [-1, 0, 1])
sage: x = B.an_element(); x
2*B[-1] + 2*B[0] + 3*B[1]
sage: x.map_support(lambda i: -i)
3*B[-1] + 2*B[0] + 2*B[1]
f needs not be injective:
sage: x.map_support(lambda i: 1)
7*B[1]
sage: s = SFASchur(QQ)
sage: a = s([2,1])+2*s([3,2])
sage: a.map_support(lambda x: x.conjugate())
s[2, 1] + 2*s[2, 2, 1]
TESTS:
sage: B.zero() # This actually failed at some point!!! See #8890
0
Mapping a function on items
INPUT:
- f – a function mapping pairs (index, coeff) to other such pairs
Returns a new element of self.parent() obtained by
applying the function  to all items (index,coeff) of
self.
to all items (index,coeff) of
self.
EXAMPLES:
sage: B = CombinatorialFreeModule(ZZ, [-1, 0, 1])
sage: x = B.an_element(); x
2*B[-1] + 2*B[0] + 3*B[1]
sage: x.map_item(lambda i, c: (-i, 2*c))
6*B[-1] + 4*B[0] + 4*B[1]
f needs not be injective:
sage: x.map_item(lambda i, c: (1, 2*c))
14*B[1]
sage: s = SFASchur(QQ)
sage: f = lambda m,c: (m.conjugate(), 2*c)
sage: a = s([2,1]) + s([1,1,1])
sage: a.map_item(f)
2*s[2, 1] + 2*s[3]
The following methods are deprecated:
sage: a.map_term(f)
doctest:1: DeprecationWarning: (Since Sage Version 4.4.2) map_term is deprecated. Please use map_item instead.
2*s[2, 1] + 2*s[3]
sage: a.map_mc(f)
doctest:1: DeprecationWarning: (Since Sage Version 4.4.2) map_mc is deprecated. Please use map_item instead.
2*s[2, 1] + 2*s[3]
INPUT:
- self - a monomial, possibly with coefficient
Returns the support of self.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1,2,3,4]); X.rename("X")
sage: X.monomial(2).support_of_term()
2
sage: X.term(3, 2).support_of_term()
3
An exception is raised if self has more than one term:
sage: (X.monomial(2) + X.monomial(3)).support_of_term()
...
ValueError: B[2] + B[3] is not a single term
Returns the tensor product of its arguments, as an element of the tensor product of the parents of those elements.
EXAMPLES:
sage: C = AlgebrasWithBasis(QQ)
sage: A = C.example()
sage: (a,b,c) = A.algebra_generators()
sage: a.tensor(b, c)
B[word: a] # B[word: b] # B[word: c]
FIXME: is this a policy that we want to enforce on all parents?
Returns the trailing coefficient of self.
This is the coefficient of the monomial whose corresponding basis element is minimal. Note that this may not be the term which actually appears last when self is printed. If the default term ordering is not what is desired, a comparison function cmp(x,y), can be provided. This should return a negative value if x < y, 0 if x == y and a positive value if x > y.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + X.monomial(3)
sage: x.trailing_coefficient()
3
sage: def cmp(x,y): return y-x
sage: x.trailing_coefficient(cmp=cmp)
1
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.trailing_coefficient()
2
Returns the pair (c, k) where c*self.parent().monomial(k) is the trailing term of self.
This is the monomial whose corresponding basis element is minimal. Note that this may not be the term which actually appears last when self is printed. If the default term ordering is not what is desired, a comparison function cmp(x,y), can be provided. This should return a negative value if x < y, 0 if x == y and a positive value if x > y.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + X.monomial(3)
sage: x.trailing_item()
(1, 3)
sage: def cmp(x,y): return y-x
sage: x.trailing_item(cmp=cmp)
(3, 1)
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.trailing_item()
([1], 2)
Returns the trailing monomial of self.
This is the monomial whose corresponding basis element is minimal. Note that this may not be the term which actually appears last when self is printed. If the default term ordering is not what is desired, a comparison function cmp(x,y), can be provided. This should return a negative value if x < y, 0 if x == y and a positive value if x > y.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + X.monomial(3)
sage: x.trailing_monomial()
B[1]
sage: def cmp(x,y): return y-x
sage: x.trailing_monomial(cmp=cmp)
B[3]
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.trailing_monomial()
s[1]
Returns the minimal element of the support of self. Note that this may not be the term which actually appears last when self is printed.
If the default ordering of the basis elements is not what is
desired, a comparison function, cmp(x,y), can be provided.
This should return a negative value if 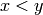 ,
,  if
if 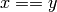 and a positive value if
and a positive value if 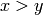 .
.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + 4*X.monomial(3)
sage: x.trailing_support()
1
sage: def cmp(x,y): return y-x
sage: x.trailing_support(cmp=cmp)
3
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.trailing_support()
[1]
Returns the trailing term of self.
This is the term whose corresponding basis element is minimal. Note that this may not be the term which actually appears last when self is printed. If the default term ordering is not what is desired, a comparison function cmp(x,y), can be provided. This should return a negative value if x < y, 0 if x == y and a positive value if x > y.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: x = 3*X.monomial(1) + 2*X.monomial(2) + X.monomial(3)
sage: x.trailing_term()
3*B[1]
sage: def cmp(x,y): return y-x
sage: x.trailing_term(cmp=cmp)
B[3]
sage: s = SymmetricFunctions(QQ).schur()
sage: f = 2*s[1] + 3*s[2,1] - 5*s[3]
sage: f.trailing_term()
2*s[1]
Bases: sage.categories.category.HomCategory
The category of homomorphisms sets Hom(X,Y) for X, Y modules with basis
Constructs morphisms by linearity
Constructs morphisms 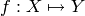 by linearity on a basis
by linearity on a basis
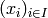 of
of  .
.
INPUT:
self - a parent
in ModulesWithBasis(R), with basis
indexed by
codomain - the codomain
of
: defaults to f.codomain() if the later is defined
zero - the zero of the codomain; defaults to codomain.zero() or 0 if codomain is not specified
position - a non negative integer; defaults to 0
on_basis - a function
which accepts elements of
as position-th argument and returns elements of
diagonal - a function
from
to
- triangular - “upper” or “lower” or None
- “upper”: if the
of the image of
is
, or
- “lower”: if the
of the image of
is
.
category - a category. By default, this is ModulesWithBasis(R) if
is in this category, and otherwise this lets
decide
Exactly one of on_basis and diagonal options should be specified.
With the on_basis option, this returns a function 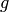 obtained by extending
obtained by extending  by linearity on the position-th
positional argument. For example, for position == 1 and a
ternary function
by linearity on the position-th
positional argument. For example, for position == 1 and a
ternary function  , one has:
, one has:
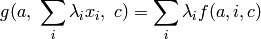
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1,2,3]); X.rename("X")
sage: Y = CombinatorialFreeModule(QQ, [1,2,3,4]); Y.rename("Y")
sage: phi = X.module_morphism(lambda i: Y.monomial(i) + 2*Y.monomial(i+1), codomain = Y)
sage: phi
Generic morphism:
From: X
To: Y
sage: x = X.basis()
sage: phi(x[1] + x[3])
B[1] + 2*B[2] + B[3] + 2*B[4]
With the diagonal argument, this returns the module morphism 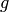 such that:
such that:
This assumes that the respective bases  and
and  of
of  and
and 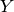 have the same index set
have the same index set  .
.
With triangular = upper, the constructed module
morphism is assumed to be upper triangular; that is its
matrix in the distinguished basis of  and
and 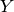 would be
upper triangular with invertible elements on its
diagonal. This is used to compute preimages and
inverting the morphism:
would be
upper triangular with invertible elements on its
diagonal. This is used to compute preimages and
inverting the morphism:
sage: I = range(1,200)
sage: X = CombinatorialFreeModule(QQ, I); X.rename("X"); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, I); Y.rename("Y"); y = Y.basis()
sage: f = Y.sum_of_monomials * divisors
sage: phi = X.module_morphism(f, triangular="upper", codomain = Y)
sage: phi(x[2])
B[1] + B[2]
sage: phi(x[6])
B[1] + B[2] + B[3] + B[6]
sage: phi(x[30])
B[1] + B[2] + B[3] + B[5] + B[6] + B[10] + B[15] + B[30]
sage: phi.preimage(y[2])
-B[1] + B[2]
sage: phi.preimage(y[6])
B[1] - B[2] - B[3] + B[6]
sage: phi.preimage(y[30])
-B[1] + B[2] + B[3] + B[5] - B[6] - B[10] - B[15] + B[30]
sage: (phi^-1)(y[30])
-B[1] + B[2] + B[3] + B[5] - B[6] - B[10] - B[15] + B[30]
For details and further optional arguments, see sage.categories.modules_with_basis.TriangularModuleMorphism.
Caveat: the returned element is in Hom(codomain, domain, category). This is only correct for unary functions.
Todo: should codomain be self by default in the diagonal and triangular cases?
Returns the tensor product of the parents
EXAMPLES:
sage: C = AlgebrasWithBasis(QQ)
sage: A = C.example(); A.rename("A")
sage: A.tensor(A,A)
A # A # A
Bases: sage.categories.tensor.TensorProductsCategory
The category of modules with basis constructed by tensor product of modules with basis
EXAMPLES:
sage: ModulesWithBasis(QQ).TensorProducts().extra_super_categories()
[Category of modules with basis over Rational Field]
sage: ModulesWithBasis(QQ).TensorProducts().super_categories()
[Category of modules with basis over Rational Field]
Returns whether this category is abelian
This is the case if and only if the base ring is a field.
EXAMPLES:
sage: ModulesWithBasis(QQ).is_abelian()
True
sage: ModulesWithBasis(ZZ).is_abelian()
False
EXAMPLES:
sage: ModulesWithBasis(QQ).super_categories()
[Category of vector spaces over Rational Field]
sage: ModulesWithBasis(ZZ).super_categories()
[Category of modules over Integer Ring]
Bases: sage.structure.sage_object.SageObject
A class for point wise inverse functions
EXAMPLES:
sage: from sage.categories.modules_with_basis import PointwiseInverseFunction
sage: f = PointwiseInverseFunction(factorial)
sage: f(0), f(1), f(2), f(3)
(1, 1, 1/2, 1/6)
TESTS:
sage: from sage.categories.modules_with_basis import PointwiseInverseFunction
sage: g = PointwiseInverseFunction(operator.mul)
sage: g.pointwise_inverse() is operator.mul
True
Bases: sage.categories.modules_with_basis.ModuleMorphismByLinearity
A class for triangular module morphisms; that is module morphisms
from  to
to 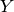 whose matrix in the distinguished basis of
whose matrix in the distinguished basis of  and
and
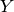 would be upper triangular with invertible elements on its
diagonal.
would be upper triangular with invertible elements on its
diagonal.
See ModulesWithBasis.ParentMethods.module_morphism()
INPUT:
domain - a module with basis
codomain - a module with basis
(defaults to
)
on_basis - a function from the index set of the basis of
to the elements of
which describes the morphism
unitriangular - boolean (default: False)
- triangular - “upper” or “lower” (default: “upper”)
- “upper”: if the
of the image of
is
, or
- “lower”: if the
of the image of
is
.
cmp - an optional comparison function on the index set
of the basis of the codomain.
invertible - should be set to True if self is invertible. Automatically set to True if the domain and codomain share the same indexing set
inverse_on_support - compute the inverse on the support if the codomain and domain have different index sets. see assumptions below
Assumptions:
and
have the same base ring
- let
and
be the respective index sets of the basis of
and
. Either
or inverse_on_support is a function
with the following property: for any
,
should return an
such that the leading term of on_basis(i) is
if there exists such a
or None if not.
OUTPUT:
The triangular module morphism fromto
which maps
to
and is extended by linearity.
EXAMPLES:
sage: I = range(1,200)
sage: X = CombinatorialFreeModule(QQ, I); X.rename("X"); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, I); Y.rename("Y"); y = Y.basis()
sage: f = Y.sum_of_monomials * divisors
sage: phi = X.module_morphism(f, triangular="upper", unitriangular = True, codomain = Y)
sage: phi(x[2])
B[1] + B[2]
sage: phi(x[6])
B[1] + B[2] + B[3] + B[6]
sage: phi(x[30])
B[1] + B[2] + B[3] + B[5] + B[6] + B[10] + B[15] + B[30]
sage: phi.preimage(y[2])
-B[1] + B[2]
sage: phi.preimage(y[6])
B[1] - B[2] - B[3] + B[6]
sage: phi.preimage(y[30])
-B[1] + B[2] + B[3] + B[5] - B[6] - B[10] - B[15] + B[30]
sage: (phi^-1)(y[30])
-B[1] + B[2] + B[3] + B[5] - B[6] - B[10] - B[15] + B[30]
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); X.rename("X"); x = X.basis()
sage: def ut(i): return sum(j*x[j] for j in range(i,4))
sage: phi = X.module_morphism(ut, triangular="lower", codomain = X)
sage: phi(x[2])
2*B[2] + 3*B[3]
sage: phi.preimage(x[2])
1/2*B[2] - 1/2*B[3]
sage: phi(phi.preimage(x[2]))
B[2]
sage: X = CombinatorialFreeModule(QQ, [1,2,3]); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, [1,2,3,4,5]); y = Y.basis()
sage: uut = lambda i: sum( y[j] for j in range(i+1,6) )
sage: phi = X.module_morphism(uut, codomain = Y,
... triangular=True, unitriangular=True,
... inverse_on_support=lambda i: i-1 if i in [2,3,4] else None)
sage: phi(x[2])
B[3] + B[4] + B[5]
sage: phi.preimage(y[3])
B[2] - B[3]
Returns a projection on the co-kernel of self
INPUT:
- `category` -- the category of the result.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1,2,3]); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, [1,2,3,4,5]); y = Y.basis()
sage: uut = lambda i: sum( y[j] for j in range(i+1,6) ) # uni-upper
sage: phi = X.module_morphism(uut, triangular=True, codomain = Y,
... inverse_on_support=lambda i: i-1 if i in [2,3,4] else None)
sage: phipro = phi.co_kernel_projection()
sage: phipro(y[1] + y[2])
B[1]
sage: all(phipro(phi(x)).is_zero() for x in X.basis())
True
sage: phipro(y[1])
B[1]
sage: phipro(y[4])
-B[5]
sage: phipro(y[5])
B[5]
Reduces element w.r.t image of self
Suppose that self is a morphism from  to
to 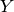 . Then for any
. Then for any
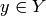 , the calls self.co_reduced(y) returns a normal form for
, the calls self.co_reduced(y) returns a normal form for
 in the quotient
in the quotient 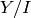 where
where  is the image of self.
is the image of self.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, [1, 2, 3]); y = Y.basis()
sage: uut = lambda i: sum( y[j] for j in range(i,4) ) # uni-upper
sage: phi = X.module_morphism(uut, triangular=True, codomain = Y)
sage: phi.co_reduced(y[1] + y[2])
0
Returns the image of f by the inverse of self.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, [1, 2, 3]); y = Y.basis()
sage: uut = lambda i: sum( y[j] for j in range(i,4) ) # uni-upper
sage: phi = X.module_morphism(uut, triangular=True, codomain = Y)
sage: phi.preimage(y[1] + y[2])
B[1] - B[3]
sage: X = CombinatorialFreeModule(QQ, [1, 2, 3]); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, [1, 2, 3, 4]); y = Y.basis()
sage: uut = lambda i: sum( y[j] for j in range(i,5) ) # uni-upper
sage: phi = X.module_morphism(uut, triangular=True, codomain = Y)
sage: phi.preimage(y[1] + y[2])
B[1] - B[3]
sage: X = CombinatorialFreeModule(QQ, [1,2,3]); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, [1,2,3,4,5]); y = Y.basis()
sage: uut = lambda i: sum( y[j] for j in range(i+1,6) ) # uni-upper
sage: phi = X.module_morphism(uut, triangular=True, codomain = Y,
... inverse_on_support=lambda i: i-1 if i in [2,3,4] else None)
sage: phi.preimage(y[2] + y[3])
B[1] - B[3]
sage: phi(phi.preimage(y[2] + y[3])) == y[2] + y[3]
True
sage: el = x[1] + 3*x[2] + 2*x[3]
sage: phi.preimage(phi(el)) == el
True
sage: phi = X.module_morphism(uut, triangular=True, codomain = Y,
... inverse_on_support=lambda i: i-1 if i in [2,3,4] else None)
sage: phi.preimage(y[1])
...
ValueError: B[1] is not in the image of Generic morphism:
From: X
To: Free module generated by {1, 2, 3, 4, 5} over Rational Field
Returns the section (partial inverse) of self.
Returns a partial triangular morphism which is a section of self. The section morphism raise a ValueError if asked to apply on an element which is not in the image of self.
EXAMPLES:
sage: X = CombinatorialFreeModule(QQ, [1,2,3]); x = X.basis()
sage: Y = CombinatorialFreeModule(QQ, [1,2,3,4,5]); y = Y.basis()
sage: uut = lambda i: sum( y[j] for j in range(i+1,6) ) # uni-upper
sage: phi = X.module_morphism(uut, triangular=True, codomain = Y,
... inverse_on_support=lambda i: i-1 if i in [2,3,4] else None)
sage: ~phi
...
ValueError: Non invertible morphism
sage: phiinv = phi.section()
sage: map(phiinv*phi, X.basis().list()) == X.basis().list()
True
sage: phiinv(Y.basis()[1])
...
ValueError: B[1] is not in the image of Generic morphism:
From: X
To: Free module generated by {1, 2, 3, 4, 5} over Rational Field
Returns the function (...) -> 1 / f(...)
EXAMPLES:
sage: from sage.categories.modules_with_basis import pointwise_inverse_function
sage: def f(x): return x
...
sage: g = pointwise_inverse_function(f)
sage: g(1), g(2), g(3)
(1, 1/2, 1/3)
pointwise_inverse_function is an involution:
sage: f is pointwise_inverse_function(g)
True
Todo: this has nothing to do here!!! Should there be a library for pointwise operations on functions somewhere in Sage?