Modules

class sage.categories.modules.Modules(base, name=None)

Bases: sage.categories.category_types.Category_module

The category of all modules over a base ring

A -module is a left and right -module over a commutative ring such that:

INPUT:

• base_ring – a ring
• dispatch – a boolean (for internal use; default: True)

When the base ring is a field, the category of vector spaces is returned instead (unless dispatch == False).

EXAMPLES:

sage: Modules(IntegerRing())
Category of modules over Integer Ring
sage: Modules(RationalField())
Category of vector spaces over Rational Field

sage: Modules(Integers(9))
Category of modules over Ring of integers modulo 9

sage: Modules(Integers(9)).super_categories()
[Category of bimodules over Ring of integers modulo 9 on the left and Ring of integers modulo 9 on the right]
sage: Modules(Integers(9)).all_super_categories()
[Category of modules over Ring of integers modulo 9,
 Category of bimodules over Ring of integers modulo 9 on the left and Ring of integers modulo 9 on the right,
 Category of left modules over Ring of integers modulo 9,
 Category of right modules over Ring of integers modulo 9,
 Category of commutative additive groups,
 Category of commutative additive monoids,
 Category of commutative additive semigroups,
 Category of additive magmas,
 Category of sets,
 Category of sets with partial maps,
 Category of objects]

sage: Modules(ZZ).super_categories()
[Category of bimodules over Integer Ring on the left and Integer Ring on the right]

sage: Modules == RingModules
True

sage: Modules(ZZ[x]).is_abelian()   # see #6081
True

TESTS:

sage: TestSuite(Modules(ZZ)).run()

TODO:

• Implement a FreeModules(R) category, when so prompted by a concrete use case

class ElementMethods

class Modules.EndCategory(category, name=None)

Bases: sage.categories.modules.Modules.HomCategory

The category of endomorphisms sets 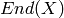for module (this is not used yet)

extra_super_categories()

EXAMPLES:

sage: Hom(ZZ^3, ZZ^3).category().extra_super_categories() # todo: not implemented
[Category of algebras over Integer Ring]

class Modules.HomCategory(category, name=None)

Bases: sage.categories.category.HomCategory

The category of homomorphisms sets 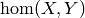for , 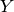modules

ParentMethods

alias of HomCategory.ParentMethods

extra_super_categories()

EXAMPLES:

sage: Modules(ZZ).hom_category().extra_super_categories()
[Category of modules over Integer Ring]

class Modules.ParentMethods

Modules.super_categories(*args, **kwds)

EXAMPLES:

sage: Modules(ZZ).super_categories()
[Category of bimodules over Integer Ring on the left and Integer Ring on the right]

Nota bene:

sage: Modules(QQ)
Category of vector spaces over Rational Field
sage: Modules(QQ).super_categories()
[Category of modules over Rational Field]