Dual functorial construction

AUTHORS:

• Nicolas M. Thiery (2009-2010): initial revision

class sage.categories.dual.DualFunctor

Bases: sage.categories.covariant_functorial_construction.CovariantFunctorialConstruction

A singleton class for the dual functor

sage.categories.dual.DualObjects(self)

Returns the category of duals of objects of self.

INPUT:

• self – a subcategory of vector spaces over some base ring

The dual of a vector space 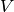is the space consisting of all linear functionals on 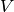(http://en.wikipedia.org/wiki/Dual_space). Additional structure on 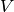can endow its dual with additional structure; e.g. if 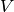is an algebra, then its dual is a coalgebra.

This returns the category of dual of spaces in self endowed with the appropriate additional structure.

See also CovariantFunctorialConstruction.

TODO: add support for graded duals.

EXAMPLES:

sage: VectorSpaces(QQ).DualObjects()
Category of duals of vector spaces over Rational Field

The dual of a vector space is a vector space:

sage: VectorSpaces(QQ).DualObjects().super_categories()
[Category of vector spaces over Rational Field]

The dual of an algebra space is a coalgebra:

sage: Algebras(QQ).DualObjects().super_categories()
[Category of coalgebras over Rational Field, Category of duals of vector spaces over Rational Field]

The dual of a coalgebra space is an algebra:

sage: Coalgebras(QQ).DualObjects().super_categories()
[Category of algebras over Rational Field, Category of duals of vector spaces over Rational Field]

As a shorthand, this category can be accessed with the dual() method:

sage: VectorSpaces(QQ).dual()
Category of duals of vector spaces over Rational Field

TESTS:

sage: C = VectorSpaces(QQ).DualObjects()
sage: C.base_category()
Category of vector spaces over Rational Field
sage: C.super_categories()
[Category of vector spaces over Rational Field]
sage: latex(C)
\mathbf{DualObjects}(\mathbf{VectorSpaces}_{\Bold{Q}})
sage: TestSuite(C).run()

class sage.categories.dual.DualObjectsCategory(category, *args)

Bases: sage.categories.covariant_functorial_construction.CovariantConstructionCategory