Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Category Theory »

Bases: sage.categories.category.Category
The category of (multiplicative) magmas, i.e. sets with a binary operation *.
EXAMPLES:
sage: Magmas()
Category of magmas
sage: Magmas().super_categories()
[Category of sets]
sage: Magmas().all_super_categories()
[Category of magmas, Category of sets, Category of sets with partial maps, Category of objects]
TESTS:
sage: C = Magmas()
sage: TestSuite(C).run(verbose=True)
running ._test_category() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass
Bases: sage.categories.cartesian_product.CartesianProductsCategory
Returns an example of cartesian product of magmas
EXAMPLES:
sage: C = Magmas().CartesianProducts().example(); C
The cartesian product of (Rational Field, Integer Ring, Integer Ring)
sage: C.category()
Category of Cartesian products of monoids
sage: TestSuite(C).run()
EXAMPLES:
sage: Semigroups().CartesianProducts().extra_super_categories()
[Category of semigroups]
sage: Semigroups().CartesianProducts().super_categories()
[Category of semigroups, Category of Cartesian products of magmas]
Test whether self is idempotent.
EXAMPLES:
sage: S = Semigroups().example("free"); S
An example of a semigroup: the free semigroup generated by ('a', 'b', 'c', 'd')
sage: a = S('a')
sage: a^2
'aa'
sage: a.is_idempotent()
False
sage: L = Semigroups().example("leftzero"); L
An example of a semigroup: the left zero semigroup
sage: x = L('x')
sage: x^2
'x'
sage: x.is_idempotent()
True
Returns a table describing the multiplication operation.
Note
The order of the elements in the row and column headings is equal to the order given by the table’s list() method. The association can also be retrieved with the dict() method.
INPUTS:
OUTPUT: The multiplication table as an object of the class OperationTable which defines several methods for manipulating and displaying the table. See the documentation there for full details to supplement the documentation here.
EXAMPLES:
The default is to represent elements as lowercase ASCII letters.
sage: G=CyclicPermutationGroup(5)
sage: G.multiplication_table()
* a b c d e
+----------
a| a b c d e
b| b c d e a
c| c d e a b
d| d e a b c
e| e a b c d
All that is required is that an algebraic structure has a multiplication defined. A LeftRegularBand is an example of a finite semigroup. The names argument allows displaying the elements in different ways.
sage: from sage.categories.examples.finite_semigroups import LeftRegularBand
sage: L=LeftRegularBand(('a','b'))
sage: T=L.multiplication_table(names='digits')
sage: T.column_keys()
('a', 'b', 'ab', 'ba')
sage: T
* 0 1 2 3
+--------
0| 0 2 2 2
1| 3 1 3 3
2| 2 2 2 2
3| 3 3 3 3
Specifying the elements in an alternative order can provide more insight into how the operation behaves.
sage: L=LeftRegularBand(('a','b','c'))
sage: elts = sorted(L.list())
sage: L.multiplication_table(elements=elts)
* a b c d e f g h i j k l m n o
+------------------------------
a| a b c d e b b c c c d d e e e
b| b b c c c b b c c c c c c c c
c| c c c c c c c c c c c c c c c
d| d e e d e e e e e e d d e e e
e| e e e e e e e e e e e e e e e
f| g g h h h f g h i j i j j i j
g| g g h h h g g h h h h h h h h
h| h h h h h h h h h h h h h h h
i| j j j j j i j j i j i j j i j
j| j j j j j j j j j j j j j j j
k| l m m l m n o o n o k l m n o
l| l m m l m m m m m m l l m m m
m| m m m m m m m m m m m m m m m
n| o o o o o n o o n o n o o n o
o| o o o o o o o o o o o o o o o
The elements argument can be used to provide a subset of the elements of the structure. The subset must be closed under the operation. Elements need only be in a form that can be coerced into the set. The names argument can also be used to request that the elements be represented with their usual string representation.
sage: L=LeftRegularBand(('a','b','c'))
sage: elts=['a', 'c', 'ac', 'ca']
sage: L.multiplication_table(names='elements', elements=elts)
* 'a' 'c' 'ac' 'ca'
+--------------------
'a'| 'a' 'ac' 'ac' 'ac'
'c'| 'ca' 'c' 'ca' 'ca'
'ac'| 'ac' 'ac' 'ac' 'ac'
'ca'| 'ca' 'ca' 'ca' 'ca'
The table returned can be manipulated in various ways. See the documentation for OperationTable for more comprehensive documentation.
sage: G=AlternatingGroup(3)
sage: T=G.multiplication_table()
sage: T.column_keys()
((), (1,2,3), (1,3,2))
sage: sorted(T.translation().items())
[('a', ()), ('b', (1,2,3)), ('c', (1,3,2))]
sage: T.change_names(['x', 'y', 'z'])
sage: sorted(T.translation().items())
[('x', ()), ('y', (1,2,3)), ('z', (1,3,2))]
sage: T
* x y z
+------
x| x y z
y| y z x
z| z x y
The binary multiplication of the magma
INPUT:
- x, y: elements of this magma
OUTPUT:
- an element of the magma (the product of x and y)
EXAMPLES:
sage: S = Semigroups().example("free")
sage: x = S('a'); y = S('b')
sage: S.product(x, y)
'ab'
A parent in Magmas() must either implement product() in the parent class or _mul_ in the element class. By default, the addition method on elements x._mul_(y) calls S.product(x,y), and reciprocally.
As a bonus, S.product models the binary function from S to S:
sage: bin = S.product
sage: bin(x,y)
'ab'
Currently, S.product is just a bound method:
sage: bin
<bound method FreeSemigroup_with_category.product of An example of a semigroup: the free semigroup generated by ('a', 'b', 'c', 'd')>
When Sage will support multivariate morphisms, it will be possible, and in fact recommended, to enrich S.product with extra mathematical structure. This will typically be implemented using lazy attributes.:
sage: bin # todo: not implemented
Generic binary morphism:
From: (S x S)
To: S
The binary multiplication of the magma
INPUT:
- x, y: elements of this magma
OUTPUT:
- an element of the magma (the product of x and y)
EXAMPLES:
sage: S = Semigroups().example("free")
sage: x = S('a'); y = S('b')
sage: S.product(x, y)
'ab'
A parent in Magmas() must either implement product() in the parent class or _mul_ in the element class. By default, the addition method on elements x._mul_(y) calls S.product(x,y), and reciprocally.
As a bonus, S.product models the binary function from S to S:
sage: bin = S.product
sage: bin(x,y)
'ab'
Currently, S.product is just a bound method:
sage: bin
<bound method FreeSemigroup_with_category.product of An example of a semigroup: the free semigroup generated by ('a', 'b', 'c', 'd')>
When Sage will support multivariate morphisms, it will be possible, and in fact recommended, to enrich S.product with extra mathematical structure. This will typically be implemented using lazy attributes.:
sage: bin # todo: not implemented
Generic binary morphism:
From: (S x S)
To: S
Bases: sage.categories.subquotients.SubquotientsCategory
The category of sub/quotient magmas.
Let  and
and  be two magmas and
be two magmas and 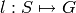 and
and
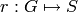 be two maps such that:
be two maps such that:
is the identity of
.
- for any two
the identity
holds.
The category Subquotient implements the product 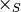 from
from 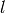 and
and  and the product of
and the product of  .
.
 is supposed to belongs the category
Magmas().Subquotients() and to specify
is supposed to belongs the category
Magmas().Subquotients() and to specify  under the name
S.ambient() and to implement
under the name
S.ambient() and to implement 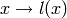 and
and 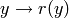 under the names S.lift(x) and S.retract(y).
under the names S.lift(x) and S.retract(y).
EXAMPLES:
sage: Semigroups().Subquotients().all_super_categories()
[Category of subquotients of semigroups, Category of semigroups,
Category of subquotients of magmas, Category of magmas,
Category of subquotients of sets, Category of sets,
Category of sets with partial maps,
Category of objects]
EXAMPLES:
sage: Magmas().super_categories()
[Category of sets]