Finite Permutation Groups

class sage.categories.finite_permutation_groups.FinitePermutationGroups(s=None)

Bases: sage.categories.category.Category

The category of finite permutation groups, i.e. groups concretely represented as groups of permutations acting on a finite set.

EXAMPLES:

sage: FinitePermutationGroups()
Category of finite permutation groups
sage: FinitePermutationGroups().super_categories()
[Category of finite groups]

sage: FinitePermutationGroups().example()
Dihedral group of order 6 as a permutation group

TESTS:

sage: C = FinitePermutationGroups()
sage: TestSuite(C).run(verbose = True)
running ._test_category() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass

sage: G = FinitePermutationGroups().example()
sage: TestSuite(G).run(verbose = True)
running ._test_an_element() . . . pass
running ._test_associativity() . . . pass
running ._test_category() . . . pass
running ._test_elements() . . .
  Running the test suite of self.an_element()
  running ._test_category() . . . pass
  running ._test_eq() . . . pass
  running ._test_not_implemented_methods() . . . pass
  running ._test_pickling() . . . pass
  pass
running ._test_elements_eq() . . . pass
running ._test_enumerated_set_contains() . . . pass
running ._test_enumerated_set_iter_cardinality() . . . pass
running ._test_enumerated_set_iter_list() . . . pass
running ._test_eq() . . . pass
running ._test_inverse() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_one() . . . pass
running ._test_pickling() . . . pass
running ._test_prod() . . . pass
running ._test_some_elements() . . . pass

class ElementMethods

class FinitePermutationGroups.ParentMethods

cycle_index(parent=None)

INPUT:

• self - a permutation group
• parent – a free module with basis indexed by partitions, or behave as such, with a term and sum method (default: the symmetric functions over the rational field in the p basis)

Returns the cycle index of , which is a gadget counting the elements of by cycle type, averaged over the group:

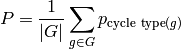
EXAMPLES:

Among the permutations of the symmetric group 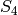, there is the identity, 6 cycles of length 2, 3 products of two cycles of length 2, 8 cycles of length 3, and 6 cycles of length 4:

sage: S4 = SymmetricGroup(4)
sage: P = S4.cycle_index()
sage: 24 * P
p[1, 1, 1, 1] + 6*p[2, 1, 1] + 3*p[2, 2] + 8*p[3, 1] + 6*p[4]

If 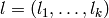is a partition, |G| P[l] is the number of elements of with cycles of length :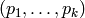

sage: 24 * P[ Partition([3,1]) ]
8

The cycle index plays an important role in the enumeration of objects modulo the action of a group (Polya enumeration), via the use of symmetric functions and plethysms. It is therefore encoded as a symmetric function, expressed in the powersum basis:

sage: P.parent()
Symmetric Function Algebra over Rational Field, Power symmetric functions as basis

This symmetric function can have some nice properties; for example, for the symmetric group 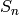, we get the complete symmetric function :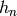

sage: S = SymmetricFunctions(QQ); h = S.h()
sage: h( P )
h[4]

TODO: add some simple examples of Polya enumeration, once it will be easy to expand symmetric functions on any alphabet.

Here are the cycle indices of some permutation groups:

sage: 6 * CyclicPermutationGroup(6).cycle_index()
p[1, 1, 1, 1, 1, 1] + p[2, 2, 2] + 2*p[3, 3] + 2*p[6]

sage: 60 * AlternatingGroup(5).cycle_index()
p[1, 1, 1, 1, 1] + 15*p[2, 2, 1] + 20*p[3, 1, 1] + 24*p[5]

sage: for G in TransitiveGroups(5):               # requires optional database_gap # long time
...       G.cardinality() * G.cycle_index()
p[1, 1, 1, 1, 1] + 4*p[5]
p[1, 1, 1, 1, 1] + 5*p[2, 2, 1] + 4*p[5]
p[1, 1, 1, 1, 1] + 5*p[2, 2, 1] + 10*p[4, 1] + 4*p[5]
p[1, 1, 1, 1, 1] + 15*p[2, 2, 1] + 20*p[3, 1, 1] + 24*p[5]
p[1, 1, 1, 1, 1] + 10*p[2, 1, 1, 1] + 15*p[2, 2, 1] + 20*p[3, 1, 1] + 20*p[3, 2] + 30*p[4, 1] + 24*p[5]

One may specify another parent for the result:

sage: F = CombinatorialFreeModule(QQ, Partitions())
sage: P = CyclicPermutationGroup(6).cycle_index(parent = F)
sage: 6 * P
B[[1, 1, 1, 1, 1, 1]] + B[[2, 2, 2]] + 2*B[[3, 3]] + 2*B[[6]]
sage: P.parent() is F
True

This parent should have a term and sum method:

sage: CyclicPermutationGroup(6).cycle_index(parent = QQ)
Traceback (most recent call last):
  ...
AssertionError: `parent` should be (or behave as) a free module with basis indexed by partitions

REFERENCES:

[Ker1991]

A. Kerber. Algebraic combinatorics via finite group actions, 2.2 p. 70. BI-Wissenschaftsverlag, Mannheim, 1991.

AUTHORS:

• Nicolas Borie and Nicolas M. Thiery

TESTS:

sage: P = PermutationGroup([]); P
Permutation Group with generators [()]
sage: P.cycle_index()
p[1]
sage: P = PermutationGroup([[(1)]]); P
Permutation Group with generators [()]
sage: P.cycle_index()
p[1]

FinitePermutationGroups.example()

Returns an example of finite permutation group, as per Category.example().

EXAMPLES:

sage: G = FinitePermutationGroups().example(); G
Dihedral group of order 6 as a permutation group

FinitePermutationGroups.super_categories(*args, **kwds)

Returns a list of the (immediate) super categories of self.

EXAMPLES:

sage: FinitePermutationGroups().super_categories()
[Category of finite groups]