FiniteSemigroups

class sage.categories.finite_semigroups.FiniteSemigroups(s=None)

Bases: sage.categories.category.Category

The category of (multiplicative) finite semigroups, i.e. enumerated sets with an associative operation *.

EXAMPLES:

sage: FiniteSemigroups()
Category of finite semigroups
sage: FiniteSemigroups().super_categories()
[Category of semigroups, Category of finite enumerated sets]
sage: FiniteSemigroups().all_super_categories()
[Category of finite semigroups,
 Category of semigroups,
 Category of magmas,
 Category of finite enumerated sets,
 Category of enumerated sets,
 Category of sets,
 Category of sets with partial maps,
 Category of objects]
sage: FiniteSemigroups().example()
An example of a finite semigroup: the left regular band generated by ('a', 'b', 'c', 'd')

TESTS:

sage: C = FiniteSemigroups()
sage: TestSuite(C).run(verbose = True)
running ._test_category() . . . pass
running ._test_not_implemented_methods() . . . pass
running ._test_pickling() . . . pass

class ParentMethods

Collection of methods shared by all finite semigroups.

ideal(gens, side='twosided')

Returns the side-sided ideal generated by gens.

INPUT:

- ``gens``: a list (or iterable) of elements of ``self``
- ``side``: [default: "twosided"] "left", "right" or "twosided"

EXAMPLES:

sage: S = FiniteSemigroups().example()
sage: list(S.ideal([S('cab')], side="left"))
['cab', 'dcab', 'adcb', 'acb', 'bdca', 'bca', 'abdc',
'cadb', 'acdb', 'bacd', 'abcd', 'cbad', 'abc', 'acbd',
'dbac', 'dabc', 'cbda', 'bcad', 'cabd', 'dcba',
'bdac', 'cba', 'badc', 'bac', 'cdab', 'dacb', 'dbca',
'cdba', 'adbc', 'bcda']
sage: list(S.ideal([S('cab')], side="right"))
['cab', 'cabd']
sage: list(S.ideal([S('cab')], side="twosided"))
['cab', 'dcab', 'acb', 'adcb', 'acbd', 'bdca', 'bca',
'cabd', 'abdc', 'cadb', 'acdb', 'bacd', 'abcd', 'cbad',
'abc', 'dbac', 'dabc', 'cbda', 'bcad', 'dcba', 'bdac',
'cba', 'cdab', 'bac', 'badc', 'dacb', 'dbca', 'cdba',
'adbc', 'bcda']
sage: list(S.ideal([S('cab')]))
['cab', 'dcab', 'acb', 'adcb', 'acbd', 'bdca', 'bca',
'cabd', 'abdc', 'cadb', 'acdb', 'bacd', 'abcd', 'cbad',
'abc', 'dbac', 'dabc', 'cbda', 'bcad', 'dcba', 'bdac',
'cba', 'cdab', 'bac', 'badc', 'dacb', 'dbca', 'cdba',
'adbc', 'bcda']

idempotents()

Returns the idempotents of the semigroup

EXAMPLES:

sage: S = FiniteSemigroups().example(alphabet=('x','y'))
sage: sorted(S.idempotents())
['x', 'xy', 'y', 'yx']

j_classes(*args, **kwds)

Returns the 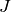-classes of the semigroup.

Two elements and of a monoid are in the same 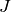-class if divides and divides .

OUTPUT:

All the $J$-classes of self, as a list of lists.

EXAMPLES:

sage: S = FiniteSemigroups().example(alphabet=('a','b', 'c'))
sage: sorted(map(sorted, S.j_classes()))
[['a'], ['ab', 'ba'], ['abc', 'acb', 'bac', 'bca', 'cab', 'cba'], ['ac', 'ca'], ['b'], ['bc', 'cb'], ['c']]

j_classes_of_idempotents(*args, **kwds)

Returns all the idempotents of self, grouped by J-class.

OUTPUT:

a list of lists.

EXAMPLES:

sage: S = FiniteSemigroups().example(alphabet=('a','b', 'c'))
sage: sorted(map(sorted, S.j_classes_of_idempotents()))
[['a'], ['ab', 'ba'], ['abc', 'acb', 'bac', 'bca', 'cab', 'cba'], ['ac', 'ca'], ['b'], ['bc', 'cb'], ['c']]

j_transversal_of_idempotents(*args, **kwds)

Returns a list of one idempotent per regular J-class

EXAMPLES:

sage: S = FiniteSemigroups().example(alphabet=('a','b', 'c'))
sage: sorted(S.j_transversal_of_idempotents())
['a', 'ab', 'ac', 'acb', 'b', 'c', 'cb']

some_elements()

Returns an iterable containing some elements of the semigroup.

EXAMPLES:

sage: S = FiniteSemigroups().example(alphabet=('x','y'))
sage: S.some_elements()
An example of a finite semigroup: the left regular band generated by ('x', 'y')
sage: list(S)
['y', 'x', 'xy', 'yx']

succ_generators(side='twosided')

Returns the the successor function of the side-sided Cayley graph of self.

This is a function that maps an element of self to all the products of x by a generator of this semigroup, where the product is taken on the left, right or both sides.

INPUT:

- ``side``: "left", "right", or "twosided"

FIXME: find a better name for this method FIXME: should we return a set? a family?

EXAMPLES:

sage: S = FiniteSemigroups().example()
sage: S.succ_generators("left" )(S('ca'))
('ac', 'bca', 'ca', 'dca')
sage: S.succ_generators("right")(S('ca'))
('ca', 'cab', 'ca', 'cad')
sage: S.succ_generators("twosided" )(S('ca'))
('ac', 'bca', 'ca', 'dca', 'ca', 'cab', 'ca', 'cad')

FiniteSemigroups.super_categories(*args, **kwds)

Returns a list of the (immediate) super categories of self.

EXAMPLES:

sage: FiniteSemigroups().super_categories()
[Category of semigroups, Category of finite enumerated sets]