Finite Monoids

class sage.categories.finite_monoids.FiniteMonoids(s=None)

Bases: sage.categories.category.Category

The category of finite monoids

EXAMPLES:

sage: FiniteMonoids()
Category of finite monoids
sage: FiniteMonoids().super_categories()
[Category of finite semigroups, Category of monoids]

TESTS:

sage: TestSuite(FiniteMonoids()).run()

class ElementMethods

pseudo_order()

Returns the pair with minimal and 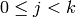such that self^k == self^j.

Note that is uniquely determined.

EXAMPLES:

sage: M = FiniteMonoids().example(); M
An example of a finite multiplicative monoid: the integers modulo 12

sage: x = M(2)
sage: [ x^i for i in range(7) ]
[1, 2, 4, 8, 4, 8, 4]
sage: x.pseudo_order()
[4, 2]

sage: x = M(3)
sage: [ x^i for i in range(7) ]
[1, 3, 9, 3, 9, 3, 9]
sage: x.pseudo_order()
[3, 1]

sage: x = M(4)
sage: [ x^i for i in range(7) ]
[1, 4, 4, 4, 4, 4, 4]
sage: x.pseudo_order()
[2, 1]

sage: x = M(5)
sage: [ x^i for i in range(7) ]
[1, 5, 1, 5, 1, 5, 1]
sage: x.pseudo_order()
[2, 0]

TODO: more appropriate name? see, for example, Jean-Eric Pin’s lecture notes on semigroups.

FiniteMonoids.super_categories(*args, **kwds)

EXAMPLES:

sage: FiniteMonoids().super_categories()
[Category of finite semigroups, Category of monoids]