AUTHORS: - John H. Palmieri (2008-07-30: version 0.9)
This package provides for basic algebra with elements in the mod
 Steenrod algebra. In this package, elements in the
Steenrod algebra are represented, by default, using the Milnor
basis.
Steenrod algebra. In this package, elements in the
Steenrod algebra are represented, by default, using the Milnor
basis.
EXAMPLES:
Basic arithmetic, 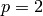 . To construct an element
of the mod 2 Steenrod algebra, use the function
Sq:
. To construct an element
of the mod 2 Steenrod algebra, use the function
Sq:
sage: a = Sq(1,2)
sage: b = Sq(4,1)
sage: z = a + b
sage: z
Sq(1,2) + Sq(4,1)
sage: Sq(4) * Sq(1,2)
Sq(1,1,1) + Sq(2,3) + Sq(5,2)
sage: z**2 # non-negative exponents work as they should
Sq(1,2,1) + Sq(4,1,1)
sage: z**0
Sq(0)
Basic arithmetic, 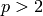 . To construct an element of the mod
. To construct an element of the mod
 Steenrod algebra when
Steenrod algebra when  is odd, you should
first define a Steenrod algebra, using the
SteenrodAlgebra command:
is odd, you should
first define a Steenrod algebra, using the
SteenrodAlgebra command:
sage: SteenrodAlgebra() # 2 is the default prime
mod 2 Steenrod algebra
sage: A3 = SteenrodAlgebra(3)
sage: A3
mod 3 Steenrod algebra
Having done this, the newly created algebra A3 has methods Q and P which construct elements of A3:
sage: c = A3.Q(1,3,6); c
Q_1 Q_3 Q_6
sage: d = A3.P(2,0,1); d
P(2,0,1)
sage: c * d
Q_1 Q_3 Q_6 P(2,0,1)
sage: e = A3.P(3)
sage: d * e
P(5,0,1)
sage: e * d
P(1,1,1) + P(5,0,1)
sage: c * c
0
sage: e ** 3
2 P(1,2)
Note that one can construct an element like c above in one step, without first constructing the algebra:
sage: c = SteenrodAlgebra(3).Q(1,3,6)
sage: c
Q_1 Q_3 Q_6
And of course, you can do similar constructions with the mod 2 Steenrod algebra:
sage: A = SteenrodAlgebra(2); A
mod 2 Steenrod algebra
sage: A.Sq(2,3,5)
Sq(2,3,5)
sage: A.P(2,3,5) # when p=2, P = Sq
Sq(2,3,5)
sage: A.Q(1,4) # when p=2, this gives a product of Milnor primitives
Sq(0,1,0,0,1)
Regardless of the prime, each element has an
excess, and if the element is homogeneous, a
degree. The excess of
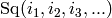 is
is
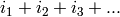 ; when
; when  is odd, the
excess of
is odd, the
excess of
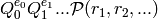 is
is 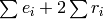 . The excess of a linear
combination of Milnor basis elements is the minimum of the excesses
of those basis elements.
. The excess of a linear
combination of Milnor basis elements is the minimum of the excesses
of those basis elements.
The degree of 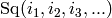 is
is
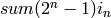 , and when
, and when  is odd, the degree
of
is odd, the degree
of
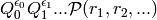 is
is 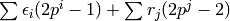 .
The degree of a linear combination of such terms is only defined if
the terms all have the same degree.
.
The degree of a linear combination of such terms is only defined if
the terms all have the same degree.
Here are some simple examples:
sage: z = Sq(1,2) + Sq(4,1)
sage: z.degree()
7
sage: (Sq(0,0,1) + Sq(5,3)).degree()
Element is not homogeneous.
sage: Sq(7,2,1).excess()
10
sage: z.excess()
3
sage: B = SteenrodAlgebra(3)
sage: x = B.Q(1,4)
sage: y = B.P(1,2,3)
sage: x.degree()
166
sage: x.excess()
2
sage: y.excess()
12
Elements have a weight in the May filtration, which
(when 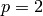 ) is related to the height
function defined by Wall:
) is related to the height
function defined by Wall:
sage: Sq(2,1,5).may_weight()
9
sage: Sq(2,1,5).wall_height()
[2, 3, 2, 1, 1]
sage: b = Sq(4)*Sq(8) + Sq(8)*Sq(4)
sage: b.may_weight()
2
sage: b.wall_height()
[0, 0, 1, 1]
Odd primary May weights:
sage: A5 = SteenrodAlgebra(5)
sage: a = A5.Q(1,2,4)
sage: b = A5.P(1,2,1)
sage: a.may_weight()
10
sage: b.may_weight()
8
sage: (a * b).may_weight()
18
sage: A5.P(0,0,1).may_weight()
3
Since the Steenrod algebra is a Hopf algebra, every element has an antipode.
sage: d = Sq(0,0,1); d
Sq(0,0,1)
sage: d.antipode()
Sq(0,0,1)
sage: Sq(4).antipode()
Sq(1,1) + Sq(4)
sage: (Sq(4) * Sq(2)).antipode()
Sq(6)
sage: SteenrodAlgebra(7).P(3,1).antipode()
P(3,1)
Applying the antipode twice returns the original element:
sage: y = Sq(8)*Sq(4)
sage: y == (y.antipode()).antipode()
True
You can treat elements of the Steenrod algebra like lists of Milnor basis elements:
sage: y = Sq(4) * Sq(1,2); y
Sq(1,1,1) + Sq(2,3) + Sq(5,2)
sage: for m in y: m
Sq(1,1,1)
Sq(2,3)
Sq(5,2)
sage: [(m.degree(),m.excess()) for m in y]
[(11, 3), (11, 5), (11, 7)]
Once you’ve define a Steenrod algebra, the method
pst is another way to define elements of it:
pst(s,t) defines the Margolis element
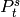 , the basis element
, the basis element
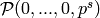 with
with 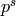 in position
in position
 :
:
sage: A2 = SteenrodAlgebra(2)
sage: Q2 = A2.pst(0,3)
sage: Q2
Sq(0,0,1)
sage: Q2*Q2
0
sage: A2.pst(1,2) == Sq(2)*Sq(4) + Sq(4)*Sq(2)
True
sage: A5 = SteenrodAlgebra(5)
sage: A5.pst(2,2)
P(0,25)
There are a number of different bases available in which to
represent elements of the Steenrod algebra. When 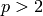 , the
choices are the Milnor basis (‘milnor’) or the Serre-Cartan basis
(‘serre-cartan’ or ‘adem’ or ‘admissible’). When
, the
choices are the Milnor basis (‘milnor’) or the Serre-Cartan basis
(‘serre-cartan’ or ‘adem’ or ‘admissible’). When 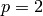 , the
choices are those, along with Wood’s Y basis (‘wood_y’), Wood’s Z
basis (‘wood_z’), Wall’s basis (‘wall’ or ‘wall_long’), Arnon’s A
basis (‘arnon_a’ or ‘arnon_a_long’), Arnon’s C basis
(‘arnon_c’), various
, the
choices are those, along with Wood’s Y basis (‘wood_y’), Wood’s Z
basis (‘wood_z’), Wall’s basis (‘wall’ or ‘wall_long’), Arnon’s A
basis (‘arnon_a’ or ‘arnon_a_long’), Arnon’s C basis
(‘arnon_c’), various 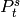 bases (‘pst_ORDER’ for
various values of ORDER), and various commutator bases
(‘comm_ORDER’ or ‘comm_ORDER_long’ for various values of
ORDER).
bases (‘pst_ORDER’ for
various values of ORDER), and various commutator bases
(‘comm_ORDER’ or ‘comm_ORDER_long’ for various values of
ORDER).
See documentation for the function steenrod_algebra_basis for full descriptions of these bases.
To access representations of elements with respect to these different bases, you can either use the basis method for an element, or define a Steenrod algebra with respect to a particular basis and then use that:
sage: c = Sq(2) * Sq(1); c
Sq(0,1) + Sq(3)
sage: c.basis('serre-cartan')
Sq^{2} Sq^{1}
sage: c.basis('milnor')
Sq(0,1) + Sq(3)
sage: adem = SteenrodAlgebra(2, 'serre-cartan')
sage: x = Sq(7,3,1) # top class in the subalgebra A(2)
sage: adem(x)
Sq^{17} Sq^{5} Sq^{1}
sage: SteenrodAlgebra(2, 'pst')(x)
P^{0}_{1} P^{0}_{2} P^{1}_{1} P^{0}_{3} P^{1}_{2} P^{2}_{1}
Multiplication works within bases:
sage: adem = SteenrodAlgebra(2, 'adem')
sage: x = adem.Sq(5)
sage: y = adem.Sq(1)
sage: x * y
Sq^{5} Sq^{1}
When multiplying elements defined with respect to different bases, the result is printed in the basis of the left-hand factor:
sage: milnor = SteenrodAlgebra(2, 'milnor')
sage: xm = milnor.Sq(5)
sage: ym = milnor.Sq(1)
sage: xm * ym
Sq(3,1)
sage: xm * y
Sq(3,1)
sage: x * ym
Sq^{5} Sq^{1}
Several of these bases (‘arnon_a’, ‘wall’, ‘comm’) have alternate,
longer, representations. These provide ways of expressing elements
of the Steenrod algebra in terms of the 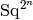 .
.
sage: Sq(6).basis('arnon_a_long')
Sq^{1} Sq^{2} Sq^{1} Sq^{2} + Sq^{2} Sq^{4}
sage: Sq(6).basis('wall_long')
Sq^{2} Sq^{1} Sq^{2} Sq^{1} + Sq^{2} Sq^{4}
sage: SteenrodAlgebra(2,'comm_deg_long')(Sq(6))
s_{1} s_{2} s_{12} + s_{2} s_{4}
INTERNAL DOCUMENTATION:
Here are details on the class SteenrodAlgebraElement (for people who want to delve into or extend the code):
Attributes for a SteenrodAlgebraElement self:
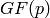 , where
, where
 is the associated prime
is the associated prime
The dictionaries are defined as follows. In the Milnor basis at the
prime 2, for example, since monomials are of the form
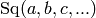 , then monomials are stored as tuples
of integers (a,b,c,...). Thus if
, then monomials are stored as tuples
of integers (a,b,c,...). Thus if
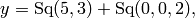
then y._raw['milnor'] is {(0, 0, 2): 1, (5, 3): 1}. (The 1’s following the colons are the coefficients of the monomials associated to the tuples.) Each basis has its own representation as a dictionary; Arnon’s C basis represents basis elements as tuples of integers, just like the Milnor basis and the Serre-Cartan basis, while the other bases represent basis elements as tuples of pairs of integers. From the descriptions of the bases given in the file ‘steenrod_algebra_bases.py’, it should be clear how to associate a tuple of pairs of integers to a basis element. See also the function string_rep.
When the element is initially defined by calling Sq or SteenrodAlgebraElement, typically only the ‘milnor’ dictionary is non-empty, while if the element is defined by the function steenrod_algebra_basis, its dictionary for the given basis is also initialized correctly. For example:
sage: B = steenrod_algebra_basis(6,'adem'); B
(Sq^{6}, Sq^{5} Sq^{1}, Sq^{4} Sq^{2})
sage: x = B[1]; x
Sq^{5} Sq^{1}
sage: x._raw
{'milnor': {(3, 1): 1}, 'serre-cartan': {(5, 1): 1}}
Note that the keys ‘milnor’ and ‘serre-cartan’ (a synonym for ‘adem’) have nonempty associated values.
When any element is converted to another basis (by changing the basis and then printing the element), its dictionary for that basis gets stored, as well:
sage: x.basis('arnona')
X^{0}_{0} X^{1}_{0} X^{1}_{1}
sage: x._raw
{'arnona': {((0, 0), (1, 0), (1, 1)): 1},
'milnor': {(3, 1): 1},
'serre-cartan': {(5, 1): 1}}
Methods for a SteenrodAlgebraElement self:
Most of these are self-explanatory.
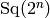 ) may be easy to convert directly. This is
done one basis at a time, and so takes up most of the lines of
code. If the element is not recognizable as being easy to convert,
then the function milnor_convert from the file
‘steenrod_algebra_bases.py’ is called. This does linear algebra: it
computes the Milnor basis and the new basis in the appropriate
dimension, computes the change-of-basis matrix, etc.
) may be easy to convert directly. This is
done one basis at a time, and so takes up most of the lines of
code. If the element is not recognizable as being easy to convert,
then the function milnor_convert from the file
‘steenrod_algebra_bases.py’ is called. This does linear algebra: it
computes the Milnor basis and the new basis in the appropriate
dimension, computes the change-of-basis matrix, etc.REFERENCES:
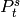 bases for the Steenrod algebra,” J. Pure Appl.
Algebra 125 (1998), no. 1-3, 235-260.
bases for the Steenrod algebra,” J. Pure Appl.
Algebra 125 (1998), no. 1-3, 235-260.Milnor element Sq(a,b,c,...).
INPUT:
OUTPUT: element of the Steenrod algebra
This returns the Milnor basis element ` ext{Sq}(a, b, c, ...)`.
EXAMPLES:
sage: Sq(5)
Sq(5)
sage: Sq(5) + Sq(2,1) + Sq(5) # addition is mod 2:
Sq(2,1)
sage: (Sq(4,3) + Sq(7,2)).degree()
13
Entries must be non-negative integers; otherwise, an error results.
This function is a good way to define elements of the Steenrod algebra.
Bases: sage.structure.element.AlgebraElement
Element of the mod p Steenrod algebra.
At the prime 2, use the function ‘Sq’ to define these, as in ‘w=Sq(4,3,3)’ or ‘z=Sq(1,2)+Sq(4,1)’ or ‘q=Sq(8)*Sq(4) + Sq(12)’.
At odd primes, use the methods ‘P’ and ‘Q’ to define these, as in ‘w=SteenrodAlgebra(3).Q(1,5) * SteenrodAlgebra(3).P(4,3)’.
EXAMPLES:
sage: w = Sq(4,3,3)
sage: w
Sq(4,3,3)
The function ‘Sq’, together with addition, provides an easy way to
define elements when 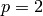 :
:
sage: b = Sq(3) + Sq(0,1)
sage: b
Sq(0,1) + Sq(3)
When  is odd, first define a Steenrod algebra to specify
the prime, and then use the methods ‘P’ and ‘Q’, together with
multiplication and addition:
is odd, first define a Steenrod algebra to specify
the prime, and then use the methods ‘P’ and ‘Q’, together with
multiplication and addition:
sage: A7 = SteenrodAlgebra(7)
sage: u = A7.Q(0,4); u
Q_0 Q_4
sage: v = A7.P(1,2,3); v
P(1,2,3)
sage: u * v
Q_0 Q_4 P(1,2,3)
sage: 10 * u * v
3 Q_0 Q_4 P(1,2,3)
sage: u + v
P(1,2,3) + Q_0 Q_4
The additive order of any nonzero element of the mod p Steenrod algebra is p.
OUTPUT:
EXAMPLES:
sage: z = Sq(4) + Sq(6) + Sq(0)
sage: z.additive_order()
2
sage: (Sq(3) + Sq(3)).additive_order()
1
Serre-Cartan representation of self.
OUTPUT: Serre-Cartan representation of self.
EXAMPLES:
sage: x = Sq(0,1); x
Sq(0,1)
sage: x.serre_cartan()
Sq^{2} Sq^{1} + Sq^{3}
sage: x.adem() # 'adem' is a synonym for 'serre_cartan'
Sq^{2} Sq^{1} + Sq^{3}
Antipode of element.
OUTPUT:
Algorithm: according to a result of Milnor’s, the antipode of
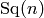 is the sum of all of the Milnor basis
elements in dimension
is the sum of all of the Milnor basis
elements in dimension  . So: convert the element to the
Serre-Cartan basis and use this formula for the antipode of
. So: convert the element to the
Serre-Cartan basis and use this formula for the antipode of
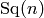 , together with the fact that the antipode is
an antihomomorphism: if we call the antipode
, together with the fact that the antipode is
an antihomomorphism: if we call the antipode  , then
, then
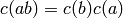 .
.
At odd primes, a similar method is used: the antipode of
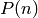 is the sum of the Milnor P basis elements in dimension
is the sum of the Milnor P basis elements in dimension
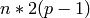 , and the antipode of
, and the antipode of 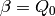 is
is 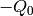 . So
convert to the Serre-Cartan basis, as in the
. So
convert to the Serre-Cartan basis, as in the 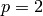 case.
case.
EXAMPLES:
sage: d = Sq(0,0,1); d
Sq(0,0,1)
sage: d.antipode()
Sq(0,0,1)
sage: Sq(4).antipode()
Sq(1,1) + Sq(4)
sage: (Sq(4) * Sq(2)).antipode()
Sq(6)
sage: A3 = SteenrodAlgebra(3)
sage: A3.P(2).antipode()
P(2)
sage: A3.P(2,1).antipode()
2 P(2,1)
Applying the antipode twice returns the original element:
sage: y = Sq(8)*Sq(4)
sage: y == (y.antipode()).antipode()
True
sage: z = A3.P(1,1)
sage: z == (z.antipode()).antipode()
True
sage: w = A3.Q(5)
sage: w == (w.antipode()).antipode()
True
sage: a = SteenrodAlgebra(7).P(55)
sage: a == a.antipode().antipode()
True
TESTS:
sage: all(a.antipode().antipode() == a for a in steenrod_algebra_basis(201, basis='adem', p=5))
True
sage: all(a.antipode().antipode() == a for a in steenrod_algebra_basis(100, basis='milnor', p=3)) # long time (5 seconds)
True
sage: all(a.antipode().antipode() == a for a in steenrod_algebra_basis(30, basis='milnor', p=2)) # long time (15 seconds)
True
sage: all(a.antipode().antipode() == a for a in steenrod_algebra_basis(33, basis='adem', p=2)) # long time (10 seconds)
True
Representation of element with respect to basis.
INPUT:
OUTPUT: Representation of self in given basis
The choices for basis are:
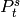 -bases.
-bases.See documentation for the function ‘steenrod_algebra_basis’ for descriptions of the different bases.
EXAMPLES:
sage: c = Sq(2) * Sq(1)
sage: c.basis('milnor')
Sq(0,1) + Sq(3)
sage: c.basis('serre-cartan')
Sq^{2} Sq^{1}
sage: d = Sq(0,0,1)
sage: d.basis('arnonc')
Sq^{2} Sq^{5} + Sq^{4} Sq^{2} Sq^{1} + Sq^{4} Sq^{3} + Sq^{7}
Degree of element.
OUTPUT:
The degree of 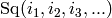 is
is
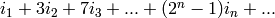 . When
. When
 is odd, the degree of
is odd, the degree of
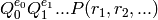 is
is
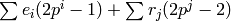 .
.
The degree of a sum is undefined (and this returns ‘None’), unless each summand has the same degree: that is, unless the element is homogeneous.
EXAMPLES:
sage: a = Sq(1,2,1)
sage: a.degree()
14
sage: for a in Sq(3) + Sq(5,1): a.degree()
3
8
sage: (Sq(3) + Sq(5,1)).degree()
Element is not homogeneous.
sage: B = SteenrodAlgebra(3)
sage: x = B.Q(1,4)
sage: y = B.P(1,2,3)
sage: x.degree()
166
sage: y.degree()
192
Excess of element.
OUTPUT:
The excess of 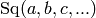 is
is
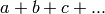 . When
. When  is odd, the excess of
is odd, the excess of
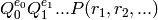 is
is 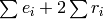 .
.
The excess of a linear combination of Milnor basis elements is the minimum of the excesses of those basis elements.
See [Kra] for the proofs of these assertions.
EXAMPLES:
sage: a = Sq(1,2,3)
sage: a.excess()
6
sage: (Sq(0,0,1) + Sq(4,1) + Sq(7)).excess()
1
sage: [m.excess() for m in (Sq(0,0,1) + Sq(4,1) + Sq(7))]
[1, 5, 7]
sage: [m for m in (Sq(0,0,1) + Sq(4,1) + Sq(7))]
[Sq(0,0,1), Sq(4,1), Sq(7)]
sage: B = SteenrodAlgebra(7)
sage: a = B.Q(1,2,5)
sage: b = B.P(2,2,3)
sage: a.excess()
3
sage: b.excess()
14
sage: (a + b).excess()
3
sage: (a * b).excess()
17
REFERENCES:
return True if element is decomposable, False otherwise.
OUTPUT:
That is, if element is in the square of the augmentation ideal, return True; otherwise, return False.
EXAMPLES:
sage: a = Sq(6)
sage: a.is_decomposable()
True
sage: for i in range(9):
... if not Sq(i).is_decomposable():
... print Sq(i)
Sq(0)
Sq(1)
Sq(2)
Sq(4)
Sq(8)
True if element is not a unit, False otherwise.
EXAMPLES:
sage: z = Sq(4,2) + Sq(7,1) + Sq(3,0,1)
sage: z.is_nilpotent()
True
sage: u = 1 + Sq(3,1)
sage: u == Sq(0) + Sq(3,1)
True
sage: u.is_nilpotent()
False
True if element has a nonzero scalar multiple of P(0) as a summand, False otherwise.
EXAMPLES:
sage: z = Sq(4,2) + Sq(7,1) + Sq(3,0,1)
sage: z.is_unit()
False
sage: u = 1 + Sq(3,1)
sage: u == Sq(0) + Sq(3,1)
True
sage: u.is_unit()
True
sage: A5 = SteenrodAlgebra(5)
sage: v = A5.P(0)
sage: (v + v + v).is_unit()
True
May’s ‘weight’ of element.
OUTPUT:
If we let 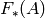 be the May filtration of the Steenrod
algebra, the weight of an element
be the May filtration of the Steenrod
algebra, the weight of an element  is the integer
is the integer
 so that
so that  is in
is in 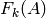 and not in
and not in
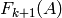 . According to Theorem 2.6 in May’s thesis
[May], the weight of a Milnor basis element is computed as follows:
first, to compute the weight of
. According to Theorem 2.6 in May’s thesis
[May], the weight of a Milnor basis element is computed as follows:
first, to compute the weight of 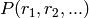 , write
each
, write
each 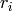 in base
in base  as
as
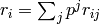 . Then each nonzero binary
digit
. Then each nonzero binary
digit 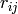 contributes
contributes  to the weight: the
weight is
to the weight: the
weight is 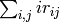 . When
. When  is odd,
the weight of
is odd,
the weight of 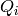 is
is 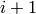 , so the weight of a
product
, so the weight of a
product 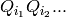 is equal
is equal
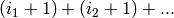 . Then the weight of
. Then the weight of
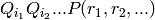 is the
sum of
is the
sum of 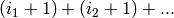 and
and
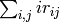 .
.
The weight of a sum of basis elements is the minimum of the weights of the summands.
When 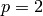 , we compute the weight on Milnor basis elements
by adding up the terms in their ‘height’ - see the method
‘wall_height’ for documentation. (When
, we compute the weight on Milnor basis elements
by adding up the terms in their ‘height’ - see the method
‘wall_height’ for documentation. (When  is odd, the
height of an element is not defined.)
is odd, the
height of an element is not defined.)
EXAMPLES:
sage: Sq(0).may_weight()
0
sage: a = Sq(4)
sage: a.may_weight()
1
sage: b = Sq(4)*Sq(8) + Sq(8)*Sq(4)
sage: b.may_weight()
2
sage: Sq(2,1,5).wall_height()
[2, 3, 2, 1, 1]
sage: Sq(2,1,5).may_weight()
9
sage: A5 = SteenrodAlgebra(5)
sage: a = A5.Q(1,2,4)
sage: b = A5.P(1,2,1)
sage: a.may_weight()
10
sage: b.may_weight()
8
sage: (a * b).may_weight()
18
sage: A5.P(0,0,1).may_weight()
3
REFERENCES:
Milnor representation of self.
OUTPUT: Milnor representation of self.
EXAMPLES:
sage: A = SteenrodAlgebra(2, 'adem')
sage: x = A (Sq(5) * Sq(2) * Sq(1)); x
Sq^{5} Sq^{2} Sq^{1}
sage: x.milnor()
Sq(1,0,1) + Sq(5,1)
Serre-Cartan representation of self.
OUTPUT: Serre-Cartan representation of self.
EXAMPLES:
sage: x = Sq(0,1); x
Sq(0,1)
sage: x.serre_cartan()
Sq^{2} Sq^{1} + Sq^{3}
sage: x.adem() # 'adem' is a synonym for 'serre_cartan'
Sq^{2} Sq^{1} + Sq^{3}
Wall’s ‘height’ of element.
OUTPUT:
The height of an element of the mod 2 Steenrod algebra is a list of
non-negative integers, defined as follows: if the element is a
monomial in the generators 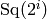 , then the
, then the
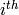 entry in the list is the number of times
entry in the list is the number of times
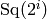 appears. For an arbitrary element, write
it as a sum of such monomials; then its height is the maximum,
ordered right-lexicographically, of the heights of those
monomials.
appears. For an arbitrary element, write
it as a sum of such monomials; then its height is the maximum,
ordered right-lexicographically, of the heights of those
monomials.
When  is odd, the height of an element is not defined.
is odd, the height of an element is not defined.
According to Theorem 3 in [Wall], the height of the Milnor basis
element 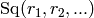 is obtained as
follows: write each
is obtained as
follows: write each 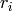 in binary as
in binary as
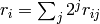 . Then each nonzero binary
digit
. Then each nonzero binary
digit 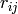 contributes 1 to the
contributes 1 to the 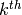 entry in
the height, for
entry in
the height, for 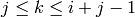 .
.
EXAMPLES:
sage: Sq(0).wall_height()
[]
sage: a = Sq(4)
sage: a.wall_height()
[0, 0, 1]
sage: b = Sq(4)*Sq(8) + Sq(8)*Sq(4)
sage: b.wall_height()
[0, 0, 1, 1]
sage: Sq(0,0,3).wall_height()
[1, 2, 2, 1]
REFERENCES:
Serre-Cartan representation of x.
INPUT:
OUTPUT: Serre-Cartan representation of x
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import serre_cartan
sage: x = Sq(3,2); x
Sq(3,2)
sage: serre_cartan(x)
Sq^{7} Sq^{2}
Serre-Cartan representation of x.
INPUT:
OUTPUT: Serre-Cartan representation of x
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import serre_cartan
sage: x = Sq(3,2); x
Sq(3,2)
sage: serre_cartan(x)
Sq^{7} Sq^{2}
Alternate string representation of element of Arnon’s A basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
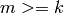
OUTPUT:
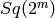 ‘
‘EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import arnonA_long_mono_to_string
sage: arnonA_long_mono_to_string(((1,2),(3,0)))
'Sq^{8} Sq^{4} Sq^{2} Sq^{1}'
sage: arnonA_long_mono_to_string(((1,2),(3,0)),latex=True)
'\text{Sq}^{8} \text{Sq}^{4} \text{Sq}^{2} \text{Sq}^{1}'
The empty tuple represents the unit element Sq(0):
sage: arnonA_long_mono_to_string(())
'Sq(0)'
String representation of element of Arnon’s A basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
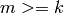
OUTPUT:
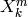 ‘
for each pair (m,k)
‘
for each pair (m,k)EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import arnonA_mono_to_string
sage: arnonA_mono_to_string(((1,2),(3,0)))
'X^{1}_{2} X^{3}_{0}'
sage: arnonA_mono_to_string(((1,2),(3,0)),latex=True)
'X^{1}_{2} X^{3}_{0}'
The empty tuple represents the unit element Sq(0):
sage: arnonA_mono_to_string(())
'Sq(0)'
Return list of digits in the base p expansion of n.
INPUT:
OUTPUT: list of digits in the base p expansion of n
EXAMPLES:
sage: sage.algebras.steenrod_algebra_element.base_p_expansion(10,2)
[0, 1, 0, 1]
sage: sage.algebras.steenrod_algebra_element.base_p_expansion(10,3)
[1, 0, 1]
sage: sage.algebras.steenrod_algebra_element.base_p_expansion(10,5)
[0, 2]
sage: sage.algebras.steenrod_algebra_element.base_p_expansion(10,7)
[3, 1]
sage: sage.algebras.steenrod_algebra_element.base_p_expansion(0,7)
[]
sage: sage.algebras.steenrod_algebra_element.base_p_expansion(100000,13)
[4, 9, 6, 6, 3]
Check that list or tuple consists of non-negative integers, and strip trailing zeroes.
INPUT:
OUTPUT:
If nums contains anything other than a non-negative integer, raise an exception, identifying the right-most problematic entry. Otherwise, return a new list or tuple, obtained from nums by omitting any zeroes from the end.
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import check_and_trim
sage: check_and_trim([3,4,1])
[3, 4, 1]
sage: a=[3,2,1,0,0]
sage: check_and_trim(a)
[3, 2, 1]
sage: a # check_and_trim doesn't affect its input
[3, 2, 1, 0, 0]
sage: check_and_trim([0]*127)
[]
sage: check_and_trim((1,2,3,4,0,0,0)) # works on tuples, too
(1, 2, 3, 4)
Alternate string representation of element of a commutator basis.
Okay in low dimensions, but gets unwieldy as the dimension increases.
INPUT:
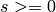 ,
, 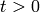
OUTPUT:
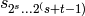 for each pair (s,t)
for each pair (s,t)EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import comm_long_mono_to_string
sage: comm_long_mono_to_string(((1,2),(0,3)))
's_{24} s_{124}'
sage: comm_long_mono_to_string(((1,2),(0,3)),latex=True)
's_{24} s_{124}'
The empty tuple represents the unit element Sq(0):
sage: comm_long_mono_to_string(())
'Sq(0)'
String representation of element of a commutator basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
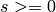 ,
, 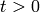
OUTPUT:
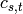 ‘
for each pair (s,t)
‘
for each pair (s,t)EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import comm_mono_to_string
sage: comm_mono_to_string(((1,2),(0,3)))
'c_{1,2} c_{0,3}'
sage: comm_mono_to_string(((1,2),(0,3)),latex=True)
'c_{1,2} c_{0,3}'
The empty tuple represents the unit element Sq(0):
sage: comm_mono_to_string(())
'Sq(0)'
Convert tuple m of non-negative integers to a permutation in one-line form.
INPUT:
OUTPUT:
If m=(3,7,4), then one can view m as representing the permutation of the set 3,4,7 sending 3 to 3, 4 to 7, and 7 to 4. This function converts m to the list [1,3,2], which represents essentially the same permutation, but of the set 1,2,3. This list can then be passed to Permutation, and its signature can be computed.
EXAMPLES:
sage: sage.algebras.steenrod_algebra_element.convert_perm((3,7,4))
[1, 3, 2]
sage: sage.algebras.steenrod_algebra_element.convert_perm((5,0,6,3))
[2, 4, 1, 3]
Degree of x.
INPUT:
OUTPUT:
The degree of 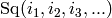 is
is
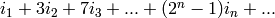 . When
. When
 is odd, the degree of
is odd, the degree of
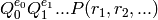 is
is
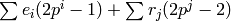 .
.
The degree of a sum is undefined (and this function returns None), unless each summand has the same degree: that is, unless the element is homogeneous.
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import degree
sage: a = Sq(1,2,1)
sage: degree(a)
14
sage: degree(Sq(3) + Sq(5,1))
Element is not homogeneous.
sage: B = SteenrodAlgebra(3)
sage: x = B.Q(1,4)
sage: y = B.P(1,2,3)
sage: degree(x)
166
sage: degree(y)
192
Excess of x.
INPUT:
OUTPUT:
The excess of 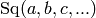 is
is
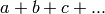 . When
. When  is odd, the excess of
is odd, the excess of
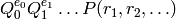 is
is
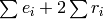 .
.
The excess of a linear combination of Milnor basis elements is the minimum of the excesses of those basis elements.
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import excess
sage: a = Sq(1,2,3)
sage: excess(a)
6
sage: excess(Sq(0,0,1) + Sq(4,1) + Sq(7))
1
sage: [excess(m) for m in (Sq(0,0,1) + Sq(4,1) + Sq(7))]
[1, 5, 7]
sage: B = SteenrodAlgebra(7)
sage: a = B.Q(1,2,5)
sage: b = B.P(2,2,3)
sage: excess(a)
3
sage: excess(b)
14
sage: excess(a + b)
3
sage: excess(a * b)
17
Largest integer k so that 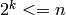
INPUT:
OUTPUT:
This returns the integer  so that
so that 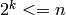 and
and
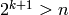 .
.
EXAMPLES:
sage: sage.algebras.steenrod_algebra_element.integer_base_2_log(7)
2
sage: sage.algebras.steenrod_algebra_element.integer_base_2_log(8)
3
sage: sage.algebras.steenrod_algebra_element.integer_base_2_log(9)
3
Milnor representation of x.
INPUT:
OUTPUT: Milnor representation of x
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import milnor
sage: x = Sq(5) * Sq(2) * Sq(1); x.adem()
Sq^{5} Sq^{2} Sq^{1}
sage: milnor(x)
Sq(1,0,1) + Sq(5,1)
String representation of element of the Milnor basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
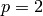 , tuple of non-negative
integers (a,b,c,...); if
, tuple of non-negative
integers (a,b,c,...); if 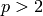 , pair of tuples of
non-negative integers ((e0, e1, e2, ...), (r1, r2, ...))
, pair of tuples of
non-negative integers ((e0, e1, e2, ...), (r1, r2, ...))OUTPUT:
This returns a string like ‘Sq(a,b,c,...)’ when p=2, or a string like ‘Q_e0 Q_e1 Q_e2 ... P(r1, r2, ...)’ when p is odd.
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import milnor_mono_to_string
sage: milnor_mono_to_string((1,2,3,4))
'Sq(1,2,3,4)'
sage: milnor_mono_to_string((1,2,3,4),latex=True)
'\text{Sq}(1,2,3,4)'
sage: milnor_mono_to_string(((1,0), (2,3,1)), p=3)
'Q_1 Q_0 P(2,3,1)'
sage: milnor_mono_to_string(((1,0), (2,3,1)), latex=True, p=3)
'Q_{1} Q_{0} \mathcal{P}(2,3,1)'
The empty tuple represents the unit element Sq(0) (or P(0) at an odd prime):
sage: milnor_mono_to_string(())
'Sq(0)'
sage: milnor_mono_to_string((), p=5)
'P(0)'
The Margolis element 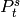 .
.
INPUT:
OUTPUT: element of the Steenrod algebra
This returns the Margolis element 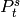 of the mod p
Steenrod algebra: the element equal to
of the mod p
Steenrod algebra: the element equal to 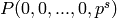 ,
where the
,
where the 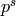 is in position
is in position  .
.
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import pst
sage: pst(3,5)
Sq(0,0,0,0,8)
sage: pst(1,2) + Sq(4)*Sq(2) + Sq(2)*Sq(4)
0
sage: pst(3,5,5)
P(0,0,0,0,125)
sage: pst(3,5,p=5)
P(0,0,0,0,125)
String representation of element of a 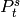 -basis.
-basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
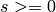 ,
, 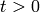
OUTPUT:
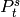 ‘
for each pair (s,t)
‘
for each pair (s,t)EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import pst_mono_to_string
sage: pst_mono_to_string(((1,2),(0,3)))
'P^{1}_{2} P^{0}_{3}'
sage: pst_mono_to_string(((1,2),(0,3)),latex=True)
'P^{1}_{2} P^{0}_{3}'
The empty tuple represents the unit element Sq(0):
sage: pst_mono_to_string(())
'Sq(0)'
Serre-Cartan representation of x.
INPUT:
OUTPUT: Serre-Cartan representation of x
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import serre_cartan
sage: x = Sq(3,2); x
Sq(3,2)
sage: serre_cartan(x)
Sq^{7} Sq^{2}
String representation of element of the Serre-Cartan basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
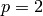 , or tuple (e0, n1, e1, n2, ...) when
, or tuple (e0, n1, e1, n2, ...) when
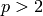 , where each ei is 0 or 1, and each ni is positive
, where each ei is 0 or 1, and each ni is positiveOUTPUT:
This returns a string like ‘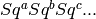 when
when
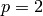 , or a string like
, or a string like
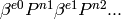 when
when  is odd.
is odd.
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import serre_cartan_mono_to_string
sage: serre_cartan_mono_to_string((1,2,3,4))
'Sq^{1} Sq^{2} Sq^{3} Sq^{4}'
sage: serre_cartan_mono_to_string((1,2,3,4),latex=True)
'\\text{Sq}^{1} \\text{Sq}^{2} \\text{Sq}^{3} \\text{Sq}^{4}'
sage: serre_cartan_mono_to_string((0,5,1,1,0), p=3)
'P^{5} beta P^{1}'
sage: serre_cartan_mono_to_string((0,5,1,1,0), p=3, latex=True)
'\\mathcal{P}^{5} \\beta \\mathcal{P}^{1}'
The empty tuple represents the unit element 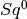 (or
(or
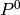 at an odd prime):
at an odd prime):
sage: serre_cartan_mono_to_string(())
'Sq^{0}'
sage: serre_cartan_mono_to_string((), p=7)
'P^{0}'
String representation of element.
INPUT:
OUTPUT:
If latex is True, output a string suitable for LaTeX; otherwise, output a plain string. If sort is True, sort element left lexicographically; otherwise, no sorting is done, and so the order in which the summands are printed may be unpredictable.
EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import string_rep
sage: a = Sq(0,0,2)
sage: A = SteenrodAlgebra(2, 'admissible')
sage: string_rep(A(a))
'Sq^{8} Sq^{4} Sq^{2} + Sq^{9} Sq^{4} Sq^{1} + Sq^{10} Sq^{3} Sq^{1} +
Sq^{10} Sq^{4} + Sq^{11} Sq^{2} Sq^{1} + Sq^{12} Sq^{2} + Sq^{13} Sq^{1}
+ Sq^{14}'
sage: b = Sq(0,2)
sage: string_rep(A(b),latex=True)
'\text{Sq}^{4} \text{Sq}^{2} + \text{Sq}^{5} \text{Sq}^{1} +
\text{Sq}^{6}'
sage: A_wood_z = SteenrodAlgebra(2, 'woodz')
sage: string_rep(A_wood_z(a))
'Sq^{6} Sq^{7} Sq^{1} + Sq^{14} + Sq^{4} Sq^{7} Sq^{3} + Sq^{4} Sq^{7}
Sq^{2} Sq^{1} + Sq^{12} Sq^{2} + Sq^{8} Sq^{6} + Sq^{8} Sq^{4} Sq^{2}'
sage: string_rep(SteenrodAlgebra(2, 'arnonc')(a), sort=False)
'Sq^{4} Sq^{4} Sq^{6} + Sq^{6} Sq^{8} + Sq^{4} Sq^{2} Sq^{8} + Sq^{4}
Sq^{6} Sq^{4} + Sq^{8} Sq^{4} Sq^{2} + Sq^{8} Sq^{6}'
sage: string_rep(SteenrodAlgebra(2, 'arnonc')(a))
'Sq^{4} Sq^{2} Sq^{8} + Sq^{4} Sq^{4} Sq^{6} + Sq^{4} Sq^{6} Sq^{4} +
Sq^{6} Sq^{8} + Sq^{8} Sq^{4} Sq^{2} + Sq^{8} Sq^{6}'
sage: string_rep(SteenrodAlgebra(2, 'pst_llex')(a))
'P^{1}_{3}'
sage: Ac = SteenrodAlgebra(2, 'comm_revz')
sage: string_rep(Ac(a),latex=True,sort=False)
'c_{0,2} c_{0,3} c_{2,1} + c_{1,3} + c_{0,1} c_{1,1} c_{0,3} c_{2,1}'
sage: string_rep(Ac(a),latex=True)
'c_{0,1} c_{1,1} c_{0,3} c_{2,1} + c_{0,2} c_{0,3} c_{2,1} + c_{1,3}'
sage: string_rep(a)
'Sq(0,0,2)'
sage: string_rep(a,latex=True)
'\text{Sq}(0,0,2)'
Some odd primary examples:
sage: A5 = SteenrodAlgebra(5)
sage: a = A5.P(5,1); b = A5.Q(0,1,3)
sage: string_rep(b)
'Q_0 Q_1 Q_3'
sage: string_rep(a, latex=True)
'\mathcal{P}(5,1)'
sage: A5sc = SteenrodAlgebra(5, 'serre-cartan')
sage: string_rep(A5sc(a))
'P^{10} P^{1} + 4 P^{11}'
Alternate string representation of element of Wall’s basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
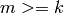
OUTPUT:
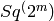 ‘
‘EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import wall_long_mono_to_string
sage: wall_long_mono_to_string(((1,2),(3,0)))
'Sq^{1} Sq^{2} Sq^{4} Sq^{8}'
sage: wall_long_mono_to_string(((1,2),(3,0)),latex=True)
'\text{Sq}^{1} \text{Sq}^{2} \text{Sq}^{4} \text{Sq}^{8}'
The empty tuple represents the unit element Sq(0):
sage: wall_long_mono_to_string(())
'Sq(0)'
String representation of element of Wall’s basis.
This is used by the _repr_ and _latex_ methods.
INPUT:
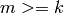
OUTPUT:
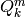 ‘
for each pair (m,k)
‘
for each pair (m,k)EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import wall_mono_to_string
sage: wall_mono_to_string(((1,2),(3,0)))
'Q^{1}_{2} Q^{3}_{0}'
sage: wall_mono_to_string(((1,2),(3,0)),latex=True)
'Q^{1}_{2} Q^{3}_{0}'
The empty tuple represents the unit element Sq(0):
sage: wall_mono_to_string(())
'Sq(0)'
String representation of element of Wood’s Y and Z bases.
This is used by the _repr_ and _latex_ methods.
INPUT:
OUTPUT:
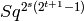 ‘ for each pair (s,t)
‘ for each pair (s,t)EXAMPLES:
sage: from sage.algebras.steenrod_algebra_element import wood_mono_to_string
sage: wood_mono_to_string(((1,2),(3,0)))
'Sq^{14} Sq^{8}'
sage: wood_mono_to_string(((1,2),(3,0)),latex=True)
'\text{Sq}^{14} \text{Sq}^{8}'
The empty tuple represents the unit element Sq(0):
sage: wood_mono_to_string(())
'Sq(0)'